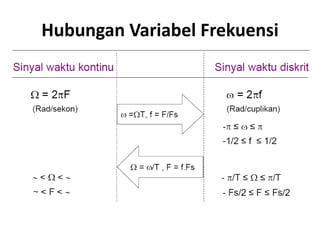
Dokumen tersebut membahas tentang konversi sinyal analog menjadi sinyal digital. Terdapat tiga tahapan utama dalam konversi sinyal analog ke digital yaitu pengambilan sampel, kuantisasi, dan pengkodean ke dalam bentuk bilangan biner. Dokumen tersebut juga menjelaskan pentingnya memenuhi teorema Nyquist agar tidak terjadi aliasing akibat frekuensi sampling yang terlalu rendah.

1. Analog Digital Converter
Simon Patabang
http://spatabang.blogspot.com
Fakultas Teknik
Jurusan Teknik Elektro
Universitas Atma Jaya Makassar

2. Sinyal analog dan sinyal digital
• Sinyal analog adalah sinyal data dalam bentuk
gelombang yang kontinyu, yang membawa
informasi dengan mengubah karakteristik
gelombang.
• Sinyal digital merupakan sinyal data dalam bentuk
pulsa yang dapat mengalami perubahan yang tiba-
tiba dan mempunyai besaran 0 dan 1.

4. Elemen-Elemen Dasar Pengolahan Sinyal Digital
Pemrosesan sinyal digital dapat dilakukan terhadap sinyal
Analog maupun Sinyal Digital. Blok ADC mengubah sinyal
analog menjadi digital sedangkan blok DAC mengubah
sinyal digital menjadi sinyal Analog.

5. Proses Konversi sinyal Analog ke digital
1. Pencuplikan ( Sampling) : konversi sinyal analog ke dalam
sinyal amplitudo kontinyu waktu diskrit.
2. Kuantisasi : konversi masing-masing amplitudo kontinyu
waktu diskrit dari sinyal sampel dikuantisasi dalam level 2B ,
dimana B adalah jumlah bit yang digunakan dalam Analog to
Digital Conversion (ADC).
3. Pengkodean : Setiap sinyal amplitudo diskrit yang
dikuantisasi direprentasikan kedalam suatu barisan bilangan
biner dari masing-masing bit.

6. Teorema Sampling
• Kebanyakan sinyal di alam ini ada dalam bentuk
analog. Untuk memperoleh sinyal diskrit dari sinyal
analog harus dilakukan suatu proses yang disebut
sampling. Secara matematik, proses sampling dapat
dinyatakan oleh persamaan berikut :
Untuk < n <- , n integer (bilangan bulat)
dimana:
X(t) = sinyal analog
X(n) = sinyak diskrit
X(nT) sinyal analog yang disampling setiap perioda Ts

7. dimana :
Ts = waktu sampling
Fs = 1/Ts, frekuensi sampling/detik

8. • Secara umum
agar tidak terjadi aliasing besarnya frekuensi
sampling minimal 2 kali frekuensi informasi. Hal ini
disebut dengan teorema Nyquist

9. • Sinyal Sinusoida analog : xa(t) = A Cos (2Ft + )
• Pencuplikan (sampling) periodik dengan laju Fs=1/T
(cuplikan per sekon ) atau T = 1/F :
Hubungan frekuensi (F) sinyal analog dan frekuensi
(f) untuk sinyal diskrit:
f =F/Fs, ekuivalen :  = T

10. f = Frekuensi relatif atau ternormalisasi
 < F < -
<  < -
Kelemahan sinyal digital:
• Dapat terjadi kehilangan informasi akibat
pembulatan saat kuantisasi dan filtering saat
pembalikan kembali ke sinyal analog.
• Diperlukan waktu proses yang lebih lama
dibandingkan sinyal analog, perlu waktu sampling
dan rekonstruksi ulang.

11. Hubungan Variabel Frekuensi

12. Contoh
• Contoh sampling sinyal analog menjadi sinyal diskrit
menggunakan matlab dengan persamaan x(n) = A
sin(2f nTs)
Sinyal Analog
Sinyal Diskrit

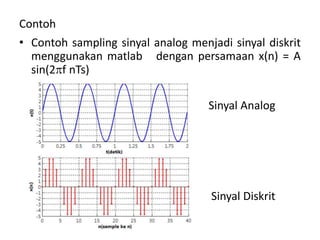
13. Kode Matlab
t = [0:0.0001:2];
A = 5;
f = 2;
xt = A*sin(2*pi*f*t);
subplot(2,2,1);
plot(t,xt,'LineWidth',2);
axis([0 4*(1/f) -A A])
xlabel('t(detik)');
ylabel('x(t)');
box('off');
grid('on');
n = [0:100];
fs = 20;
Ts = 1/fs;
nTs = n*Ts;
xn = A*sin(2*pi*f*nTs);
subplot(2,2,2);
h3 =
stem(n,xn,'.r','LineWidth',2);
axis([0 4*fs/f -A A])
xlabel('n(sample ke n), Ts=1/20
detik');
ylabel('x(n)');
box('off');
grid('on');

14. Output Program

15. TUGAS
Buatlah Sampling sinyal sinusiodal berikut
dengan menggunakan Matlab:
1. x(t) = 3 sin (40t), Ts = 12,5 ms
2. x(t) = 3 sin (90t – 0,25 ), Fs = 0,45 KHz

16. Aliasing
Seperti yang telah disampaikan pada teori sampling,
bahwa agar tidak terjadi aliasing maka Frekuensi
Sampling > 2 x Frekuensi Informasi. Bagaimana
terjadinya Aliasing tersebut dapat dilihat pada contoh
berikut ini:
Misalnya
Jika kedua sinyal tersebut disampling dengan frekuensi
sampling yang sama Fs 40 Hz, tentukanlah x1(n) dan
x2(n).

17. Jawab: Frekuensi :
X1  f=10Hz
X2  f = 50 Hz

18. Frekuensi sampling x1 dan x2 sama, yaitu 5 gelombang
dengan frekuensi Fs = 40Hz
Sampling x1

19. Sampling x2

20. • Sampling sinyal x1 dan x2 menghasilkan output
sinyal digital yang sama, maka terjadi aliasing antara
F1= 10Hz dan F2=50Hz untuk frekuensi sampling
(Fs=40Hz)
• Agar tidak terjadi aliasing, maka diperlukan frekuensi
sampling > 2 x Frekuensi Maksimal dari sinyal-sinyal
tersebut.
• Dari dua sinyal diatas kita ketahui bahwa FMaks
sebesar 50 Hz.
• Sehingga Frekuensi sampling yang dibutuhkan > 2 x
Fmaks misalnya kita gunakan Frekuensi Sampling
sebesar 150 Hz. Perhatikan hasil sampling kedua
sinyal tersebut:

22. Sekian