Praktikum ini bertujuan untuk menganalisis bentuk grafik dan perbandingan tegangan output terhadap variasi frekuensi pada rangkaian RC integral dan diferensial. Percobaan dilakukan dengan manipulasi frekuensi 25 Hz, 50 Hz, dan 100 Hz pada kedua rangkaian. Hasilnya menunjukkan bahwa pada rangkaian integral, tegangan output berkurang seiring kenaikan frekuensi dan periode berkurang. Sedangkan pada rangkaian diferensial, tegangan output

1. Laboratorium Fisika FKIP UNLAM Banjarmasin 1
Abstrak—Praktikum bertujuan {(melihat bentuk
tampilan gambar rangkaian RC integral dan
diferensial), (menganalisis bentuk persamaan Vc(t)
melalui pola grafik yang ditampilkan dan
menghitung perbandingan antara tegangan output)
dan (input terhadap variasi perioda baik pada
rangkaian integral maupun diferensial.)}.
Percobaan dilakukan 2 kali, pada rangkaian
Integral & diferensial RC dengan memanipulasi
frekuensi berturut-turut 25 Hz,50Hz, dan 100 Hz.
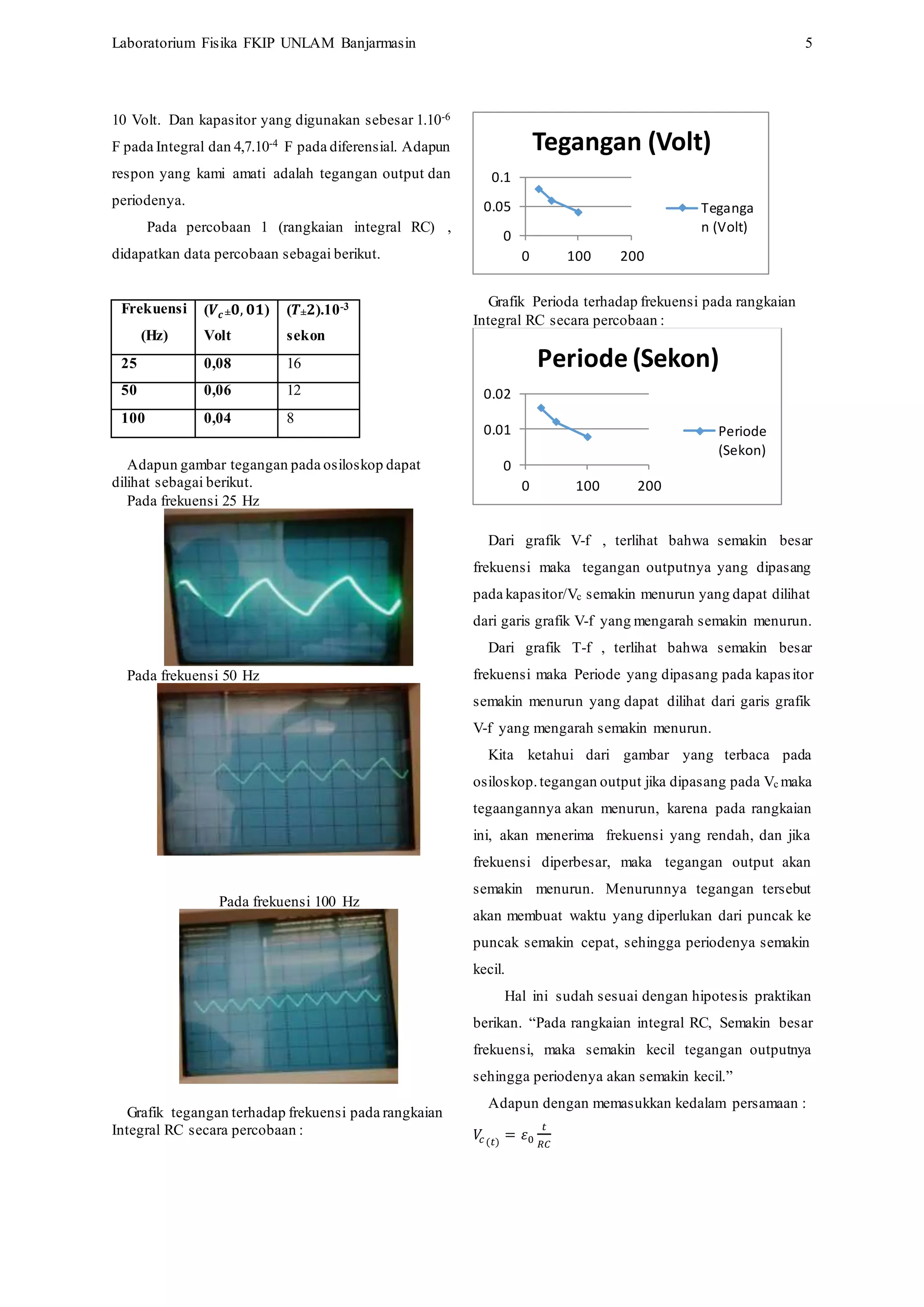
Pada percobaan 1, didapat Voutput berturut-turut
{(0,08± 𝟎, 𝟎𝟏) V, (0,06± 𝟎, 𝟎𝟏) V & (0,04± 𝟎, 𝟎𝟏) V} dan
Peiode {(𝟏𝟔± 𝟐).10-3 sekon, (𝟏𝟐± 𝟐).10-3 sekon &
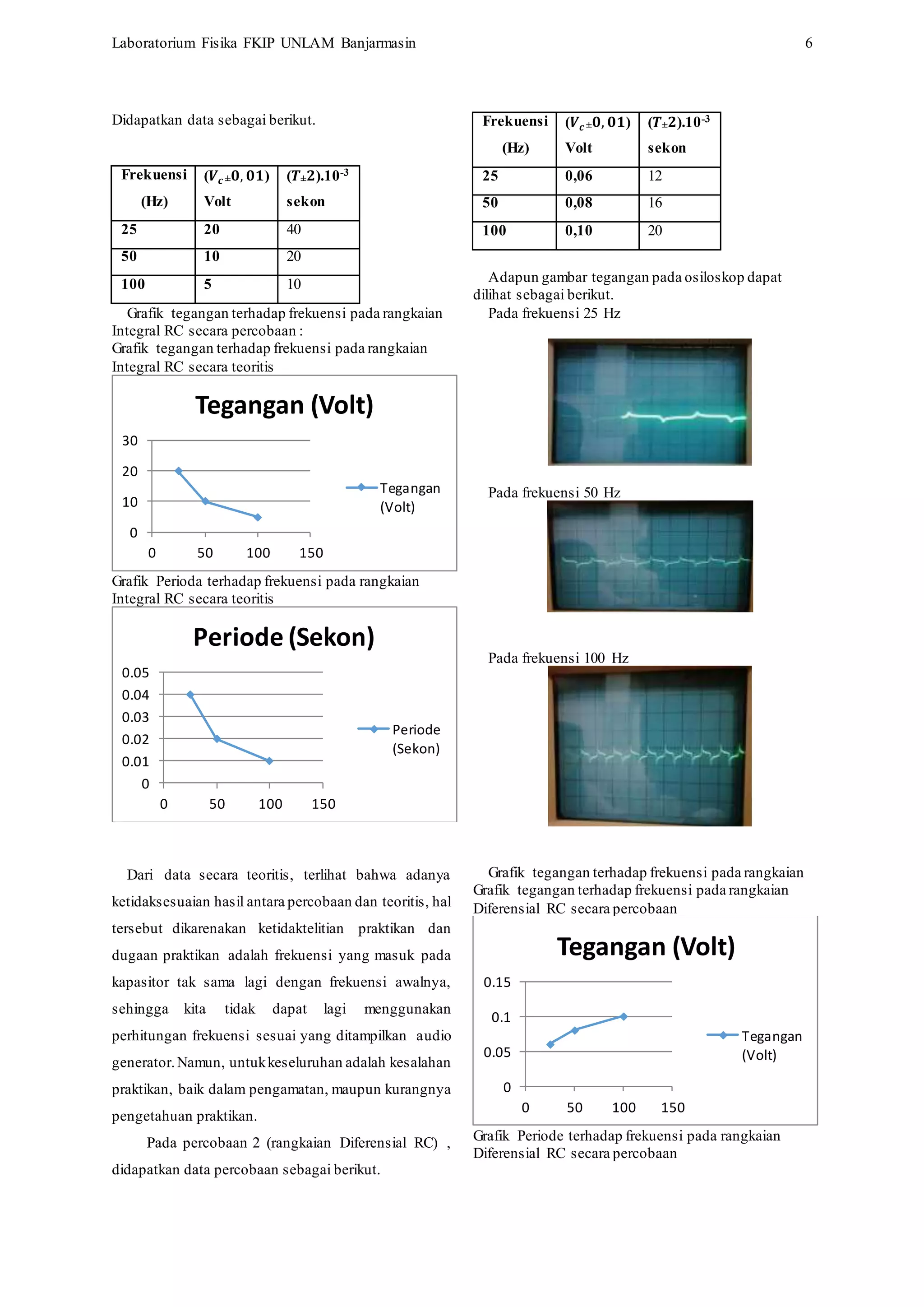
(𝟏𝟔± 𝟐).10-3 sekon}. Percobaan 2, didapat Voutput
berturut-turut {(0,06± 𝟎, 𝟎𝟏) V, (0,08± 𝟎, 𝟎𝟏) V &
(0,10± 𝟎, 𝟎𝟏) V} dan Peiode {(𝟏𝟐± 𝟐).10-3
sekon, (𝟏𝟔± 𝟐).10-3 sekon & (𝟐𝟎± 𝟐).10-3 sekon}.
Percobaan menunjukkan kesesuaian antara
grafik dan hipotesis. Dan menunjukkan
ketidaksesuaian nilai secara teoritis dan grafik
periode secara teoritis
Kata Kunci—Integral,Diferensial,Rangkaian RC
& frekuensi.
PENDAHULUAN
Dalam kehidupan sehari-hari kita tidak pernah lepas
dengan listrik. Salah satu komponen listrik adalah
kapasitor. Kapasitor merupakan komponen pasif.
Ketika kapasitor dihubungkan menjadi rangkaian RC
dengan tegangan AC maka akan memberikan bentuk
luaran yang berbeda-beda pada osiloskop. Pada
praktikum kali ini akan membahas mengenai rangkaian
RC tersebut baik integral/diferensial.
Adapun rmusan masalah sebagai berikut.
“Bagaimanakah perbandingan antara tegangan output
dan tegangan input terhadap variasi perioda input baik
pada rangkaian integral dan diferensial?
Adapun tujuan praktikum adalah untuk melihat
bentuk tampilan gambar rangkaian RC integral dan
diferensial, menganalisis bentuk persamaan Vc(t)
melalui pola grafik yang ditampilkan dan menghitung
perbandingan antara tegangan output dan input
terhadap variasi perioda baik pada rangkaian integral
maupun diferensial.
I.KAJIAN TEORI
Kapasitor/kondensor adalah komponen
elektronika yang dapat menyimpan energi listrik dalam
bentuk muatan listrik selama waktu tertentu atau
komponen elektronika yang berfungsi menampung
muatan listrik yang bersifat sementara agar arus yang
keluar konstan.
Kapasitor dapat didefinisikan sebagai
perbandingan antara muatan dan tegangan.
𝑞 =
𝐶
𝑉
(1)
Berdasarkan nilainya, kapasitor terbagi 2, yaitu
kapasitor tetap dan kapasitor variabel. Berdasarkan
bahan dielektriknya, kapasitor terbagi menjadi
kapasitor ika, kertas, udara, keramik dan elektrolit.
[2]
Rangkaian RC (Resistor-Kapasitor), atau sering
dikenal dengan istilah RC filter atau RC network,
adalah rangkaian listrik yang tersusun dari resistordan
kapasitor. Rangkaian RC orde satu (first order)
RANGKAIAN INTEGRAL & DIFERENSIAL RC
(E-3)
Wahyu Aji Pratama, Fitriani Setiasih, Ichwan Rismayandie, Nanik Lestari, Siva soraya, Syara Suciati, Viky
Fatmawati, asisten praktikum Helda Wahyuni
Prodi Pend.Fisika, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Lambung Mangkurat
Jl. Brigjend H. Hasan Basry, Banjarmasin 70123
e-mail: info@unlam.ac.id

2. Laboratorium Fisika FKIP UNLAM Banjarmasin 2
tersusun dari satu resistor dan satu kapasitor yang
merupakan rangkaian RC paling sederhana.
Rangkaian RC dapat digunakan untuk menyaring
(filter) sinyal dengan cara menahan (block) frekuensi
sinyal tertentu dan meneruskan (pass) sinyal yang
lainnya. Ada 4 macam filter RC, di antaranya: high-
pass filter, low-pass filter, band-pass filter, dan band-
stop filter.
[4]
Dasar pemahaman tentang proses tanggapan
frekuensi ini, maka kita hanya akan mengkaji pada
sifat RC yang bisa meloloskan frekuensirendahdantinggi
dan sebagai alat pengubah (converter) gelombang
persegi-ke-segitiga dan persegi-ke-pulsa dengan,masing-
masing, mengintegrasikan dan mendiferensialkan
gelombang input dan rangkaiannya sendiri masing-
masing disebut rangkaian integrator dan rangkaian
diferensiator orde 1.
Untukpengintegralan RC,sinyalkeluaran rangkaian
merupakan integral dari sinyal masukan. untuk
pendiferensialan RC, sinyal keluaran rangkaian
merupakan diferensial dari sinyal masukan.
[1]
Analisis Matematis Rangkaian Integral dan
Diferensial
Pada percobaan pertama, kita telah mengenal suatu
persamaan kapasitor yang mengikuti fungsi
eksponensialyaitu :
Vc(t) = εo (1-e-t/RC) (2)
Jika dianalisis persamaan ini maka ada beberapa
kesesuaian antara tampilan isyarat output dengan
persamaan diatas. Untuk itu contoh-contoh dibawah
ini akan memberikan gambaran hal tersebut yakni:
1. Rangkaian Integral
Misalkan kita memiliki suatu rangkaian integral
RC dengan nilai RC=T detik (tetapan waktu-), yang
bermakna fisis bahwa waktu minimal yang
dibutuhkan kapasitor untukmengisi penuh kapasitor.
Misalkan T/2<<RC maka, dari persamaan (2)
dapat dituliskan seperti berikut:
Vc(t) = εo (1- e-t/RC
)untukt =
(3)
Sebaliknya jika RC >>T/2, maka secara teori
memperlihatkan bahwa sebelum kapasitor penuh
dengan muatan, tegangan input sudah berubah tanda,
sehingga tegangan kapasitortidak akan sama dengan
tegangan input. Model persamaan matematis kapasitor
demikian adalah:
Vc(t) = εo (1-e-t/RC
) (4)
Karena RC>>T, maka dengan menggunakan
deret taylor untuk ekspansit/RC diperoleh:
Vc(t) = εo
R C
t
; untuk 0 ≤ t≤ T/2 (5)
2. Rangkaian Diferensial RC
Untuk rangkaian diferensial RC yang menjadi
output diambil dari resistoryang terpasang.Sehingga
persamaan tegangannya untuk RC<<T/2 dinyatakan
oleh :
Vr (t) = εo –Vc (t) = εo.e-t/RC
(6)
Dimana untukt = T/2 harga Vr(t) = 0.
Sedangkan untuk RC>> T/2, maka persamaan
(5) dinyatakan oleh persamaan:
Vr (t) = εo (1 -
R C
t
) (7)
Dimana perbandingan:
(8)
[5]
Perhatikan Gambar berikut.
0 ≤ t ≤ T/2
T/2 ≤ t ≤0
εo – Vr(t) t
εo RC
=

3. Laboratorium Fisika FKIP UNLAM Banjarmasin 3
Gambar 1. Grafik pengintegralan RC
Seperti ditunjukkan pada gambar 1 jika tetapan
waktu 𝜏 << T, kapasitor C terisi penuh dalam waktu
T/2. Akan tetapi jika 𝜏 >> T, maka sebelum kapasitor
terisi penuh, tegangan Vs sudah berbalik menjadi
negatif. Akibatnya kapasitor segera dikosongkan.
Belum lagi terisi penuh, Vs sudah berubah tanda lagi.
Akibatnya isyarat kéluaran akan berupa suatu tegangan
yang berbentuk gelombang segtiga. Untuk 𝜏>> RC,
bentuk jsyarat keluaran seperti integral isyarat
masukan. untuk 𝜏 =R>> T pada waktu Vs =+ V p,
kerniringan Vo (t) positif, dan pada waktu Vs=-V p,
kemiringan Vo (t) negatif. Ini disebut rangkaian
pengintegralan RC.
Gambar 2. Grafik pendiferensialan RC
Rangkaian RC akan berlaku sebagai suatu
pendiferensial jika dipasang seperti pada gambar 2
Untuk 𝜏=RC<< T, isyarat keluaran akan seperti
diferensial dari isyarat masukan. jika 𝜏=RC>> T,
bentukisyaratmirip dengan isyarat masukan, akan
tetapi puncaknya miring. Jika RC<<T,isyarat
berbentuk denyut dengan tegangan puncak 2 V.
[3]
IV. METODE PERCOBAAN
Alat dan Bahan
Alat dan bahan yang dipergunakan antara lain 1
buah komponen kapasitor dan resistor, 1 buah audio
generator, 1 buah Osiloskop dan 3 buah kabel
penghubung.
Hipotesis
“Pada rangkaian integral RC, Semakin besar
frekuensi, maka semakin kecil tegangan outputnya
sehingga periodenya akan semakin kecil. Pada
rangkaian Diferensial RC, semakin besar frekuensi,
semakin besar pula tegangan outputnya sehingga
periodenya akan semakin membesar. ”
Identifikasi dan Definisi overasional Variabel.
Pada percobaan ini, kami memanipulasi frekuensi
dan jenis rangkaian. Kami mengamati respon pada
periode dan tegangan output dan variabel yang dijaga
tetap/dikontrol yaitu kapasitor, resistor, tegangan input
(Vs), osiloskop, audio generator dan kabel
penghubung.
Pada variabel manipulasi, kami memanipulasi jenis
rangkaian menjadi 2, yaitu rangkaian integral yang
mana tegangan outputnya dipasangpada kapasitor,dan
rangkaian diferensial yang tegangan outputnya
dipasang pada resistor. Pada variabel respon, kami
mengamati besar periode dalam satuan sekon dan
tegangan output dalam satuan volt yang terbaca pada
osiloskop. Adpaun variabel kontrol, kami menjaga
tetap kapasitor yang digunakan sebesar 1.10-6 F pada
Integral dan 4,7.10-4 F pada diferensial. Resistor yang
digunakan sebesar 104 Ω , tegangan input yang
digunakan sebesar 10 Volt dan mennggunakan
osiloskop, audio generator yang sama pada setiap
percobaan, serta kabel penghubung yang dugunakan
sebanyak 3 buah.
Langkah Kerja
Rangkaian Integral RC.
Pertama-tama membentuk rangkaian seperti gambar
3, mencatat dan mengukur nilai kapasitor, resistor dan

4. Laboratorium Fisika FKIP UNLAM Banjarmasin 4
tegangan puncak Vp audio generator untuk tegangan
persegidan mempelajari kalibrasi time/div dan volt/div
pada osiloskop. Setelah itu untuk tegangan output
mengkalibrasi osiloskop. Kemudian memutar
tombol/pemutar frekusnsi pada penunjukan 25 Hz.
Mengukur tegangan puncak yang tampak pada layar
monitor dan sekaligus gambar. Melakukan percobaan
yang sama pada frekuensi 50 Hz dan 100 Hz. Mencatat
hasil pada tabel pengamatan.
Rangkaian Diferensial RC.
Pertama-tama membentuk rangkaian seperti gambar
3, mencatat dan mengukur nilai kapasitor, resistor dan
tegangan puncak Vp audio generator untuk tegangan
persegidan mempelajari kalibrasi time/div dan volt/div
pada osiloskop. Setelah itu untuk tegangan output
mengkalibrasi osiloskop. Kemudian memutar
tombol/pemutar frekusnsi pada penunjukan 25 Hz.
Mengukur tegangan puncak yang tampak pada layar
monitor dan sekaligus gambar. Melakukan percobaan
yang sama pada frekuensi 50 Hz dan 100 Hz. Mencatat
hasil pada tabel pengamatan.
Tabel Pengamatan
Tabel 1. Tabel Rangkaian Integral RC.
Frekuensi
(Hz)
(𝑽𝒄 ± 𝟎, 𝟎𝟏)
Volt
(𝑻± 𝟐).10-3
sekon
25
50
100
Tabel 2. Tabel Rangkaian Diferensial RC.
Frekuensi
(Hz)
(𝑽𝒄 ± 𝟎, 𝟎𝟏)
Volt
(𝑻± 𝟐).10-3
sekon
25
50
100
TEKNIK ANALISIS
1. Rangkaian Integral RC
𝑉𝑐 (𝑡)
= 𝜀0
𝑡
𝑅𝐶
2. Rangkaian Diferensial RC
𝑉𝑟 = 𝜀0(1 −
𝑡
𝑅𝐶
)
PEMBAHASAN
Pada praktikum kali ini bertujuan untuk melihat
bentuk tampilan gambar rangkaian RC integral dan
diferensial, menganalisis bentuk persamaan Vc(t)
melalui pola grafik yang ditampilkan dan menghitung
perbandingan antara tegangan output dan input
terhadap variasi perioda baik pada rangkaian integral
maupun diferensial.
Kami melakukan percobaan dengan 2 jenis
rangkaian yang berbeda. Percobaan pertama
menggunakan rangkaian diferensial RC dan percobaan
pertama menggunakan rangkaian diferensial RC. Pada
kedua percobaan kami memanipulasi frekuensi sebesar
25 Hz, 50 Hz, dan 100 Hz. Kami menggunakan nilai
resistor sebesar 104 Ω. Tegangan sumber (Vs) sebesar
Gambar 3. Rangkaian Integral
RC
Vo
R
Cεo

5. Laboratorium Fisika FKIP UNLAM Banjarmasin 5
10 Volt. Dan kapasitor yang digunakan sebesar 1.10-6
F pada Integral dan 4,7.10-4 F pada diferensial. Adapun
respon yang kami amati adalah tegangan output dan
periodenya.
Pada percobaan 1 (rangkaian integral RC) ,
didapatkan data percobaan sebagai berikut.
Frekuensi
(Hz)
(𝑽𝒄 ± 𝟎, 𝟎𝟏)
Volt
(𝑻± 𝟐).10-3
sekon
25 0,08 16
50 0,06 12
100 0,04 8
Adapun gambar tegangan pada osiloskop dapat
dilihat sebagai berikut.
Pada frekuensi 25 Hz
Pada frekuensi 50 Hz
Pada frekuensi 100 Hz
Grafik tegangan terhadap frekuensi pada rangkaian
Integral RC secara percobaan :
Grafik Perioda terhadap frekuensi pada rangkaian
Integral RC secara percobaan :
Dari grafik V-f , terlihat bahwa semakin besar
frekuensi maka tegangan outputnya yang dipasang
pada kapasitor/Vc semakin menurun yang dapat dilihat
dari garis grafik V-f yang mengarah semakin menurun.
Dari grafik T-f , terlihat bahwa semakin besar
frekuensi maka Periode yang dipasang pada kapasitor
semakin menurun yang dapat dilihat dari garis grafik
V-f yang mengarah semakin menurun.
Kita ketahui dari gambar yang terbaca pada
osiloskop.tegangan output jika dipasang pada Vc maka
tegaangannya akan menurun, karena pada rangkaian
ini, akan menerima frekuensi yang rendah, dan jika
frekuensi diperbesar, maka tegangan output akan
semakin menurun. Menurunnya tegangan tersebut
akan membuat waktu yang diperlukan dari puncak ke
puncak semakin cepat, sehingga periodenya semakin
kecil.
Hal ini sudah sesuai dengan hipotesis praktikan
berikan. “Pada rangkaian integral RC, Semakin besar
frekuensi, maka semakin kecil tegangan outputnya
sehingga periodenya akan semakin kecil.”
Adapun dengan memasukkan kedalam persamaan :
𝑉𝑐 (𝑡)
= 𝜀0
𝑡
𝑅𝐶
0
0.05
0.1
0 100 200
Tegangan (Volt)
Teganga
n (Volt)
0
0.01
0.02
0 100 200
Periode (Sekon)
Periode
(Sekon)

6. Laboratorium Fisika FKIP UNLAM Banjarmasin 6
Didapatkan data sebagai berikut.
Frekuensi
(Hz)
(𝑽𝒄 ± 𝟎, 𝟎𝟏)
Volt
(𝑻± 𝟐).10-3
sekon
25 20 40
50 10 20
100 5 10
Grafik tegangan terhadap frekuensi pada rangkaian
Integral RC secara percobaan :
Grafik tegangan terhadap frekuensi pada rangkaian
Integral RC secara teoritis
Grafik Perioda terhadap frekuensi pada rangkaian
Integral RC secara teoritis
Dari data secara teoritis, terlihat bahwa adanya
ketidaksesuaian hasil antara percobaan dan teoritis, hal
tersebut dikarenakan ketidaktelitian praktikan dan
dugaan praktikan adalah frekuensi yang masuk pada
kapasitor tak sama lagi dengan frekuensi awalnya,
sehingga kita tidak dapat lagi menggunakan
perhitungan frekuensi sesuai yang ditampilkan audio
generator.Namun, untukkeseluruhan adalah kesalahan
praktikan, baik dalam pengamatan, maupun kurangnya
pengetahuan praktikan.
Pada percobaan 2 (rangkaian Diferensial RC) ,
didapatkan data percobaan sebagai berikut.
Frekuensi
(Hz)
(𝑽𝒄 ± 𝟎, 𝟎𝟏)
Volt
(𝑻± 𝟐).10-3
sekon
25 0,06 12
50 0,08 16
100 0,10 20
Adapun gambar tegangan pada osiloskop dapat
dilihat sebagai berikut.
Pada frekuensi 25 Hz
Pada frekuensi 50 Hz
Pada frekuensi 100 Hz
Grafik tegangan terhadap frekuensi pada rangkaian
Grafik tegangan terhadap frekuensi pada rangkaian
Diferensial RC secara percobaan
Grafik Periode terhadap frekuensi pada rangkaian
Diferensial RC secara percobaan
0
10
20
30
0 50 100 150
Tegangan (Volt)
Tegangan
(Volt)
0
0.01
0.02
0.03
0.04
0.05
0 50 100 150
Periode (Sekon)
Periode
(Sekon)
0
0.05
0.1
0.15
0 50 100 150
Tegangan (Volt)
Tegangan
(Volt)

7. Laboratorium Fisika FKIP UNLAM Banjarmasin 7
Dari grafik V-f , terlihat bahwa semakin besar
frekuensi maka tegangan outputnya yang dipasang
pada kapasitor/VR semakin membesar yang dapat
dilihat dari garis grafik V-f yang mengarah semakin ke
atas.
Dari grafik T-f , terlihat bahwa semakin besar
frekuensi maka Periode yang dipasang pada kapasitor
semakin menaik juga dan dapat dilihat dari garis grafik
V-f yang mengarah semakin menurun.
Kita ketahui dari gambar yang terbaca pada
osiloskop.tegangan output jika dipasang pada VR maka
tegangannya akan menaik, karena pada rangkaian ini,
ketika tegangan outputnya dipasang pada resistor,
rangkaian akan menerima frekuensi yang tinggi, dan
jika frekuensi diperbesar, maka tegangan output akan
semakin menaik. Menaiknya tegangan tersebut akan
membuat waktu yang diperlukan dari puncak ke
puncak semakin lama, sehingga periodenya semakin
besar.
Hal ini sudah sesuai dengan hipotesis praktikan
berikan. “Pada rangkaian Diferensial RC, semakin
besar frekuensi, semakin besar pula tegangan
outputnya sehingga periodenya akan semakin
membesar.”
Adapun dengan memasukkan kedalam persamaan :
𝑉𝑟 = 𝜀0(1 −
𝑡
𝑅𝐶
)
Didapatkan data sebagai berikut.
Frekuensi
(Hz)
(𝑽𝒄 ± 𝟎, 𝟎𝟏)
Volt
(𝑻± 𝟐).10-3
sekon
25 9,957 40
50 9,98 20
100 9,99 10
Grafik tegangan terhadap frekuensi pada rangkaian
Integral RC secara percobaan :
Grafik tegangan terhadap frekuensi pada rangkaian
Diferensial RC secara teoritis :
Grafik Periode terhadap frekuensi pada rangkaian
Diferensial RC secara teoritis :
Dari data secara teoritis, terlihat bahwa adanya
ketidaksesuaian hasil antara percobaan dan teoritis, hal
tersebut dikarenakan ketidaktelitian praktikan.
Seharusnya nilai tegangan ketika tegangan keluaran
dipasang pada resistorakan mendekati nilai Vs seperti
yang ditampilkan dari data perhitungan teoritis.
Kemudian, ketidaksesuaian juga terdapat pada periode,
periode secara percobaan semakin menaik/membesar
dan periode pada teoritis semakin mengecil. Menuurut
praktikan, karena tegangan semakin besar, maka
semakin besar pula periodanya, bukan semakin
mengecil. Jadi menurut saya perhitungan secara teoritis
kurang tepat, karena kita ketahui, pada saatu tegangan
keluaran di ubah dari kapasitor ke resistor, maka
seharusnya periodenya juga berubah. Namun pada
perhitungan teoritis, periode pada integral dan periode
0
0.01
0.02
0.03
0 50 100 150
Periode (Sekon)
Periode
(Sekon)
9.95
9.96
9.97
9.98
9.99
10
0 50 100 150
Tegangan (Volt)
Tegangan
(Volt)
0
0.02
0.04
0.06
0 50 100 150
Periode (Sekon)
Periode
(Sekon)

8. Laboratorium Fisika FKIP UNLAM Banjarmasin 8
secara diferensial sama, jadi menurut saya
perhitungannya kurang tepat.
Untuk keseluruhan, dengan membandingkan
tegangan output baik itu integral maupun diferensial
memperoleh nilai yang berbeda-beda,bahkan jauh dari
batas toleransi, hal ini dikarenakan ketidaktelitian
praktikan namun untuk grafik, baim percobaan dan
teoritis memperoleh gambar grafik yang hampir
semuanya sama, namun periode antara diferensial
antara percobaan dan teoritidak sama karena kesalahan
praktikan dalam perhitungan.
SIMPULAN
Pada percobaan kali ini, disumpulkan bahwa pada
rangkaian diferensial RC, semakin besar frekuensi
yang diberikan, maka semakin kecil tegangan
outputnya yang membuat periodenya juga semakin
mengecil. Sedangkan pada rangkaian Integral RC,
semakin besar frekuensi yang diberikan, semakin
membesar pula tegangan outputnya yang membuat
periodenya juga semakin membesar.
Berdasarkan praktikum didapatkan perbandingan
antara tegangan output yang berbeda antara percobaan
dan teoritis. Hal ini dikarenakan ketidaktelitian
praktikan dalam pengamatan secara percobaan,namun
untuk grafik tegangan terhadap frekuensinya baik
ragkaian integral dan diferensial secara percobaan dan
teoritis menunjukkan gambar grafik yang sesuai.
UCAPAN TERIMA KASIH
Penulis mengucapkan rasa syukur kepada Allah
SWT karena berkat rahmatNya penulis dapat
menyelesaikan laporan ini dengan lancar. Penulis juga
mengucapkan terimakasih kepada Ibu Misbah, M.Pd
selaku dosen pembimbing. Penulis juga mengucapkan
terimakasih kepada Helda Wahyuni selaku asisten
praktikum selama pengambilan data dan
pembimbingan pembuatan laporan. Serta tidak lupa
ucapan terimakasih ditujukan kepada kedua orang tua
yang selalu mendukung dan mendoakan. Terakhir
untuk teman-teman di kelompok yang telah membantu
banyak hal dalam menyelesaikan laporan ini.
DAFTAR PUSTAKA
[1] Maulana,Andi Ikhsan.“Karakteristik Dioda”,
diakses 7 November 2015. http://www.ilmusemes
ta.com/2014/05/laporan-elektronika-rangkaian-
penapis-rc.html?m=0.
[2] Misbah. 2015. Handout Elektronika daasar.
Banjarmasin : Unlam.
[3] Sutrisno. 1986. Elektronika teori &
penerapannya. Bandung: ITB.
[4] Syaiful.“Jurnal Rangkaian RC dan RL”, diakses 7
November2015. http://semutuyet.blogspot.com/
2011/11/elektronika-1-modul-5-rangkaian-rc-
dan.html.
[5] Tim Dosen Elektronika Dasar.2015.Penuntun
praktikum elektronika dasar 1.Banjarmasin :
Unlam