Downloaded 1,553 times
Uploaded bySaikrishna Tanguturu
Computer Networks - Error Detection & Error Correction
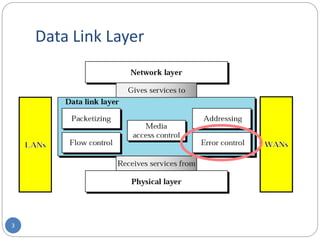
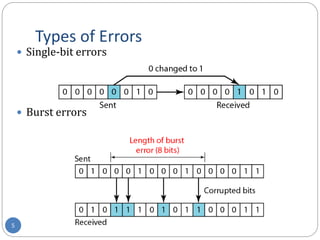
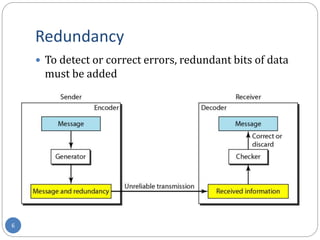
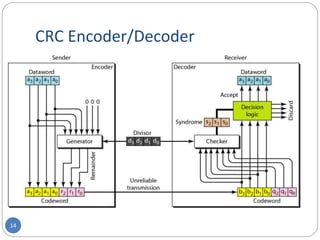
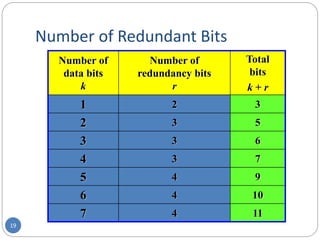
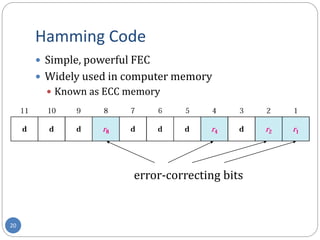
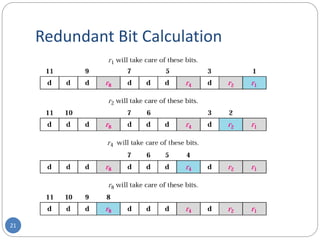
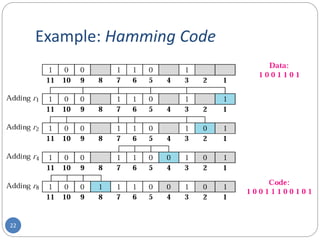
This document provides information about error detection and correction techniques used in computer networks. It discusses different types of errors that can occur like single-bit and burst errors. It explains that redundancy is needed to detect or correct errors by adding extra bits. Detection techniques discussed include parity checks, checksumming, and cyclic redundancy checks. Parity checks can only detect odd number of errors. Cyclic redundancy checks use polynomial arithmetic to generate a checksum. Forward error correction allows detection and correction of errors by adding redundant bits to distinguish different error possibilities. Hamming code is an example of an error correcting code that can detect and correct single bit errors.
More Related Content
Similar to Computer Networks - Error Detection & Error Correction
Computer Networks - Error Detection & Error Correction
- 1. Error Detection &Error Correction Computer Networks
- 2. Team Members Group-I AssignmentTopic : Error Detection & Error Correction Group's representative: TANGUTURU SAI KRISHNA S.No. BITS ID NAME Official Email ID Personal Email ID 1 2011HW69898 TANGUTURU SAI KRISHNA saikrishna.tanguturu@wipro.com sai.tsk2008@gmail.com 2 2011HW69900 RAYAPU MOSES rayapu.moses@wipro.com stalinkvd001@gmail.com 3 2011HW69932 SHENBAGAMOORTHY A shenbagamoorthy.a83@wipro.com moorthy2626@gmail.com 4 2011HW69913 ANURUPA K C anurupa.c85@wipro.com anu.rupa30@gmail.com 5 2011HW69909 ARUNJUNAISELVAM P arunjunaiselvam.p95@wipro.com arunjunai.carrer@gmail.com 6 2011HW69569 PRANOB JYOTI KALITA pranob.kalita@wipro.com pranob.kalita90@gmail.com 7 2011HW69893 TINNALURI V N PRASANTH prasanth.tinnaluri@wipro.com naga.prasanth985@gmail.com 8 2011HW69904 KONDALA SUMATHI sumathi.kondala@wipro.com sumathi.kondala@gmail.com 9 2011HW69896 DASIKA KRISHNA dasika.krishna@wipro.com dasikakrishnas@gmail.com 10 2011HW69907 SHEIK SANAVULLA sheik.sanavulla@wipro.com sanavulla.sms@gmail.com 11 2011HW70163 K ASWINI PRIYANKA kamma.priyanka@wipro.com ashupriya.priyanka6@gmail.com 12 2011HW70828 BODDU MADHAVI REDDY boddu.reddy@wipro.com mreddy786@gmail.com
- 3.
- 4. Definition of Error Networks must be able to transform data from once device to another with complete accuracy. While the transmission data can be corrupted, for reliable communication errors must be detected and corrected.
- 5. 5 Types of Errors Single-bit errors Burst errors
- 6. 6 Redundancy To detector correct errors, redundant bits of data must be added
- 7. Detection/Correction Techniques ParityChecks Checksumming methods Cyclic redundancy checks
- 8. Parity Checks Parity Bit(PB) One additional bit per character Even parity Odd Parity
- 9. How many biterrors can PB detect ? 10001110 --- 10101110 => error ! 10001110 --- 10100110 => No error detected !!! Conclusion – 1 PB can only detect an odd number of errors !
- 10. Single Bit ErrorCorrection Parity for each character(byte=line) + parity for each column (set of data bytes sent)
- 11. Example - SingleBit Error Correction Hamming - Correctable single bit error
- 12. 12 Cyclic Redundancy Checksum(CRC) •CRC error detection method treats packet of data to be transmitted as a large polynomial •Transmitter •Using polynomial arithmetic, divides polynomial by a given generating polynomial •Quotient is discarded •Remainder is “attached” to the end of message
- 13. 13 Cyclic Redundancy Checksum (continued) •Message(with the remainder) is transmitted to the receiver •Receiver divides the message and remainder by same generating polynomial •If a remainder not equal to zero results error during transmission •If a remainder of zero results error during transmission
- 14.
- 15. CRC - Example Frame– 1101011011 G(x)=x4+x+1 Transmitted frame: 11010110110000 – 00000000001110 ---------------------- 11010110111110
- 16. Checksums • Achecksum “adds” together “chunks” of data – The “add” operation may not be normal integer addition – The chunk size is typically 8, 16, or 32 bits • We’ll discuss: – Integer addition “checksum” – One’s complement “checksum” – Fletcher Checksum – Adler Checksum – ATN Checksum (AN/466)
- 17. 17 Error Correction Twomethods Retransmission after detecting error Forward error correction (FEC)
- 18. 18 Forward Error Correction Consider only a single-bit error in k bits of data k possibilities for an error One possibility for no error #possibilities = k + 1 Add r redundant bits to distinguish these possibilities; we need 2r k+1 But the r bits are also transmitted along with data; hence 2r k+r+1
- 19. 19 Number of RedundantBits Number of data bits k Number of redundancy bits r Total bits k + r 1 2 3 2 3 5 3 3 6 4 3 7 5 4 9 6 4 10 7 4 11
- 20. 20 Hamming Code Simple,powerful FEC Widely used in computer memory Known as ECC memory error-correcting bits
- 21.
- 22.
- 23.