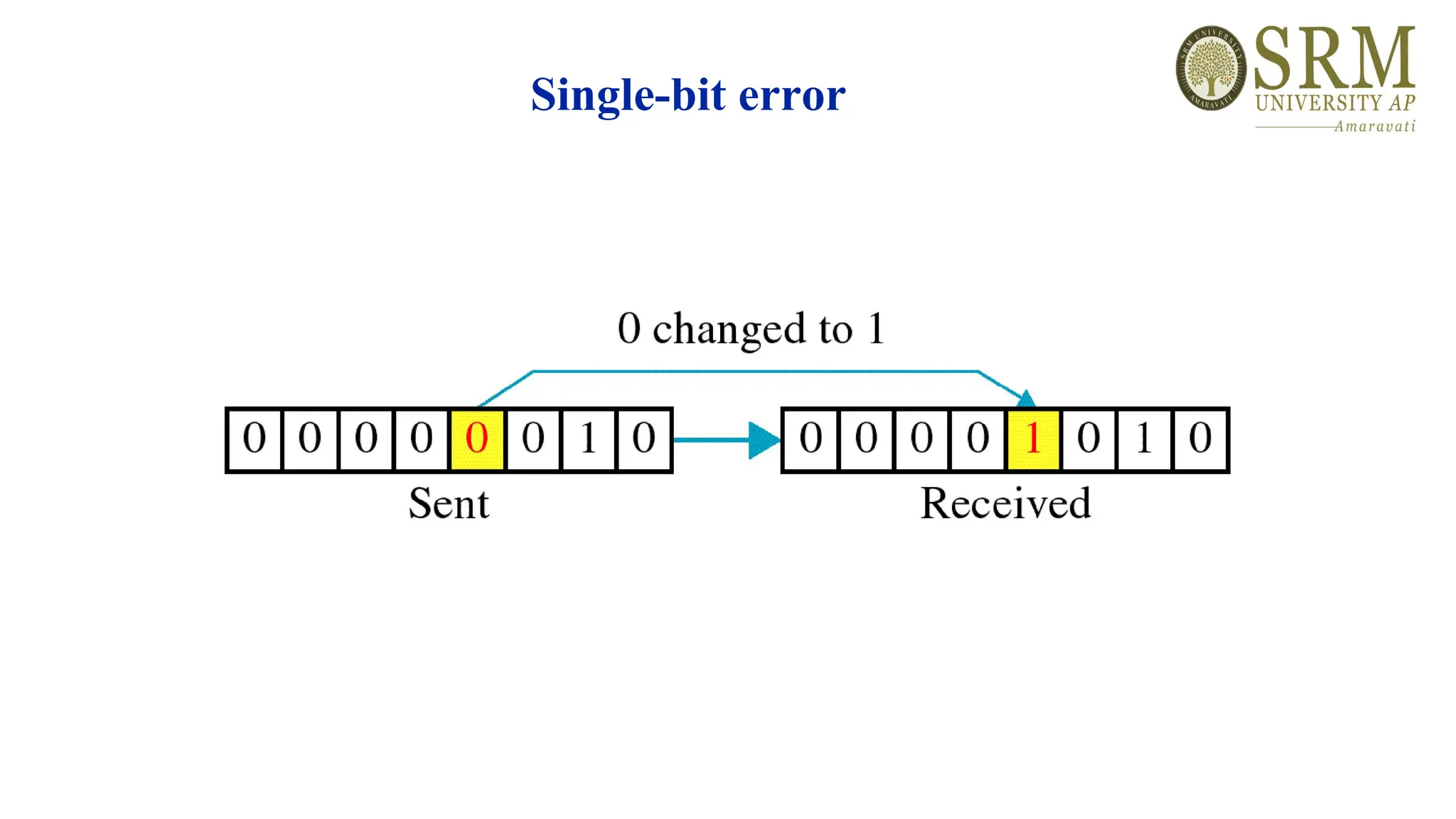
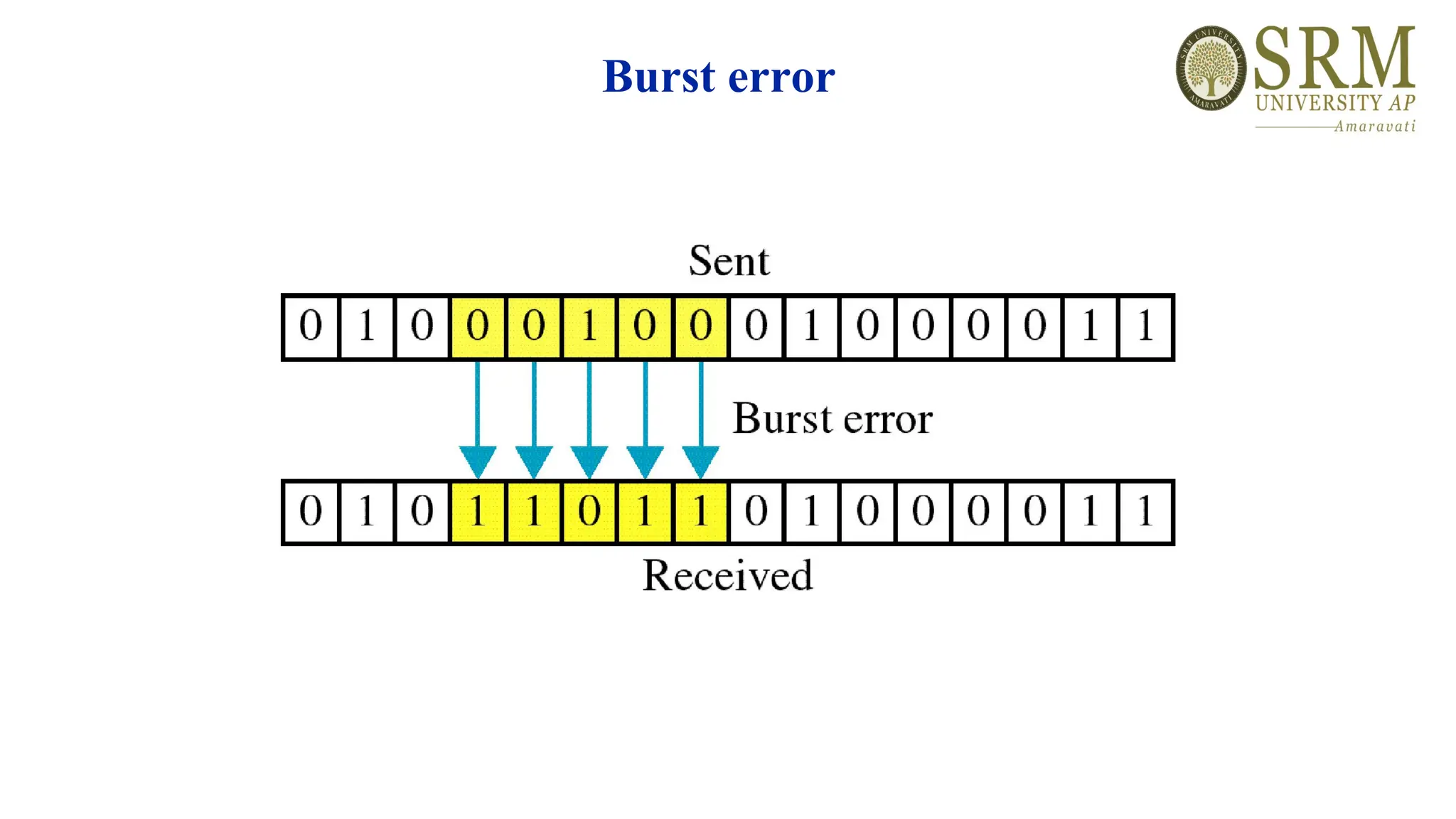
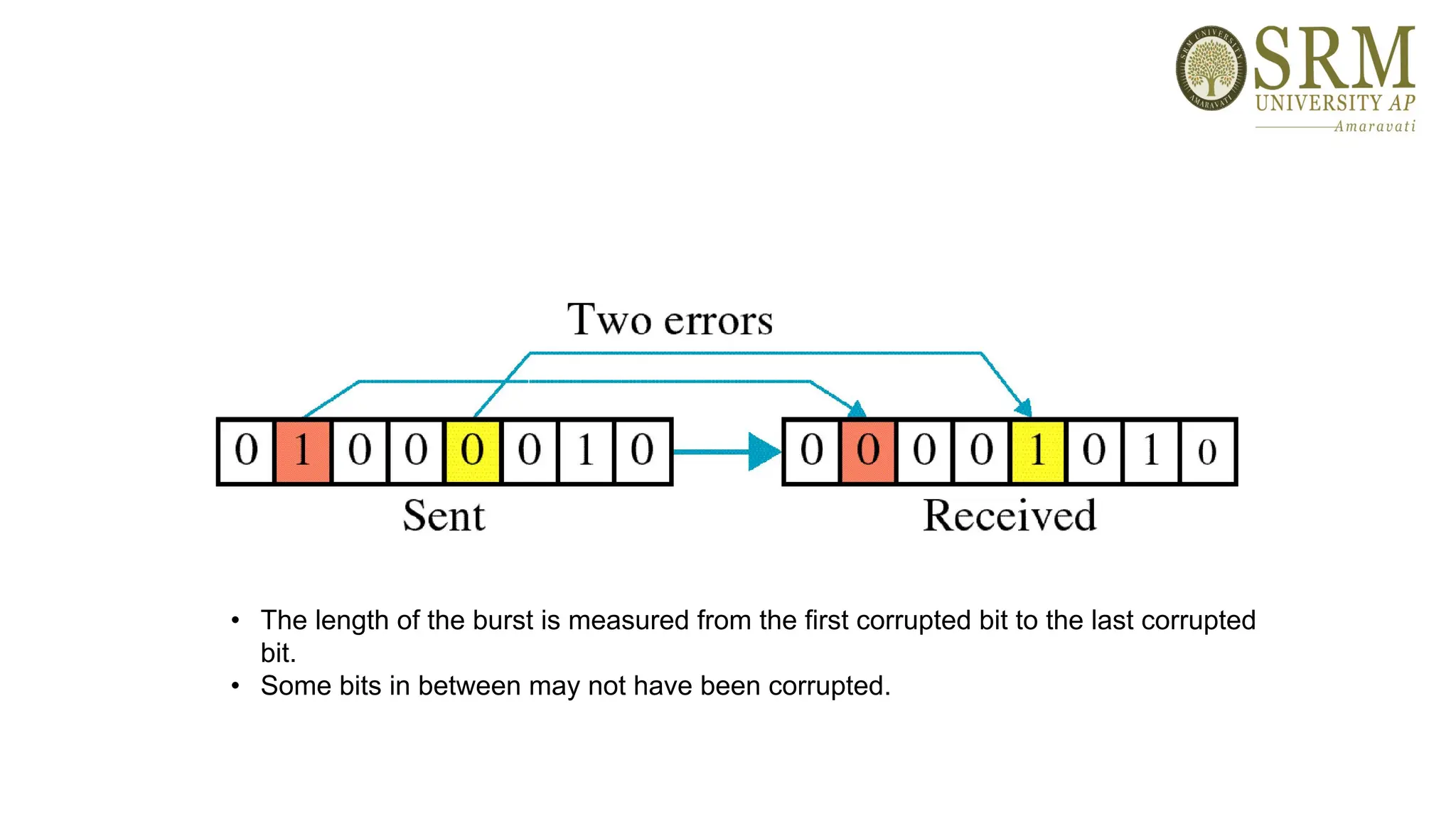
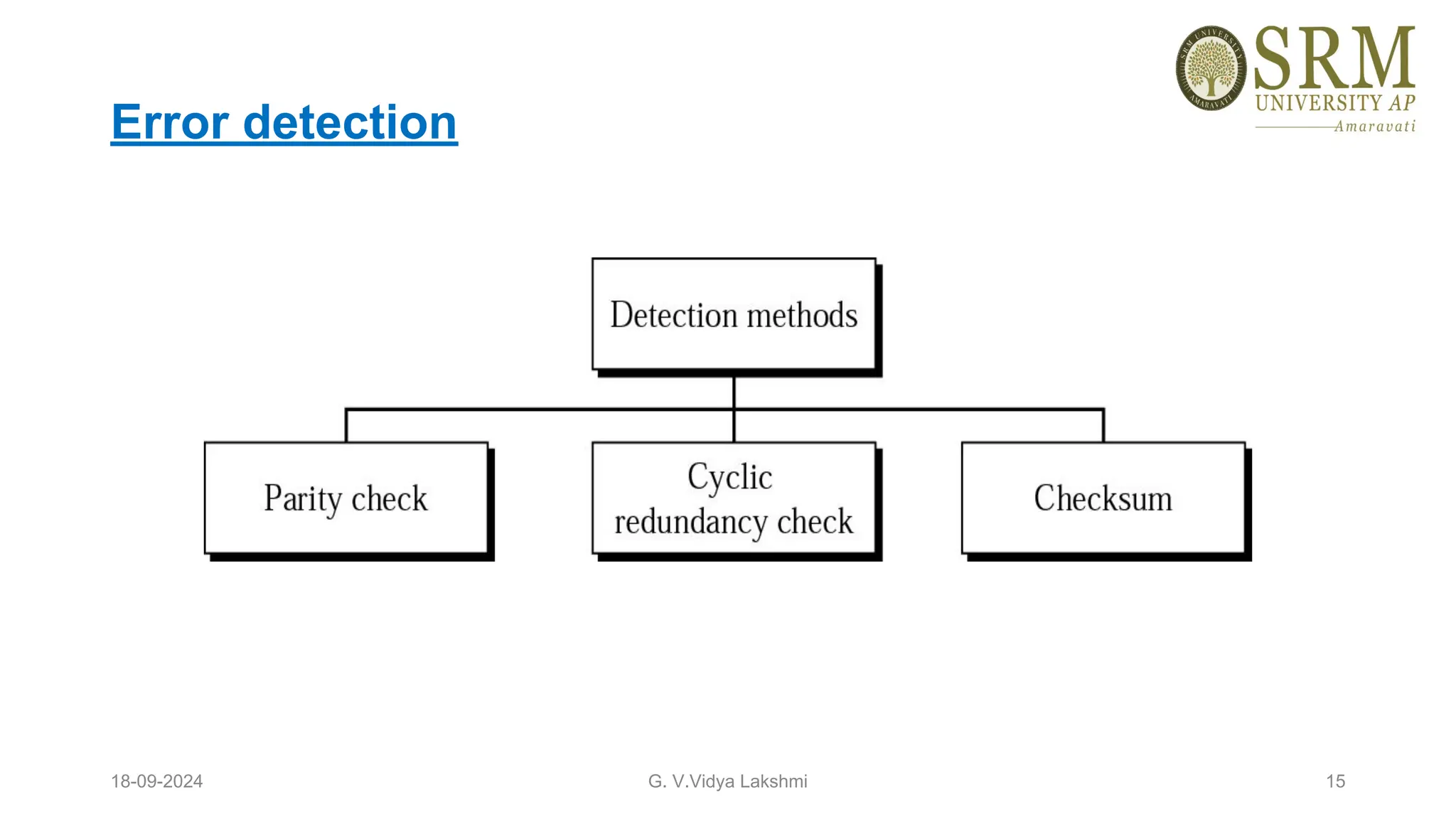
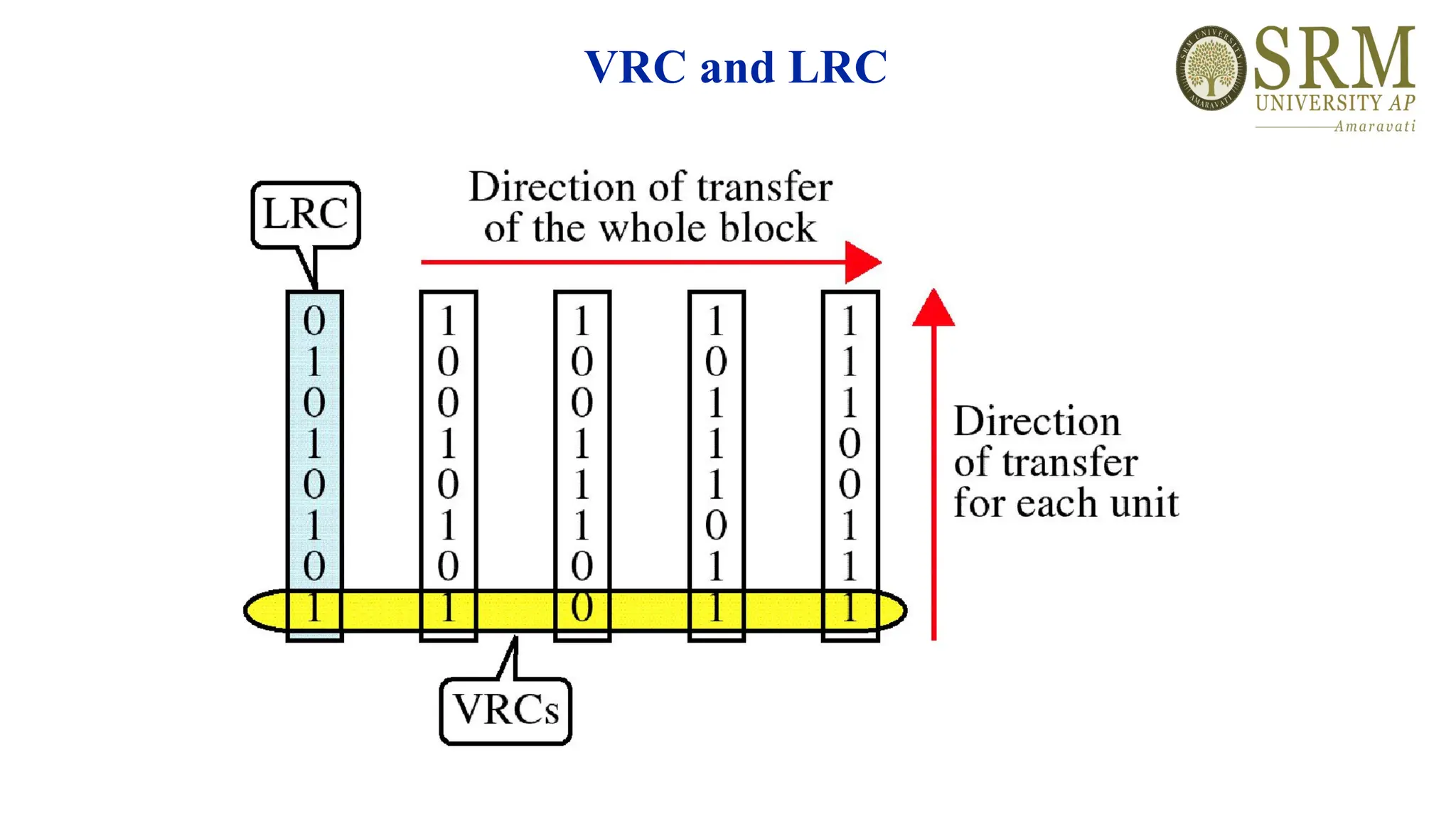
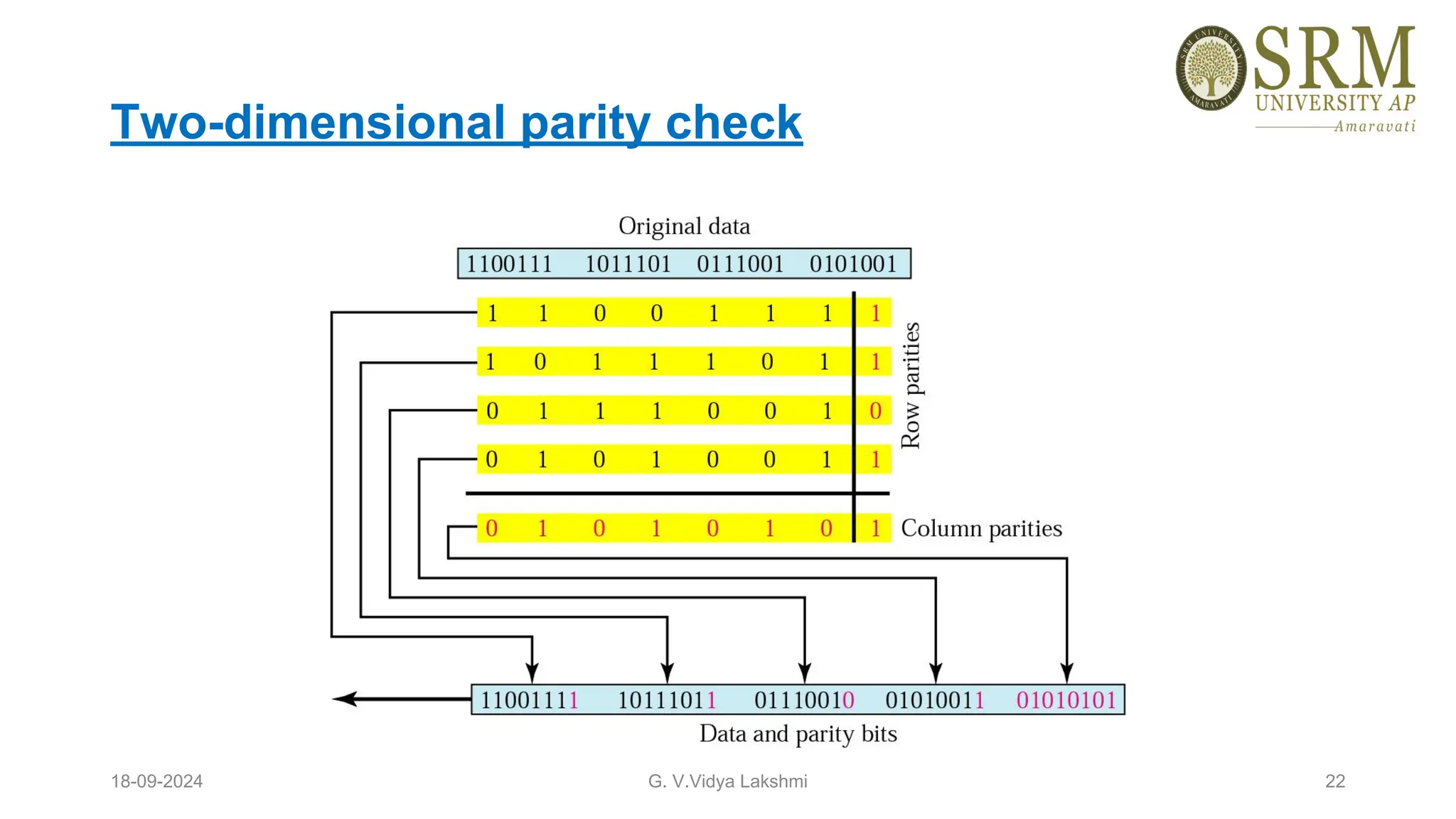
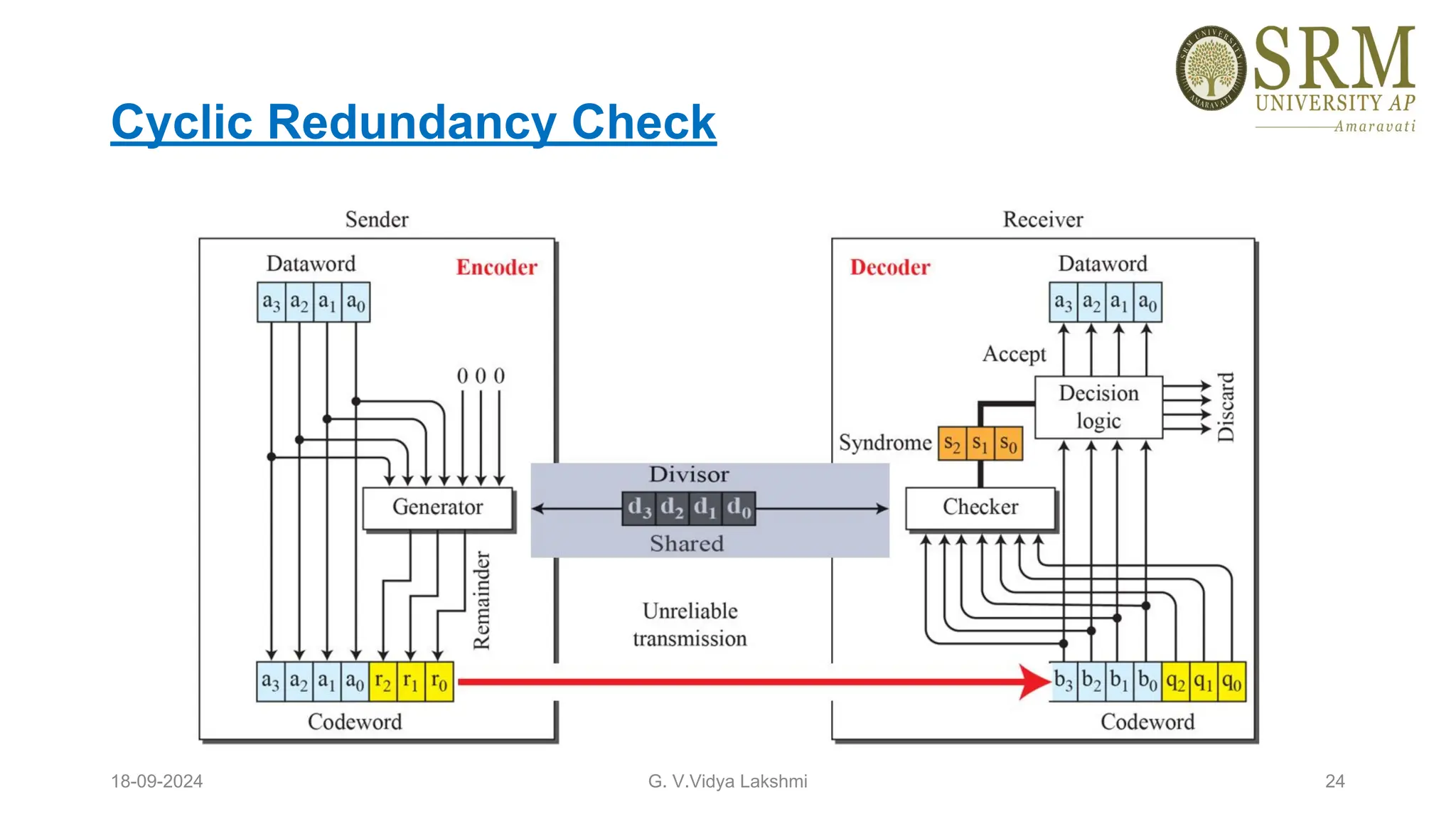
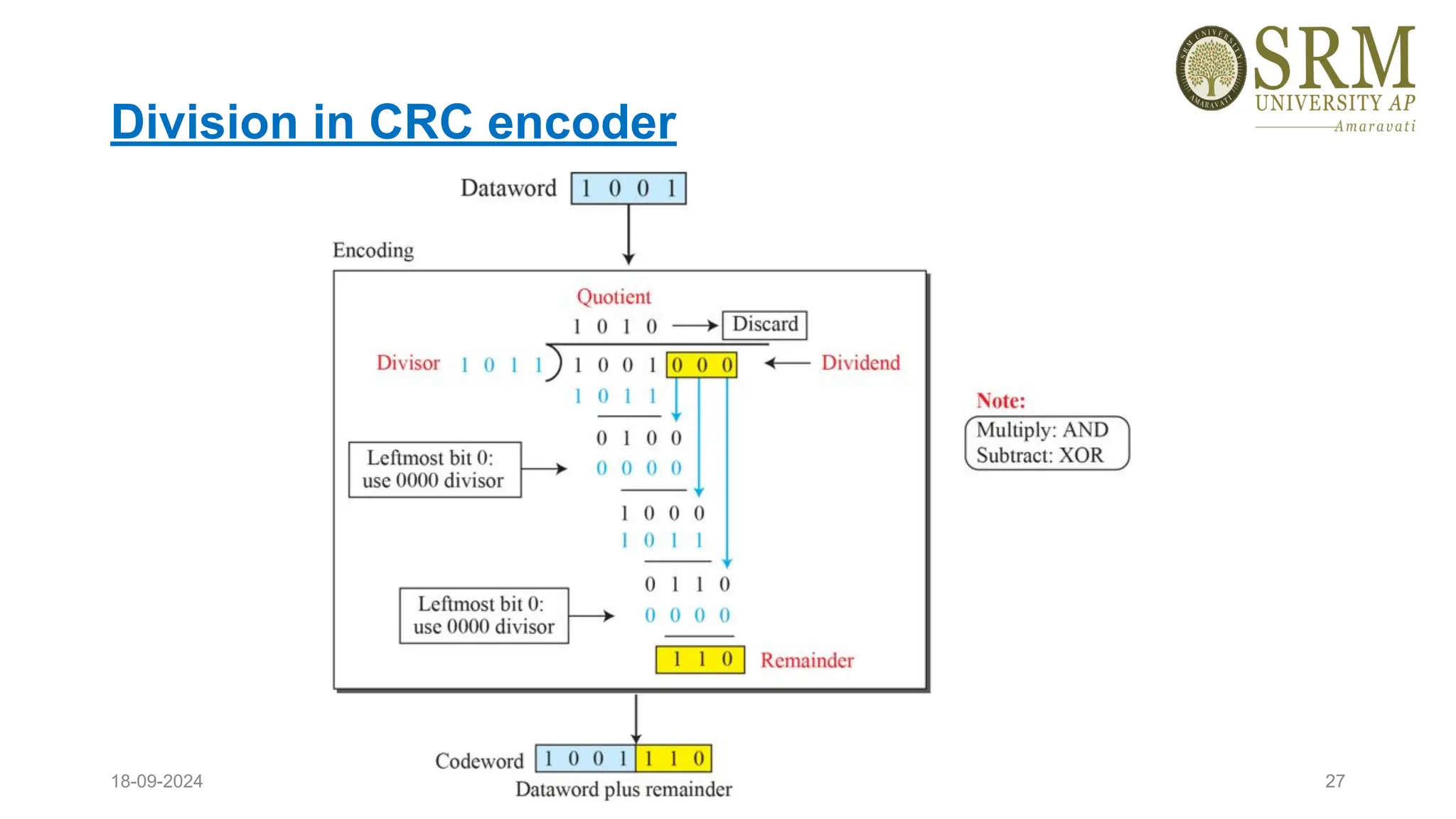
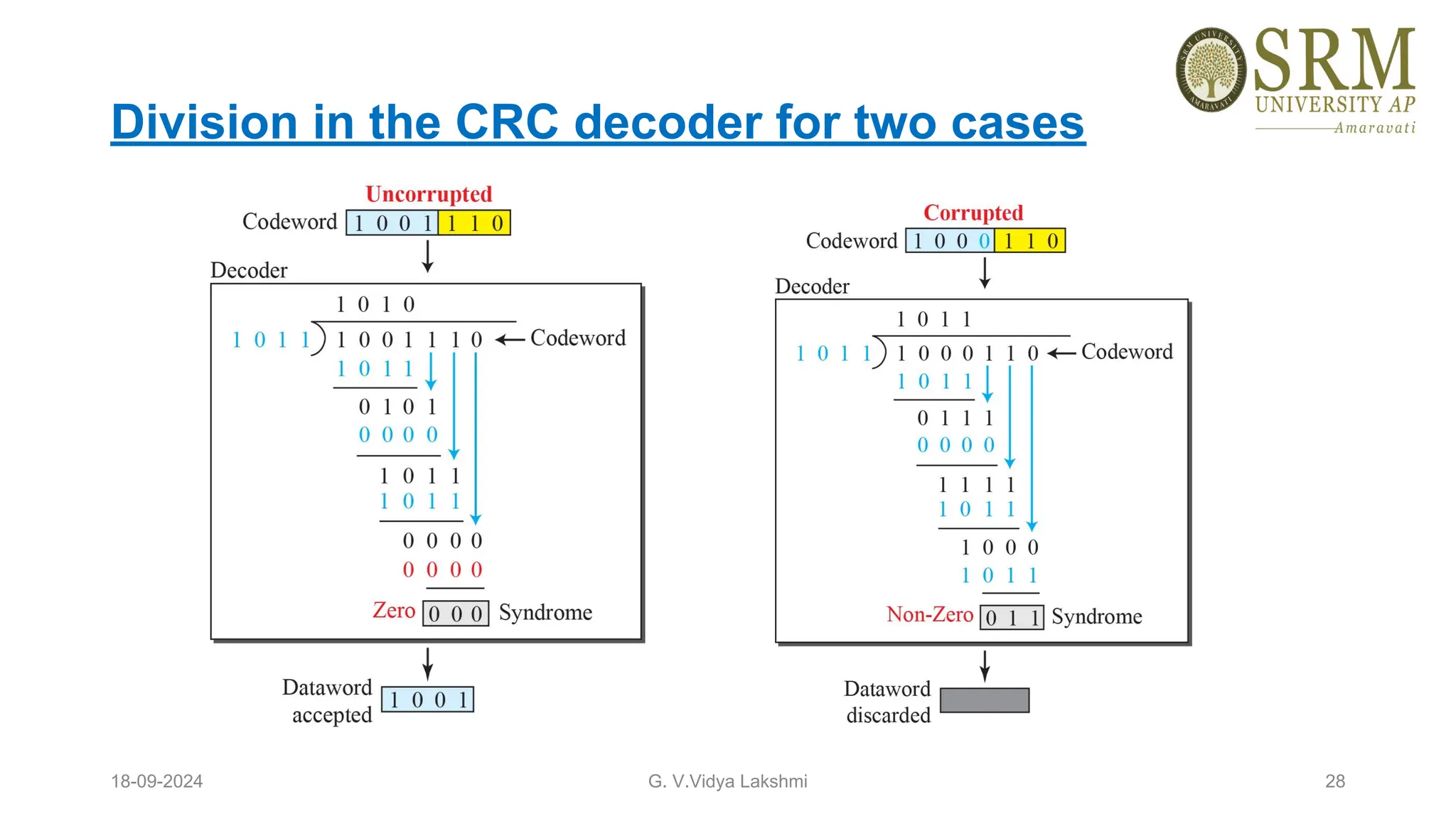
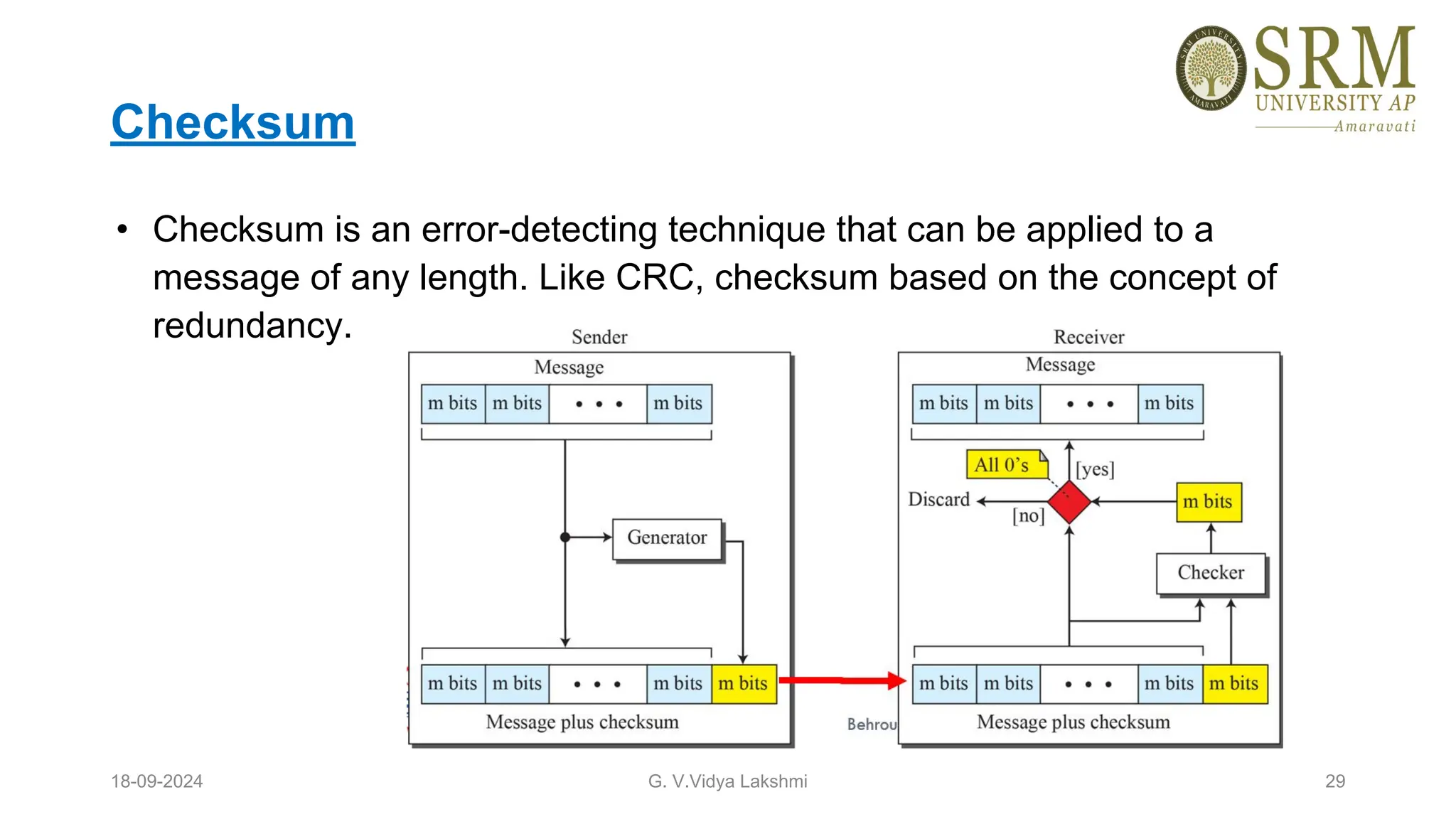
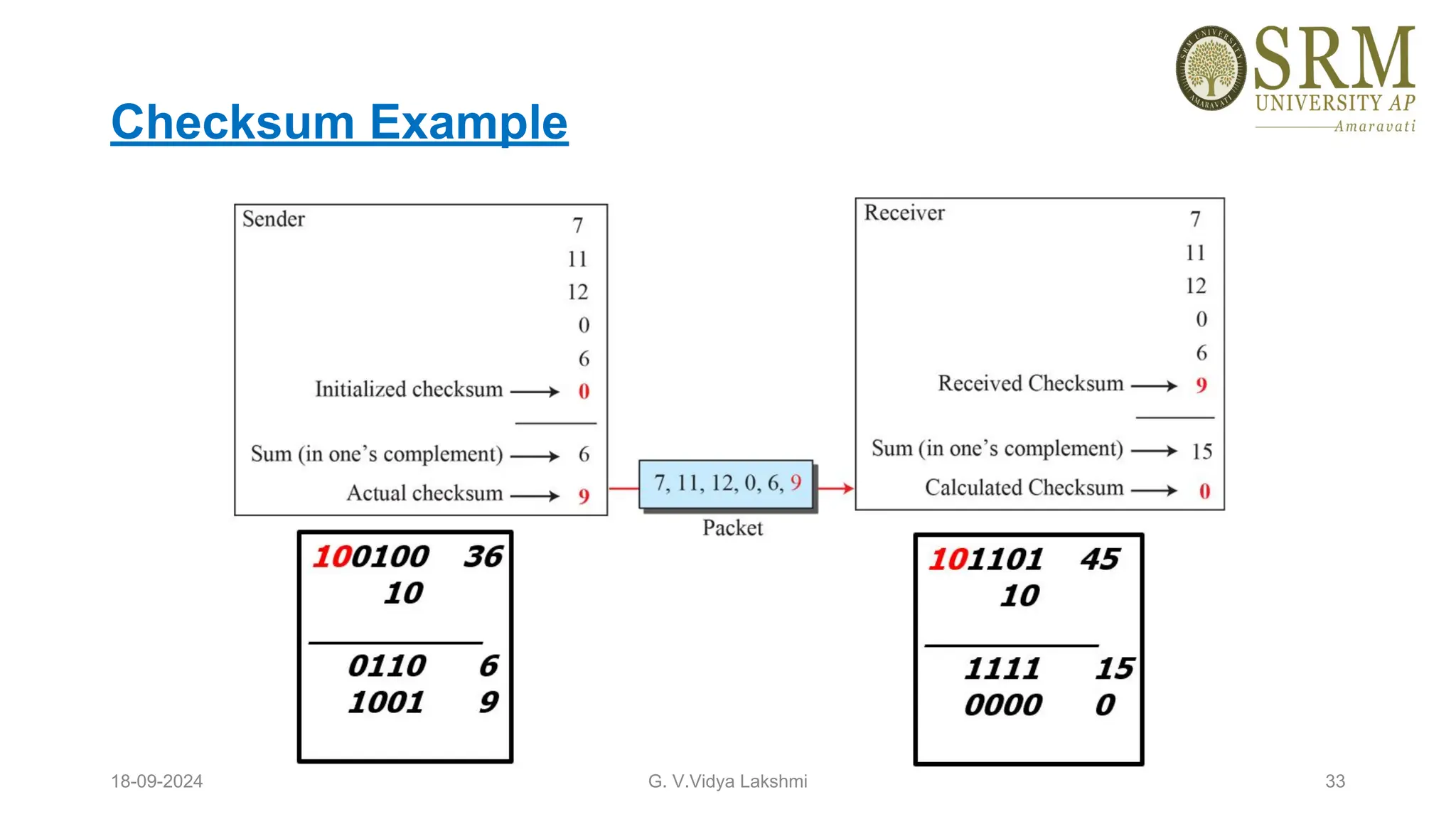
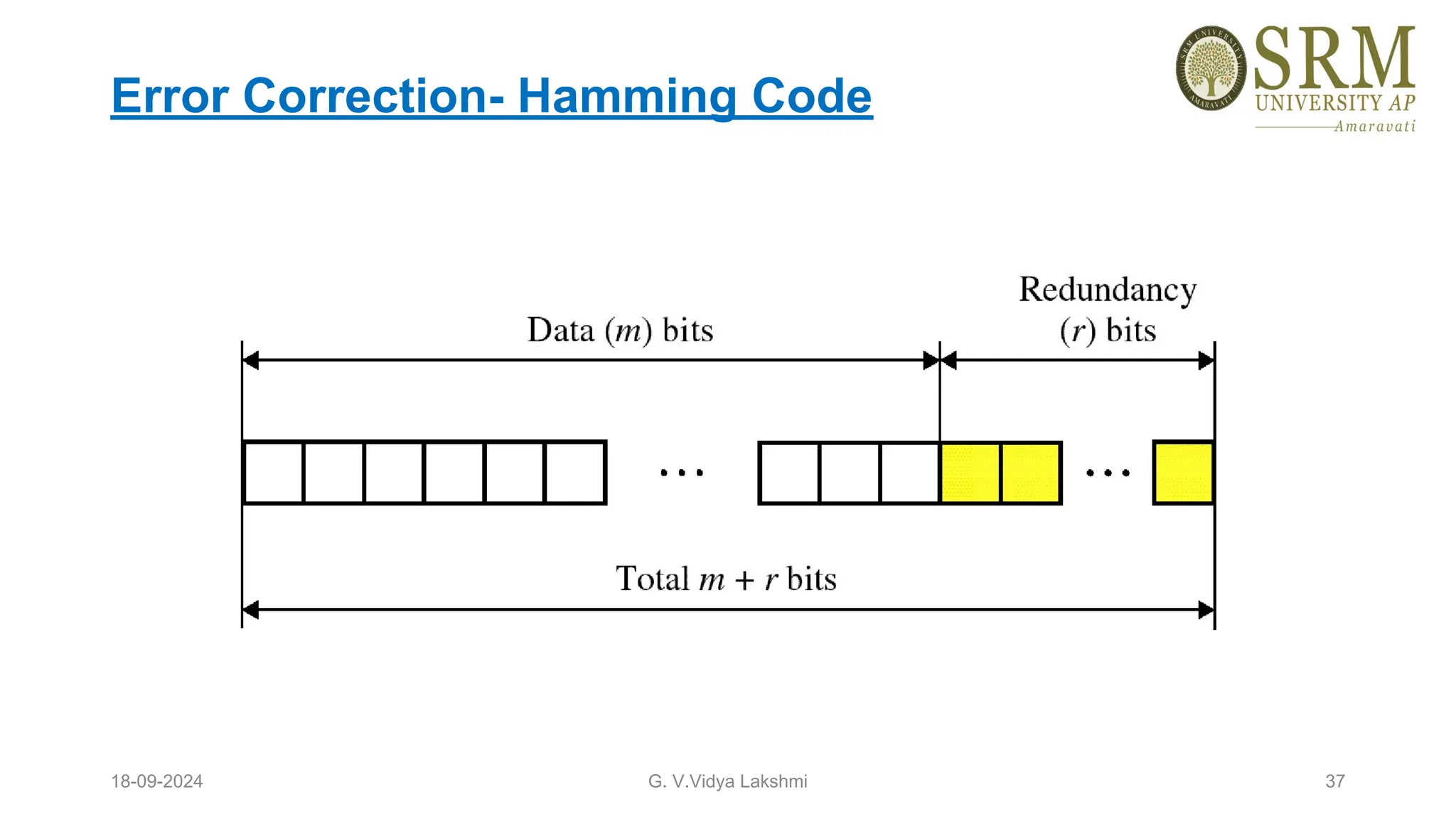
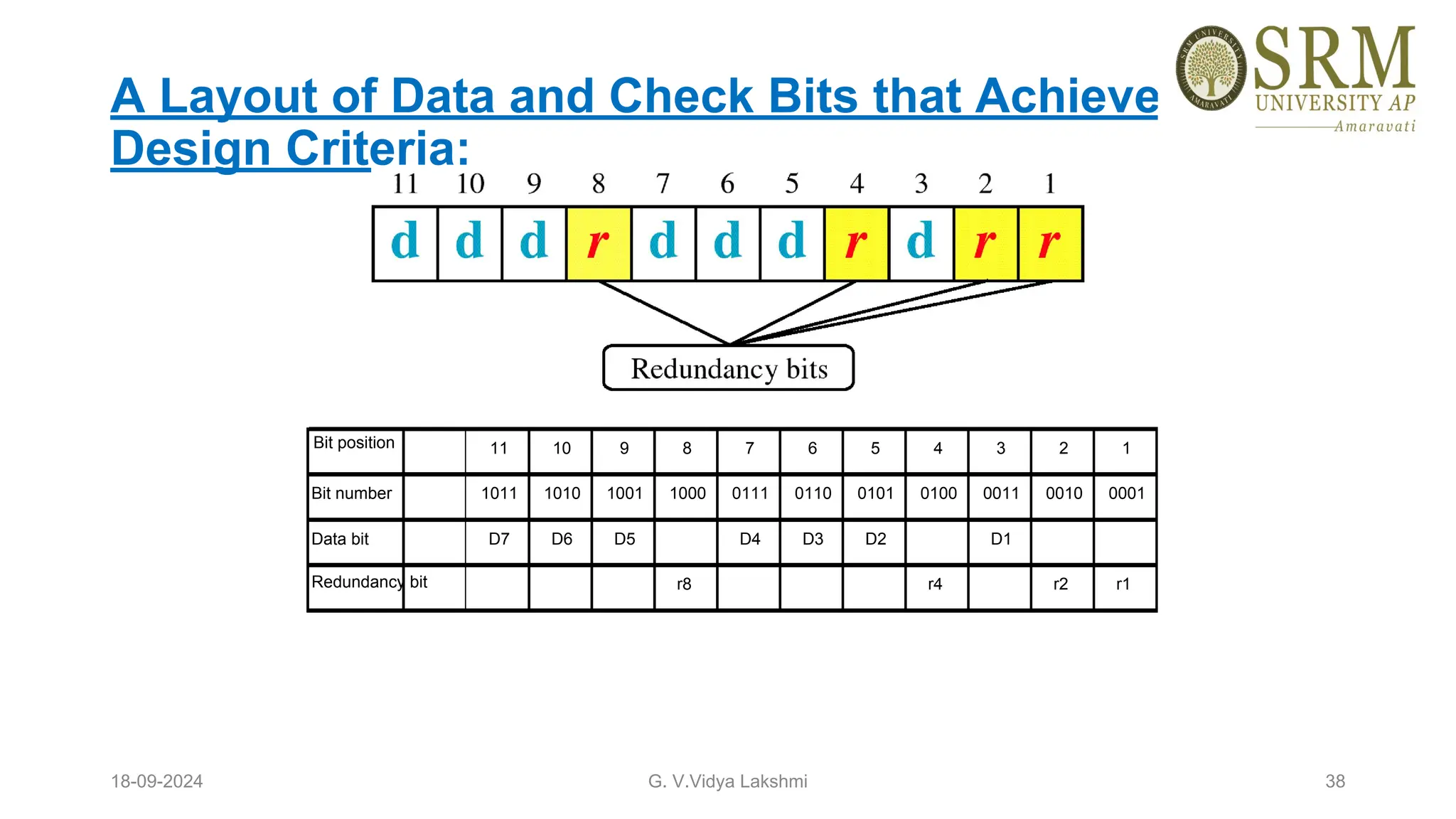
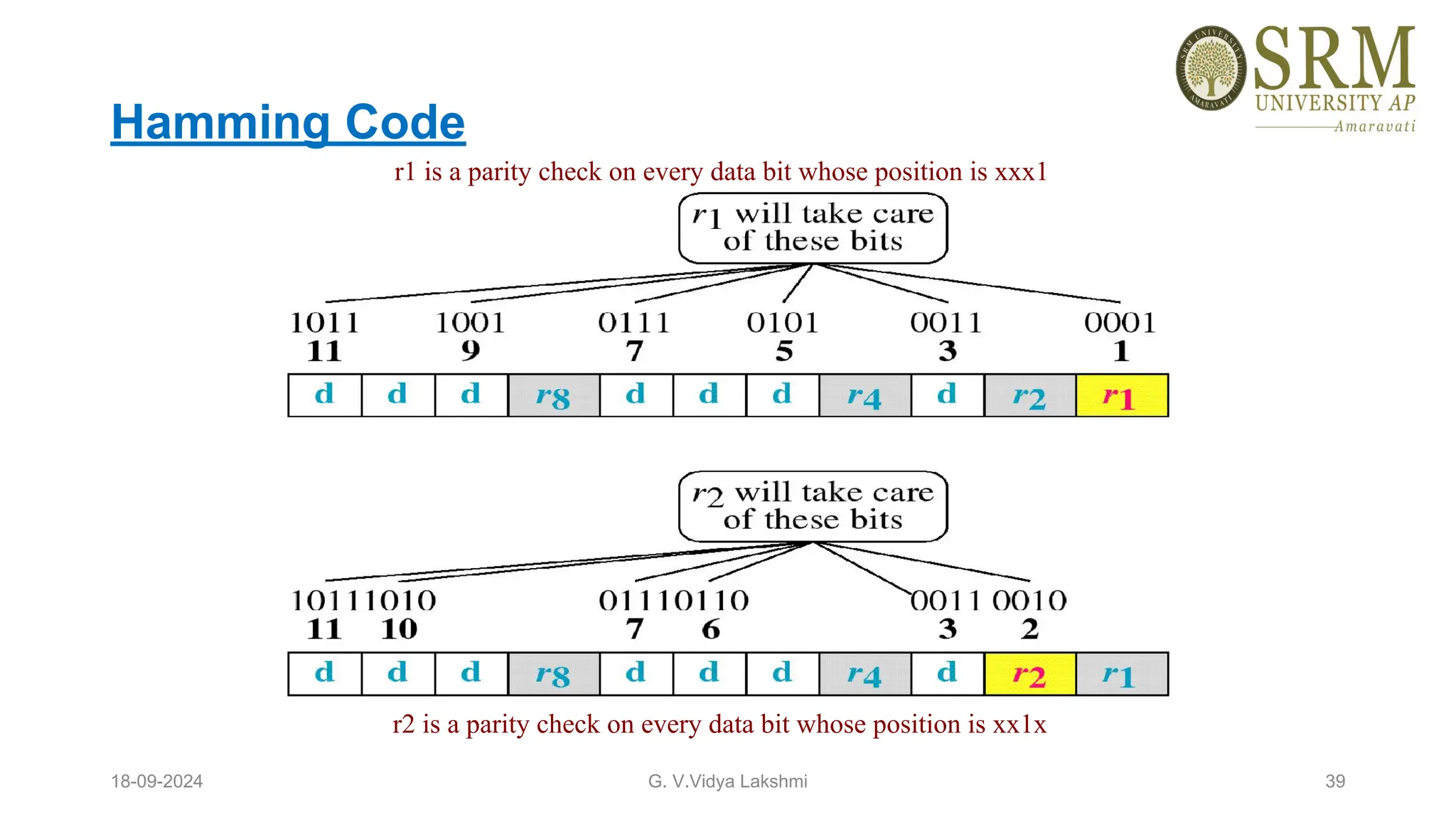
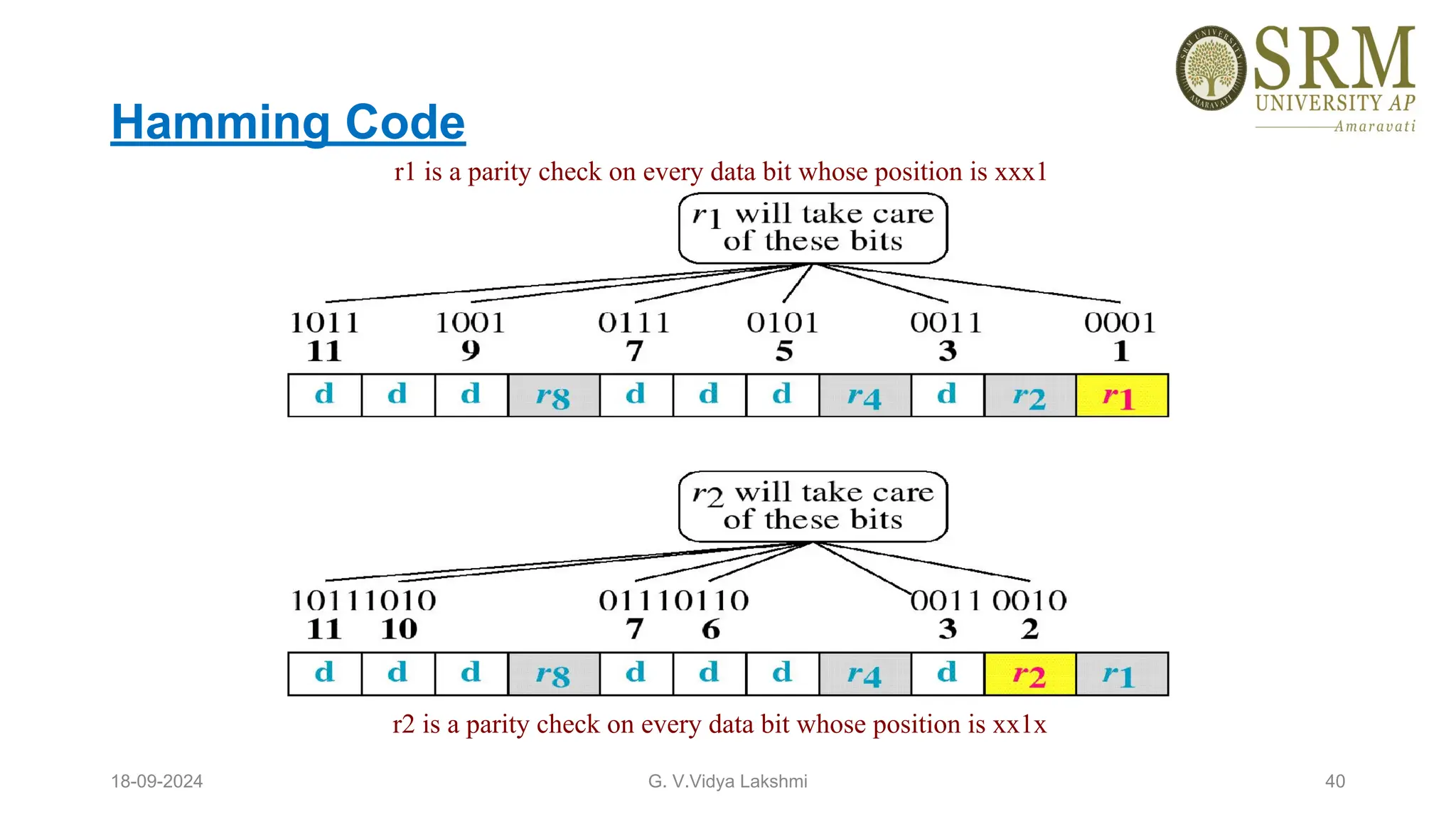
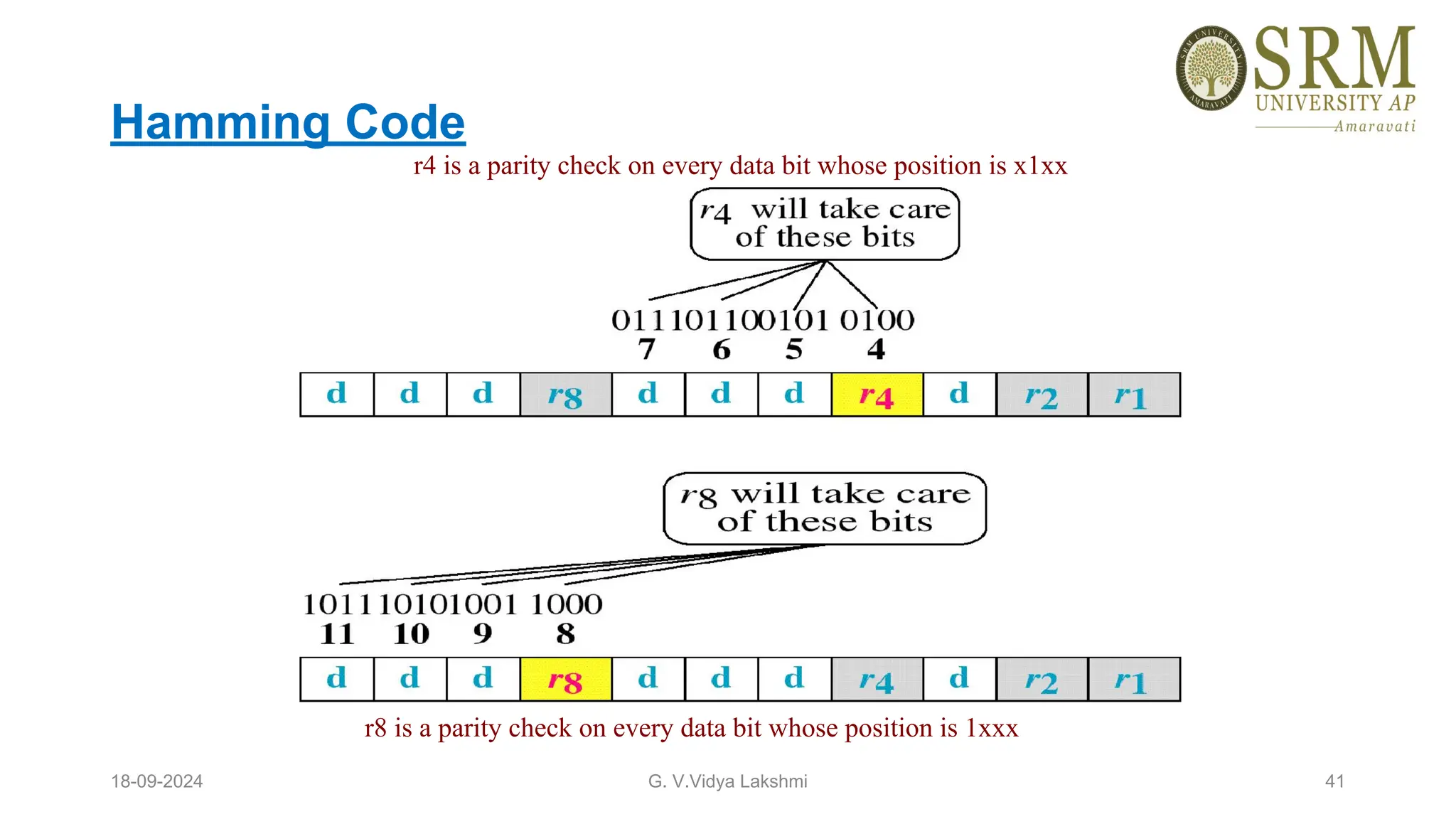
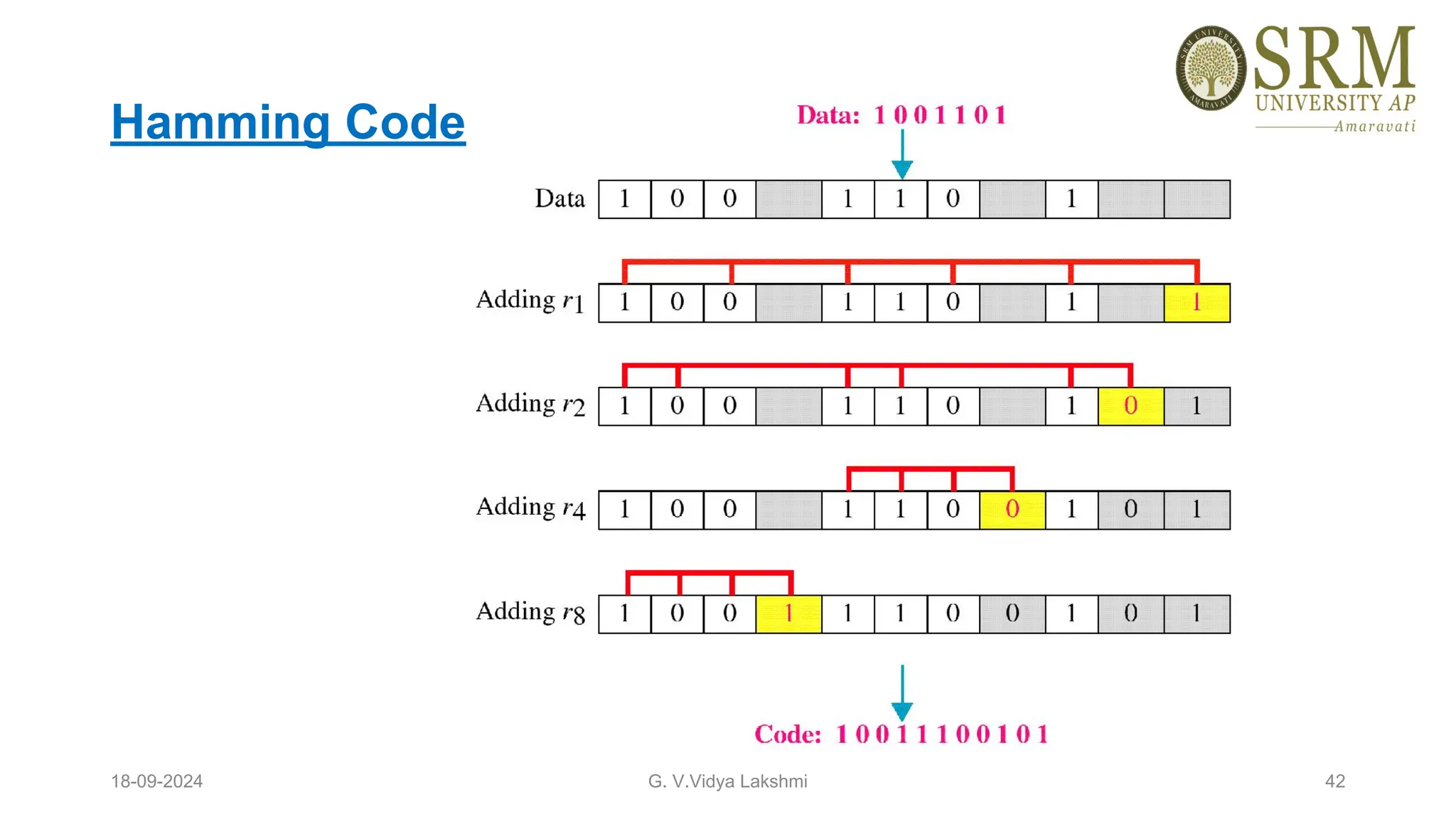
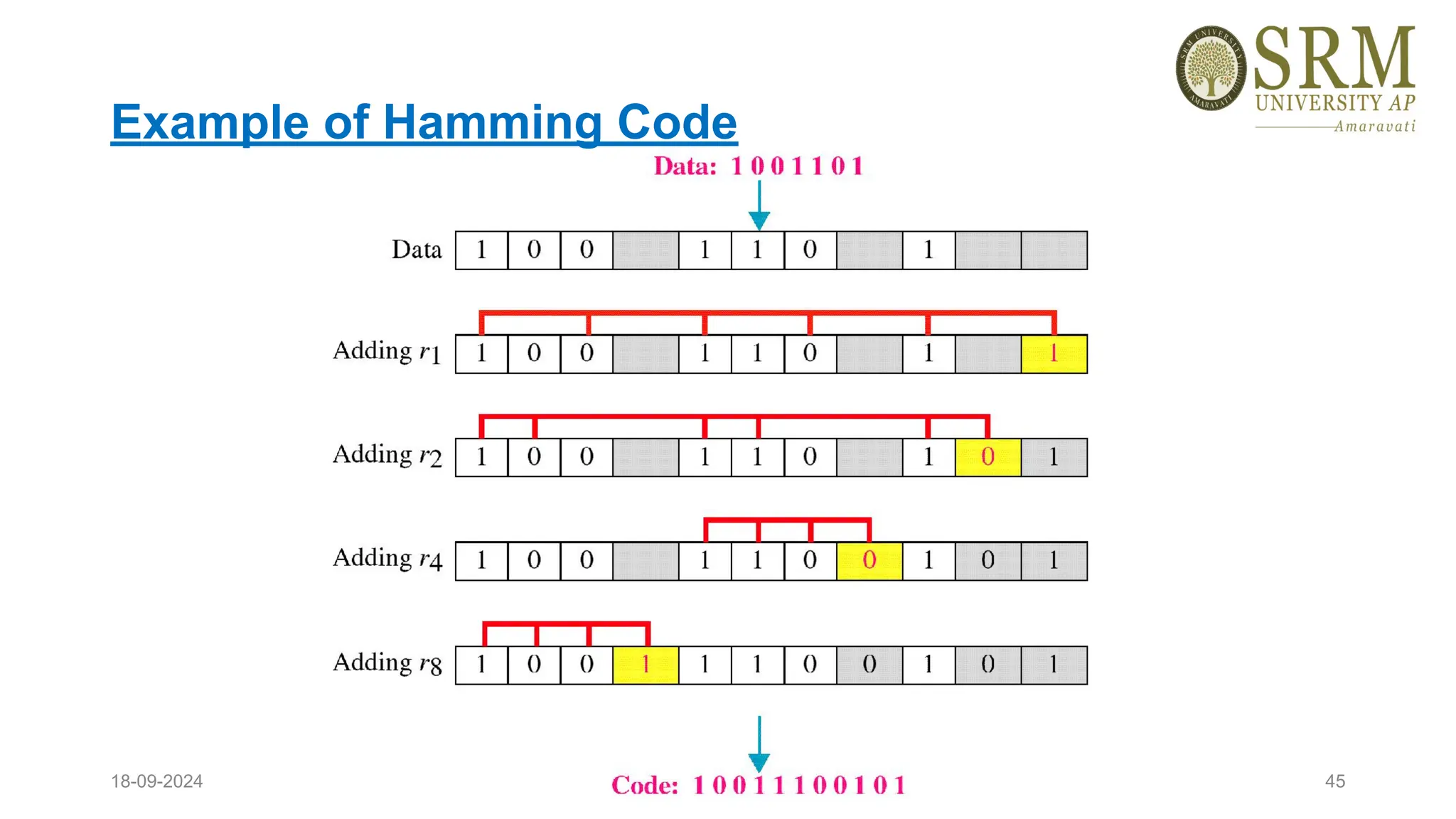
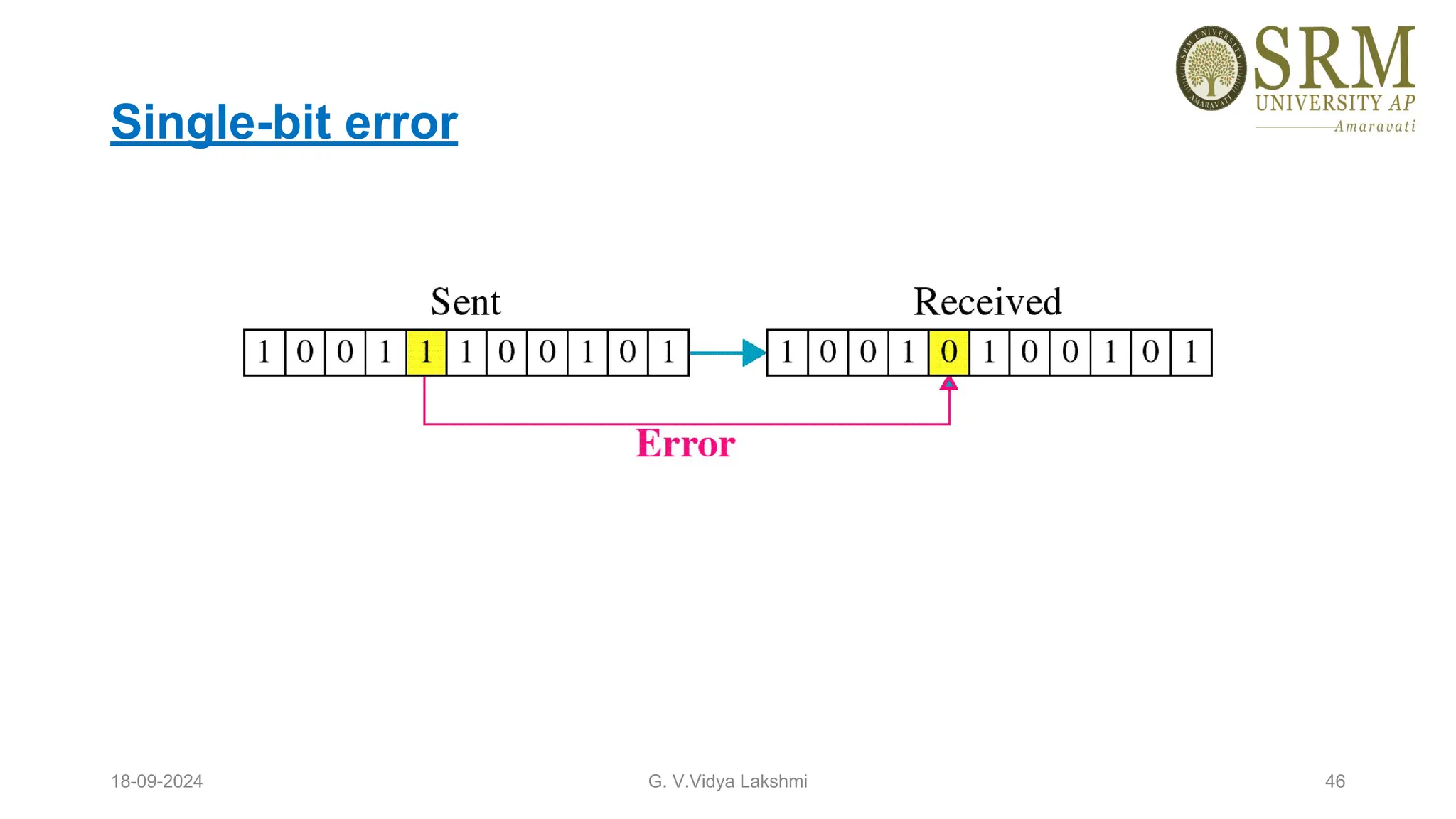
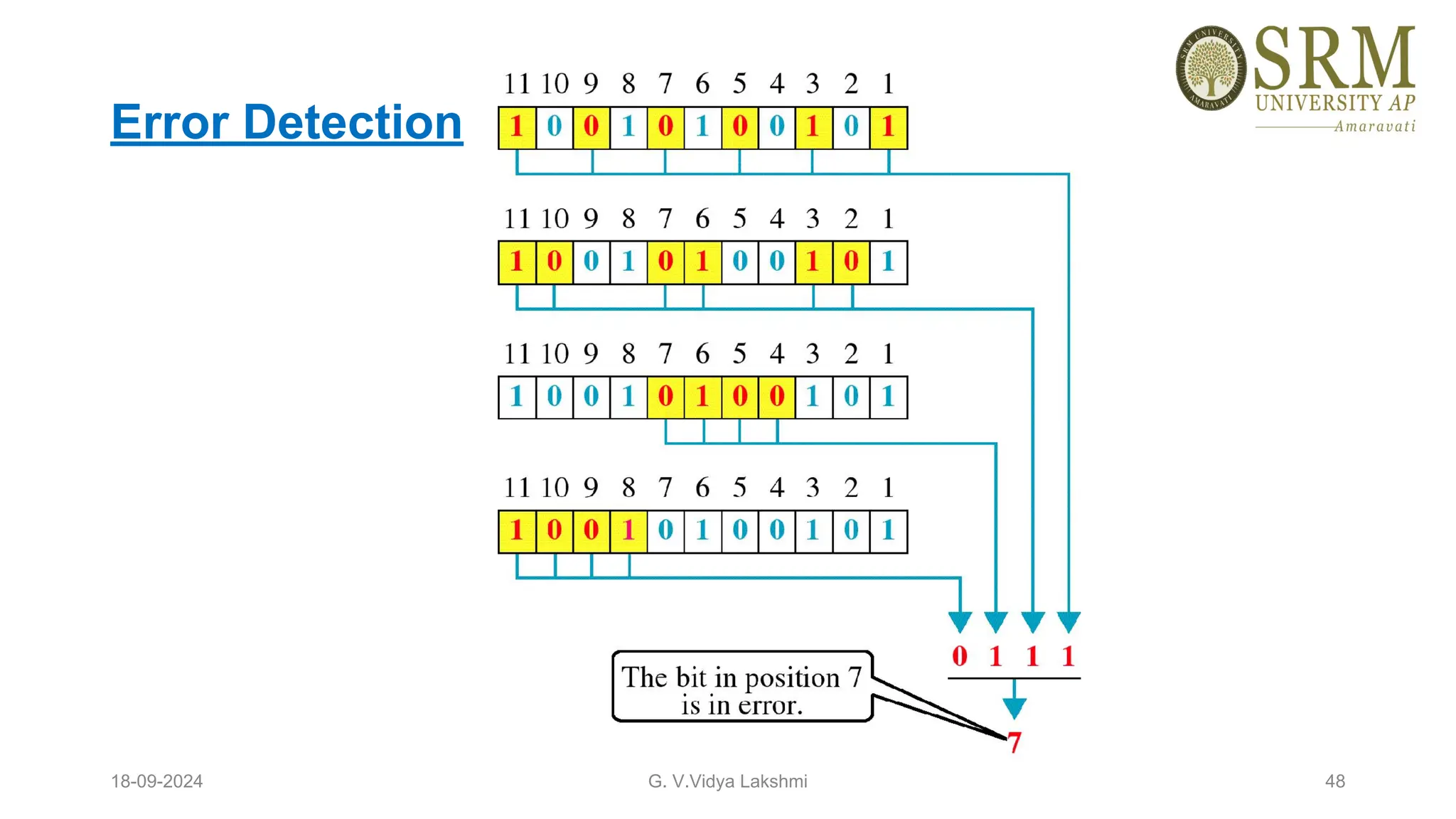
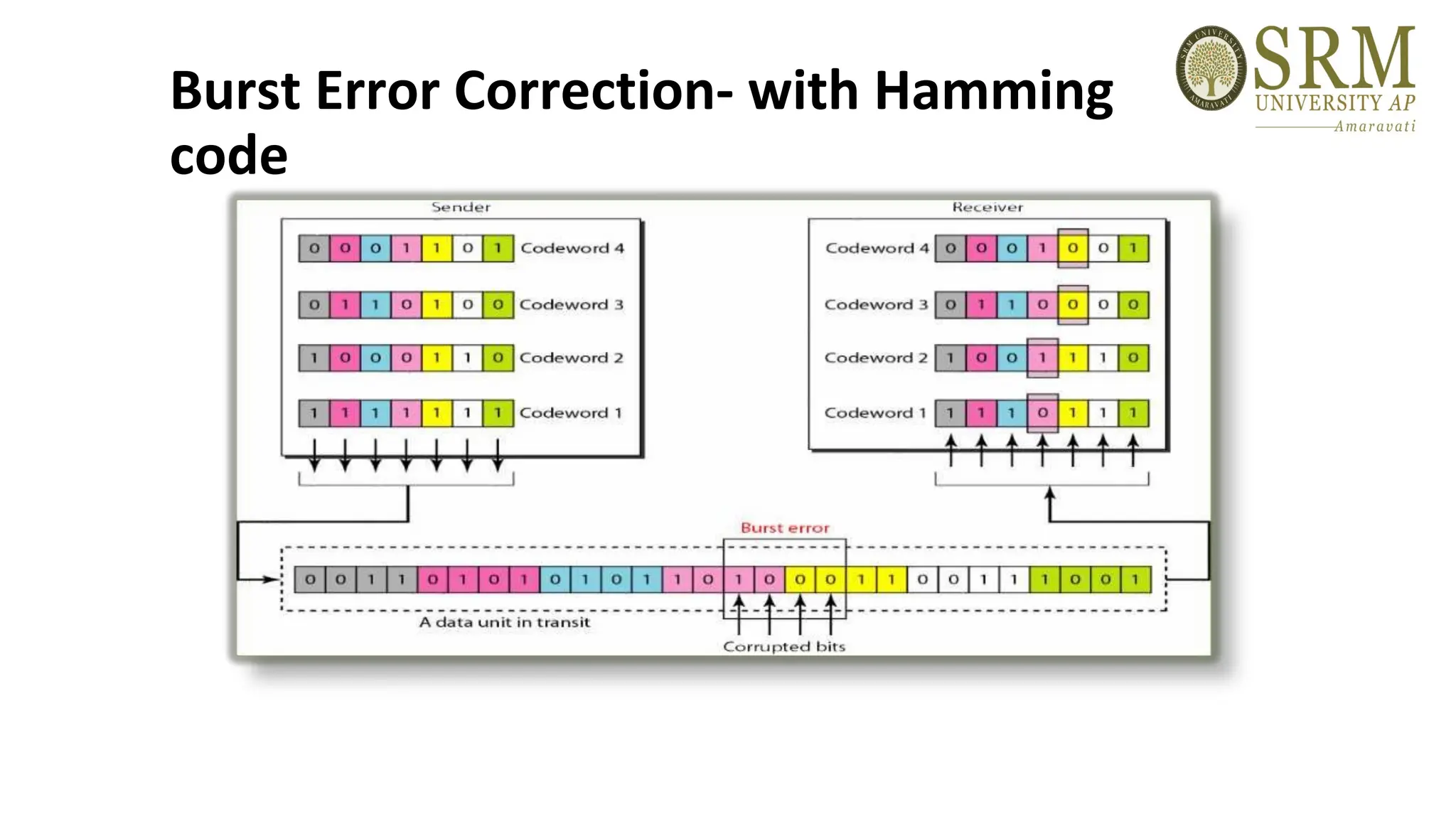
This document discusses error detection and correction methods essential for reliable data transmission in networks. It elaborates on various types of errors, such as single-bit and burst errors, while outlining techniques for detecting and correcting such errors, including redundancy, parity checks, cyclic redundancy checks, checksums, and Hamming codes. The document emphasizes the importance of feedback mechanisms between sender and receiver to ensure data integrity and error correction.