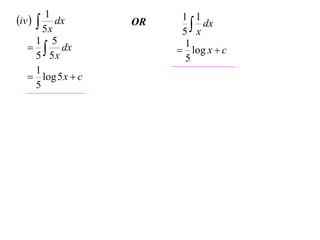
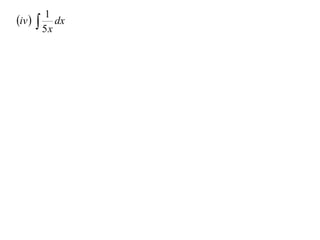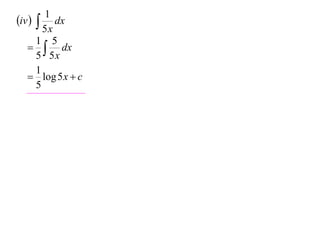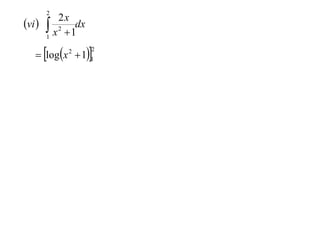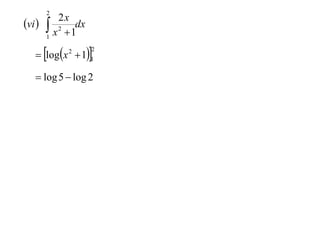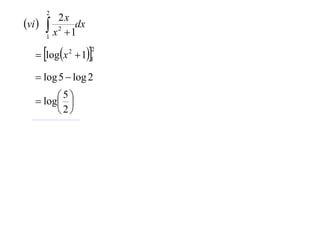The document discusses various techniques for integrating derivatives. It provides examples of integrating common derivatives and explains the steps. Example integrals presented include 1/(7-3x), 8x+5, x5, 1/5x, (4x+1)/(2x+1), ∫x2/(x2+1)dx, and differentiating and integrating x3logx.

1. Integrating Derivative
on Function

2. Integrating Derivative
on Function
f  x 
 f x
dx  log f  x   c

3. Integrating Derivative
on Function
f  x 
 f x
dx  log f  x   c
1
e.g. (i)  7  3x dx

4. Integrating Derivative
on Function
f  x 
 f x
dx  log f  x   c
1
e.g. (i)  7  3x dx
1 3
  dx
3 7  3x

5. Integrating Derivative
on Function
f  x 
 f x
dx  log f  x   c
1
e.g. (i)  7  3x dx
1 3
  dx
3 7  3x
1
  log7  3 x   c
3

6. Integrating Derivative
on Function
f  x 
 f x
dx  log f  x   c
1 dx
e.g. (i)  7  3x dx ii   8x  5
1 3
  dx
3 7  3x
1
  log7  3 x   c
3

7. Integrating Derivative
on Function
f  x 
 f x
dx  log f  x   c
1 dx
e.g. (i)  7  3x dx ii  8x  5
1 3 1 8dx
  dx  
3 7  3x 8 8x  5
1
  log7  3 x   c
3

8. Integrating Derivative
on Function
f  x 
 f x
dx  log f  x   c
1 dx
e.g. (i)  7  3x dx ii  8x  5
1 3 1 8dx
  dx  
3 7  3x 8 8x  5
1 1
  log7  3 x   c  log8 x  5  c
3 8

9. Integrating Derivative
on Function
f  x 
 f x
dx  log f  x   c
e.g. (i)  1 dx ii  
dx x5
iii   6 dx
7  3x 8x  5 x 2
1 3 1 8dx
  dx  
3 7  3x 8 8x  5
1 1
  log7  3 x   c  log8 x  5  c
3 8

10. Integrating Derivative
on Function
f  x 
 f x
dx  log f  x   c
e.g. (i)  1 dx ii  
dx x5
iii   6 dx
7  3x 8x  5 x 2
1 3 1 8dx 1 6 x5
  dx     6 dx
3 7  3x 8 8x  5 6 x 2
1 1
  log7  3 x   c  log8 x  5  c
3 8

11. Integrating Derivative
on Function
f  x 
 f x
dx  log f  x   c
e.g. (i)  1 dx ii  
dx x5
iii   6 dx
7  3x 8x  5 x 2
1 3 1 8dx 1 6 x5
  dx     6 dx
3 7  3x 8 8x  5 6 x 2
 logx 6  2   c
1 1 1
  log7  3 x   c  log8 x  5  c
3 8 6

12. 1
iv   dx
5x

13. 1
iv   dx
5x
1 5
  dx
5 5x

14. 1
iv   dx
5x
1 5
  dx
5 5x
1
 log 5 x  c
5

15. 1
iv   dx OR 1 1
 x dx
5x 5
1 5
  dx
5 5x
1
 log 5 x  c
5

16. 1
iv   dx OR 1 1
 x dx
5x 5
1 5
  dx 1
 log x  c
5 5x 5
1
 log 5 x  c
5

17. 1
iv   dx OR 1 1
 x dx
5x 5
1 5
  dx 1
 log x  c
5 5x 5
1
 log 5 x  c
5
4x 1
v   dx
2x 1

18. 1
iv   dx OR 1 1
 x dx
5x 5
1 5
  dx 1
 log x  c
5 5x 5
1
 log 5 x  c
5
4x 1 order numerator  order denominator
v   dx
2x 1

19. 1
iv   dx OR 1 1
 x dx
5x 5
1 5
  dx 1
 log x  c
5 5x 5
1
 log 5 x  c
5
4x 1 order numerator  order denominator
v   dx
 polynomial division
2x 1

20. 1
iv   dx OR 1 1
 x dx
5x 5
1 5
  dx 1
 log x  c
5 5x 5
1
 log 5 x  c
5
4x 1 order numerator  order denominator
v   dx
 polynomial division
2x 1
2
2x 1 4x 1
4x  2
1

21. 1
iv   dx OR 1 1
 x dx
5x 5
1 5
  dx 1
 log x  c
5 5x 5
1
 log 5 x  c
5
4x 1 order numerator  order denominator
v   dx
 polynomial division
2x 1
 2  1  dx 2
 2 x  1 2x 1 4x 1
4x  2
1

22. 1
iv   dx OR 1 1
 x dx
5x 5
1 5
  dx 1
 log x  c
5 5x 5
1
 log 5 x  c
5
4x 1 order numerator  order denominator
v   dx
 polynomial division
2x 1
 2  1  dx 2
 2 x  1 2x 1 4x 1
1 4x  2
 2 x  log2 x  1  c
2 1

23. 2
2x
vi   x 2  1dx
1

24. 2
2x
vi   x 2  1dx
1
 logx  11
2 2

25. 2
2x
vi   x 2  1dx
1
 logx  11
2 2
 log 5  log 2

26. 2
2x
vi   x 2  1dx
1
 logx  11
2 2
 log 5  log 2
 log 
5
 
2

27. 2
vi  2x
 x 2  1dx vii  Differentiate x 3 log x and hence
1
integrate x 2 log x
 logx  11
2 2
 log 5  log 2
 log 
5
 
2

28. 2
vi  2x
 x 2  1dx vii  Differentiate x 3 log x and hence
1
integrate x 2 log x
 logx  11
2
x log x  x    log x 3x 2 
3 1
2
d 3
dx  x
 log 5  log 2
 log 
5
 
2

29. 2
vi  2x
 x 2  1dx vii  Differentiate x 3 log x and hence
1
integrate x 2 log x
 logx  11
2
x log x  x    log x 3x 2 
3 1
2
d 3
dx  x
 log 5  log 2
 x 2  3 x 2 log x
 log 
5
 
2

30. 2
vi  2x
 x 2  1dx vii  Differentiate x 3 log x and hence
1
integrate x 2 log x
 logx  11
2
x log x  x    log x 3x 2 
3 1
2
d 3
dx  x
 log 5  log 2
 x 2  3 x 2 log x
 log 
5
 x  3 x 2 log x dx  x 3 log x  c
  2
2

31. 2
vi  2x
 x 2  1dx vii  Differentiate x 3 log x and hence
1
integrate x 2 log x
 logx  11
2
x log x  x    log x 3x 2 
3 1
2
d 3
dx  x
 log 5  log 2
 x 2  3 x 2 log x
 log 
5
 x  3 x 2 log x dx  x 3 log x  c
  2
2
3 x 2 log xdx  x 3 log x   x 2 dx  c

32. 2
vi  2x
 x 2  1dx vii  Differentiate x 3 log x and hence
1
integrate x 2 log x
 logx  11
2
x log x  x    log x 3x 2 
3 1
2
d 3
dx  x
 log 5  log 2
 x 2  3 x 2 log x
 log 
5
 x  3 x 2 log x dx  x 3 log x  c
  2
2
3 x 2 log xdx  x 3 log x   x 2 dx  c
1 3 1 3
 x log xdx  3 x log x  9 x  c
2

33. 2
vi  2x
 x 2  1dx vii  Differentiate x 3 log x and hence
1
integrate x 2 log x
 logx  11
2
x log x  x    log x 3x 2 
3 1
2
d 3
dx  x
 log 5  log 2
 x 2  3 x 2 log x
 log 
5
 x  3 x 2 log x dx  x 3 log x  c
  2
2
3 x 2 log xdx  x 3 log x   x 2 dx  c
1 3 1 3
 x log xdx  3 x log x  9 x  c
2
Exercise 12D; 1 to 12 ace in all, 14a*
Exercise 12E; 1 to 6 all, 7 to 21 odds, 22abc*, 23*