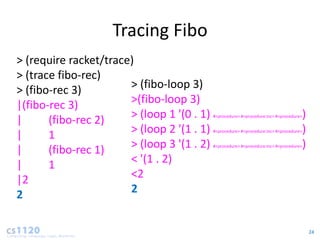
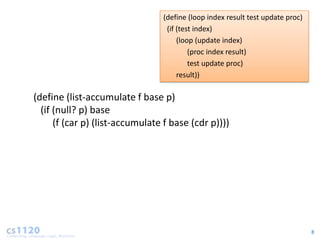
Here are the key points about how evaluation cost scales with input size: - For many algorithms, if the input size increases by a factor of k, the running time increases by a factor of k or faster. This is called polynomial time. - For recursive algorithms like fibonacci, the running time increases exponentially with input size. Each additional input doubles the number of recursive calls. - Space usage also often scales with input size. Recursive algorithms use additional stack space proportional to recursion depth, which grows with input. - Caching/memoization can improve scaling by reusing results of subproblems. But it increases space usage. - Data structure choice matters - hash tables allow O(1) access vs

1. Class 17:
Golden
Sneezewort
cs1120 Fall 2011
David Evans
30 September 2011

2. Plan
Generalizing Loops
Introducing Cost
Book: Chapter 7 and 8
(okay to read after Exam 1)
Not covered on Exam 1
2

3. Recap/Wake-up: A General Loop
(define (loop index result test update proc)
3

4. General Loop with Result
(define (loop index result test update proc)
(if (test index)
(loop (update index)
(proc index result)
test update proc)
result))
4

5. Using Loop
(define (loop index result test update proc)
(if (test index)
(loop (update index)
(proc index result)
test update proc)
result))
(define (gauss-sum n)
(loop 1 0 (lambda (i) (<= i n))
(lambda (i) (+ i 1))
(lambda (i res) (+ res i))))
5

6. (define (loop index result test update proc)
(if (test index)
(loop (update index)
(proc index result)
test update proc)
result))
(define (factorial n)
6

7. (define (loop index result test update proc)
(if (test index)
(loop (update index)
(proc index result)
test update proc)
result))
(define (list-length p)
7

8. (define (loop index result test update proc)
(if (test index)
(loop (update index)
(proc index result)
test update proc)
result))
(define (list-accumulate f base p)
(if (null? p) base
(f (car p) (list-accumulate f base (cdr p))))
8

9. (define (loop index result test update proc)
(if (test index)
(loop (update index)
(proc index result)
test update proc)
result))
(define (list-accumulate f base p)
(if (null? p) base
(f (car p) (list-accumulate f base (cdr p))))
(define (list-accumulate f base p)
(loop p base not-null? cdr (lambda (p res) (f (car p) res))))
9

10. Challenge Problem
Define an efficient edit-distance
procedure (as defined in PS2) using
loop (without using memoization).
10

11. Sneezewort!
11

12. Sneezewort Growth
First Time Unit Second Time Unit Offshoot
Could we model Sneezewort with PS3 code?
12

13. Sneezewort Numbers
13
8?
5
3
2
1
1
13

14. Page from
Liber abbaci,
Leonardo da Pisa
(1202)
14

15. Fibonacci’s Problem
Suppose a newly-born pair of rabbits, one
male, one female, are put in a field.
Rabbits mate at the age of one month so
that at the end of its second month a
female can produce another pair of
rabbits.
Suppose that our rabbits never die and
that the female always produces one new
pair (one male, one female) every month
from the second month on.
How many pairs will there be in one year? Filius Bonacci, 1202 (Pisa)
Liber Abaci (“Book of Calculation”)
15

16. Rabbits
From http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibnat.html
16

17. Fibonacci Numbers
GEB p. 136:
These numbers are best defined
recursively by the pair of formulas
FIBO (n) = FIBO (n – 1) + FIBO (n – 2)
for n > 2
FIBO (1) = FIBO (2) = 1
Can we turn this into a Scheme procedure?
17

18. Defining FIBO
These numbers defined
recursively by:
FIBO (n) =
FIBO (n – 1)
+ FIBO (n – 2)
for n > 1
FIBO (1) = 1
FIBO (0) = 0
18

19. Defining fibo
(define (fibo n) > (fibo 1)
1
(if (= n 0) 0
> (fibo 2)
(if (= n 1) 1 2
(+ (fibo (- n 1)) > (fibo 3)
3
(fibo (- n 2)))))) > (fibo 10)
55
19

20. Defining fibo with loop?
(define (loop index result test update proc)
(if (test index)
(loop (update index)
(proc index result)
test update proc)
result))
20

21. (define (fibo-loop n) ; doesn't work for n=0
(cdr
(loop 1
(cons 0 1)
(lambda (i) (< i n))
inc
(lambda (i v) (cons (cdr v) (+ (car v) (cdr v)))))))
21

22. Which is better?
(define (fibo-rec n)
(if (= n 0) 0
(if (= n 1) 1
(+ (fibo-rec (- n 1)) (fibo-rec (- n 2))))))
(define (fibo-loop n) ; doesn't work for n=0
(cdr
(loop 1 (cons 0 1) (lambda (i) (< i n)) inc
(lambda (i v) (cons (cdr v) (+ (car v) (cdr v)))))))
22

23. Fibo Results
> (fibo-rec 2)
1
> (fibo-rec 3)
2
> (fibo-rec 4)
3
> (fibo-rec 10)
55
> (fibo-rec 60)
Still working…
23

24. Tracing Fibo
> (require racket/trace)
> (trace fibo-rec)
> (fibo-rec 3) > (fibo-loop 3)
|(fibo-rec 3) >(fibo-loop 3)
| (fibo-rec 2) > (loop 1 '(0 . 1) #<procedure> #<procedure:inc> #<procedure> )
| 1 > (loop 2 '(1 . 1) #<procedure> #<procedure:inc> #<procedure> )
| (fibo-rec 1) > (loop 3 '(1 . 2) #<procedure> #<procedure:inc> #<procedure> )
| 1 < '(1 . 2)
|2 <2
2 2
24

25. > (fibo-rec 4)
>(fibo-rec 4)
> (fibo-rec 3)
> >(fibo-rec 2)
> > (fibo-rec 1)
<<1 To compute (fibo 4) we calculated:
> > (fibo-rec 0)
<<0 (fibo 3) 1 times
< <1 (fibo 2) 2 times
> >(fibo-rec 1) (fibo 1) 3 times
< <1
<2 (fibo 0) 3 times
> (fibo-rec 2) = 3+6 calls to fibo
> >(fibo-rec 1)
< <1 How many calls to calculate (fibo 60)?
> >(fibo-rec 0)
< <0
<1
<3
3
25

26. > (fibo-rec 5)
>(fibo-rec 5)
> (fibo-rec 4)
> >(fibo-rec 3)
> > (fibo-rec 2)
> > >(fibo-rec 1) To calculate (fibo 5) we calculated:
< < <1
> > >(fibo-rec 0) (fibo 4) 1 time
< < <0
<<1 (fibo 3) 2 times
> > (fibo-rec 1)
<<1 (fibo 2) 3 times
< <2
> >(fibo-rec 2) (fibo 1/0) 8 times
> > (fibo-rec 1)
<<1
> > (fibo-rec 0)
<<0
< <1
<3
> (fibo-rec 3) How many calls to calculate (fibo 60)?
> >(fibo-rec 2)
> > (fibo-rec 1)
<<1
> > (fibo-rec 0)
<<0
< <1
> >(fibo-rec 1)
< <1
<2
<5
5
26

27. Fast-Fibo Results
> (time (fibo-loop 61))
cpu time: 0 real time: 0 gc time: 0
2504730781961
2.5 Trillion applications
2.5 GHz computer does 2.5 Billion simple operations per second,
so 2.5 Trillion applications operations take ~1000 seconds.
Each application of fibo involves hundreds of simple operations…
27

28. ;;; The Earth's mass is 6.0 x 10^24 kg
> (define mass-of-earth (* 6 (expt 10 24)))
;;; A typical rabbit's mass is 2.5 kilograms
> (define mass-of-rabbit 2.5)
> (/ (* mass-of-rabbit (fibo-loop 60)) mass-of-earth)
6.450036483e-013
> (/ (* mass-of-rabbit (fibo-loop 120)) mass-of-earth)
2.2326496895795693
According to Bonacci’s model, after less than 10 years, rabbits
would out-weigh the Earth!
Beware the Bunnies!!
Beware the Sneezewort!!
28

29. The Verge of Survival
by Filip and Colton
29

30. Evaluation Cost
Actual running times How does time
vary according to:
– How fast a processor scale with the
you have size of the input?
– How much memory you
have If the input size increases by
– Where data is located in one, how much longer will it
take?
memory
– How hot it is If the input size doubles, how
– What else is running much longer will it take?
– etc...

31. Running Time of fibo-rec
Fibonacci (n) = Fibonacci(n-2) + Fibonacci(n-1)
= X Fibonacci(n-1)
= Xn
What is X?
> (exact->inexact (/ (fibo-loop 2) (fibo-loop 1)))
1.0
> (exact->inexact (/ (fibo-loop 3) (fibo-loop 2)))
2.0
> (exact->inexact (/ (fibo-loop 4) (fibo-loop 3)))
1.5

32. > (for 1 50
(lambda (i) (printf "~a~n" (exact->inexact (/ (fibo-loop (+ i 1)) (fibo-loop i))))))
1.0
2.0
1.5
1.6666666666666667
1.6
1.625
1.6153846153846154
1.619047619047619
1.6176470588235294
1.6181818181818182
1.6179775280898876
1.6180555555555556
1.6180257510729614
1.6180371352785146
1.618032786885246
1.618034447821682
1.6180338134001253
…
1.618033988749895

33. Running Time of fibo-rec
Fibonacci (n) = Fibonacci(n-2) + Fibonacci(n-1)
= ? Fibonacci(n-1)
= Φn
Φ = (/ (+ 1 (sqrt 5)) 2)
“The Golden Ratio” 1.618033988749895...
> (exact->inexact (/ (fibo-loop 41) (fibo-loop 40)))
1.618033988749895

34. “Golden” Rotunda?

35. The Golden Ratio
Euclid: “extreme and
mean ratio”
Parthenon
http://www.mathsisfun.com/numbers/golden-ratio.html
Nautilus Shell
35

36. Charge
PS4 due Monday 3 October
Exam 1: out October 7, due October 12
Covers:
Problem Sets 1-4 including PS Comments
Course Book Chapters 1-6
Classes 1-18
Reading:
no reading assignment until after Exam 1, but I will
start covering things in Chapter 7-8 soon and
encourage you to read The Information, Chapters 5-7
36