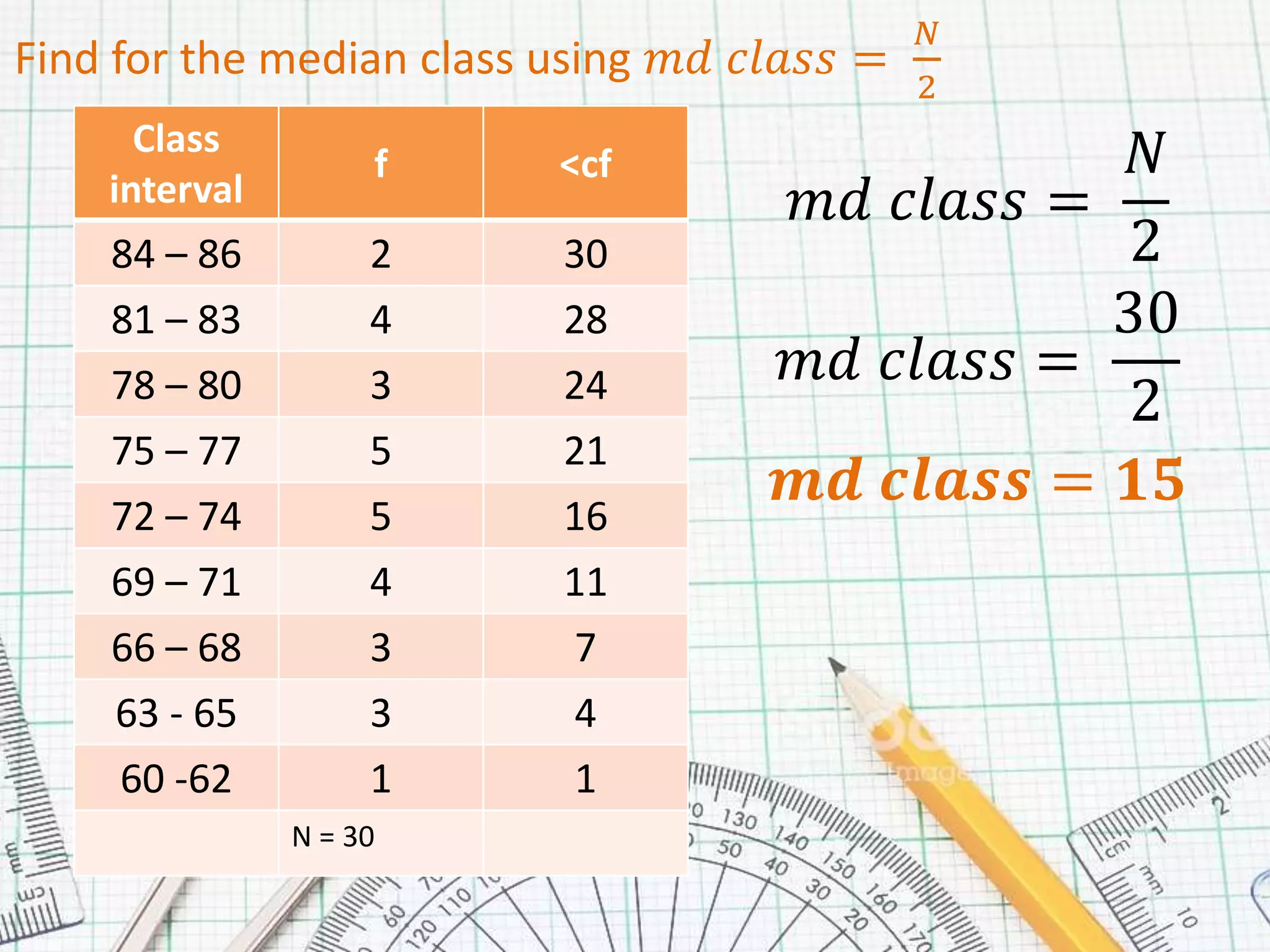
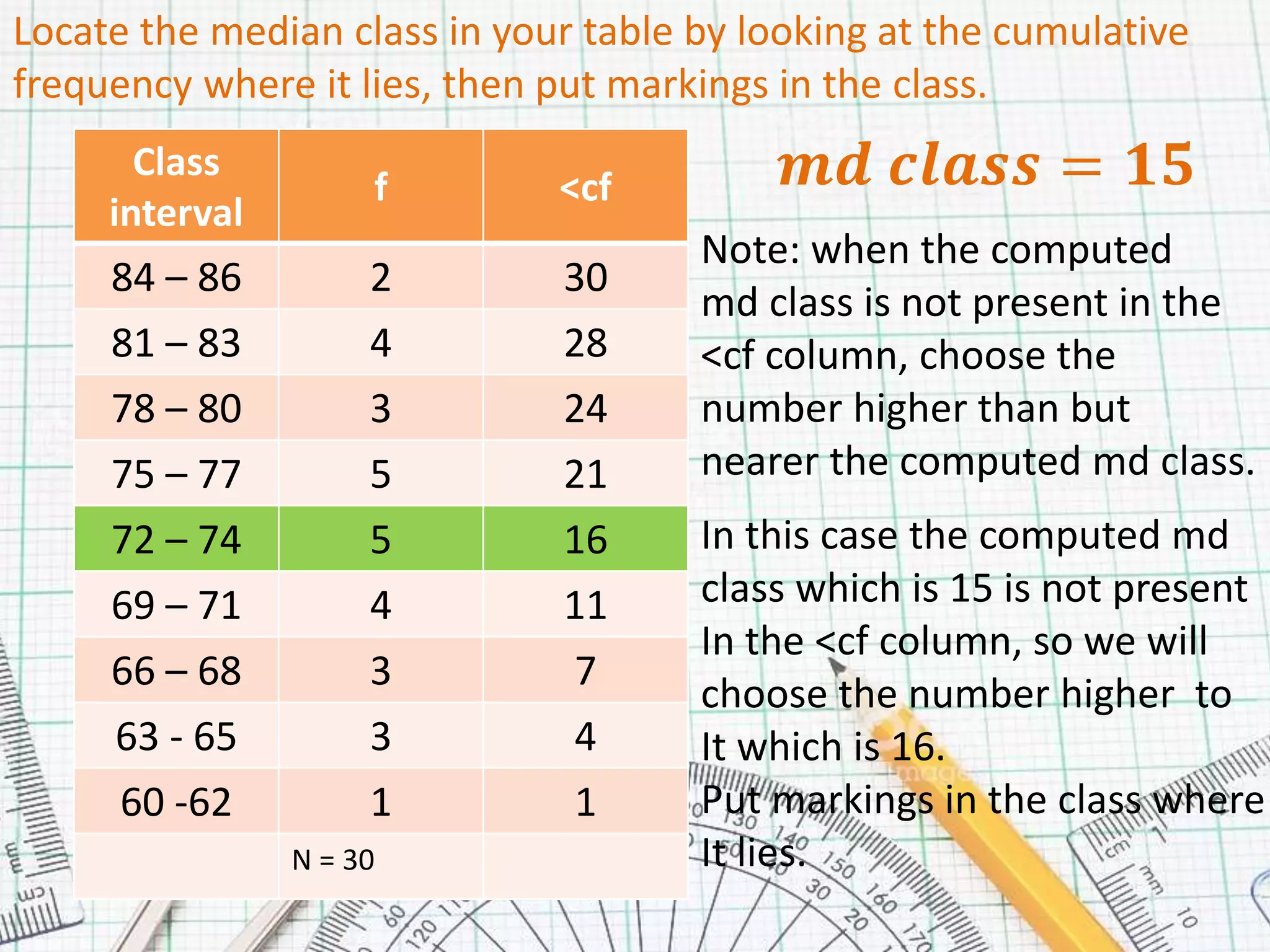
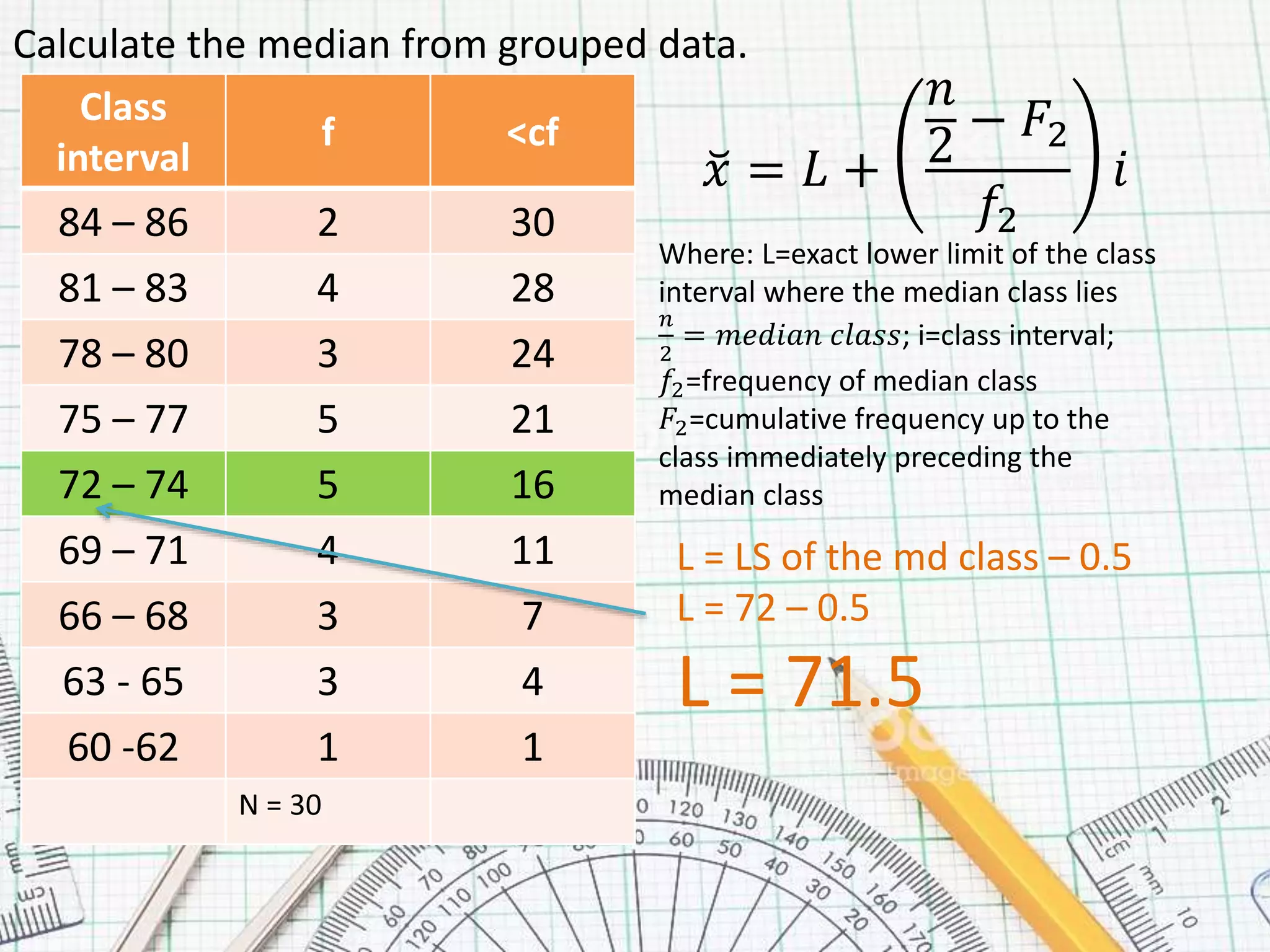
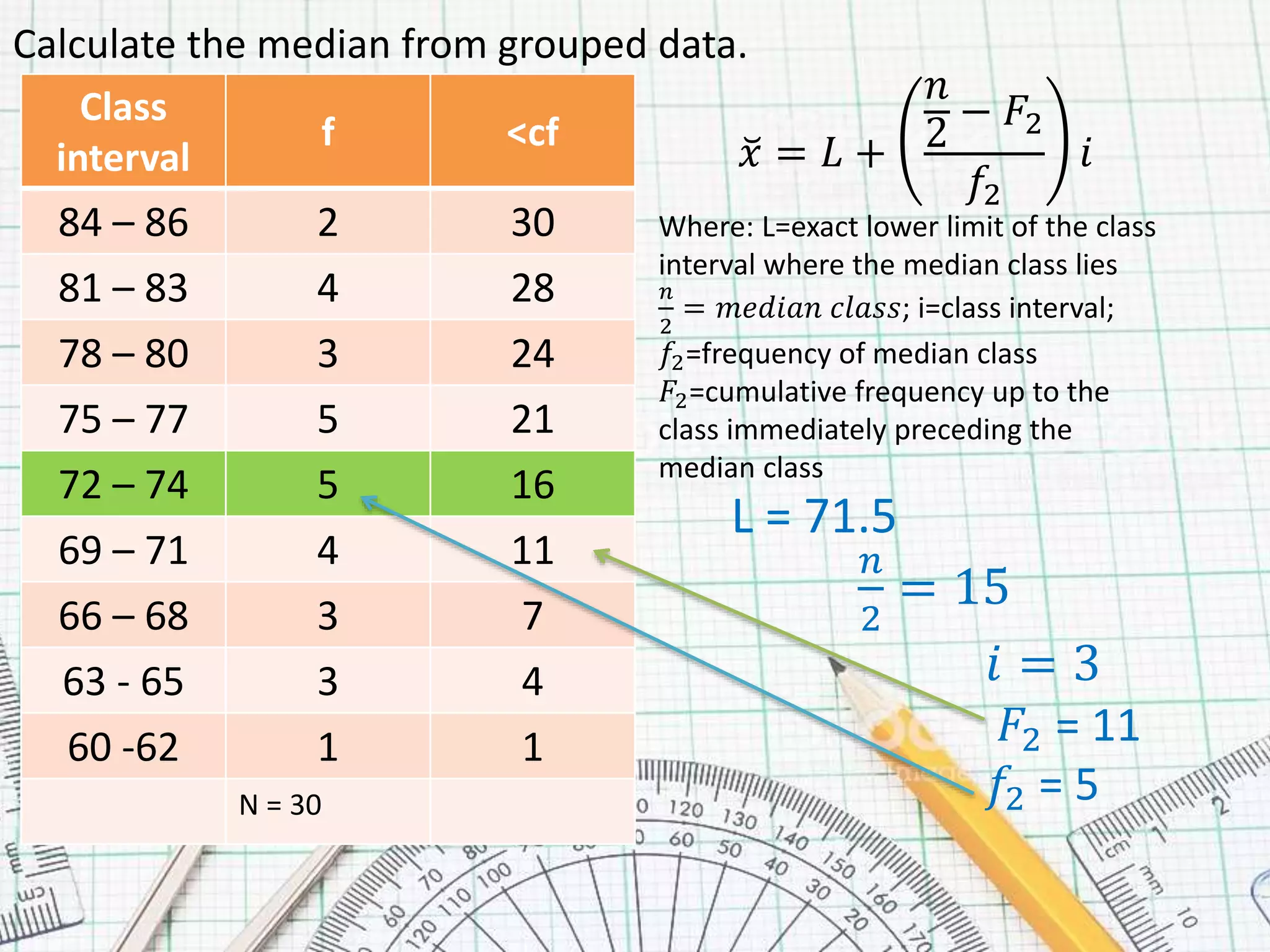
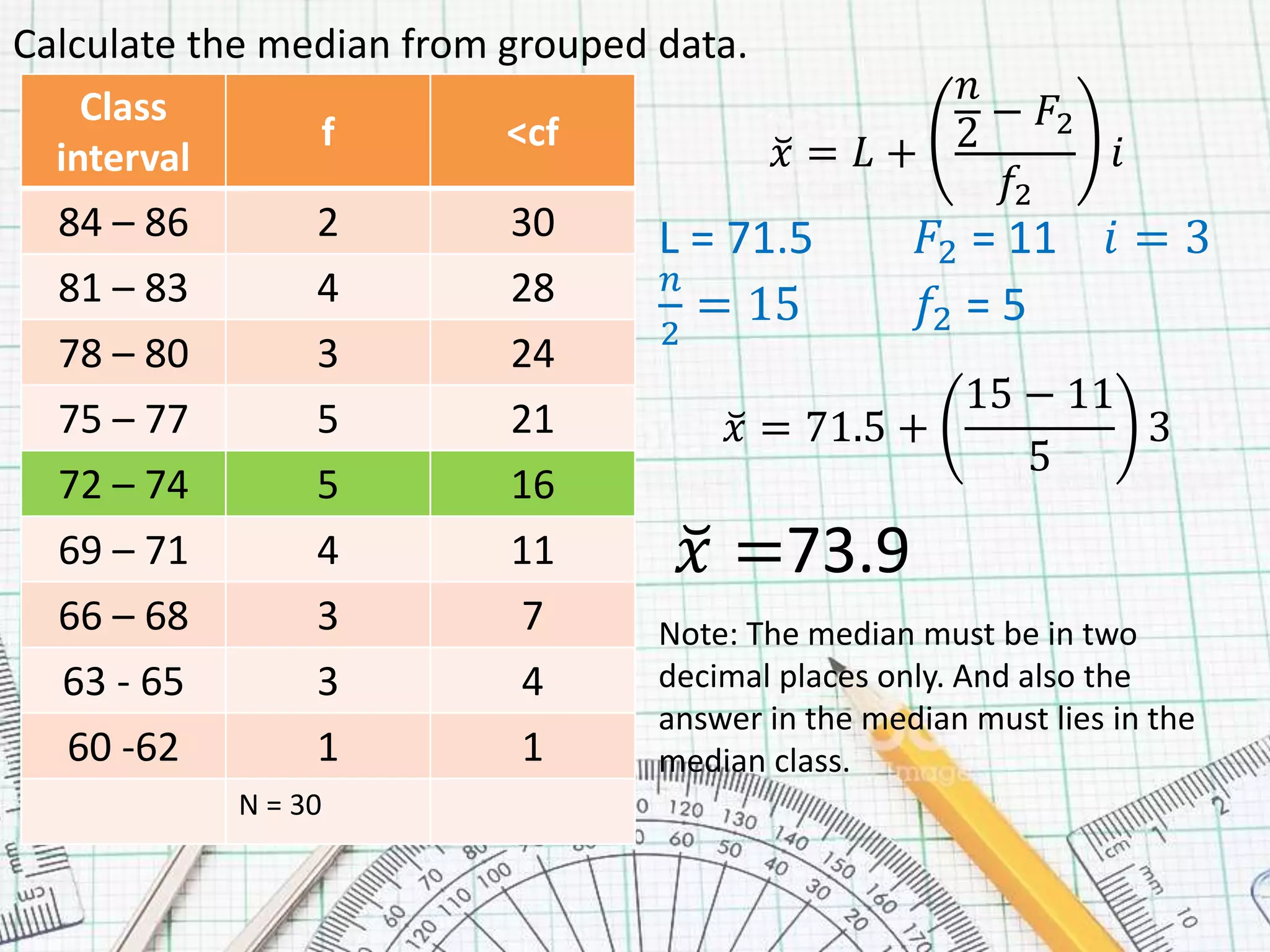
This document provides steps for calculating the median of grouped data: 1. Create a frequency distribution table with class intervals, frequencies, and cumulative frequencies. 2. Find the median class by calculating N/2, where N is the total number of data points. 3. The median is calculated using the formula: x = L + (n2 - F2)/f2 * i, where L is the lower limit of the median class, n2 is the median class, F2 is the cumulative frequency before the median class, f2 is the frequency of the median class, and i is the class interval.

1. MEDIAN of
Grouped Data
By: Maryleigh P. Castillo

2. Objectives:
• Make frequency distribution
table
• Compute for the Median

3. Steps in calculating Median of grouped data
• Make the frequency distribution table.
• Make a column for the less than cumulative frequency (<cf)
• Find for the median class using 𝑚𝑑 𝑐𝑙𝑎𝑠𝑠 =
𝑁
2
• Locate the median class in your table by looking at the
cumulative frequency where it lies, then put markings in the
class.
• Calculate the median from grouped data:
𝑥 = 𝐿 +
𝑛
2
− 𝐹2
𝑓2
𝑖
Where: L=exact lower limit of the interval where the median lies
𝑛
2
= 𝑚𝑒𝑑𝑖𝑎𝑛 𝑐𝑙𝑎𝑠𝑠; i=class interval; 𝑓2=frequency of median class
𝐹2=cumulative frequency up to the class immediately preceding the median class

4. Example:
Class interval tally frequency
84 – 86
81 – 83
78 – 80
75 – 77
72 – 74
69 – 71
66 – 68
63 - 65
60 -62
72 75 77 67 72
67 82 76 76 70
61 67 84 69 64
78 65 86 73 81
71 63 72 72 83
78 83 80 71 75

5. Make the frequency distribution table.
Class interval tally frequency
84 – 86 2
81 – 83 4
78 – 80 3
75 – 77 5
72 – 74 5
69 – 71 4
66 – 68 3
63 - 65 3
60 -62 1
N = 30

6. Make a column for the less than cumulative frequency (<cf)
Class
interval
f <cf
84 – 86 2 30
81 – 83 4 28
78 – 80 3 24
75 – 77 5 21
72 – 74 5 16
69 – 71 4 11
66 – 68 3 7
63 - 65 3 4
60 -62 1 1
N = 30
To find the cumulative frequency start
at the bottom by copying the
frequency in the lowest class interval.
Then to get the next cumulative
frequency simply add the preceding
frequency.
1 + 3 = 4
4 + 3 = 7
7 + 4 = 11

7. Find for the median class using 𝑚𝑑 𝑐𝑙𝑎𝑠𝑠 =
𝑁
2
Class
interval
f <cf
84 – 86 2 30
81 – 83 4 28
78 – 80 3 24
75 – 77 5 21
72 – 74 5 16
69 – 71 4 11
66 – 68 3 7
63 - 65 3 4
60 -62 1 1
N = 30
𝑚𝑑 𝑐𝑙𝑎𝑠𝑠 =
𝑁
2
𝑚𝑑 𝑐𝑙𝑎𝑠𝑠 =
30
2
𝒎𝒅 𝒄𝒍𝒂𝒔𝒔 = 𝟏𝟓

8. Locate the median class in your table by looking at the cumulative
frequency where it lies, then put markings in the class.
Class
interval
f <cf
84 – 86 2 30
81 – 83 4 28
78 – 80 3 24
75 – 77 5 21
72 – 74 5 16
69 – 71 4 11
66 – 68 3 7
63 - 65 3 4
60 -62 1 1
N = 30
𝒎𝒅 𝒄𝒍𝒂𝒔𝒔 = 𝟏𝟓
Note: when the computed
md class is not present in the
<cf column, choose the
number higher than but
nearer the computed md class.
In this case the computed md
class which is 15 is not present
In the <cf column, so we will
choose the number higher to
It which is 16.
Put markings in the class where
It lies.

9. Calculate the median from grouped data.
Class
interval
f <cf
84 – 86 2 30
81 – 83 4 28
78 – 80 3 24
75 – 77 5 21
72 – 74 5 16
69 – 71 4 11
66 – 68 3 7
63 - 65 3 4
60 -62 1 1
N = 30
𝑥 = 𝐿 +
𝑛
2
− 𝐹2
𝑓2
𝑖
Where: L=exact lower limit of the class
interval where the median class lies
𝑛
2
= 𝑚𝑒𝑑𝑖𝑎𝑛 𝑐𝑙𝑎𝑠𝑠; i=class interval;
𝑓2=frequency of median class
𝐹2=cumulative frequency up to the
class immediately preceding the
median class
L = LS of the md class – 0.5
L = 72 – 0.5
L = 71.5

10. Calculate the median from grouped data.
Class
interval
f <cf
84 – 86 2 30
81 – 83 4 28
78 – 80 3 24
75 – 77 5 21
72 – 74 5 16
69 – 71 4 11
66 – 68 3 7
63 - 65 3 4
60 -62 1 1
N = 30
𝑥 = 𝐿 +
𝑛
2
− 𝐹2
𝑓2
𝑖
Where: L=exact lower limit of the class
interval where the median class lies
𝑛
2
= 𝑚𝑒𝑑𝑖𝑎𝑛 𝑐𝑙𝑎𝑠𝑠; i=class interval;
𝑓2=frequency of median class
𝐹2=cumulative frequency up to the
class immediately preceding the
median class
L = 71.5
𝑛
2
= 15
𝑖 = 3
𝐹2 = 11
𝑓2 = 5

11. Calculate the median from grouped data.
Class
interval
f <cf
84 – 86 2 30
81 – 83 4 28
78 – 80 3 24
75 – 77 5 21
72 – 74 5 16
69 – 71 4 11
66 – 68 3 7
63 - 65 3 4
60 -62 1 1
N = 30
𝑥 = 𝐿 +
𝑛
2
− 𝐹2
𝑓2
𝑖
L = 71.5 𝐹2 = 11 𝑖 = 3
𝑛
2
= 15 𝑓2 = 5
𝑥 = 71.5 +
15 − 11
5
3
𝑥 =73.9
Note: The median must be in two
decimal places only. And also the
answer in the median must lies in the
median class.