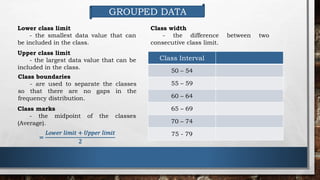
- A frequency distribution organizes data into classes and displays the frequency of observations in each class. - Grouped data uses classes with cut-offs to group interval or ratio level data, while ungrouped data lists each observation individually for smaller data sets. - To make a frequency distribution, the data's range is found and classes are determined. Each observation is tallied and frequencies per class are calculated. This displays the distribution of the data.

2. FREQUENCY DISTRIBUTION
• A frequency distribution is a way of presenting and
organizing the data collected in tabular from using classes
and frequencies.
GROUPED DATA UNGROUPED DATA
• Grouped Data are organized and
arrange into different classes and
categories.
• Having an interval or ratio – level
data, and beyond a sample size of
30.
• Frequencies of each data point are
clustered in a specific class
interval.
• Ungrouped Data are recorded as
they occur, as they come, or as
they happen.
• Classifies a given data set (usually
n≤30) under a specific category or
class.
• Frequencies of each data is treated
as individual data points or as
discrete data.

3. FREQUENCY DISTRIBUTION TABLE
A frequency distribution table shows
the data arrange into different classes
and the number of cases that fall into
each class. Frequency is the number of
times a certain value or class of values
occurs.

4. UNGROUPED DATA GROUPED DATA
SCORE TALLY FREQUENCY
3
4
5
6
7
8
9
10
SCORE FREQUENCY
60-64
65-69
70-74
75-79
80-84
85-89
90-94
95-99

5. UNGROUPED DATA
Example:
The scores of twenty grade 7 students in a 10-items math quiz are as
follows:
3 10 6 8 8 9 5 3 6 7
7 9 6 7 8 7 4 5 7 6

6. Step 1:
Construct a table with three columns. The first column shows
what is being arranged in ascending order.
SCORE TALLY FREQUENCY
3
4
5
6
7
8
9
10
3 10 6 8 8 9 5 3 6 7
7 9 6 7 8 7 4 5 7 6
3 10

7. Step 2:
Go through the list of scores. The score in the list is 3, so put a
tally mark or a thick mark at 3 in the second column.
SCORE TALLY FREQUENCY
3
4
5
6
7
8
9
10
3 10 6 8 8 9 5 3 6 7
7 9 6 7 8 7 4 5 7 6

8. Step 3:
Count the number of tally marks for each score and write it in third
column. The finished frequency table is as follows:
SCORE TALLY FREQUENCY
3 II
4 I
5 II
6 IIII
7 IIIII
8 III
9 II
10 I
Total
2
1
4
2
5
3
2
1
n = 20

9. Example 2:
Twenty-five positive cases of Covid-19 were given a blood test to
determine their blood type. The data sets is as follows:
A B B AB O
O O B AB B
B B O A O
A O O O AB
AB A O B A

10. BLOOD TYPE TALLY FREQUENCY
A
B
O
AB
Total
A B B AB O
O O B AB B
B B O A O
A O O O AB
AB A O B A
5
4
9
7
n = 25

11. GROUPED DATA
Lower class limit
- the smallest data value that can
be included in the class.
Upper class limit
- the largest data value that can be
included in the class.
Class boundaries
- are used to separate the classes
so that there are no gaps in the
frequency distribution.
Class marks
- the midpoint of the classes
(Average).
Class width
- the difference between two
consecutive class limit.
Class Interval
50 – 54
55 – 59
60 – 64
65 – 69
70 – 74
75 - 79

12. Example 1.
Construct a frequency distribution table given the set of data using 6 classes.
Score of 40 Students in math
quiz
86 83 81 81
86 91 79 82
81 87 87 83
82 72 73 78
87 70 90 75
80 82 89 98
89 80 96 76
99 71 88 85
82 90 91 94
72 83 74 85
Step 1. Find the range. = HN – LN
= 99 – 70
= 29

13. Example 1.
Construct a frequency distribution table given the set of data
using 6 classes.
Score of 40 Students in math quiz
86 83 81 81
86 91 79 82
81 87 87 83
82 72 73 78
87 70 90 75
80 82 89 98
89 80 96 76
99 71 88 85
82 90 91 94
72 83 74 85
Step 2. Decide on the number of
classes.
= 6
2𝑘 > 𝑛
Where k = unknown number ; n = total
number of correspondent

14. Example 1.
Construct a frequency distribution table given the set of data using 6
classes.
Score of 40 Students in math quiz
86 83 81 81
86 91 79 82
81 87 87 83
82 72 73 78
87 70 90 75
80 82 89 98
89 80 96 76
99 71 88 85
82 90 91 94
72 83 74 85
range = 29 No. of classes = 6
Step 3. Find the class width. Divide the
range by the number of classes.
Class width =
𝑟𝑎𝑛𝑔𝑒
𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑐𝑙𝑎𝑠𝑠𝑒𝑠
=
29
6
= 4.833… = 5

15. Example 1.
Construct a frequency distribution table given the set of data using 6
classes.
Score of 40 Students in math quiz
86 83 81 81
86 91 79 82
81 87 87 83
82 72 73 78
87 70 90 75
80 82 89 98
89 80 96 76
99 71 88 85
82 90 91 94
72 83 74 85
Step 4 : Add the ‘class width’ to the
starting point to get the second lower
class limit. Then enter the upper class
limit.
Step 5 : Represent each score by a tally
count the total frequency of each class.

16. Example 1.
Construct a frequency distribution table given the set of data using 6
classes.
Score of 40 Students in math quiz
86 83 81 81
86 91 79 82
81 87 87 83
82 72 73 78
87 70 90 75
80 82 89 98
89 80 96 76
99 71 88 85
82 90 91 94
72 83 74 85
Class Interval Tally Frequency
70 – 74 3
75 – 79 5
80 – 84 9
85 – 89 13
90 – 94 4
95 - 99 6
No. of classes = 6 Class width = 5

17. Class Interval Tally Frequency (f) Class
boundaries
Class mark
70 – 74 3 69.5 – 74.5 72
75 – 79 5 74.5 – 79.5 77
80 – 84 9 79.5 – 84.5 82
85 – 89 13 84.5 – 89.5 87
90 – 94 4 89.5 – 94.5 92
95 - 99 6 94.5 – 99.5 97
Example 1.
Construct a frequency distribution table given the set of data using 6
classes.
n = 40 =
70+74
2
=
144
2
= 72