Downloaded 104 times
Uploaded byLiwayway Memije-Cruz
Graph: Euler path and Euler circuit
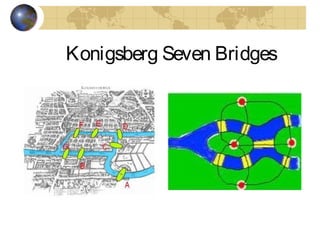
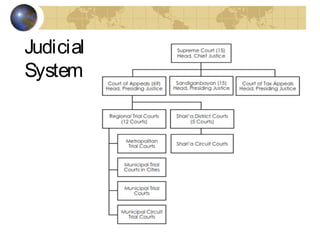
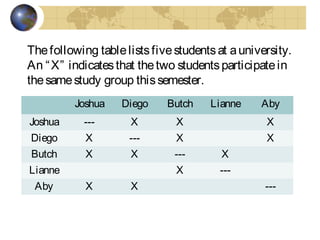
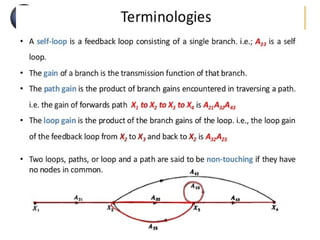
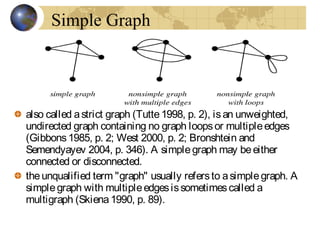
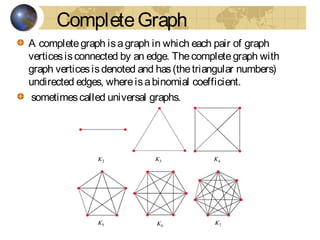
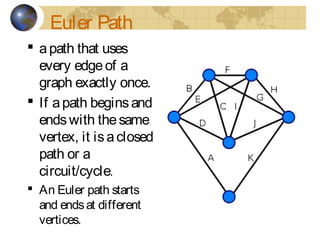
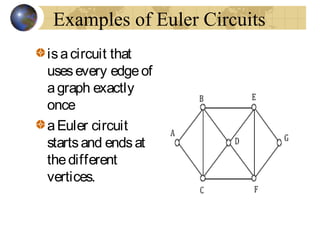
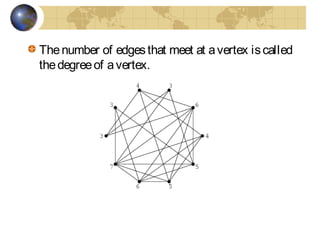
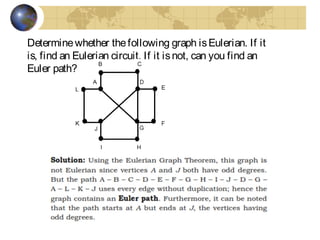
This document discusses graphs and Euler paths/circuits. It defines what a graph is - a collection of vertices connected by edges. An Euler path uses every edge once, starting and ending at different vertices. An Euler circuit is a closed path that uses every edge once, starting and ending at the same vertex. The Euler theorem states that a connected graph has an Euler circuit if every vertex has an even degree. The document provides examples of Euler paths and circuits and applications to problems like planning a bike route that uses every trail once.
More Related Content
Similar to Graph: Euler path and Euler circuit
More from Liwayway Memije-Cruz
Graph: Euler path and Euler circuit
- 1. Graph: Euler Pathand Euler Circuit By Prof. Liwayway Memije-Cruz
- 2.
- 3. A graph isa diagram displaying data; showing the relationship between two or more quantities, measurements or indicative numbers that may or may not have a specific mathematical formula relating them to each other.
- 4. What is aGraph? acollection of pointscalled verticesor nodes, and connecting segmentscalled edges. sometimestheedgesaregiven orientationsand arerepresented by arrowsor aregiven values (weights). theposition of thevertices, thelengthsof the edges, and theshapeof theedgesdo not matter in agraph. What welook at isthenumber of verticesand which of them arejoined by edges.
- 5.
- 6. The graph indicates the socialnetwork of neurological patients.
- 7.
- 8.
- 9.
- 10.
- 11. Thefollowing tablelistsfivestudentsat auniversity. An“X” indicatesthat thetwo studentsparticipatein thesamestudy group thissemester. Joshua Diego Butch Lianne Aby Joshua --- X X X Diego X --- X X Butch X X --- X Lianne X --- Aby X X ---
- 12. Draw a graphthat represents this information where each vertex represents a student and an edge connects two vertices if the corresponding students study together.
- 14. Simple Graph also calledastrict graph (Tutte1998, p. 2), isan unweighted, undirected graph containing no graph loopsor multipleedges (Gibbons1985, p. 2; West 2000, p. 2; Bronshtein and Semendyayev 2004, p. 346). A simplegraph may beeither connected or disconnected. theunqualified term "graph" usually refersto asimplegraph. A simplegraph with multipleedgesissometimescalled a multigraph (Skiena1990, p. 89).
- 15. A graph isconnectedif thereisapath connecting all thevertices. Two verticesareadjacent if thereisan edge joining them. If every pair of verticesof agraph are adjacent, thegraph iscomplete. A completegraph with n verticesisdenoted by Kn. Thedegreeof avertex isthenumber of edges attached to it.
- 16. CompleteGraph A completegraph isagraphin which each pair of graph verticesisconnected by an edge. Thecompletegraph with graph verticesisdenoted and has(thetriangular numbers) undirected edges, whereisabinomial coefficient. sometimescalled universal graphs.
- 17.
- 18. Euler Path apaththat uses every edgeof a graph exactly once. If apath beginsand endswith thesame vertex, it isaclosed path or a circuit/cycle. An Euler path starts and endsat different vertices.
- 19. Leonard Euler A Swissmathematicianand physicist, oneof thefoundersof puremathematics. Henot only madedecisiveand formativecontributionsto the subjectsof geometry, calculus, mechanics, and number theory but also developed methodsfor solving problemsin observational astronomy and demonstrated useful applications of mathematicsin technology and public affairs.
- 20. Examples of EulerCircuits isacircuit that usesevery edgeof agraph exactly once aEuler circuit startsand endsat thedifferent vertices.
- 21. Thenumber of edgesthatmeet at avertex iscalled thedegreeof avertex.
- 22. Eulerian Graph Theorem Aconnected graph isEulerian if and only if each vertex of thegraph isof even degree. Eulerian Graph Theorem only guaranteesthat if thedegreesof all the verticesin agraph areeven, an Euler circuit exists, but it doesnot tell ushow to find one.
- 23. Determinewhether thegraph belowisEulerian. If it is, find an Euler circuit. If it isnot, explain why.
- 24. Determinewhether thefollowing graphisEulerian. If it is, find an Eulerian circuit. If it isnot, can you find an Euler path?
- 25. Euler Path Theorem •A connected graph containsan Euler path if and only if thegraph hastwo verticesof odd degreewith all other verticesof even degree. • Every Euler path must start at oneof the verticesof odd degreeand end at theother.
- 26.
- 27. Application of EulerPath Theorem Below isthemap of all the trailsin anational park. A biker would liketo traverseall thetrailsexactly once. Isit possiblefor thebiker to plan atrip that traversesall thetrailsexactly once? Isit possiblefor him to traverseall thetrailsand return to thestarting point without repeating any trail in the trip?
- 28.