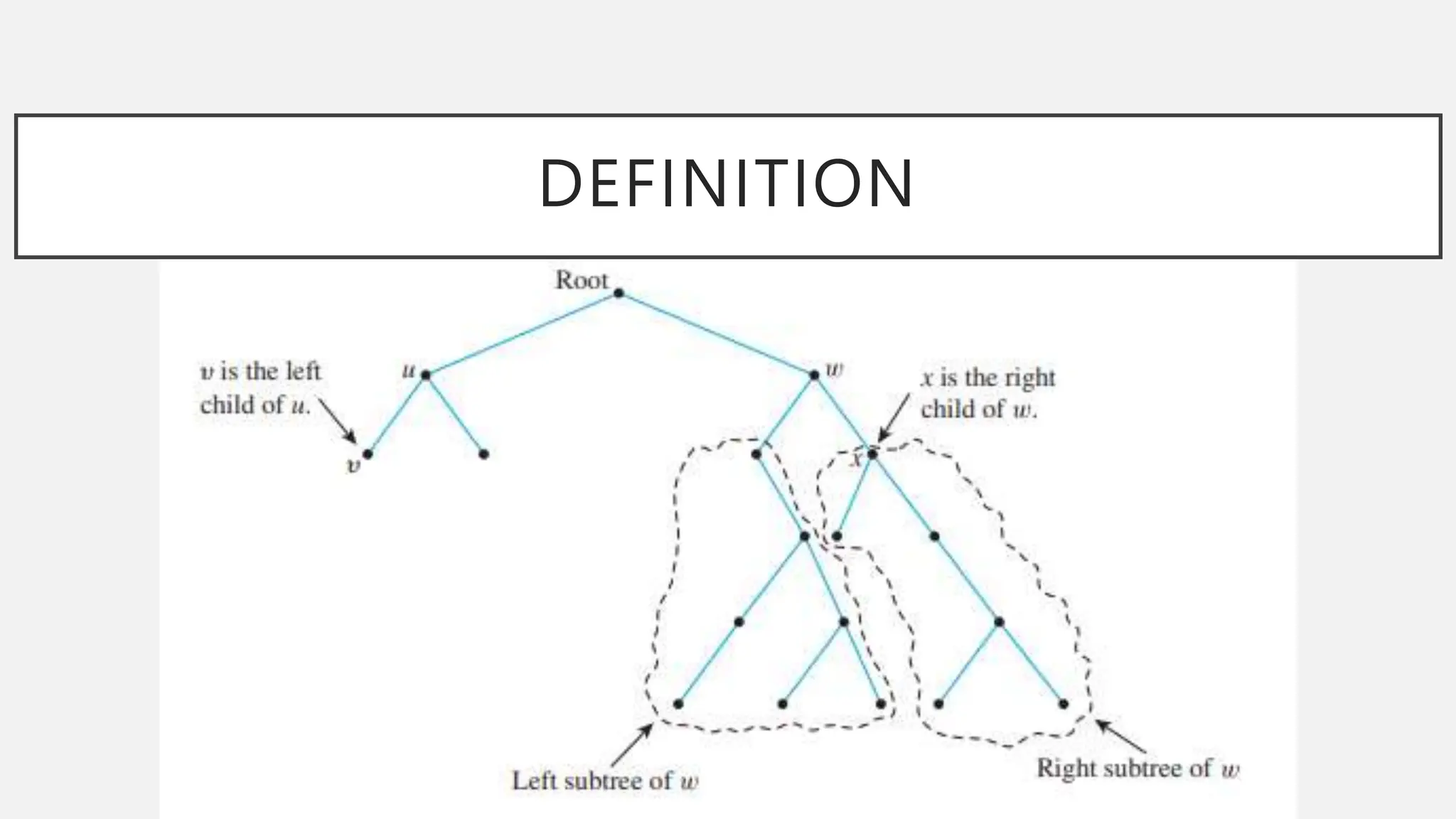
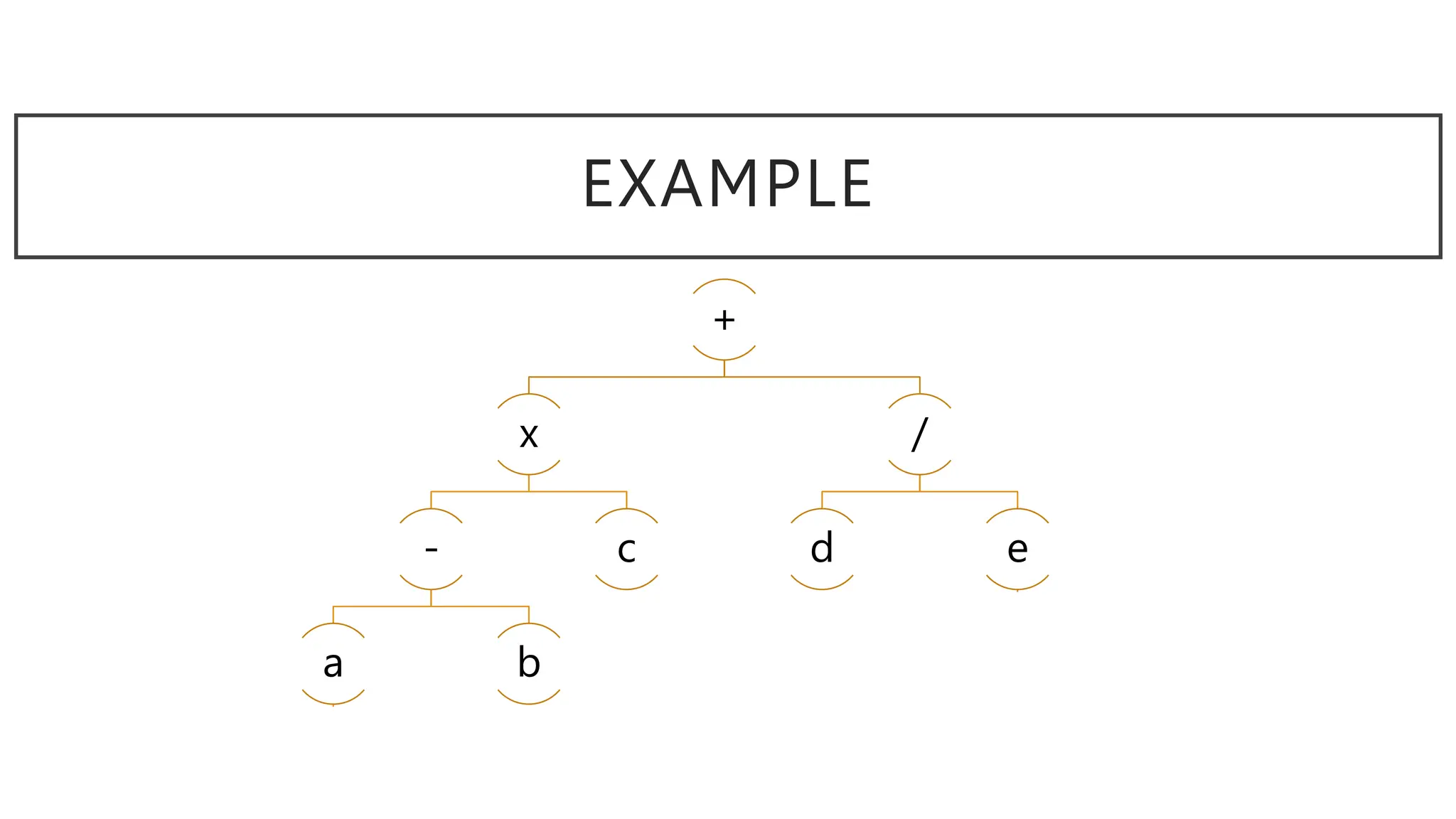
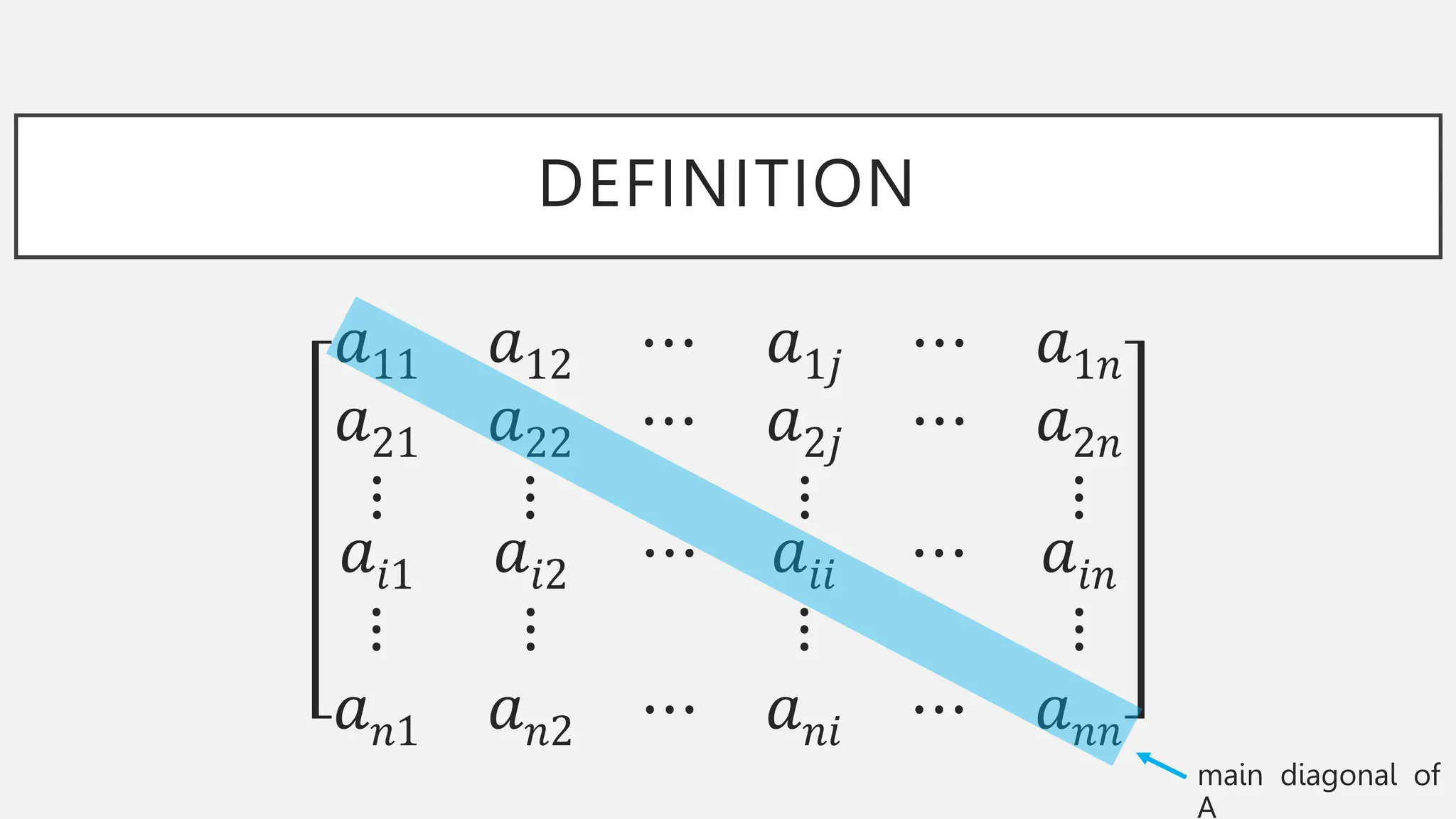
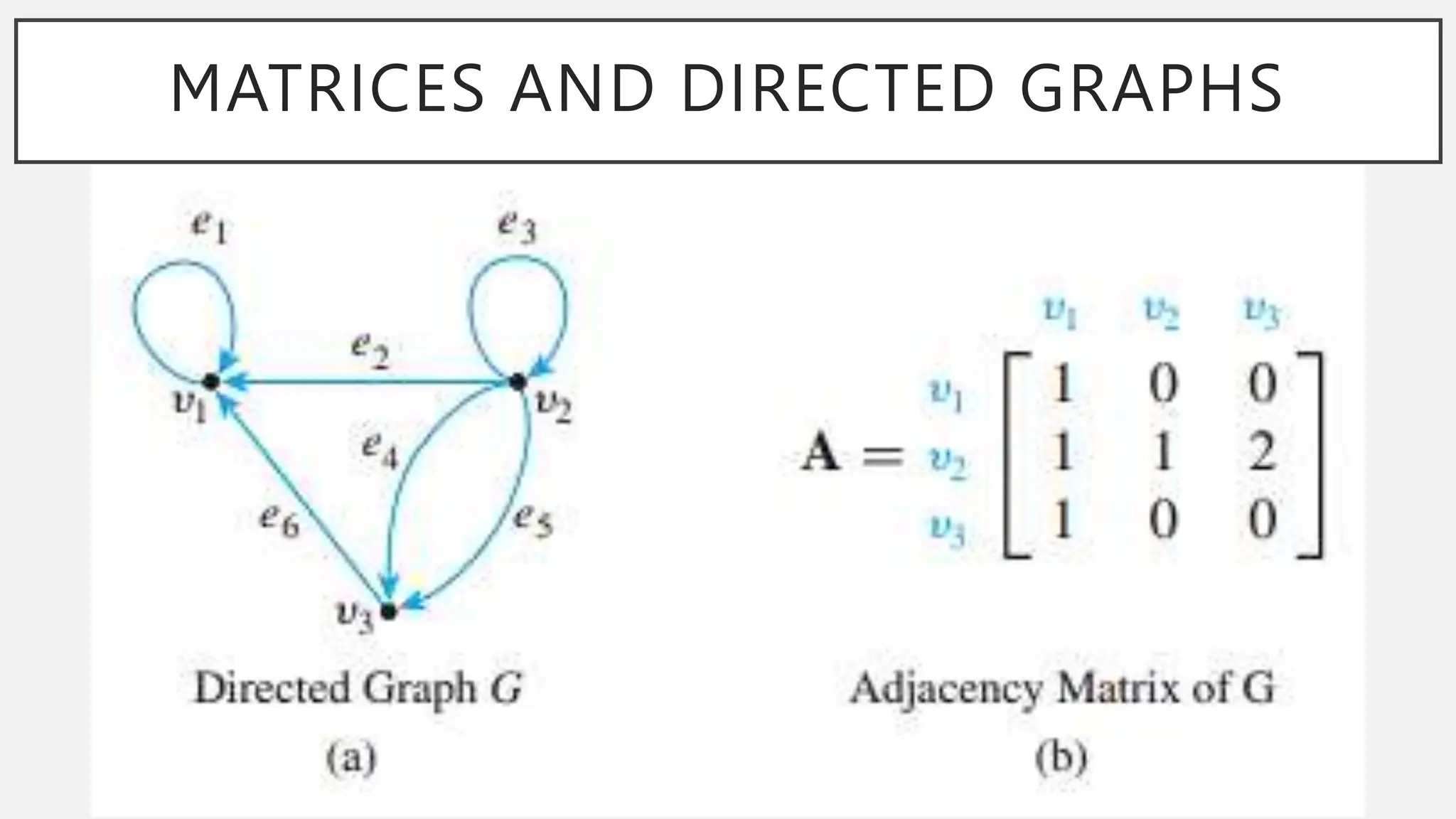
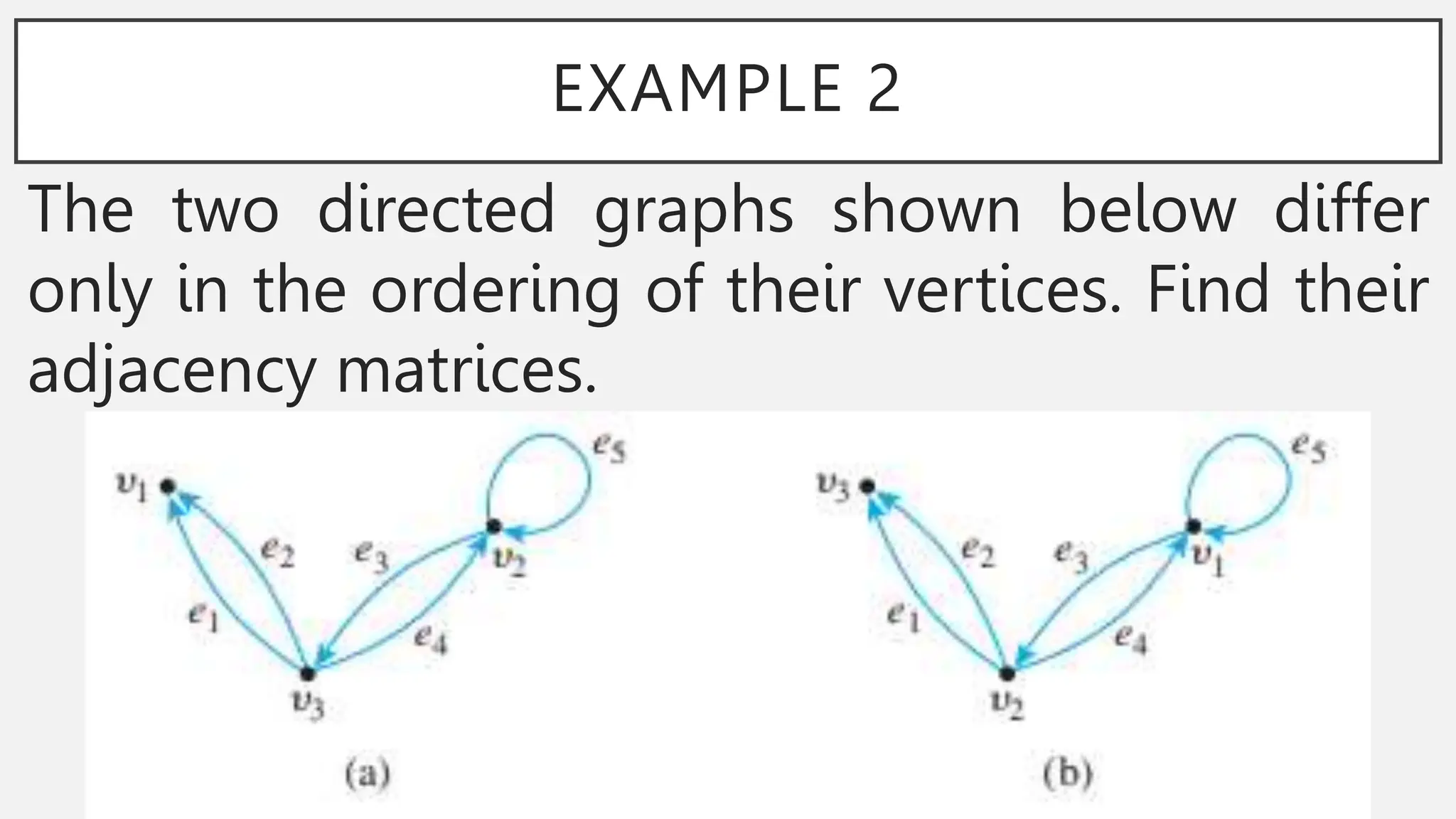
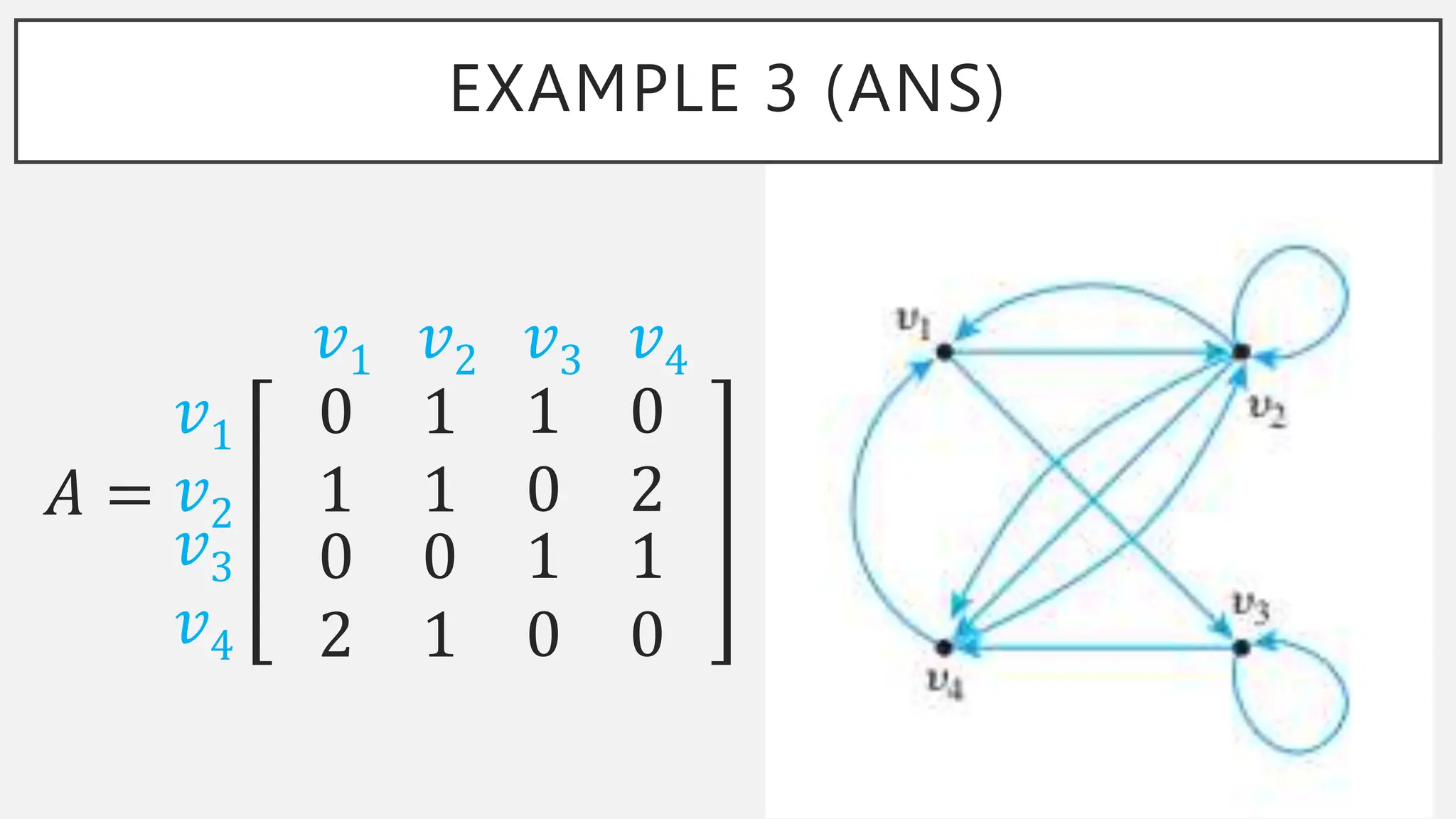
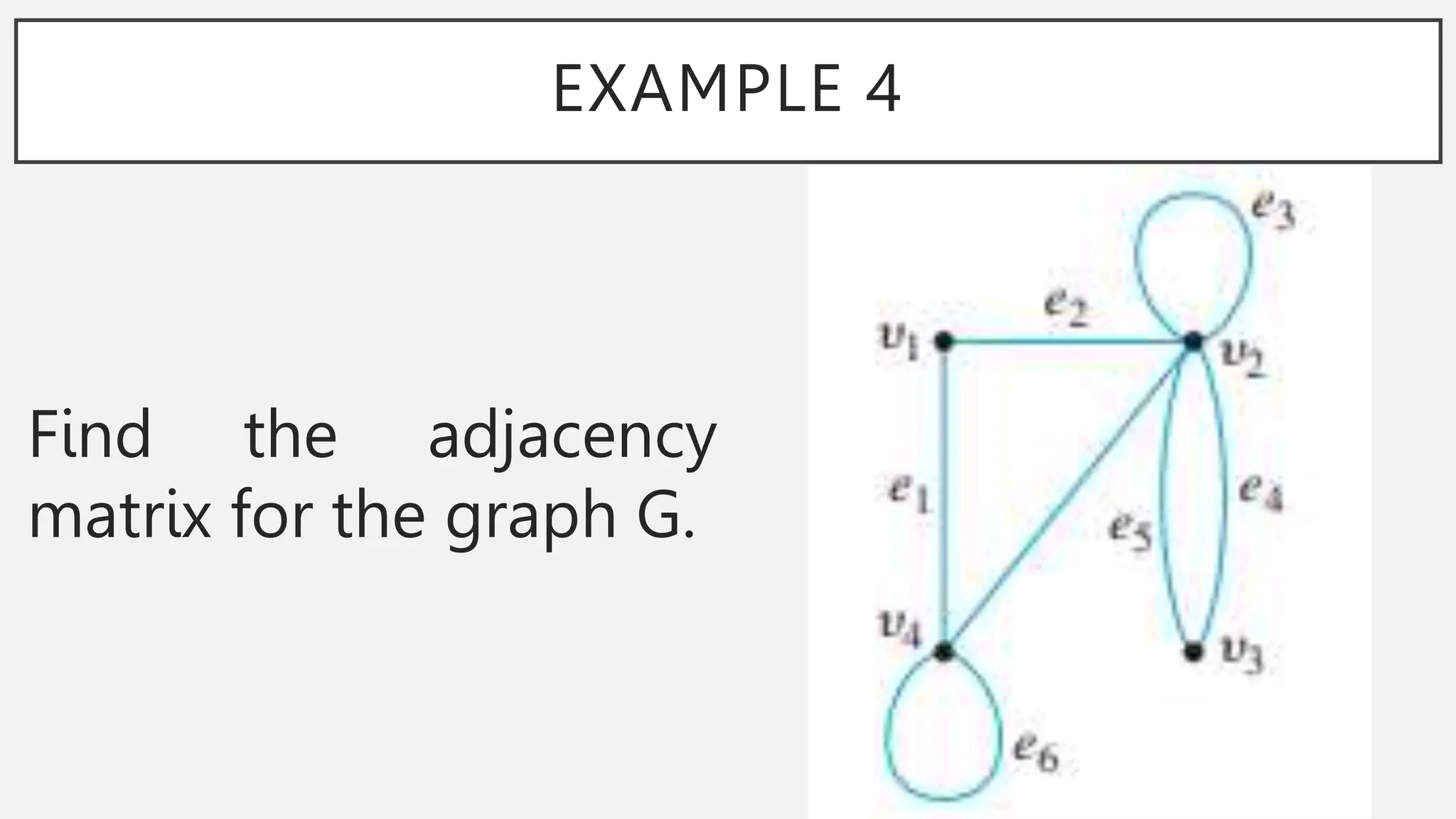
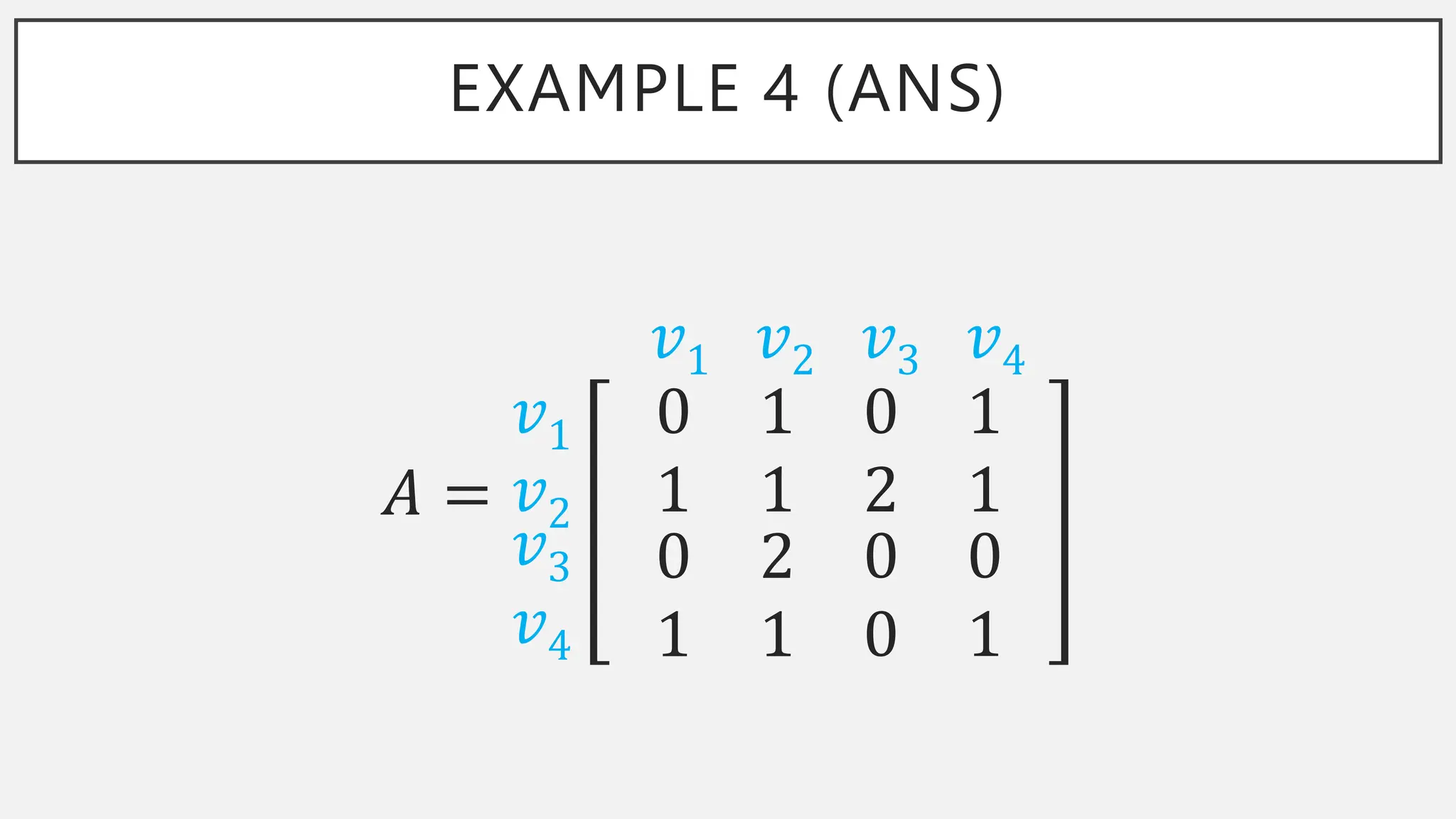
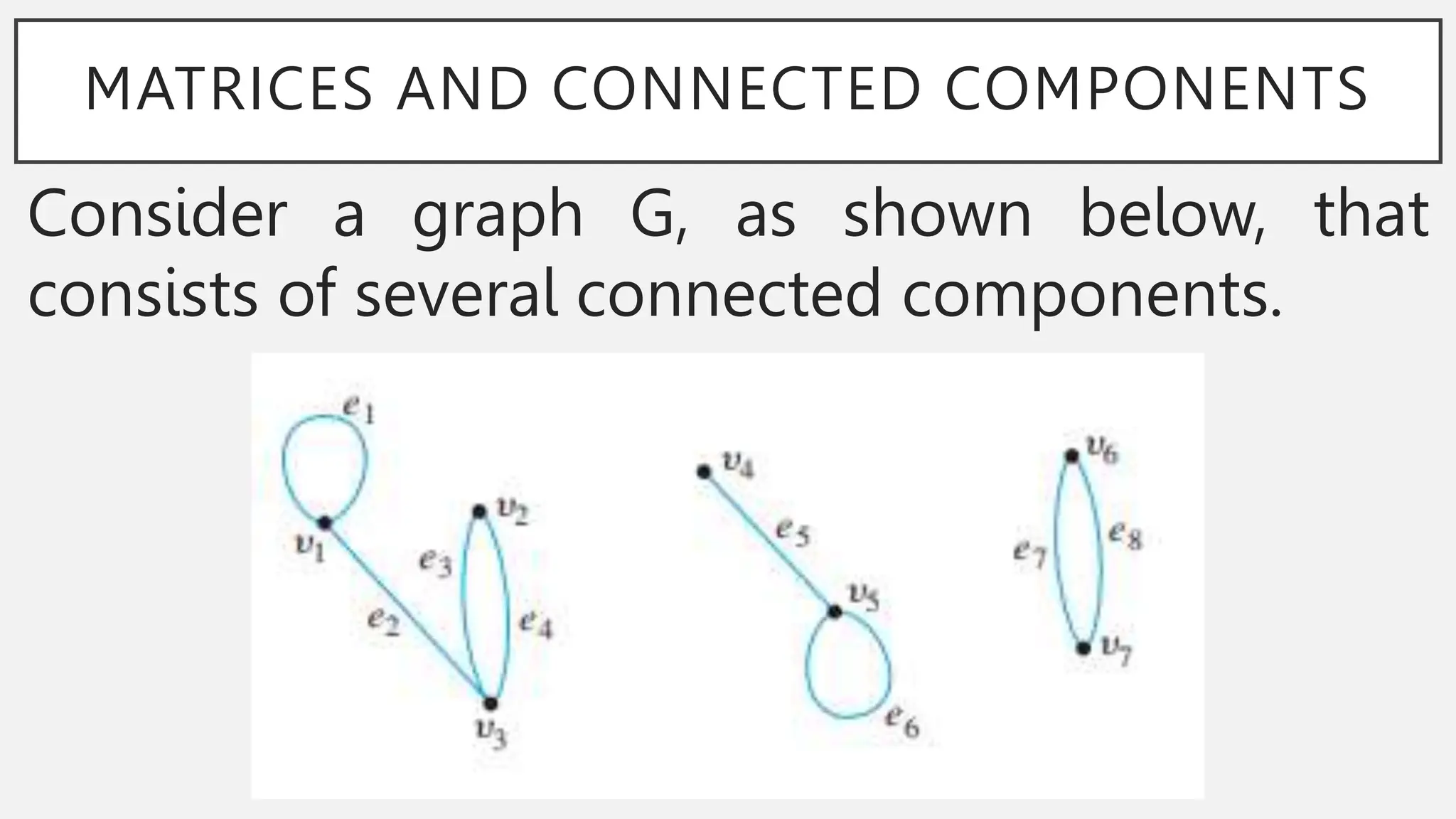
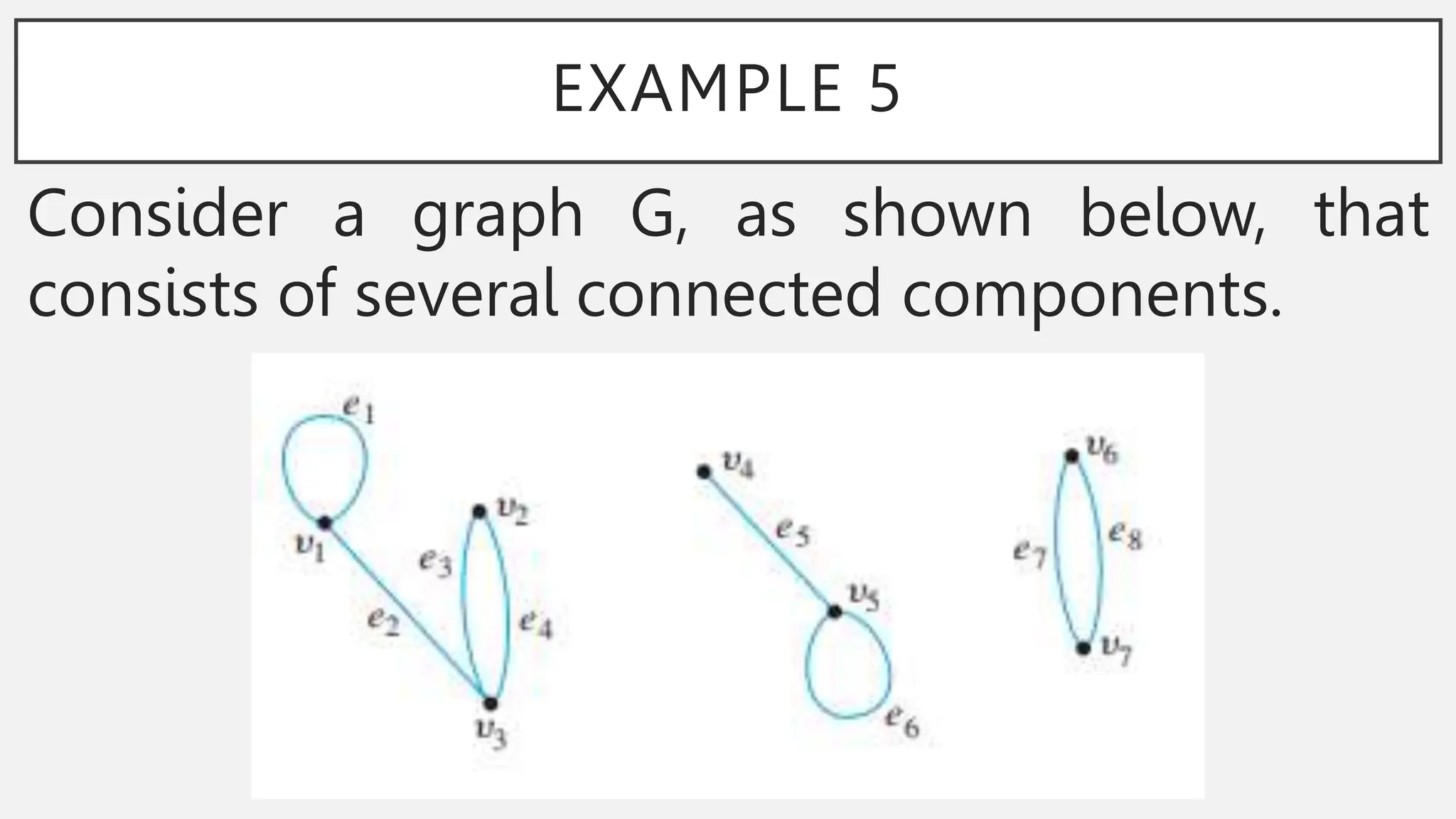
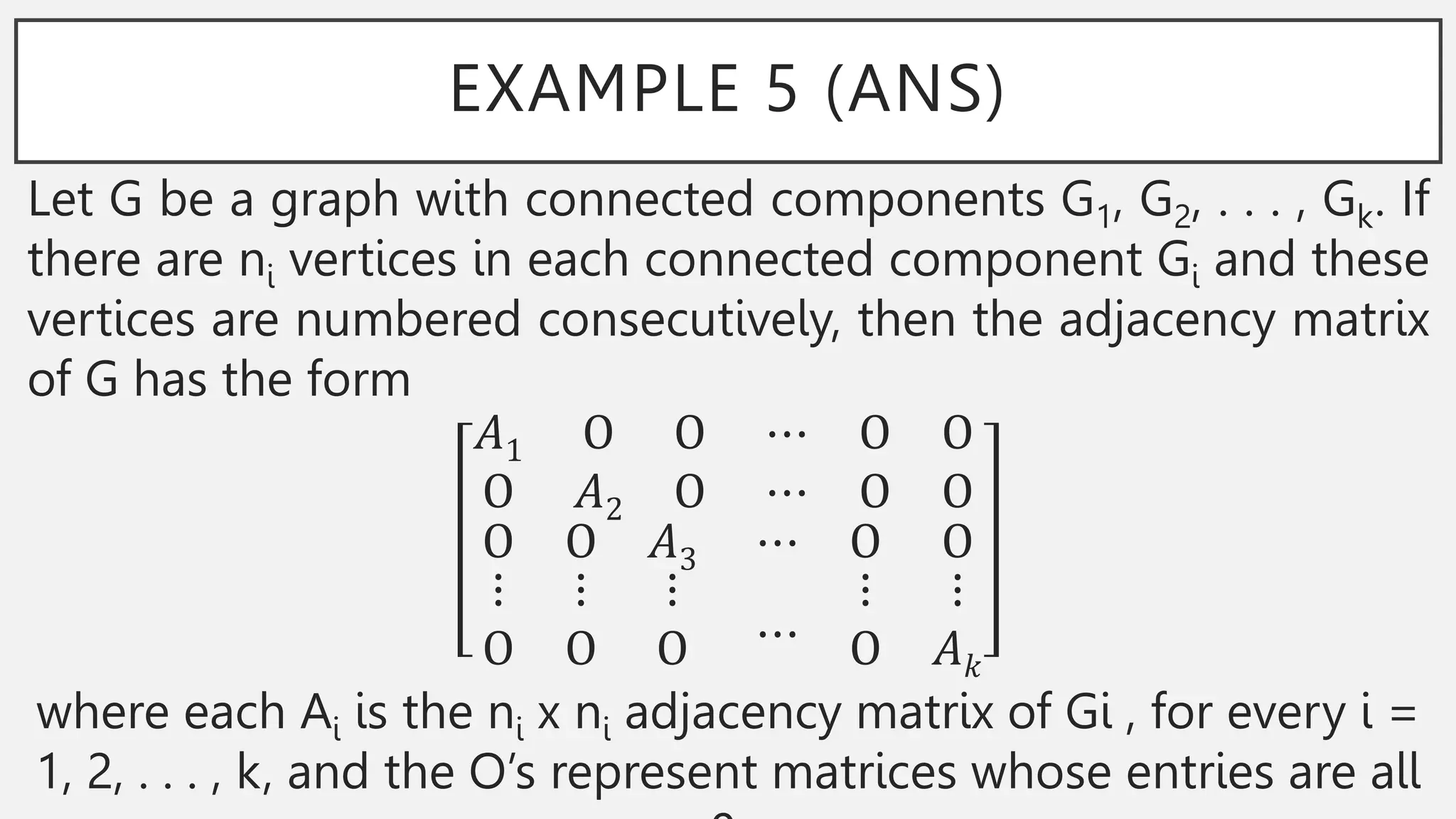
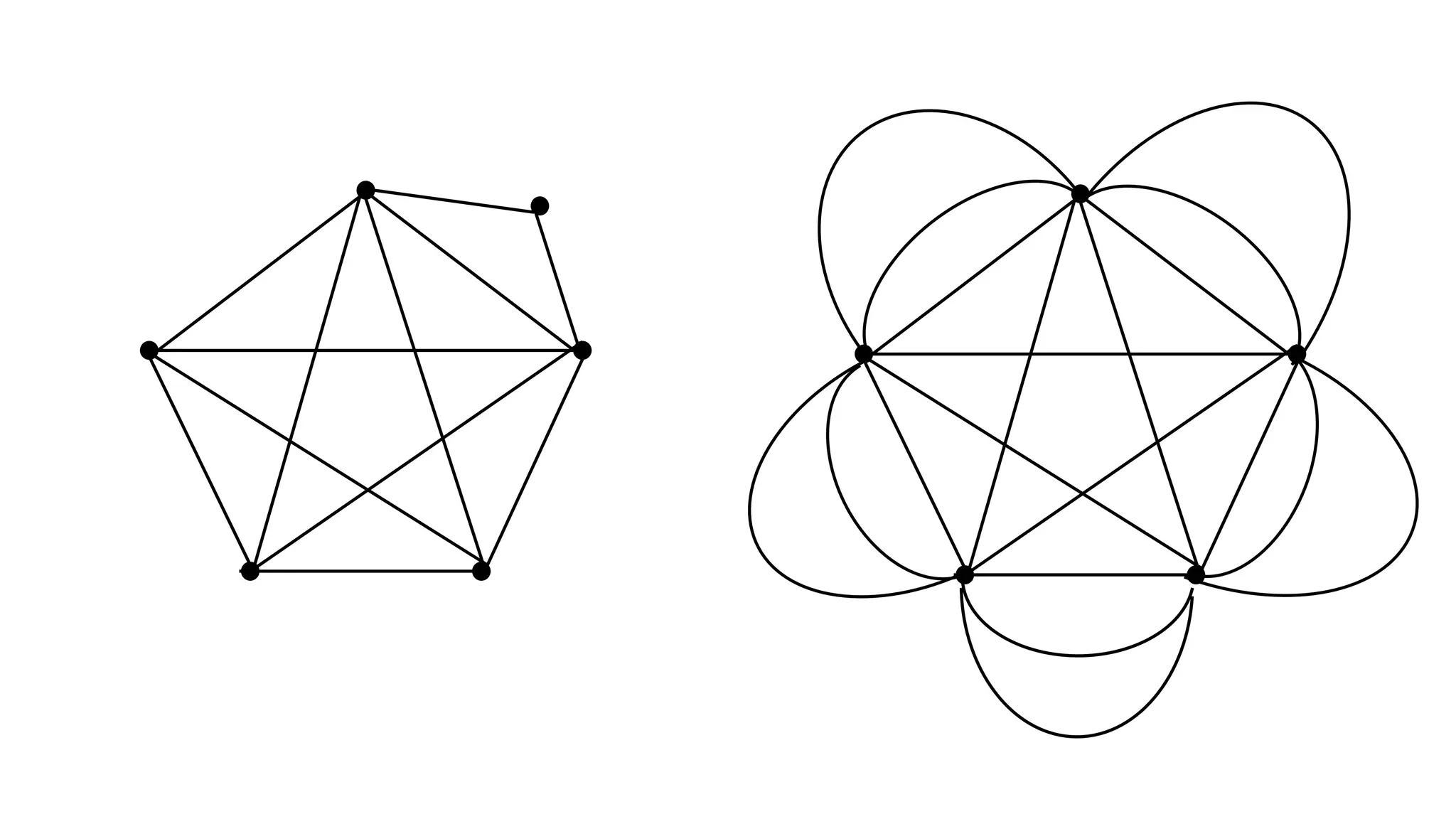
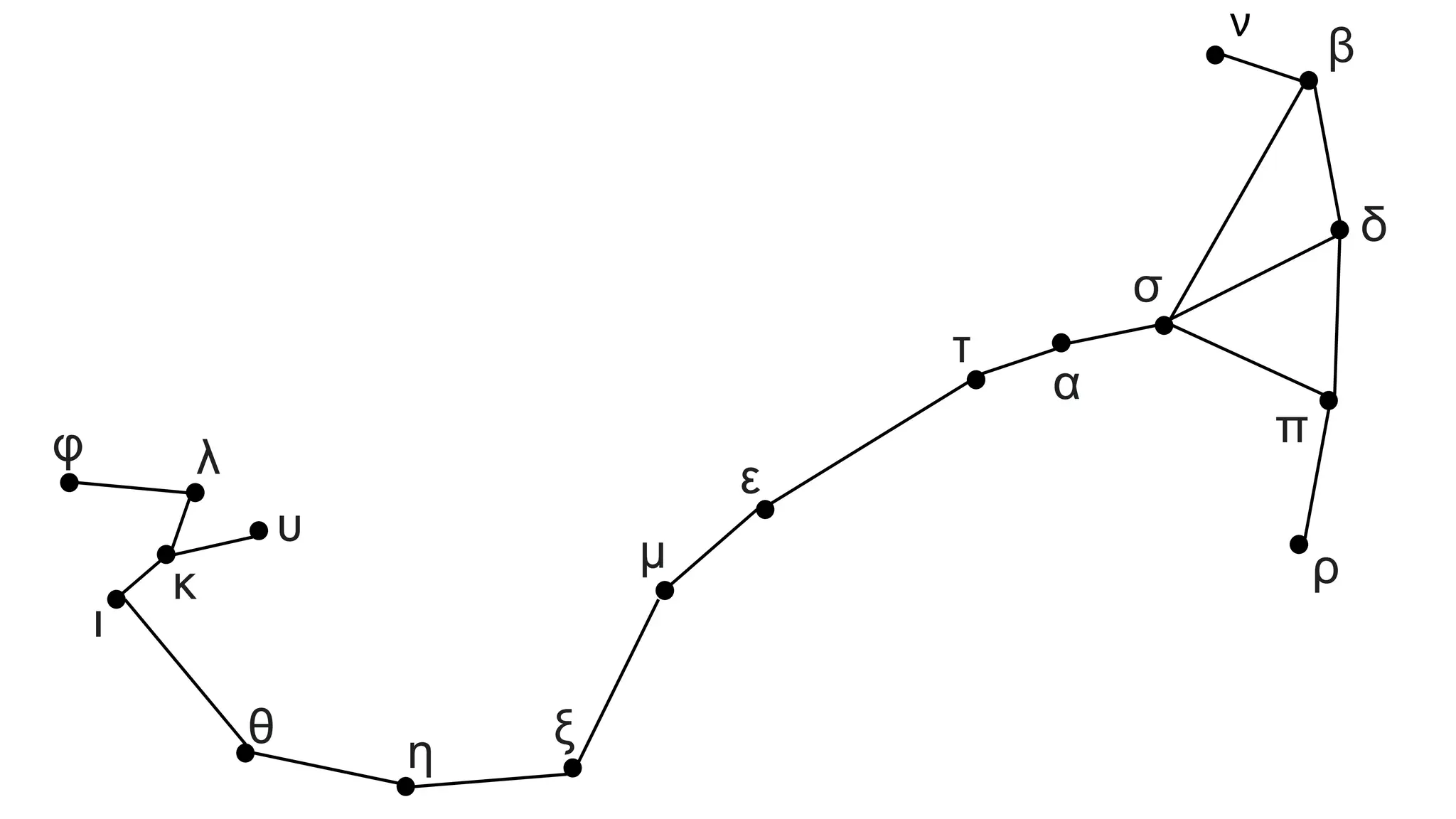
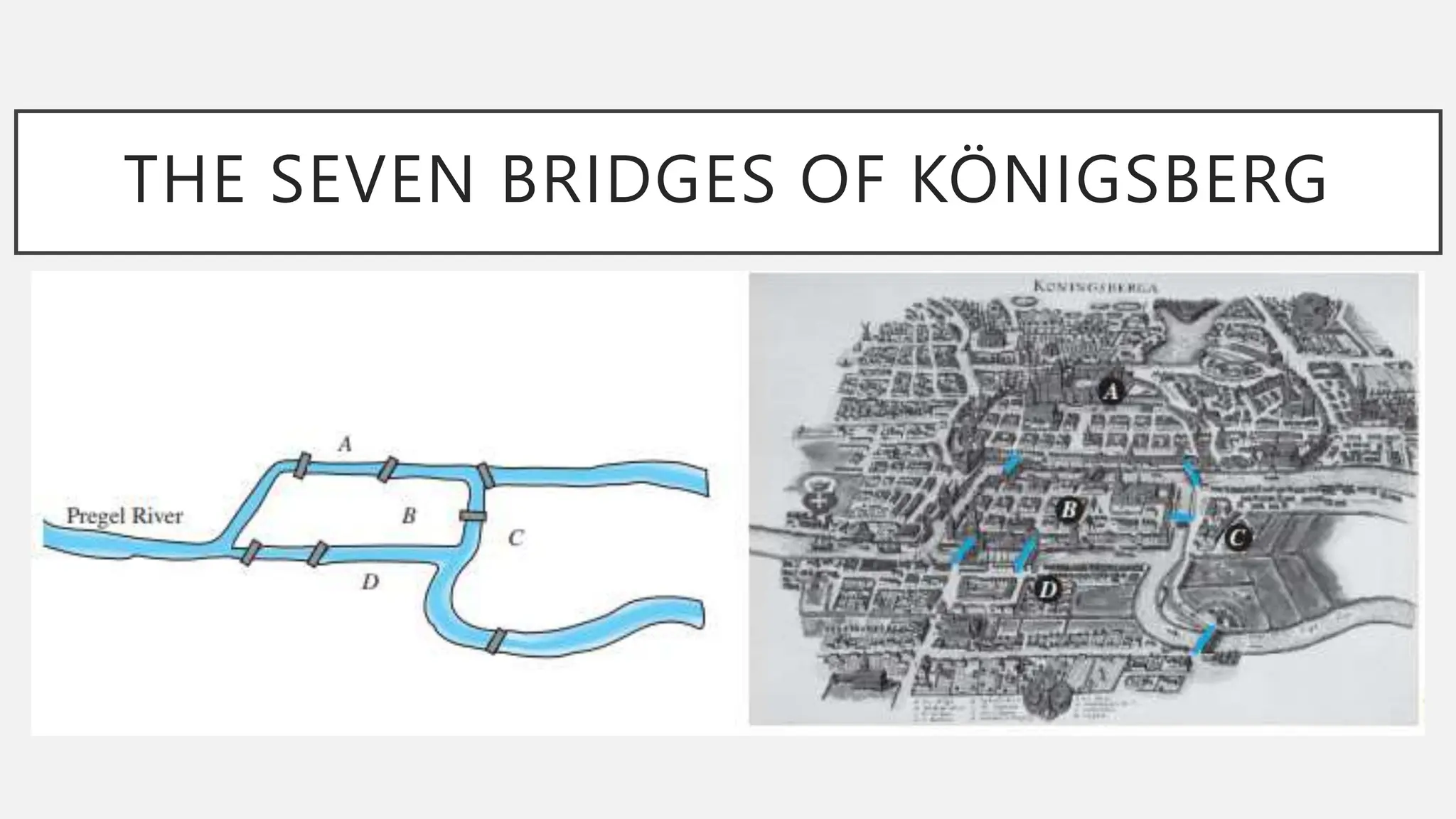
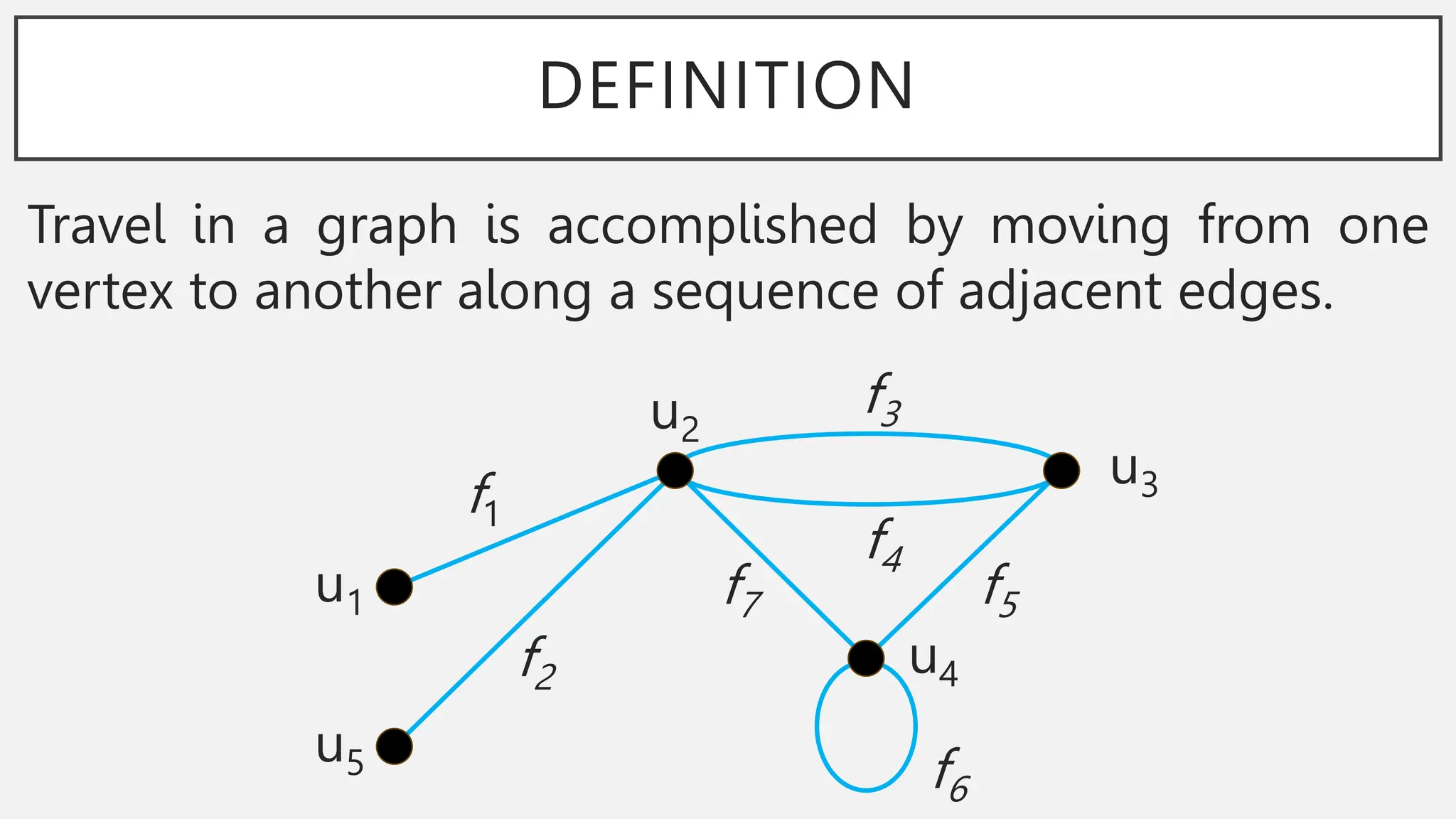
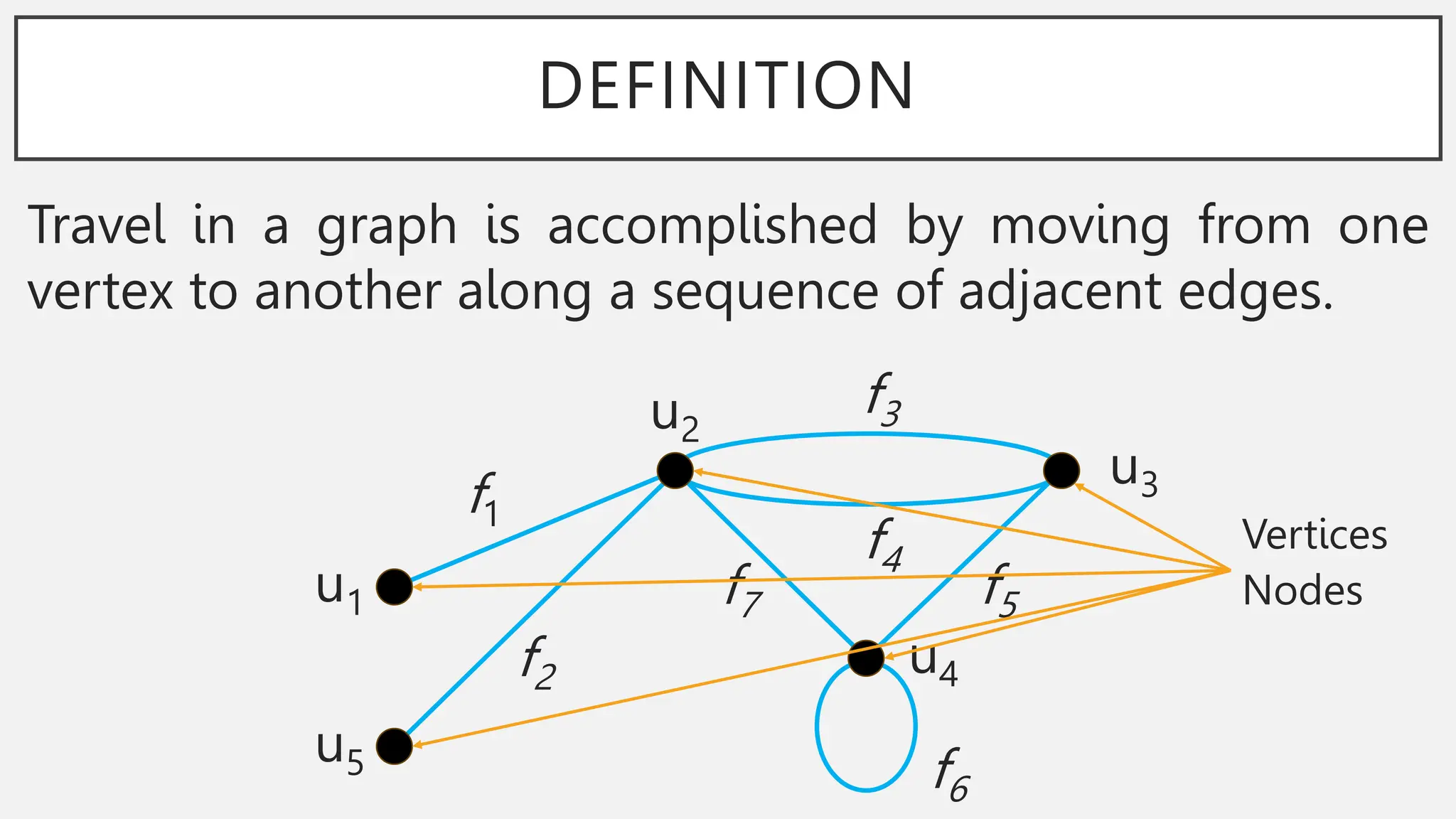
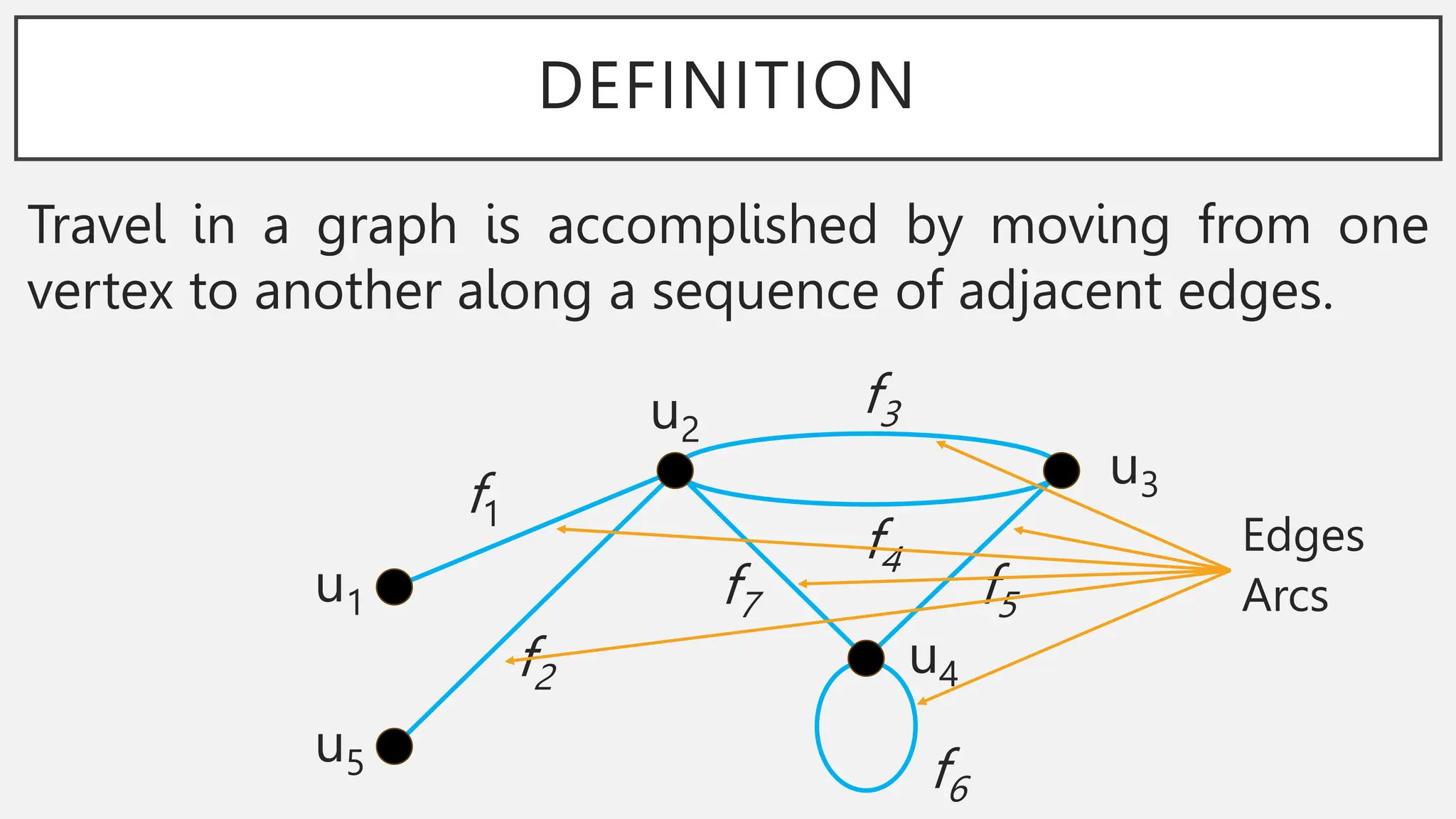
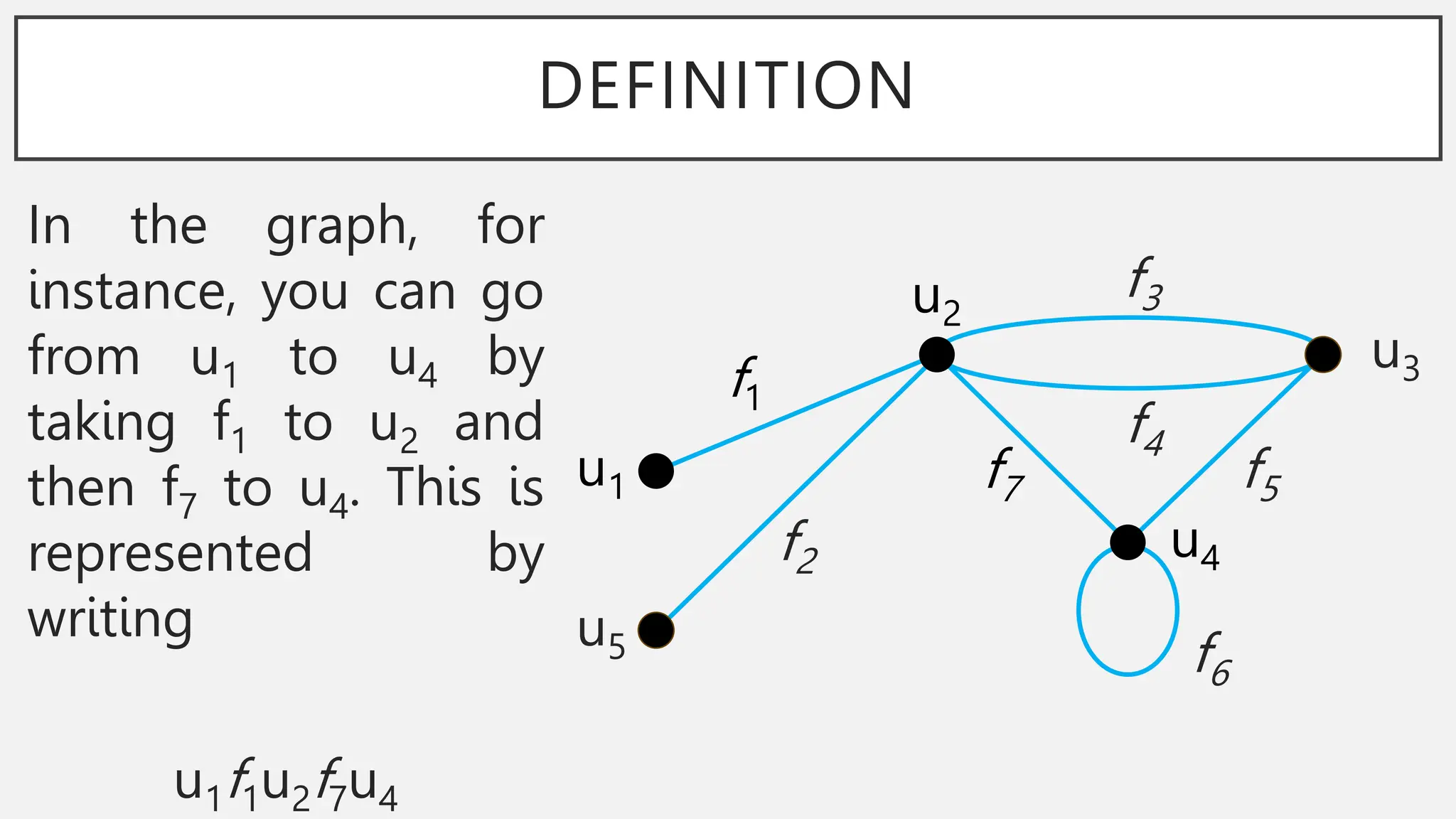
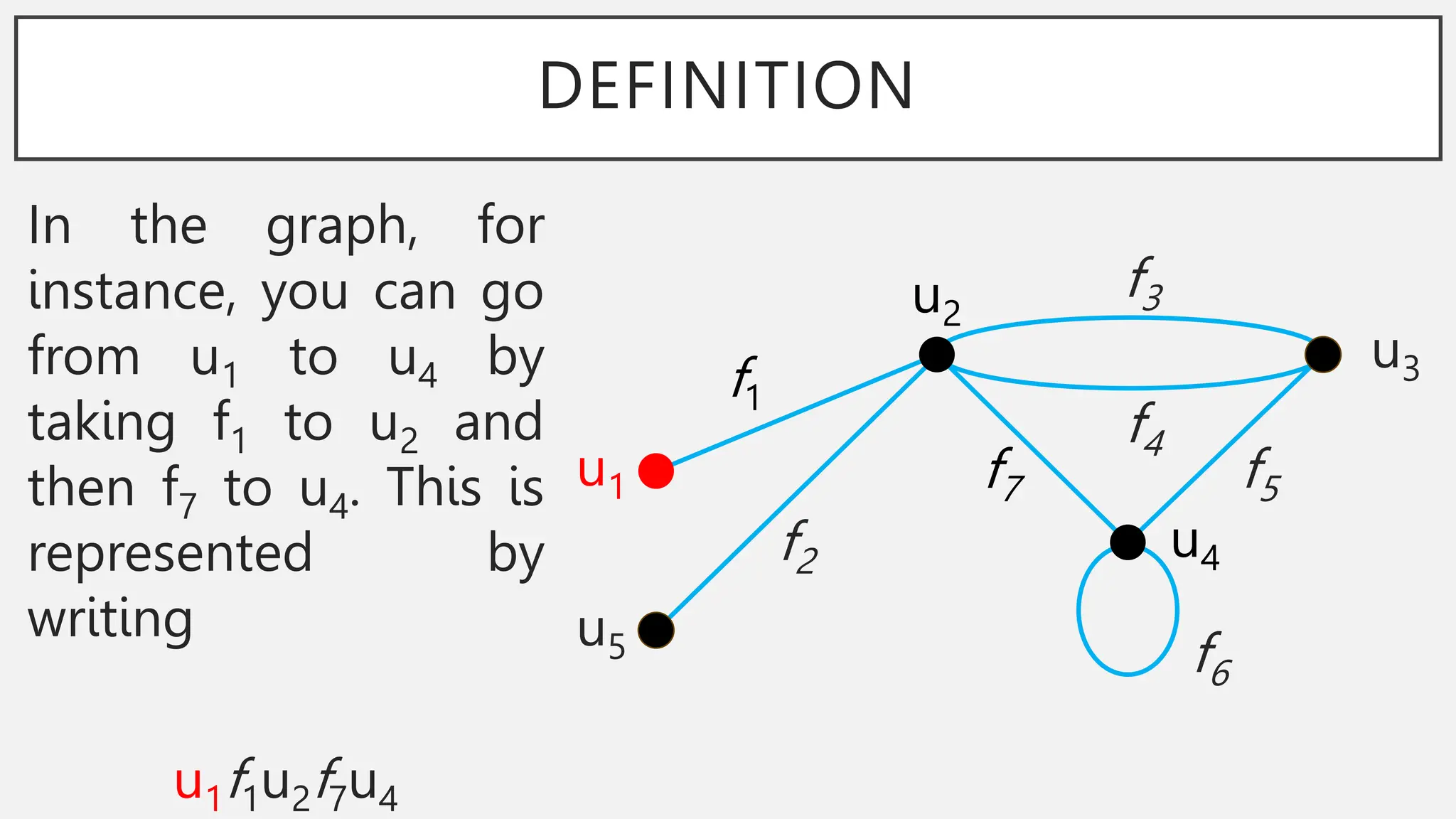
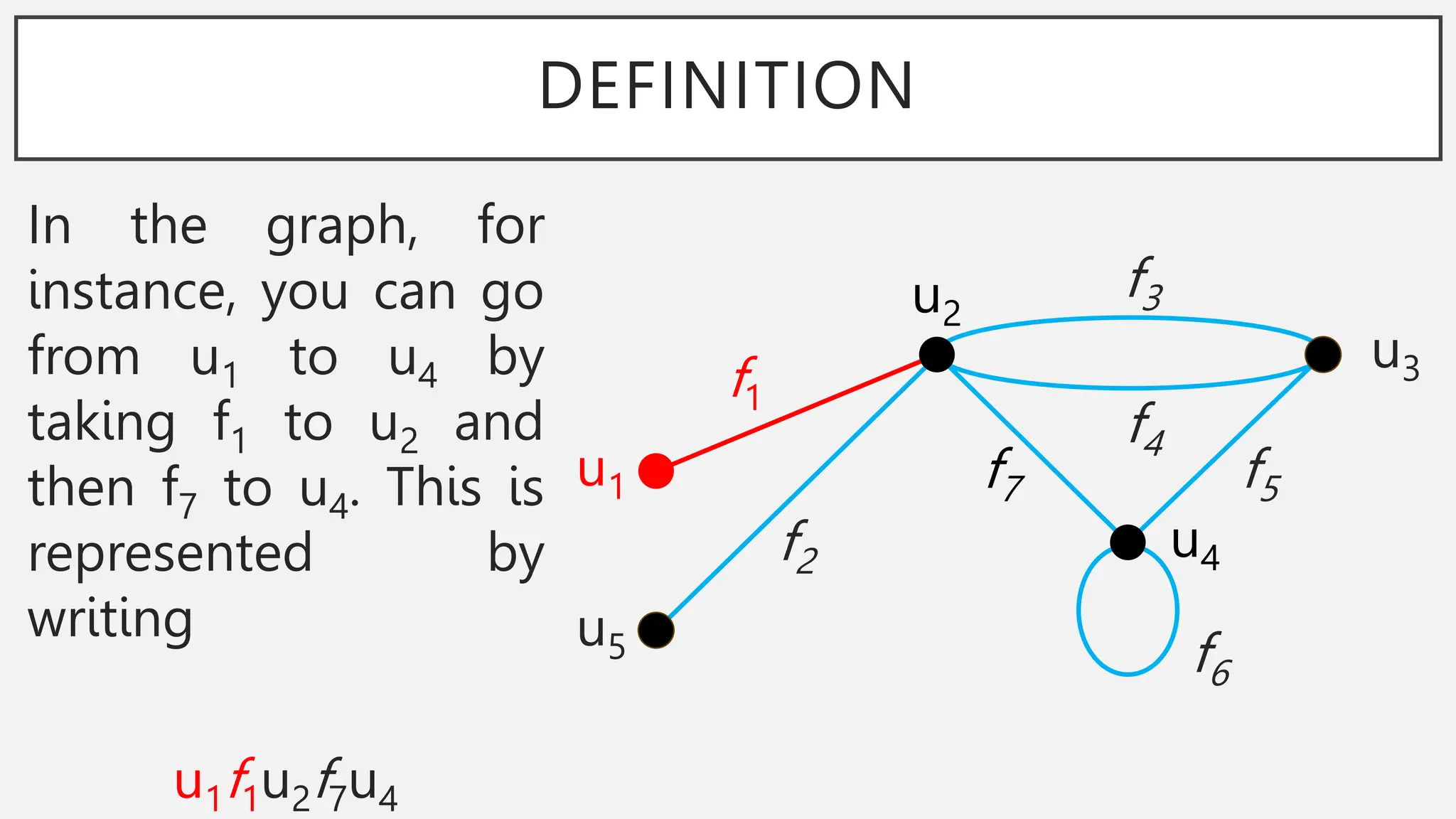
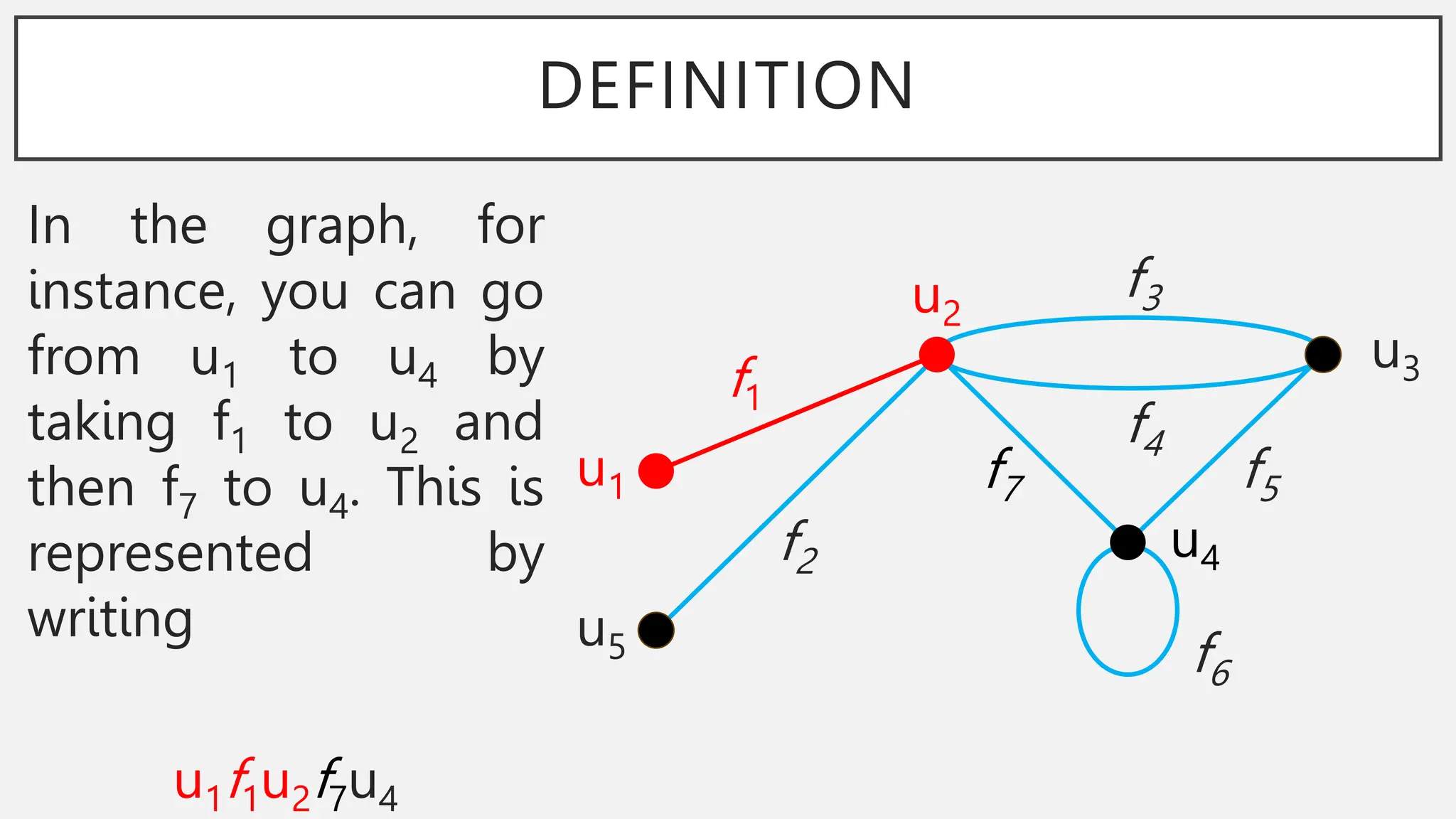
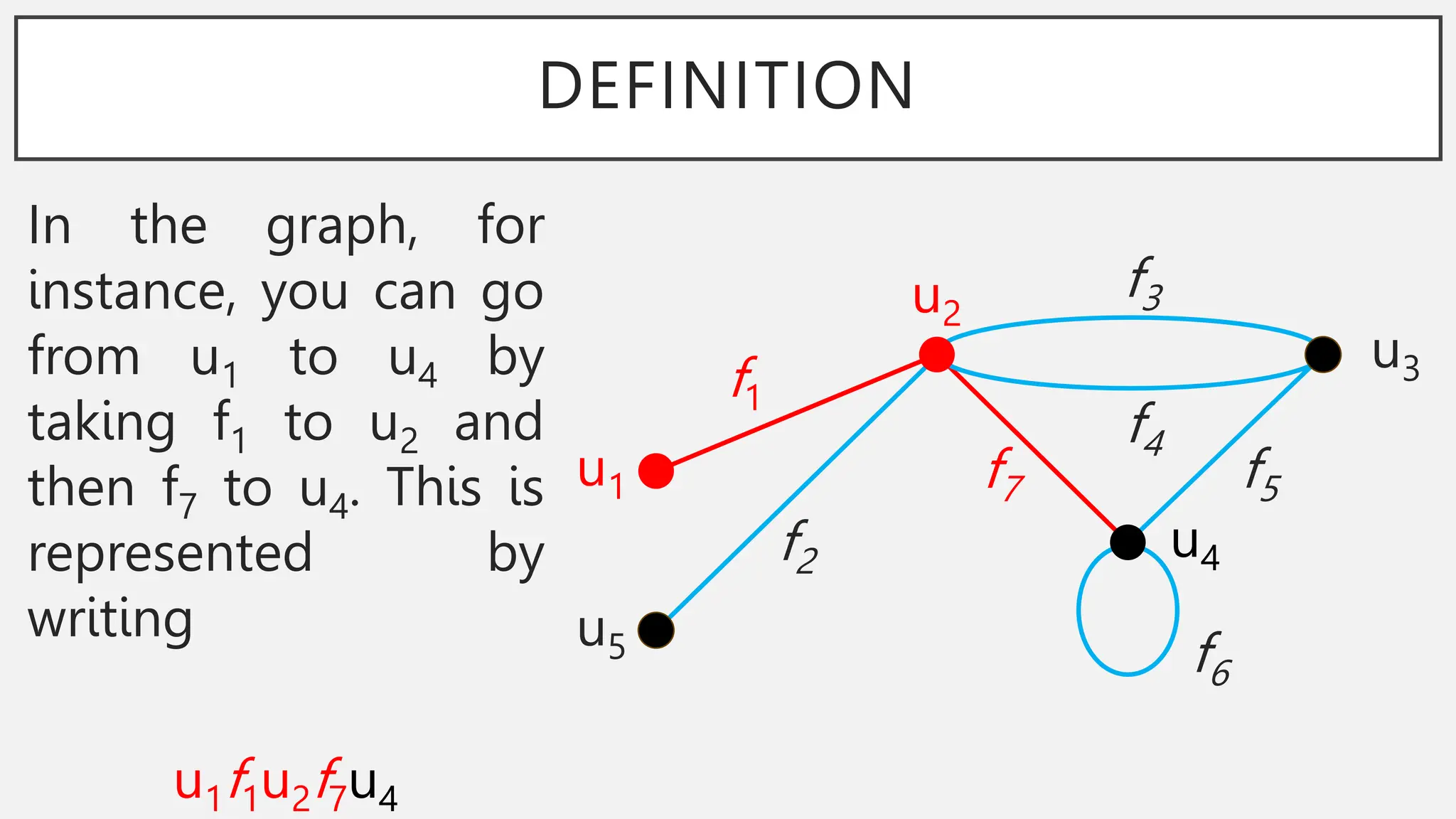
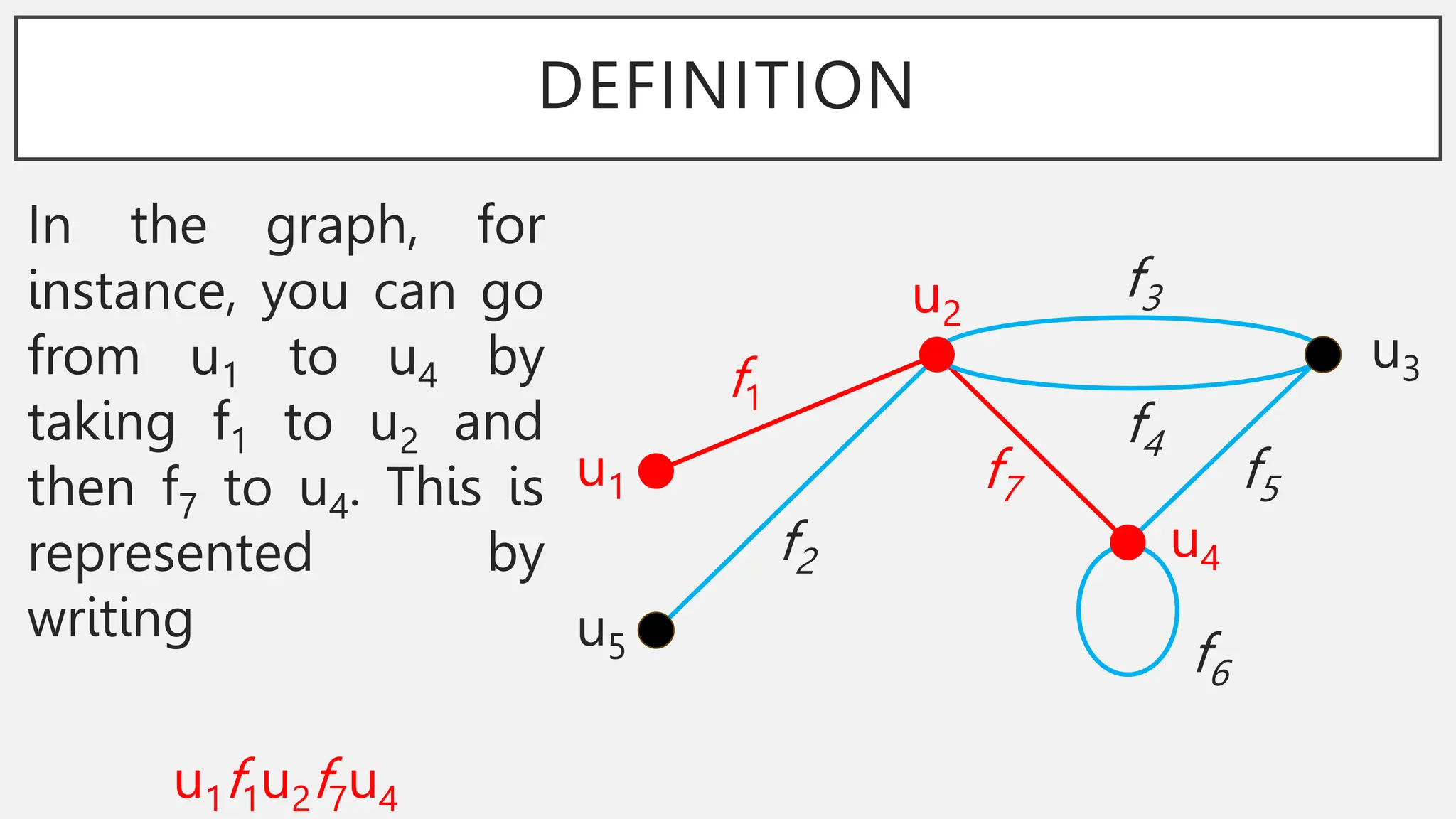
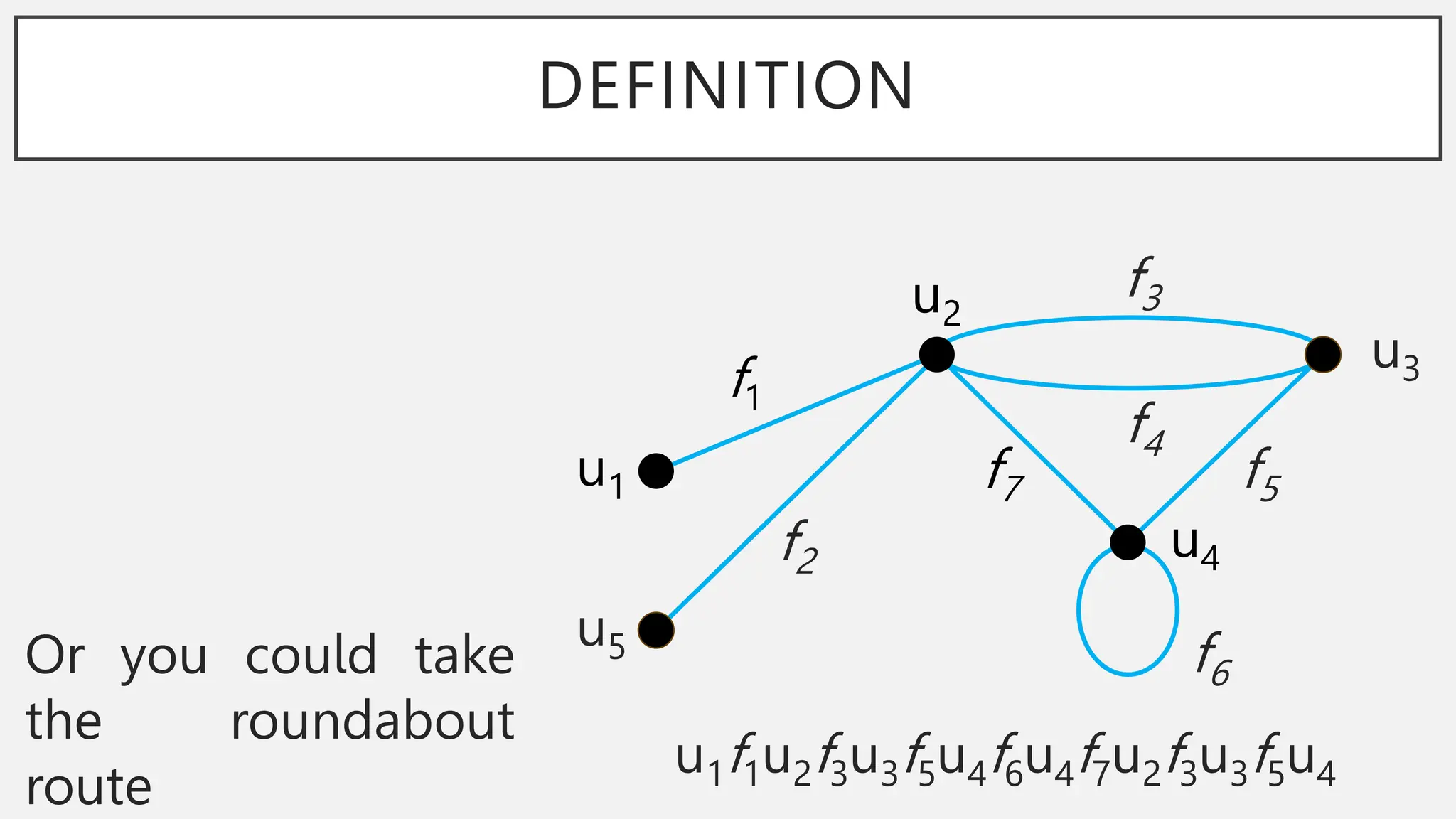
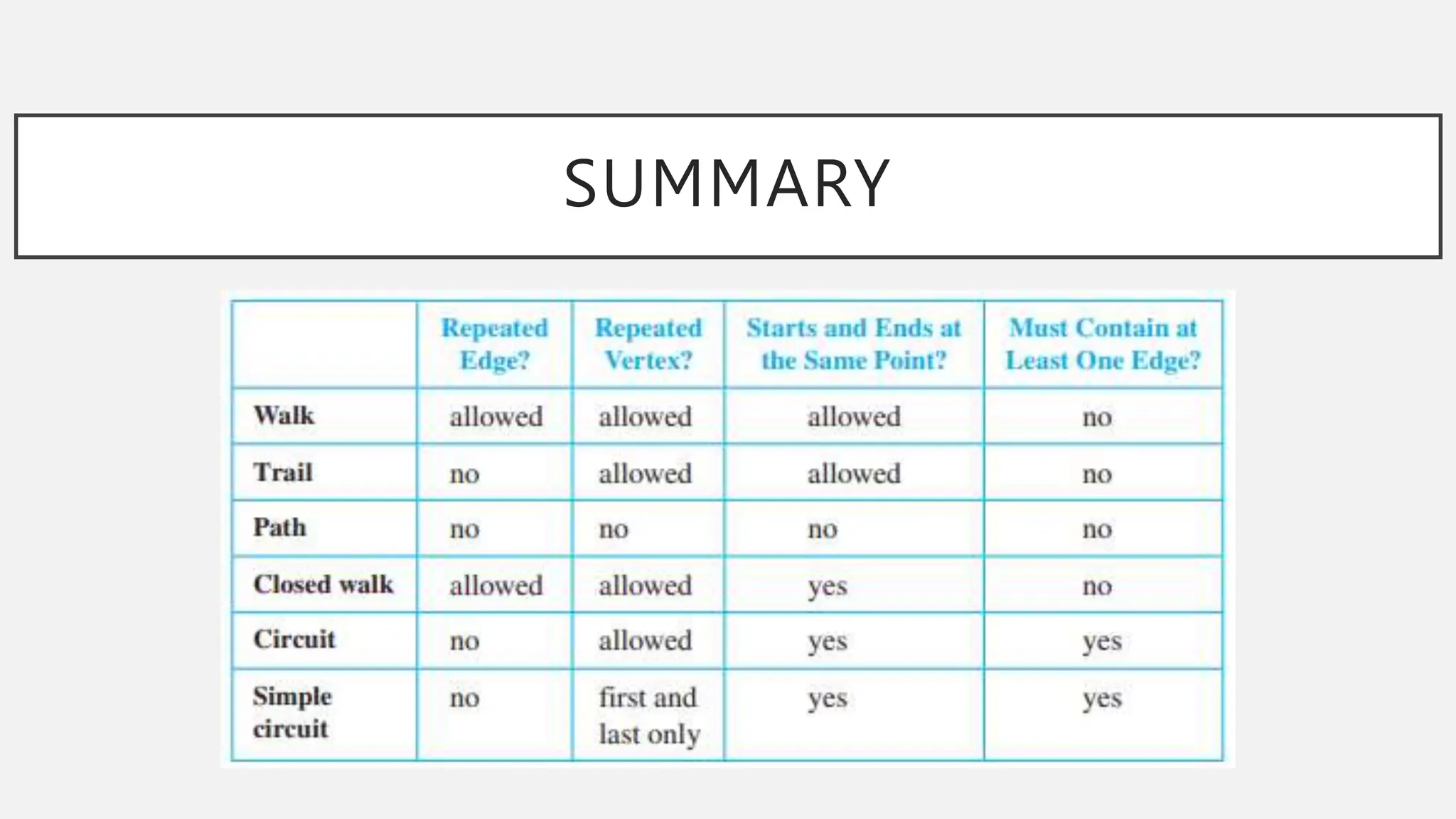
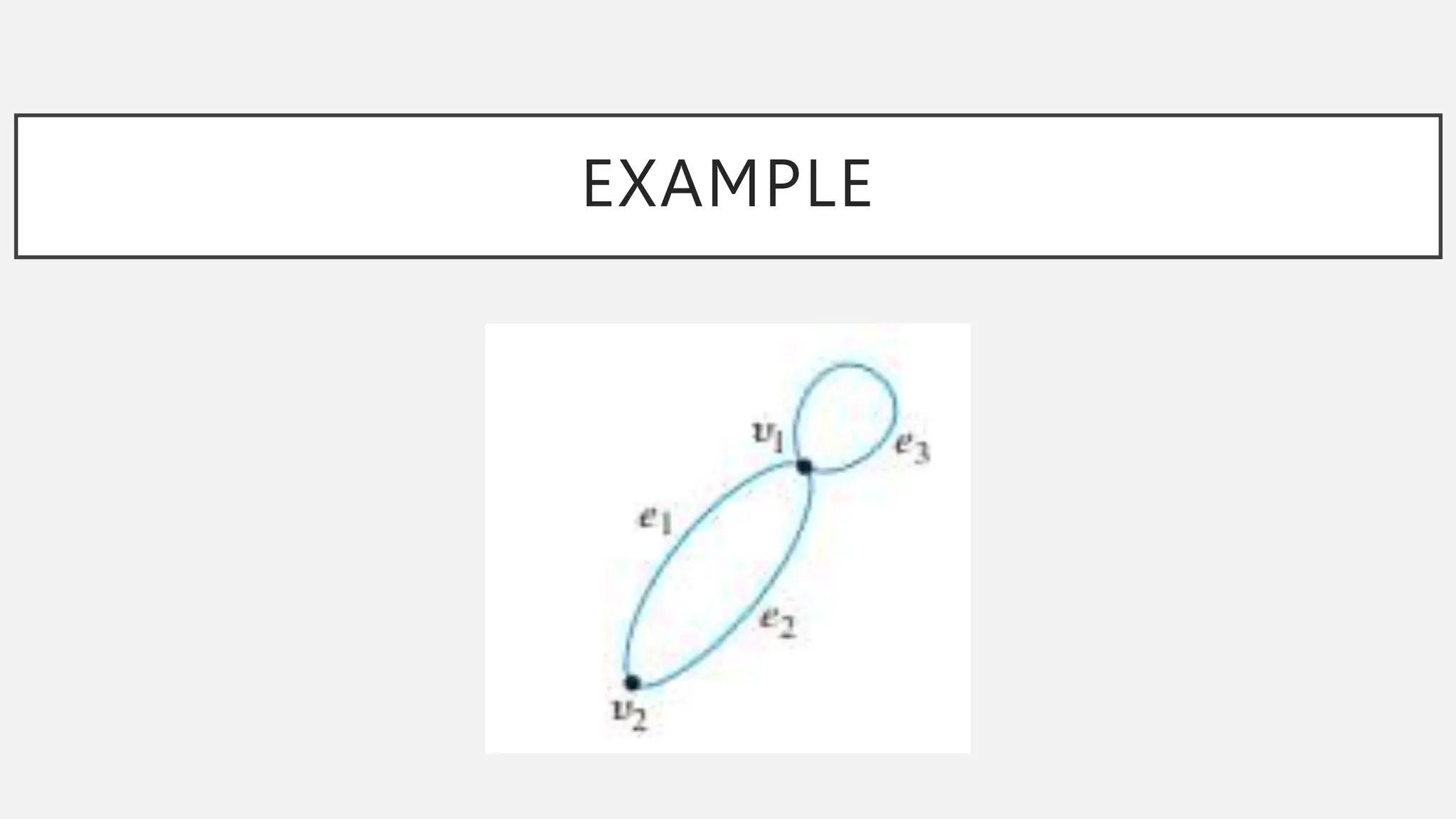
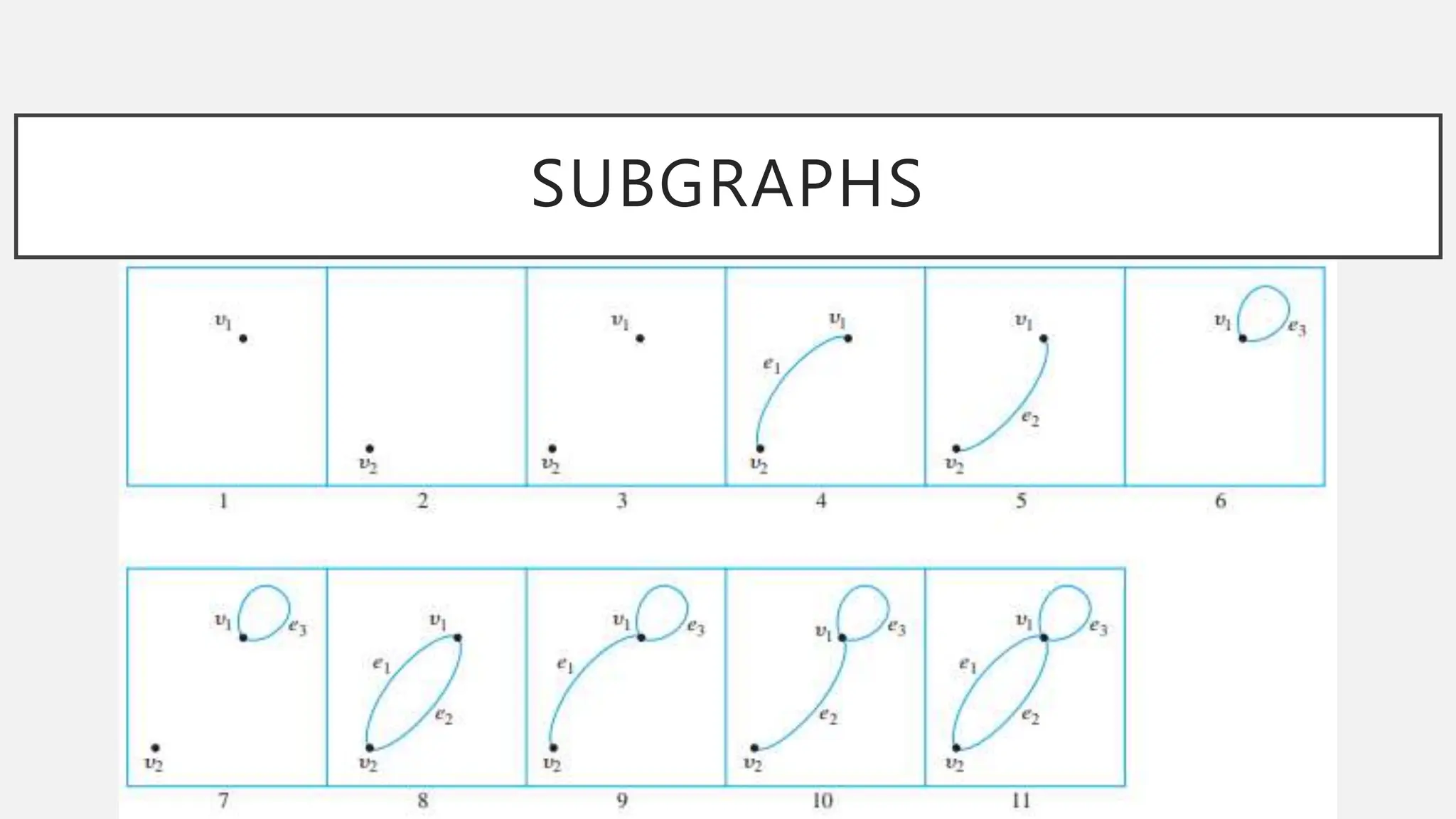
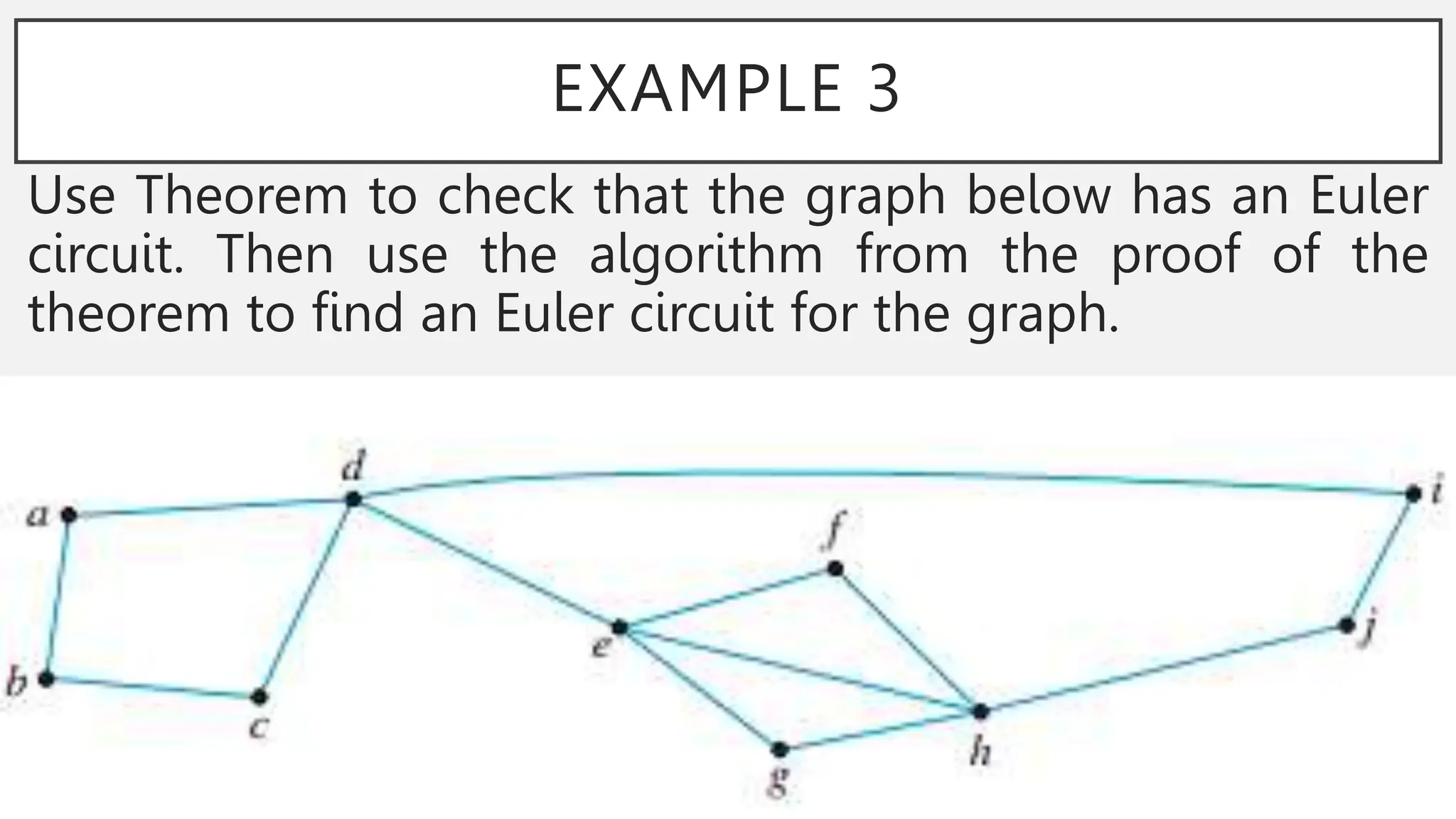
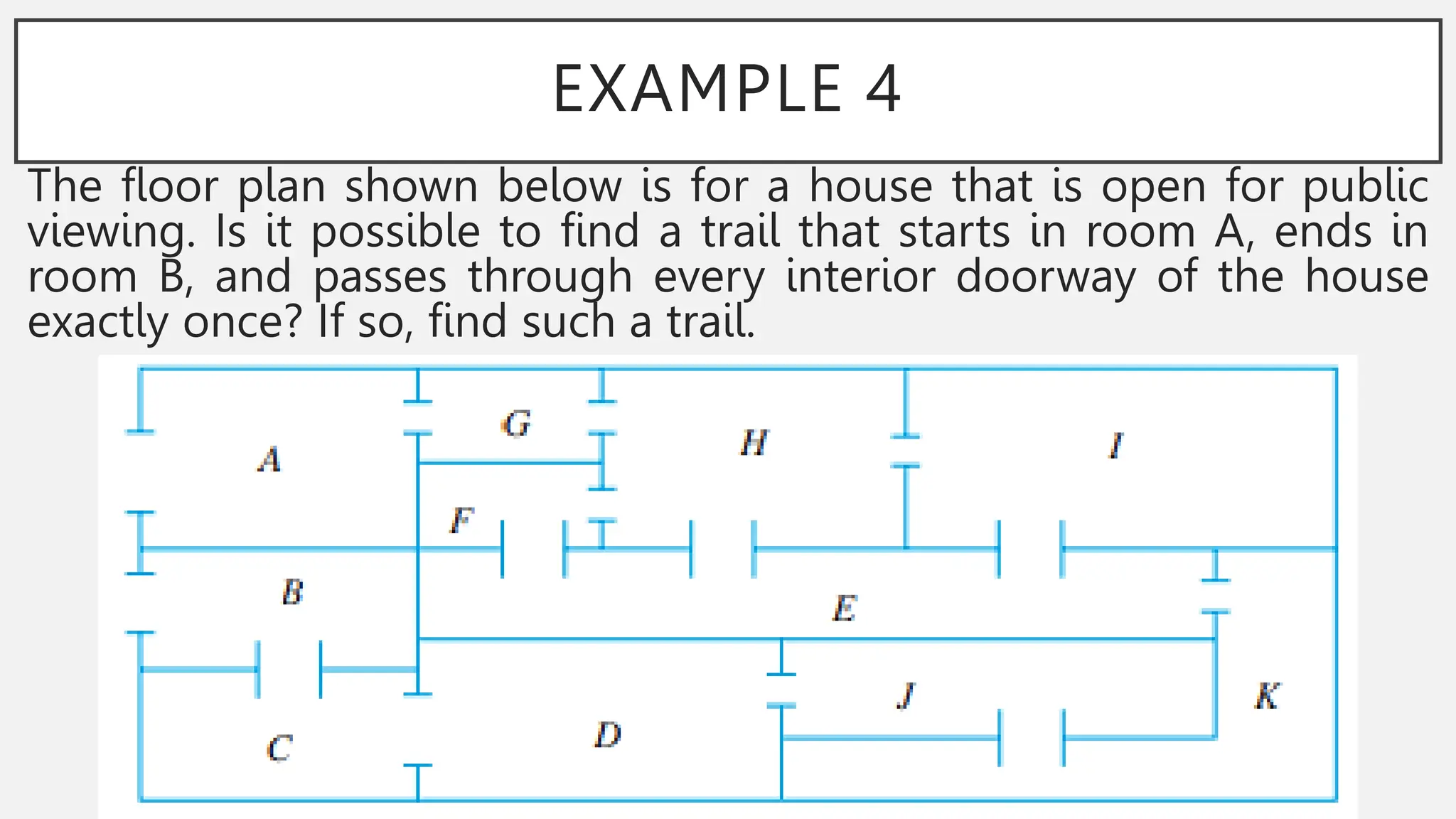
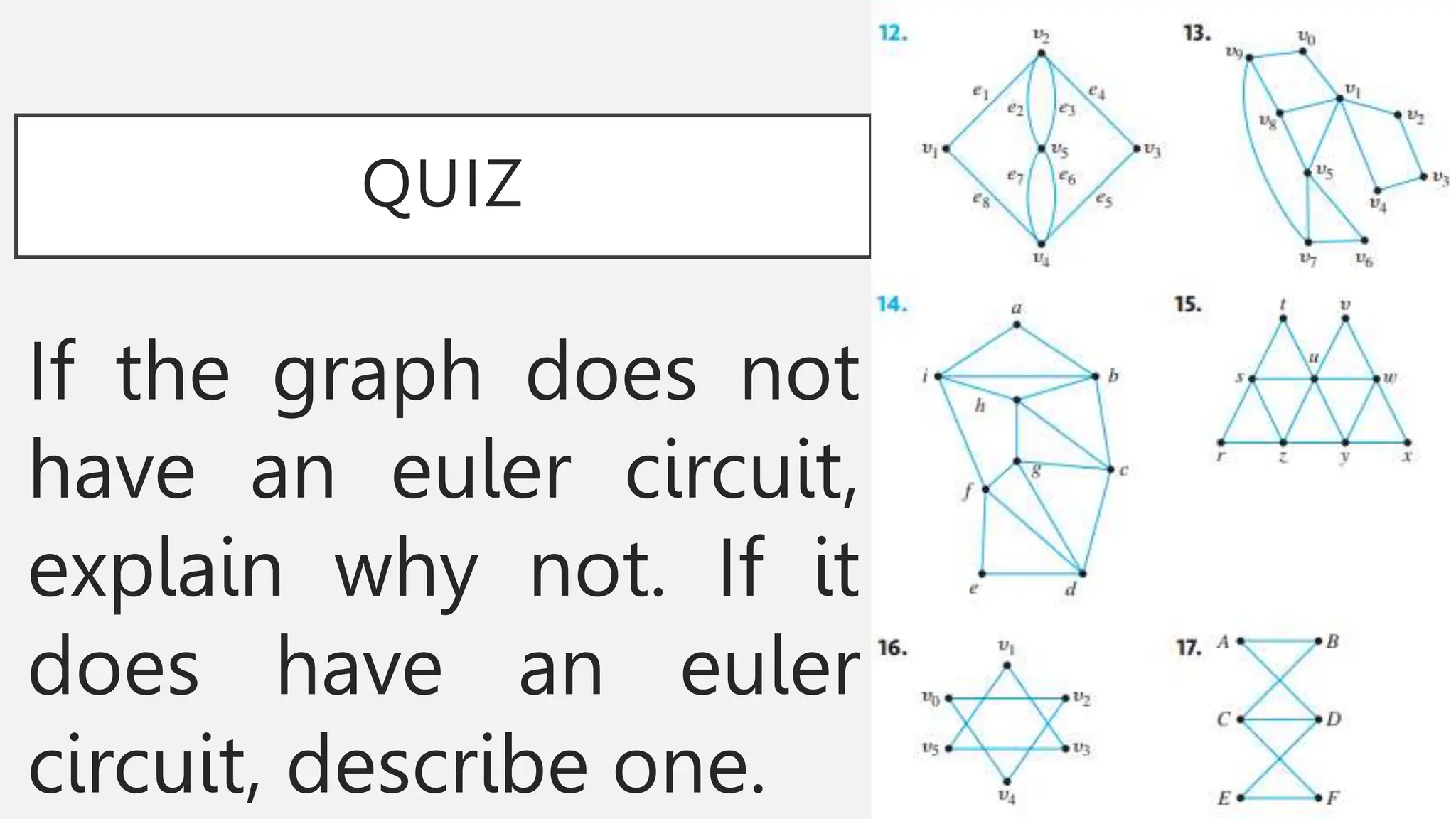
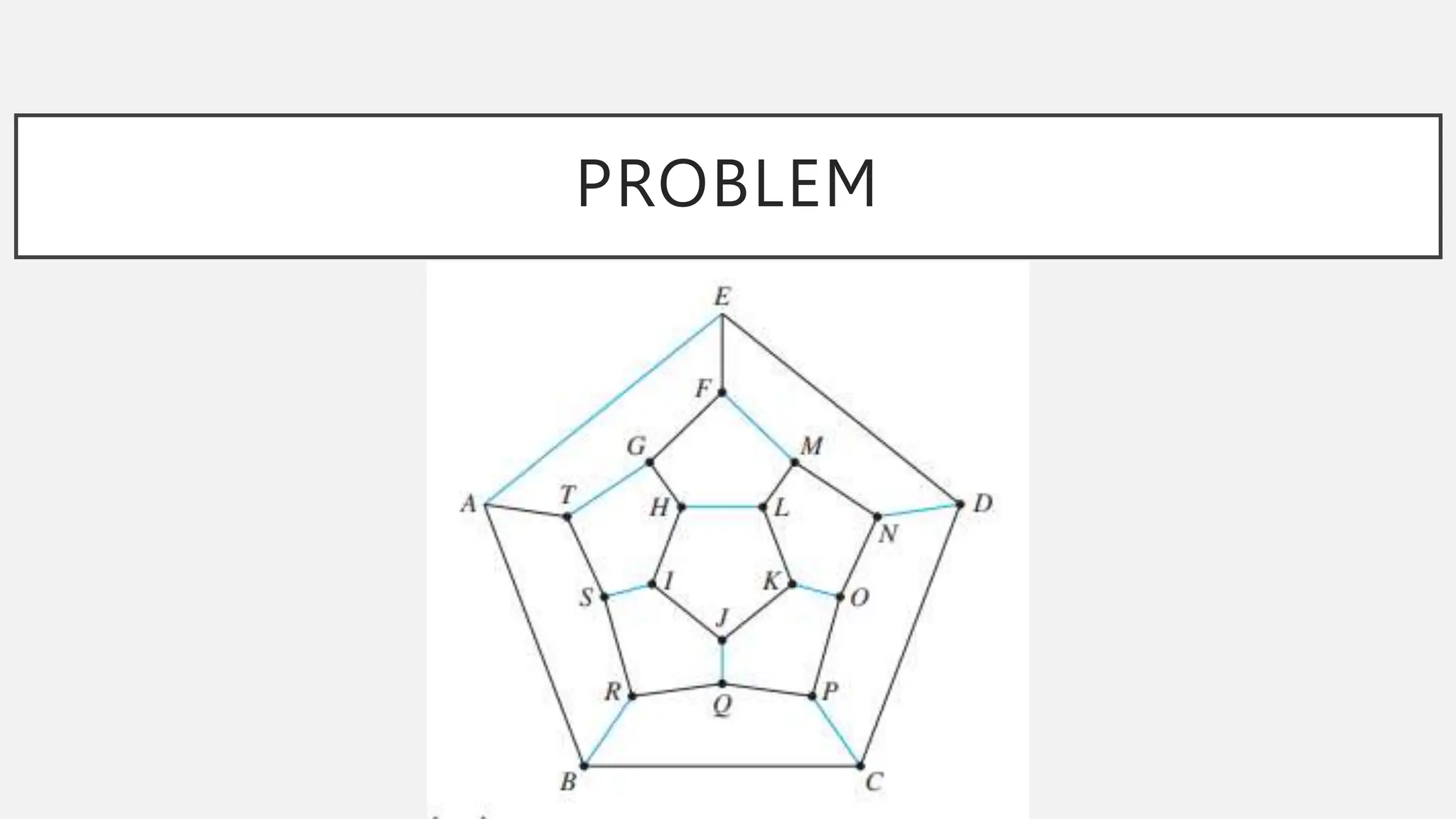
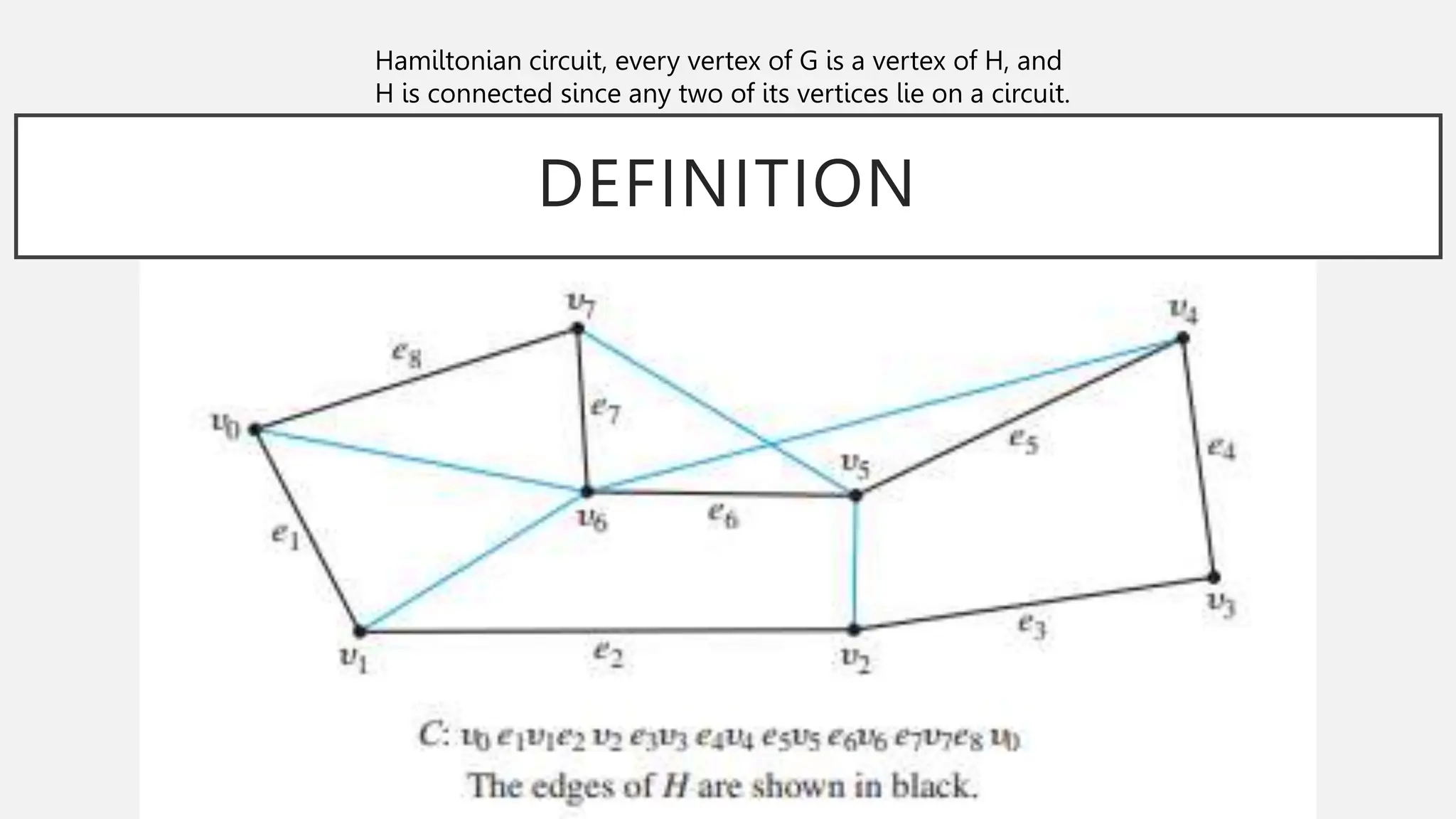
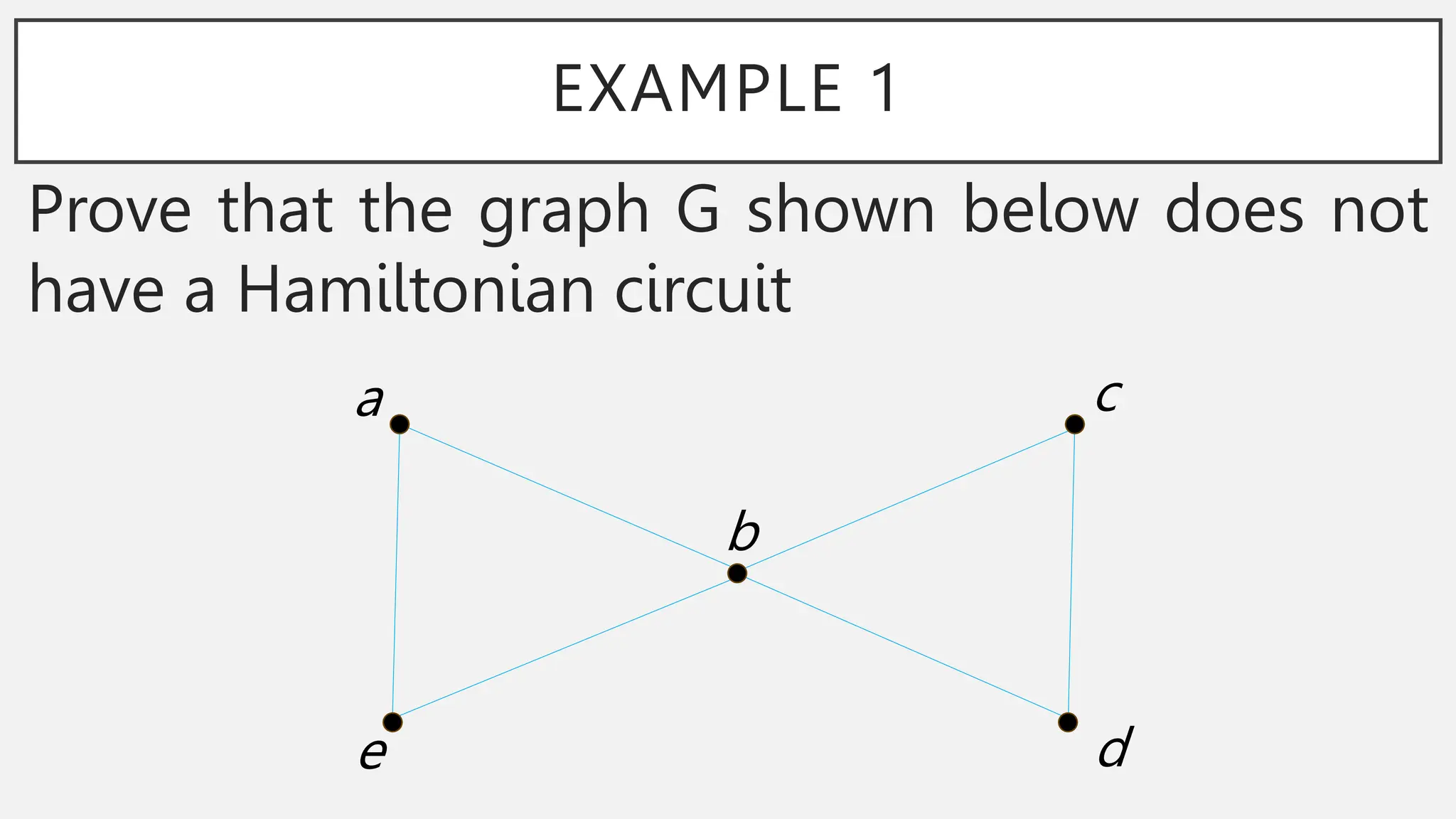
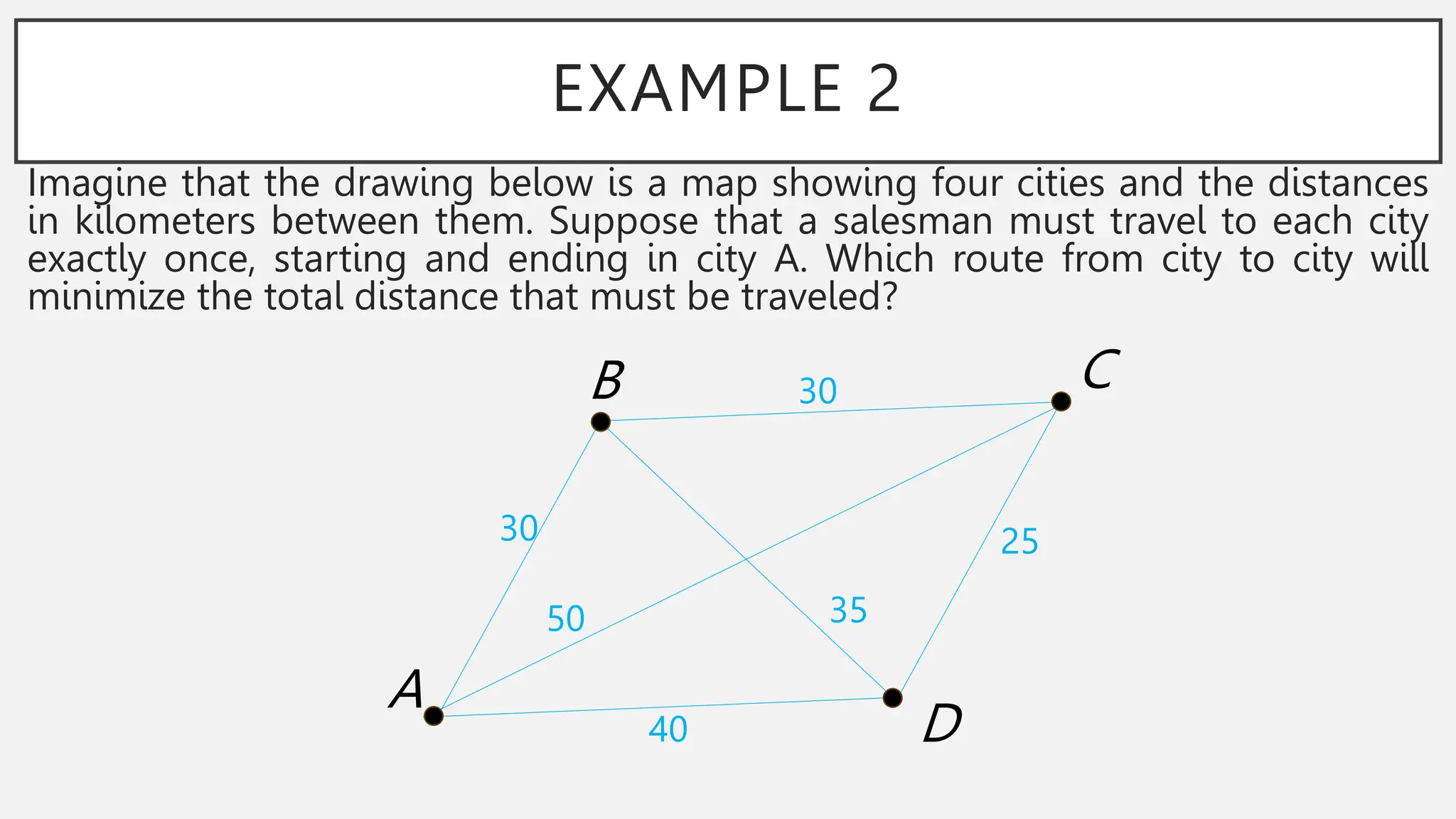
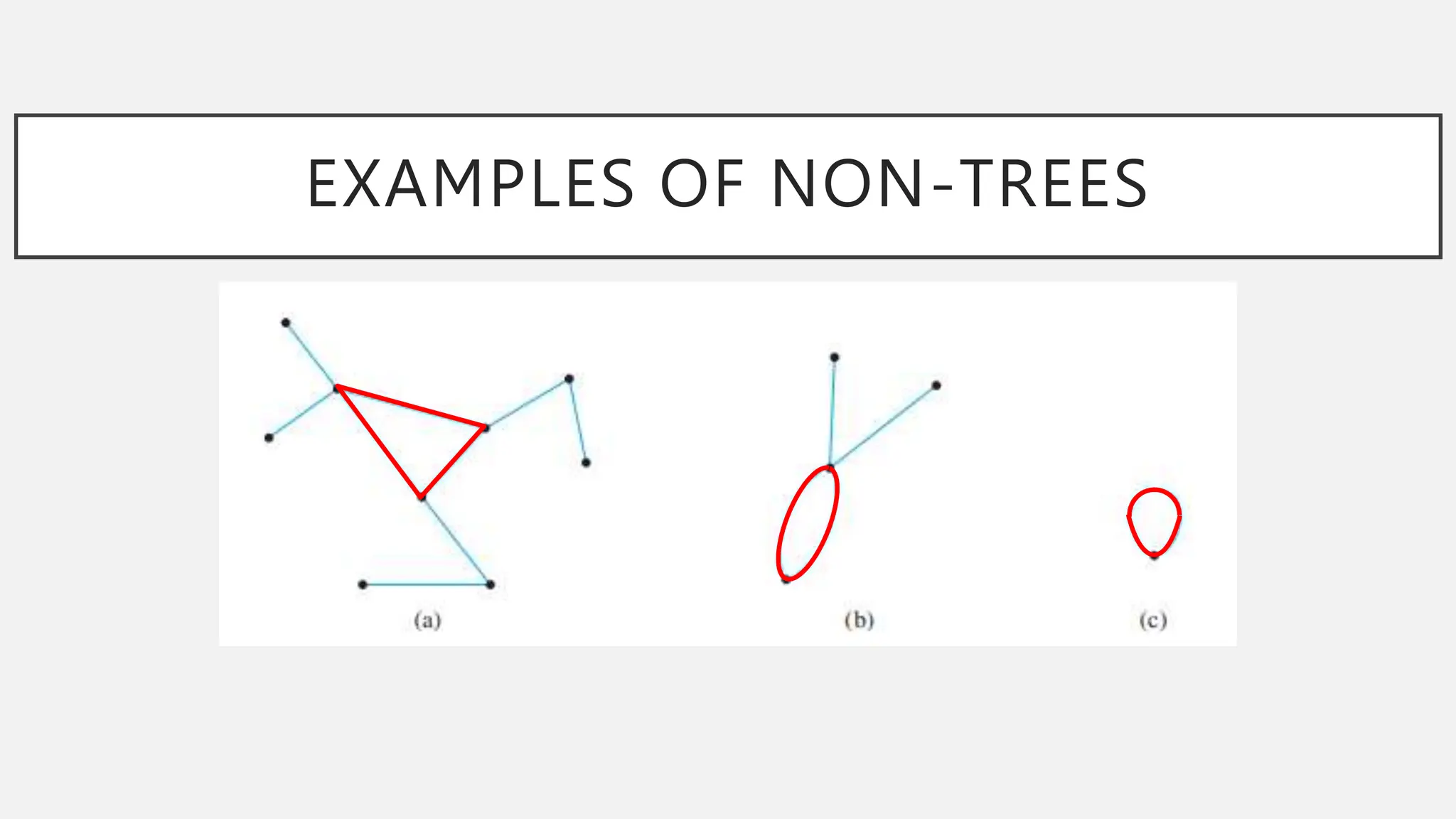
The document discusses graphs and circuits on graphs. It defines key graph terminology like vertices, edges, walks, paths, circuits, connectedness, subgraphs, and Euler and Hamiltonian circuits. It presents theorems characterizing when a graph has an Euler circuit or Euler trail. For example, a graph has an Euler circuit if and only if it is connected and every vertex has even degree. It also provides examples and algorithms for determining if graphs have certain circuits.























![PROOF (ALGORITHM)
Suppose that G is any connected graph and suppose that every
vertex of G is a positive even integer. [We must find an Euler
circuit for G.] Construct a circuit C by the following algorithm:
Step 1:
Pick any vertex v of G at which to start.
[This step can be accomplished because the vertex set of G is
nonempty by assumption.]](https://image.slidesharecdn.com/final-termcoverage-240226025049-fbeb8e8e/75/Final-term-Coverage-pptx-42-2048.jpg)





























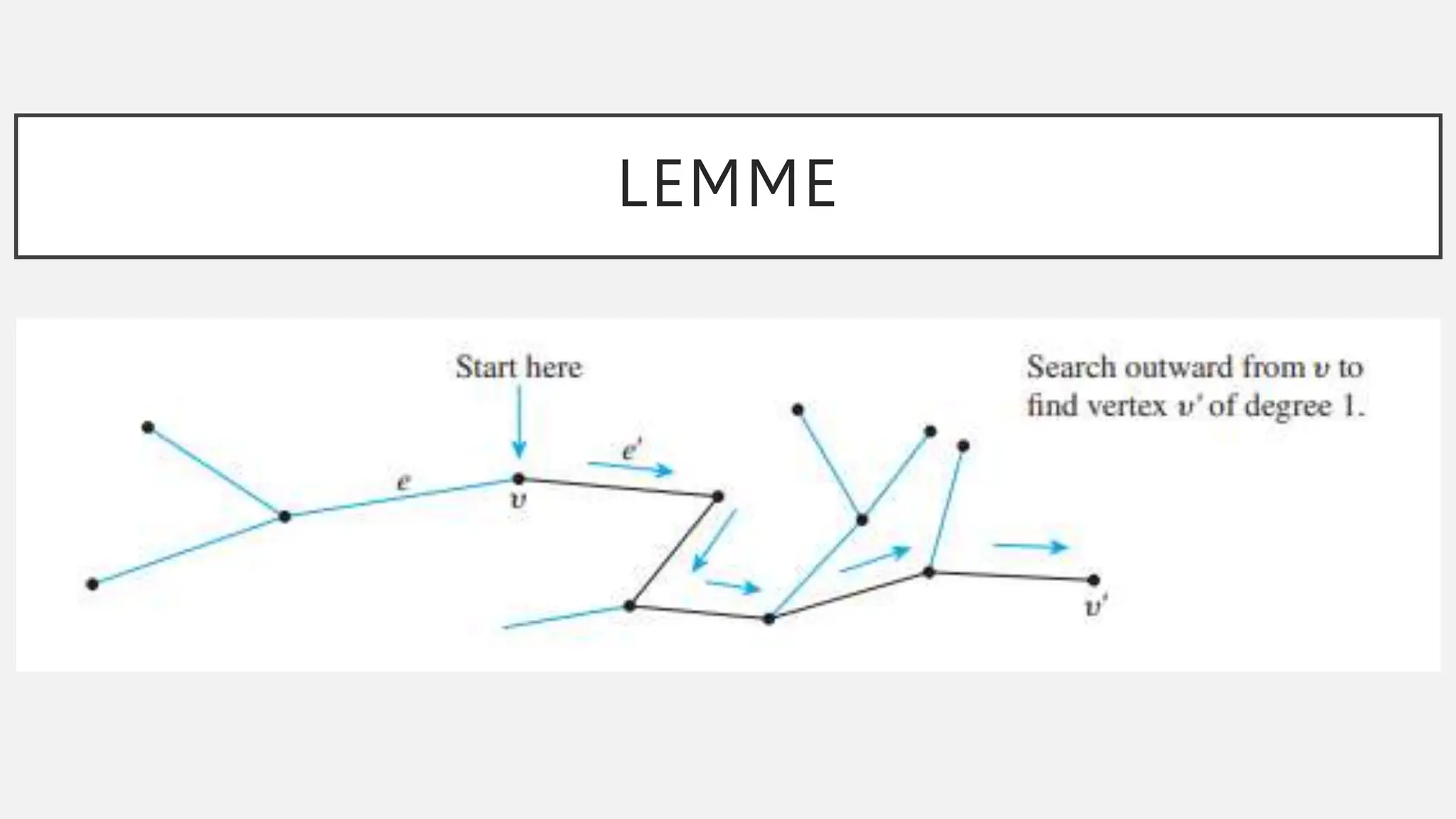


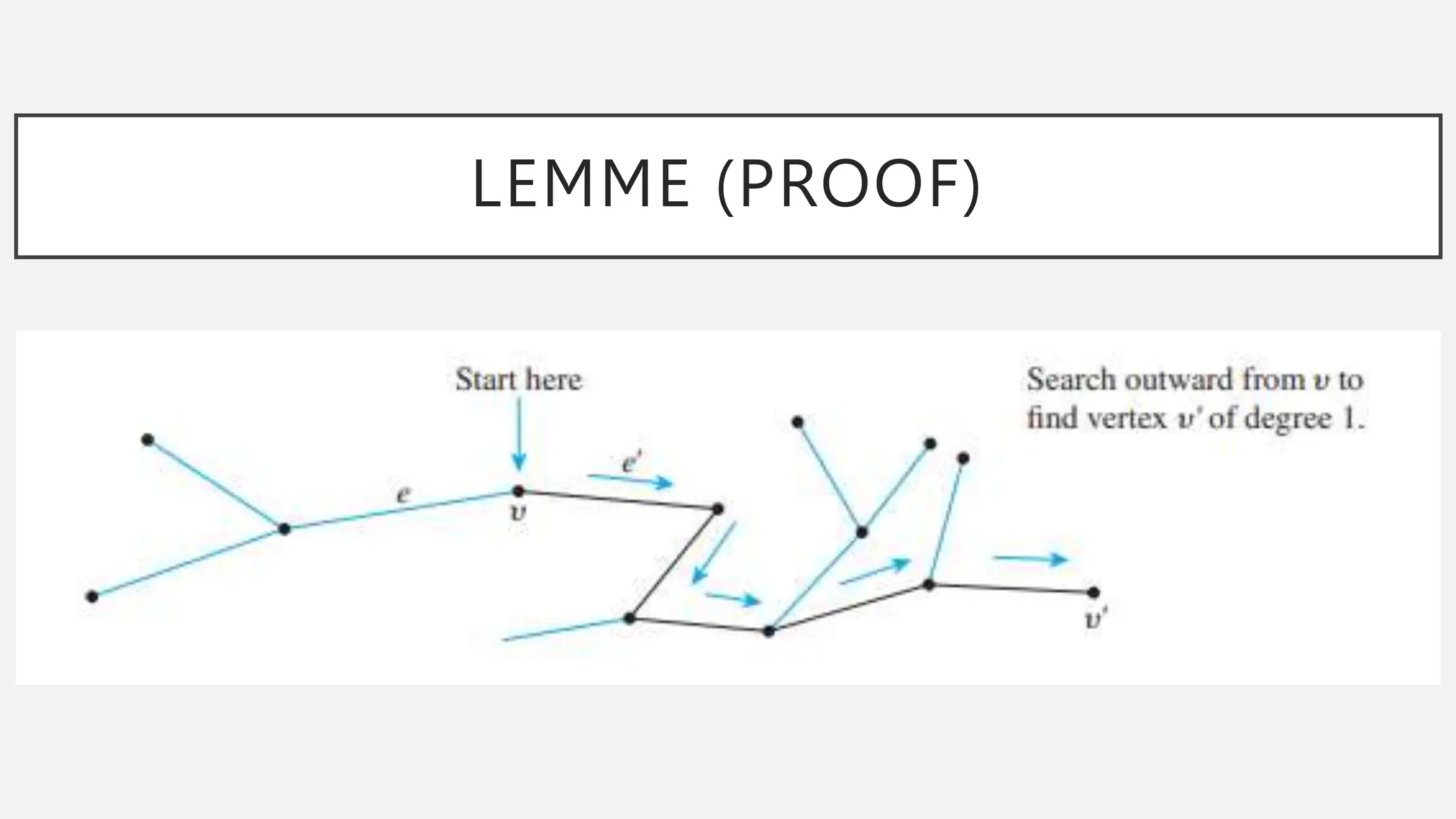
![LEMME (PROOF)
Step 2b: Let v’ be the vertex at the other end of e’
from v.
[Since T is a tree, e’ cannot be a loop and
therefore e’ has two distinct endpoints.]](https://image.slidesharecdn.com/final-termcoverage-240226025049-fbeb8e8e/75/Final-term-Coverage-pptx-85-2048.jpg)
![LEMME (PROOF)
Step 2c: Let e = e’ and v = v’.
[This is just a renaming process in
preparation for repeating step 2.]
The algorithm just described must eventually terminate
because the set of vertices of the tree T is finite and T is
circuit-free. When it does, a vertex v of degree 1 will
have been found.](https://image.slidesharecdn.com/final-termcoverage-240226025049-fbeb8e8e/75/Final-term-Coverage-pptx-86-2048.jpg)