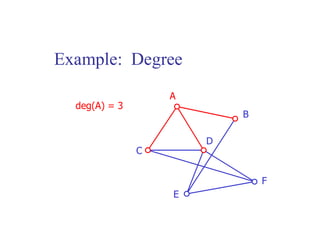
The document discusses different types of graphs and paths in graph theory: - It defines a graph as a set of vertices connected by edges, and defines directed and simple graphs. It provides an example of each. - It discusses terminology related to graphs like adjacent vertices, endpoints of edges, and subgraphs. - It defines the degree of a vertex and total degree of a graph. It provides an example calculation of vertex degree. 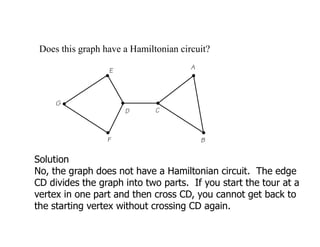- It defines different types of paths in graphs like simple paths, circuits, and simple circuits. It provides examples of each. 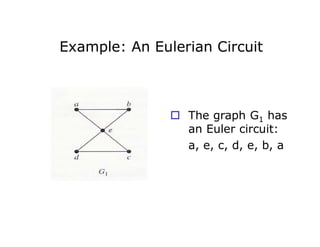- It defines Eulerian circuits and paths as paths or circuits that pass through each edge exactly once. It provides examples of graphs that do

1. Graph theory
a graph is a finite set of dots called vertices (or nodes) connected by
links called edges (or arcs).
a simple graph is set of vertices V and set of unordered pairs of distinct
elements of V called edges.

2. Example: Graph
• Let G = (V, E) where
– V = {A, B, C, D, E},
– E = {{A, B}, {A, C}, {A, C}, {B, B}, {B, C},
{D, E}}.
D
A
B
C
E
D
A
B
C
E

3. kavita hatwa math 231 fall 2002
Terminology
• The edge {a, b} has endpoints a and b.
• The edge {a, b} connects the endpoints a
and b.
• Vertices that are connected by an edge are
adjacent.

4. Directed Graphs
• A directed graph G is a pair (V, E) where
– V is a set of vertices,
– E is a multiset of ordered pairs of vertices.
• That is, each edge has a direction.
• A directed graph is also called a digraph.

5. Example: Directed Graph
 Let G = (V, E) where
 V = {A, B, C, D, E},
 E = {(A, B), (A, C), (C, A), (B, B), (B, C),
(D, E)).
A
B
C D
E

6. Simple Graphs
• A simple graph G is a pair (V, E) where
– V is a set of vertices,
– E is a set of edges,
where each edge is a set of vertices.

7. Subgraphs
• A graph H = (V(H), E(H)) is a subgraph of a
graph G = (V(G), E(G)) if V(H)  V(G) and
E(H)  E(G).

8. A
B
C
D
E
F
G = {A, B, C, D, E, F}
H = {A, C, D, F}

9. Degree of a Vertex
• The degree of a vertex v is the number of
edges that include v.
• The total degree of a graph G is the sum of
the degrees of its vertices.

10. Example: Degree
A
B
C
D
E
F
A
deg(A) = 3

11. • A path from v to w is a walk from v to w in which
the edges are distinct.
• A simple path from v to w is a path from v to w in
which the vertices are distinct.
• A circuit is a closed path.
• A simple circuit is a circuit in which the vertices are
distinct, except for the first and last vertices.

12. kavita hatwal math 231 fall 2002
Example: A Path
• A path from A to F.
A
B
C
D
E
F

13. Example: A Simple Path
• A simple path from A to F.
A
B
C
D
E
F

14. Example: A Circuit
• A circuit from A to A.
A
B
C
D
E
F

15. Example: A Simple Circuit
• A simple circuit from A to A.
A
B
C
D
E
F

16. An Eulerian or Euler Circuit
 An Euler circuit in a graph G is a simple circuit
containing every edge of G.
 An Euler path in G is a simple path containing every
edge of G.

17. An Eulerian or Euler Circuit
 An Euler path is a path that passes through each
edge of a graph exactly one time.
 An Euler circuit is a circuit that passes through each
edge of a graph exactly one time.

18.  The graph G1 has
an Euler circuit:
a, e, c, d, e, b, a
Example: An Eulerian Circuit

19.  The graph G2 and
G3 don’t have an
Euler circuit.
 G3 has an Euler
path:
a, c, d, e, b, d, a, b
 G2 does not have an
Euler path.
Example: An Eulerian Circuit

20. Example: An Eulerian Circuit
 H2 has an Euler
circuit:
a, g, c, b, g, e, d, f, a
 H1 nor H3 has an
Euler circuit.
 H3 has an Euler
path: c, a, b, c, d, b
 H1 does not have an
Euler path.
Example: An Eulerian Circuit

21.  G1 contains two
vertices of odd
degree (b and d).
 b and d must be
the end points of
this Euler path.
Example: Eulerian Path
 d, a, b, c, d, b is
an Euler path.

22.  G2 contains
exactly two
vertices of odd
degree (b and d).
 b and d must be
the end points of
this Euler path.
Example: Eulerian Path
 b, a, g, f, e, d, c,
g, b, c, f, d is an
Euler path.

23.  G3 has six
vertices of odd
degree.
 G3 has no Euler
path.
Example: Eulerian Path

24.  A Hamilton path in a graph G is a path which visits
every vertex in G exactly once.
 A Hamilton circuit is a Hamilton path that returns to
its start.
Hamiltonian path and circuit

25. Find a Hamiltonian circuit for this graph starting at A.
(Remember: unlike the Euler circuit, it is not
necessary to traverse every edge.)

26. Solution
These are the six possible Hamiltonian circuits starting from
A. If you got a different answer, did you add a vertex where
the diagonals cross? You shouldn’t have. Since a vertex has
not been indicated, edges AC and BD do not actually
intersect. (You may think of AC as representing a highway
overpass that is on a different level from edge BD.)
ABCDA, ACDBA, and ADBCA—as well as their reversals,
ADCBA, ABDCA, and ACBDA—are all Hamiltonian circuits.

27. Does this graph have a Hamiltonian circuit?
Solution
No, the graph does not have a Hamiltonian circuit. The edge
CD divides the graph into two parts. If you start the tour at a
vertex in one part and then cross CD, you cannot get back to
the starting vertex without crossing CD again.

28. Finding Hamilton Circuits
Which of these three figures has a Hamilton circuit?
Of, if no Hamilton circuit, a Hamilton path?