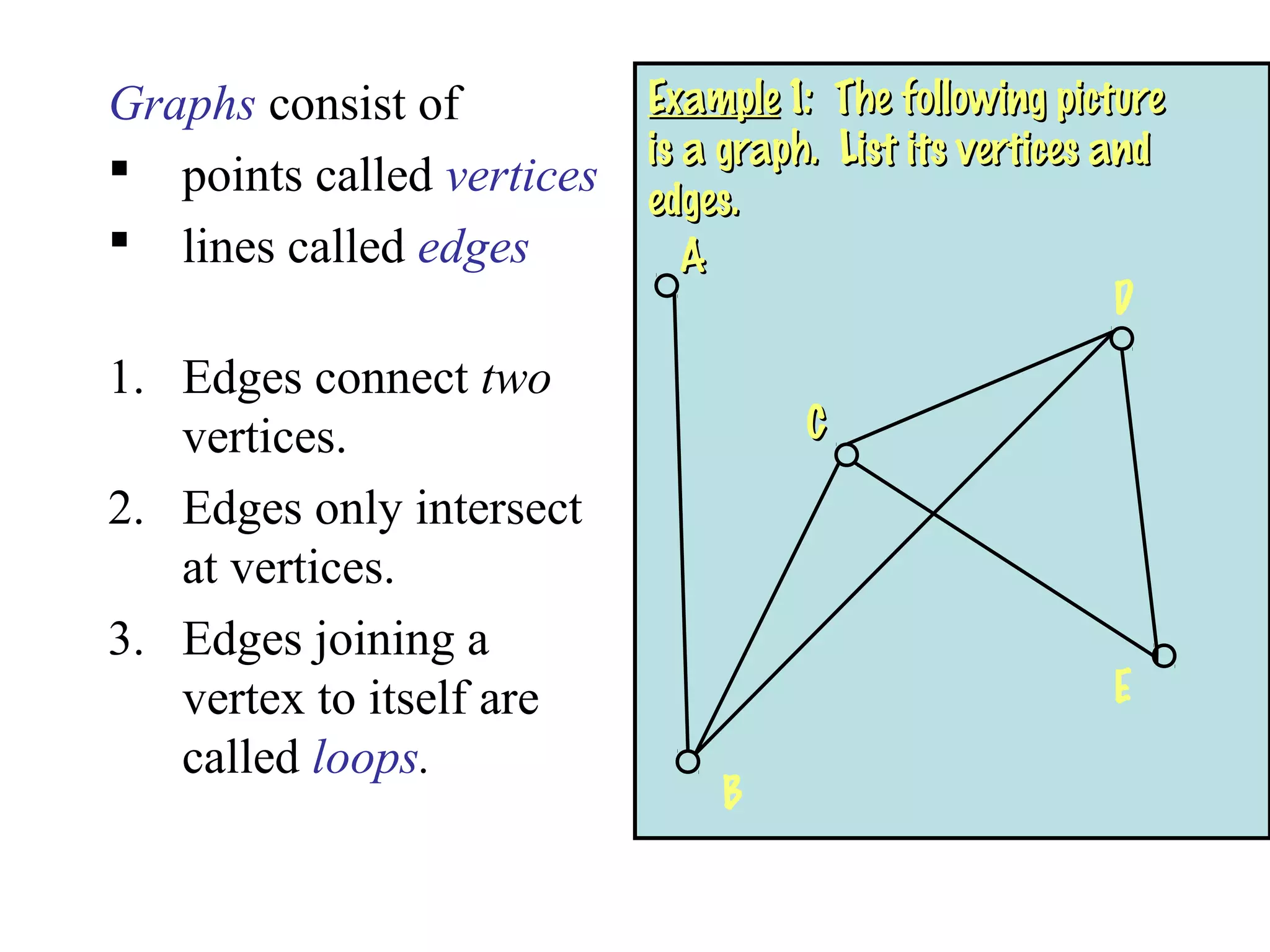
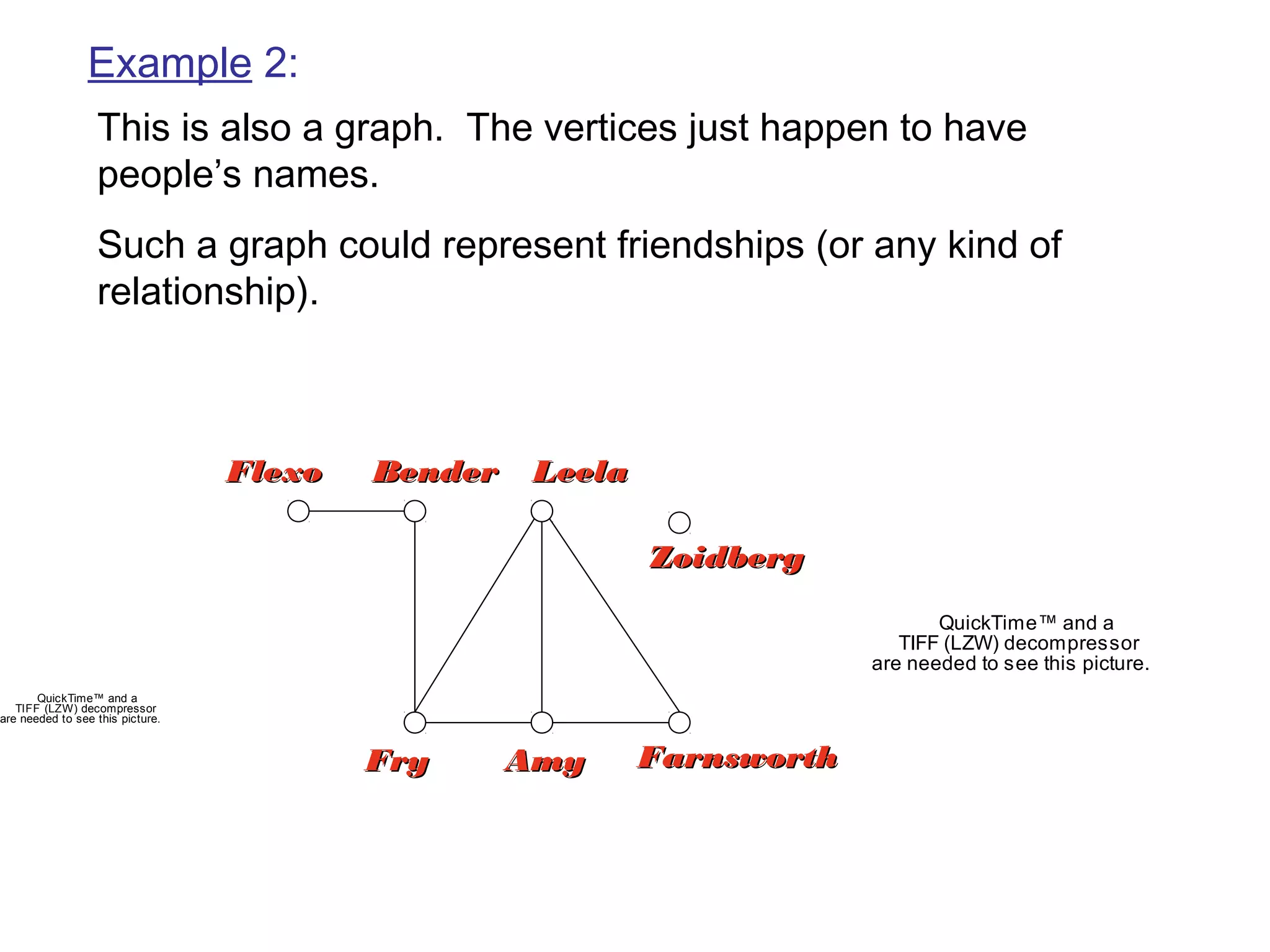
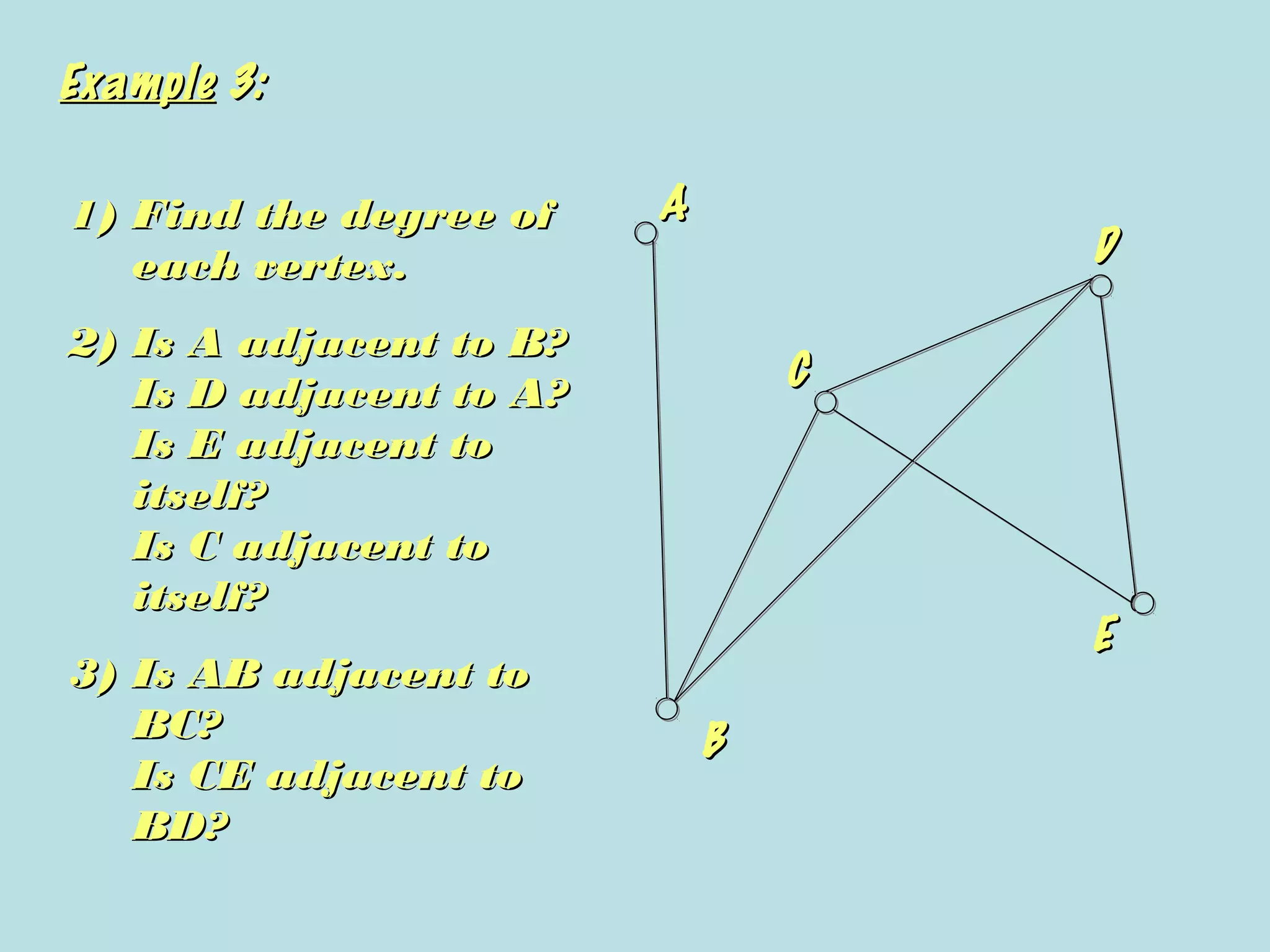
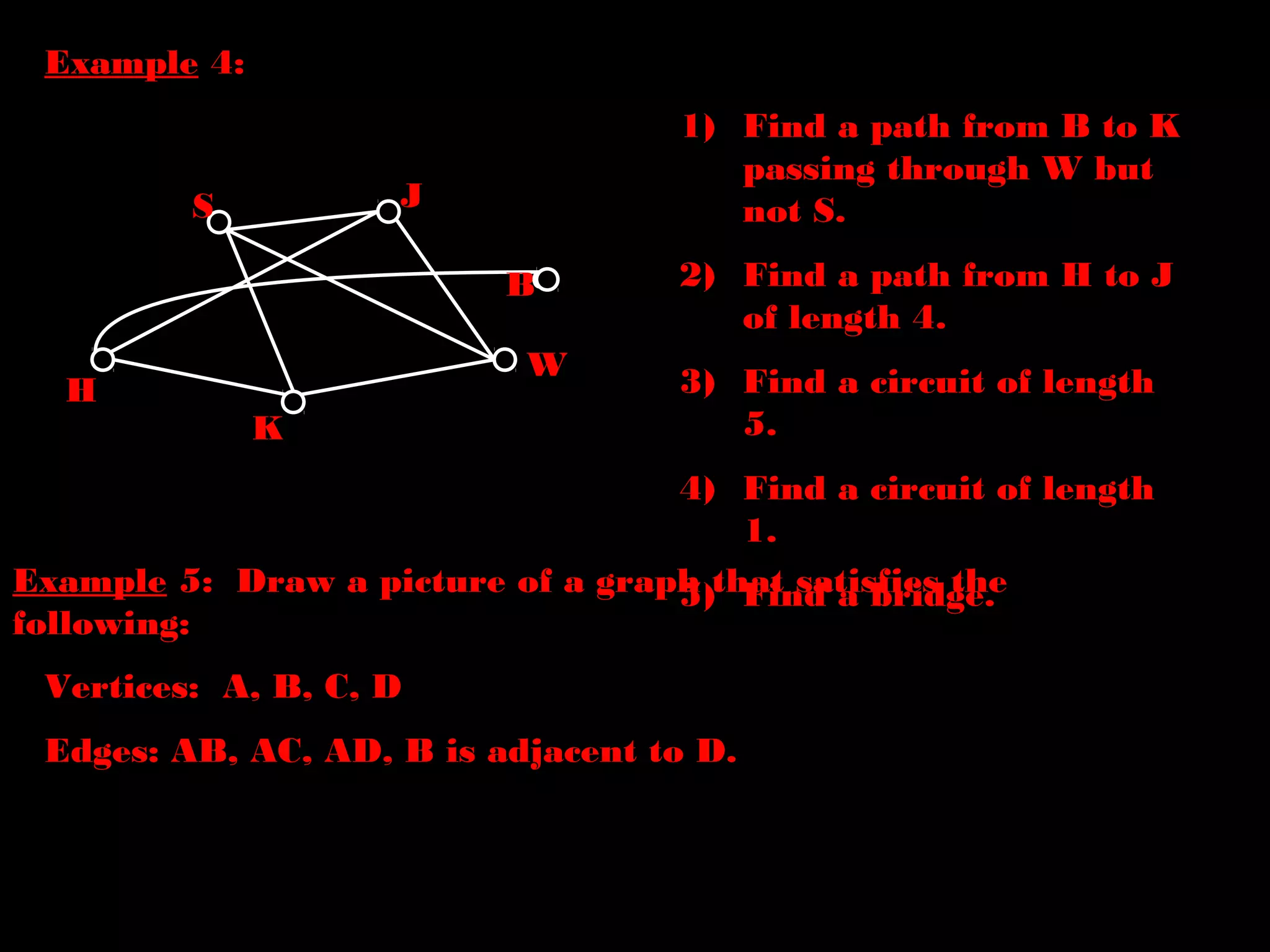
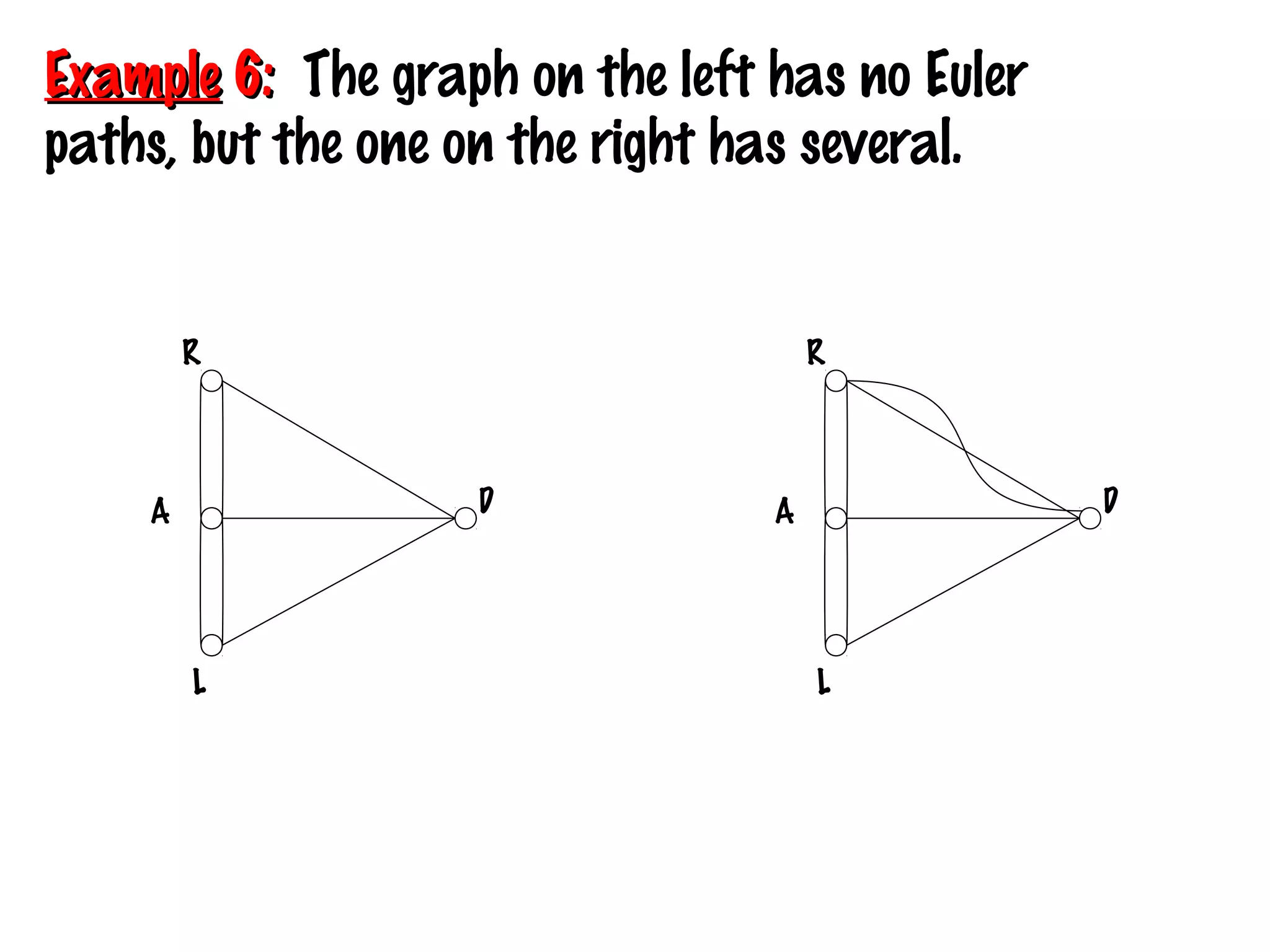
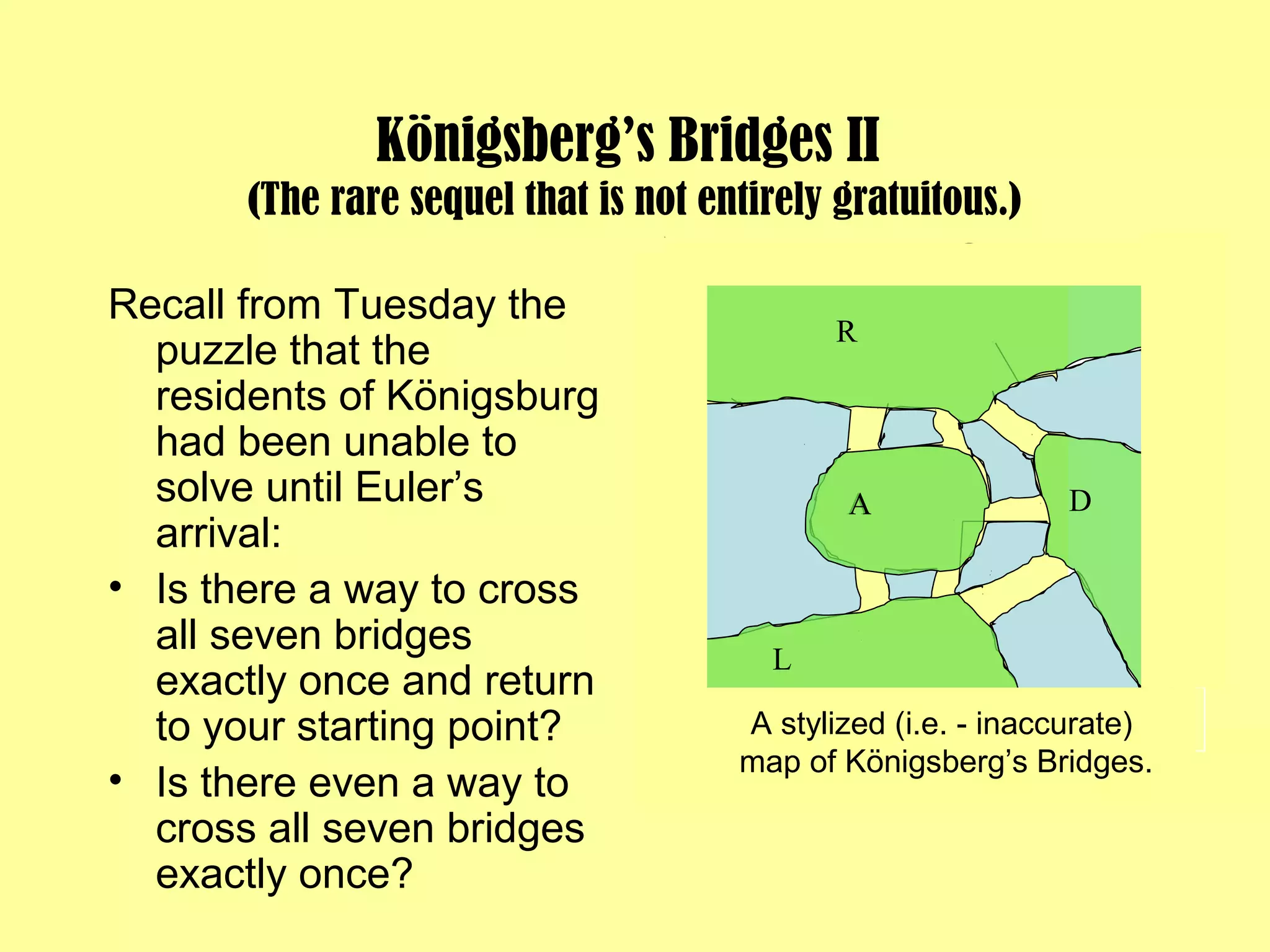
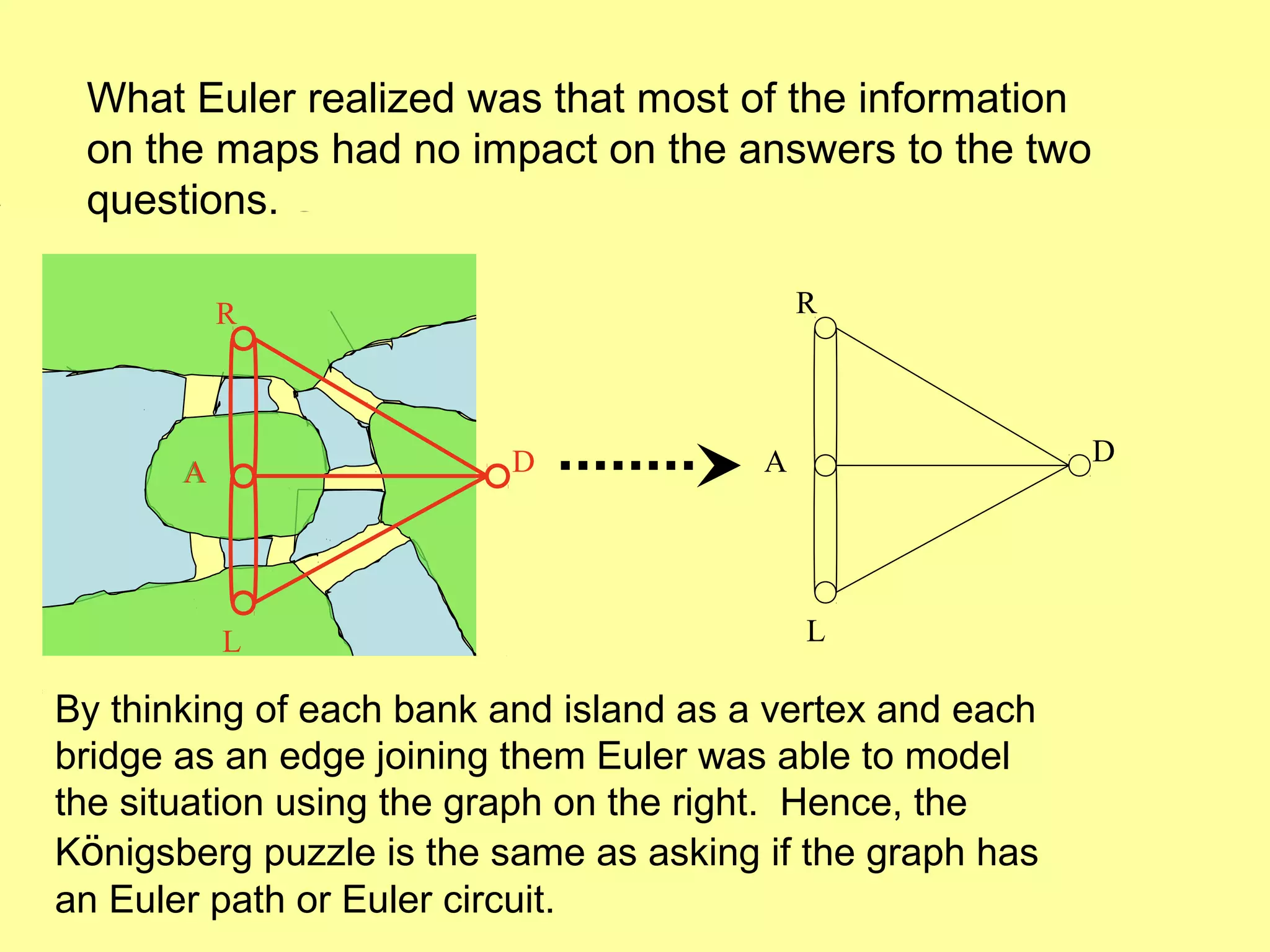
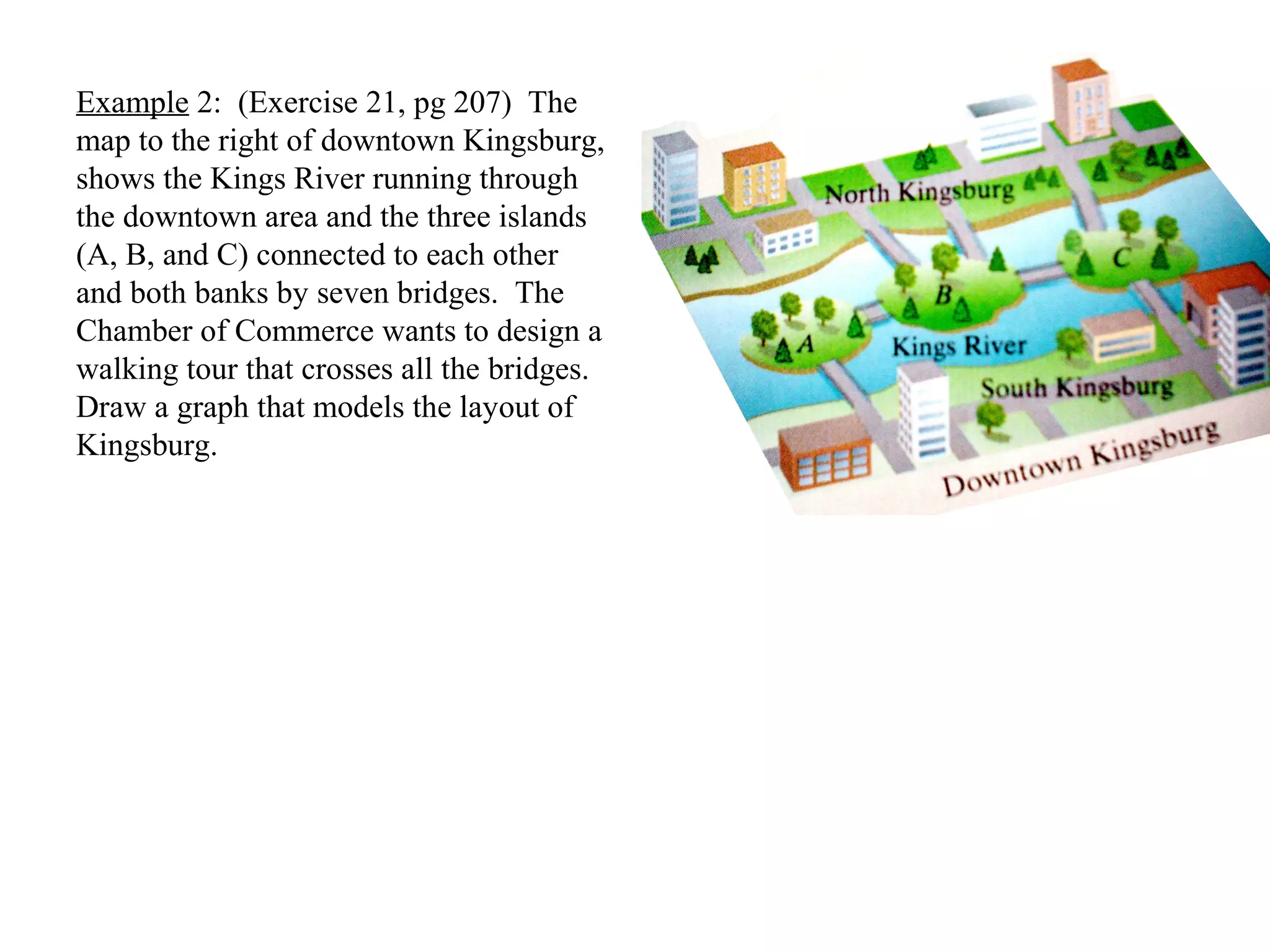
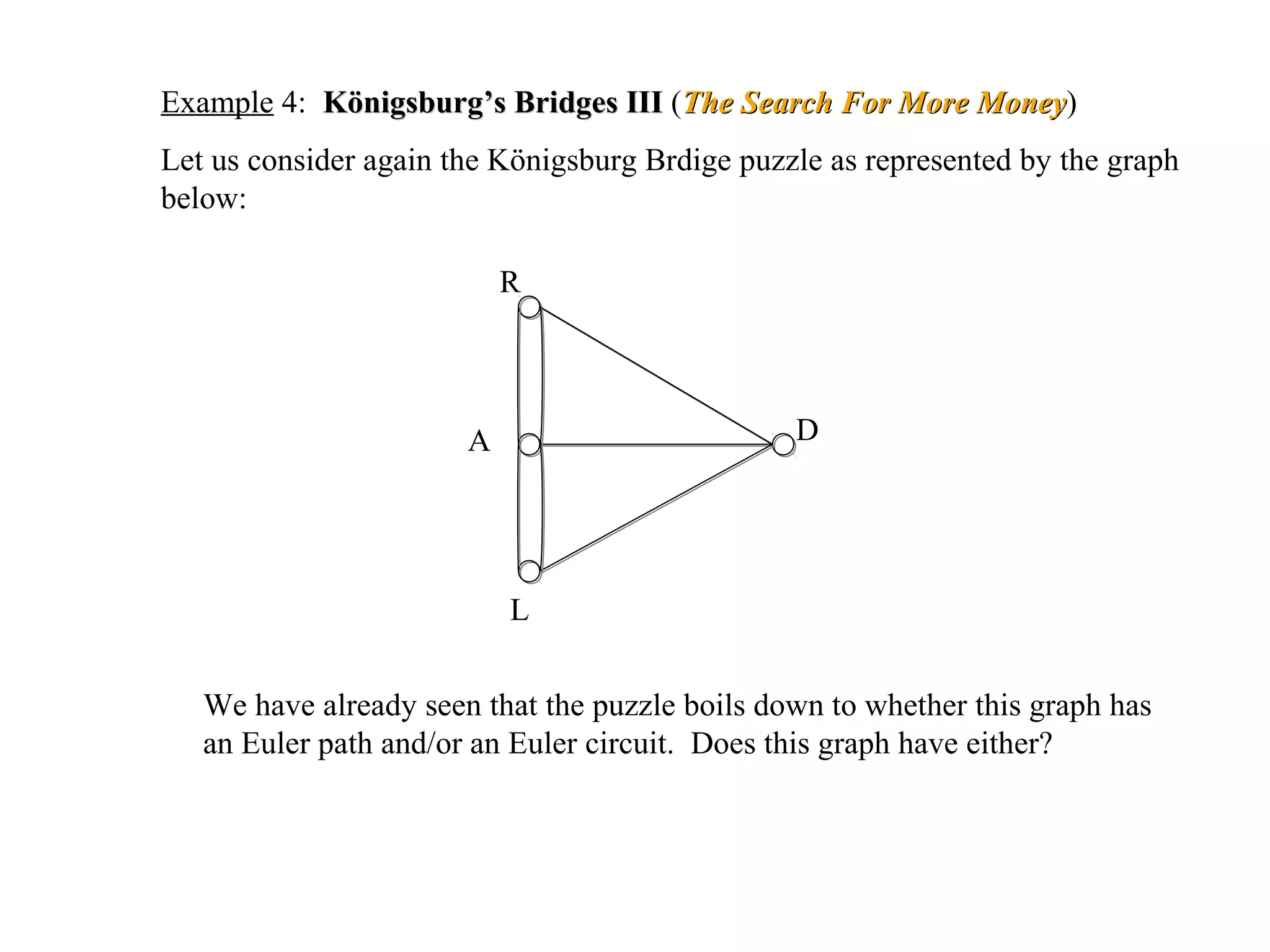
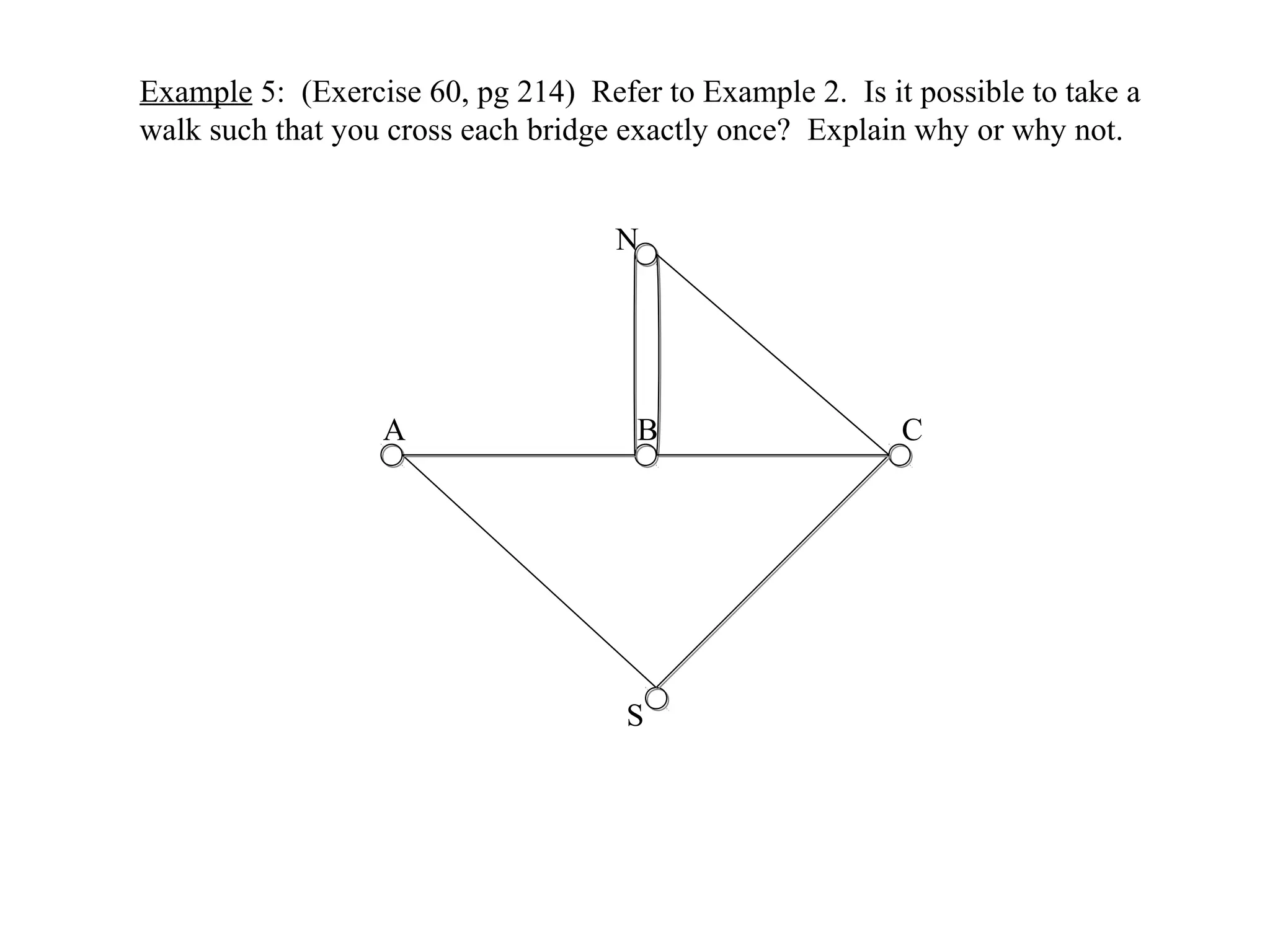
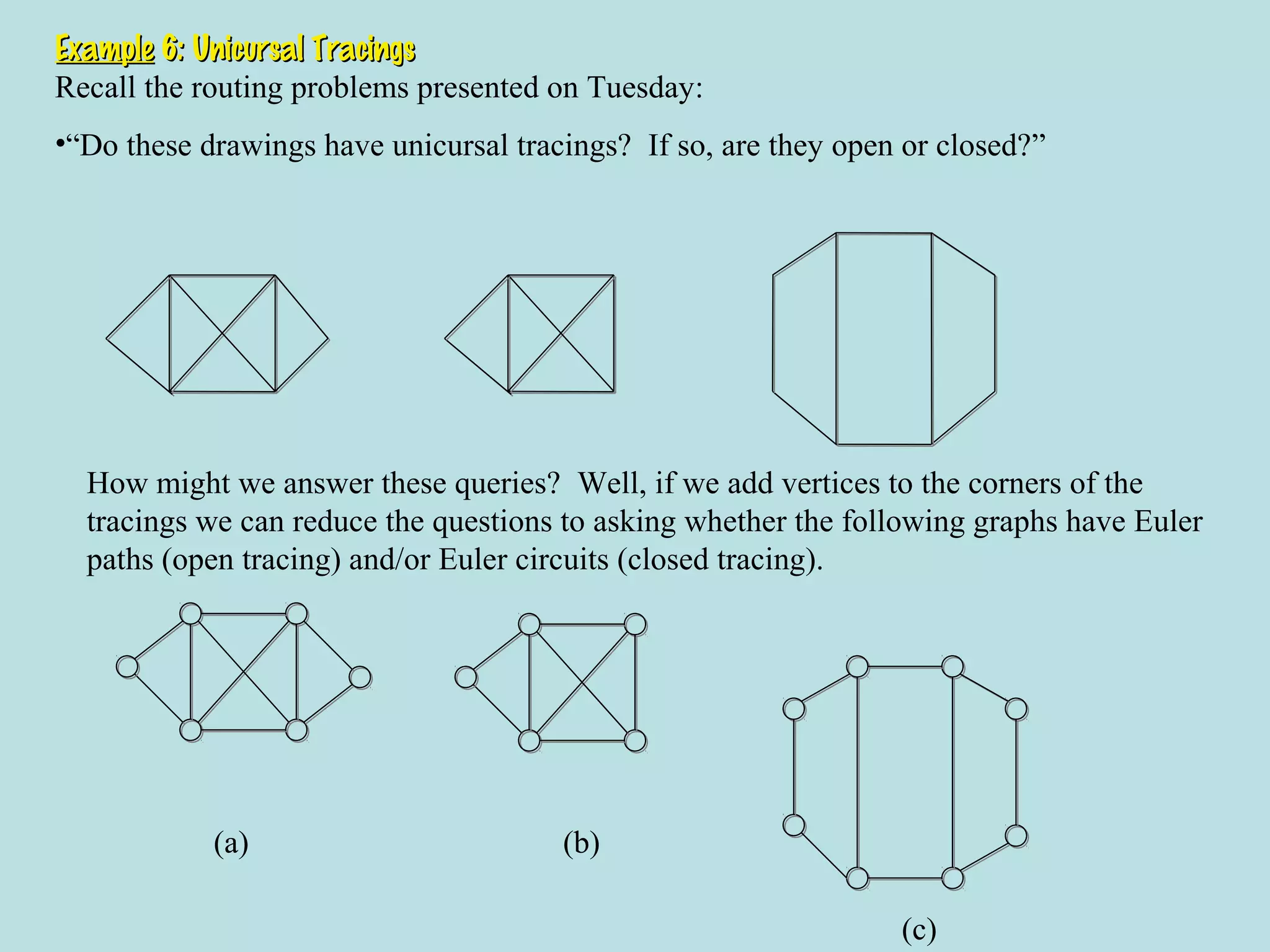
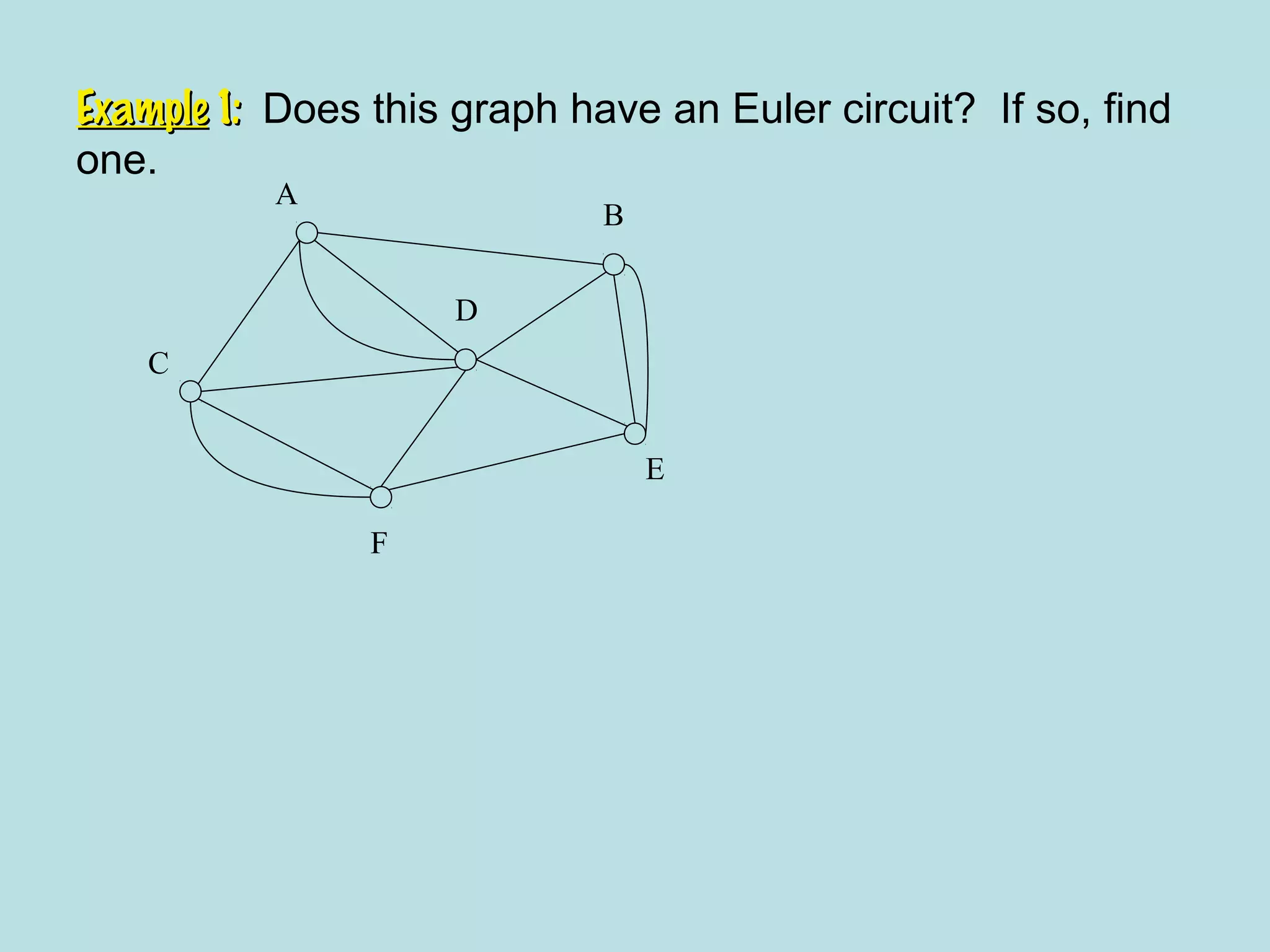
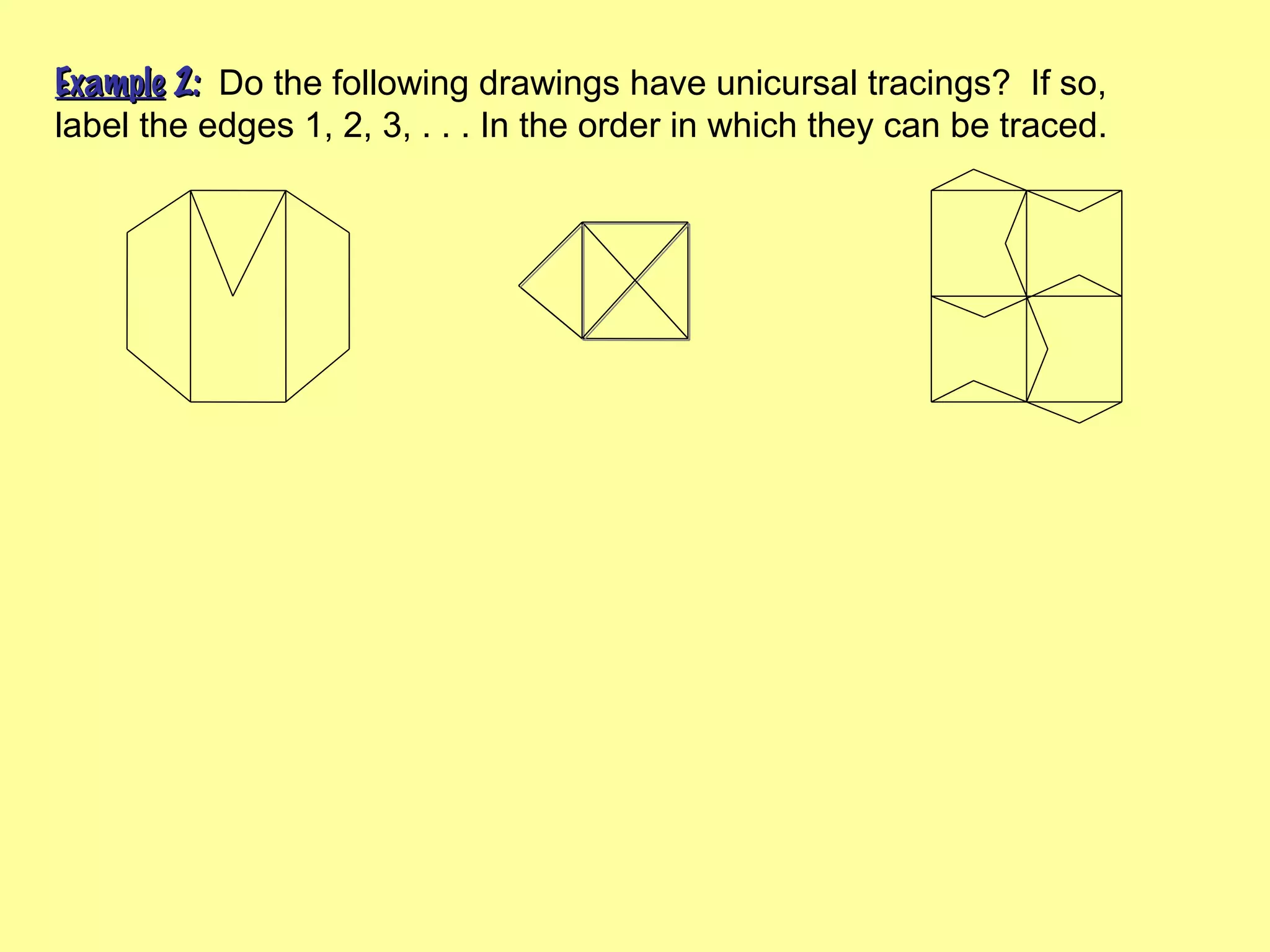
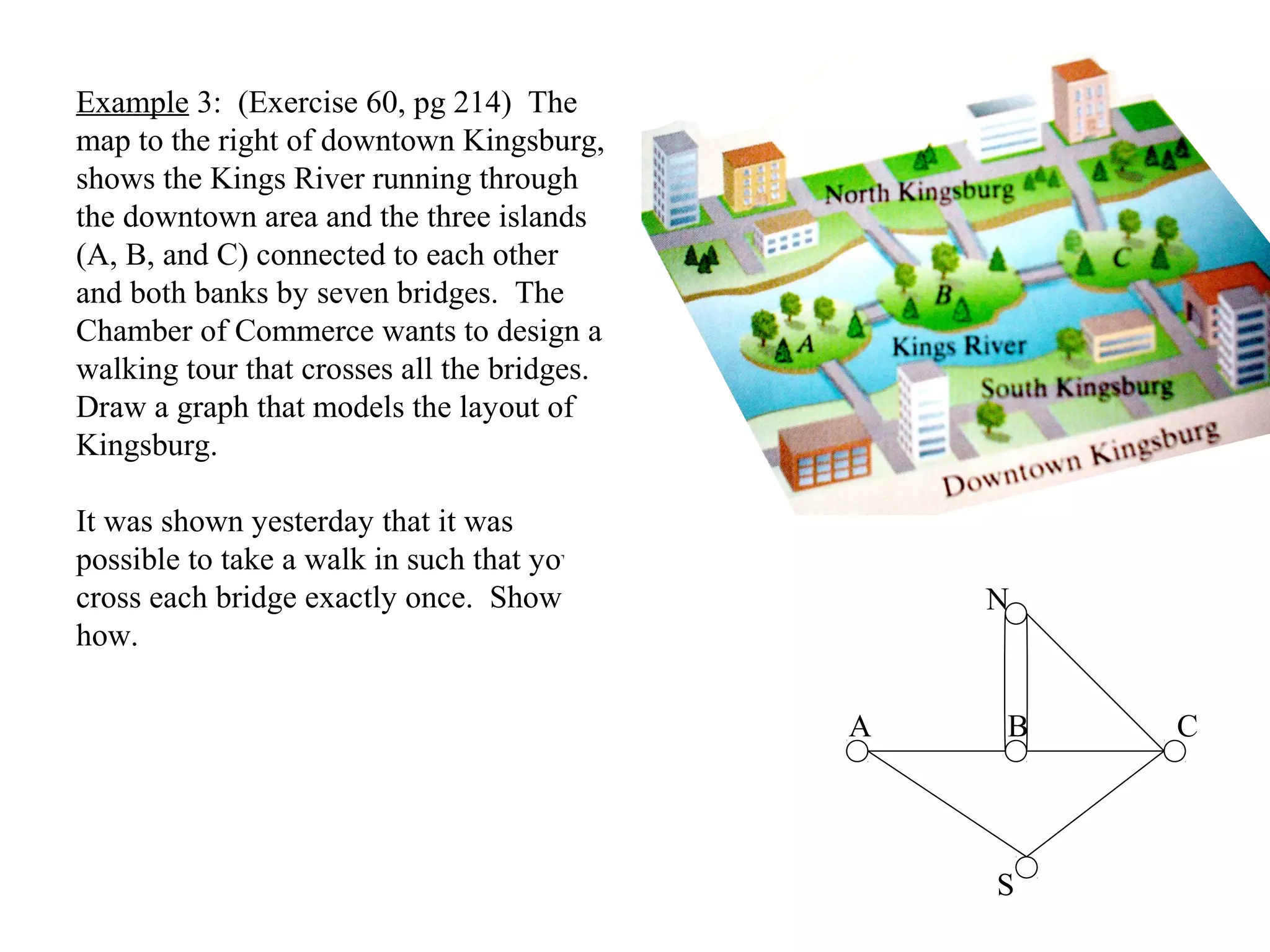
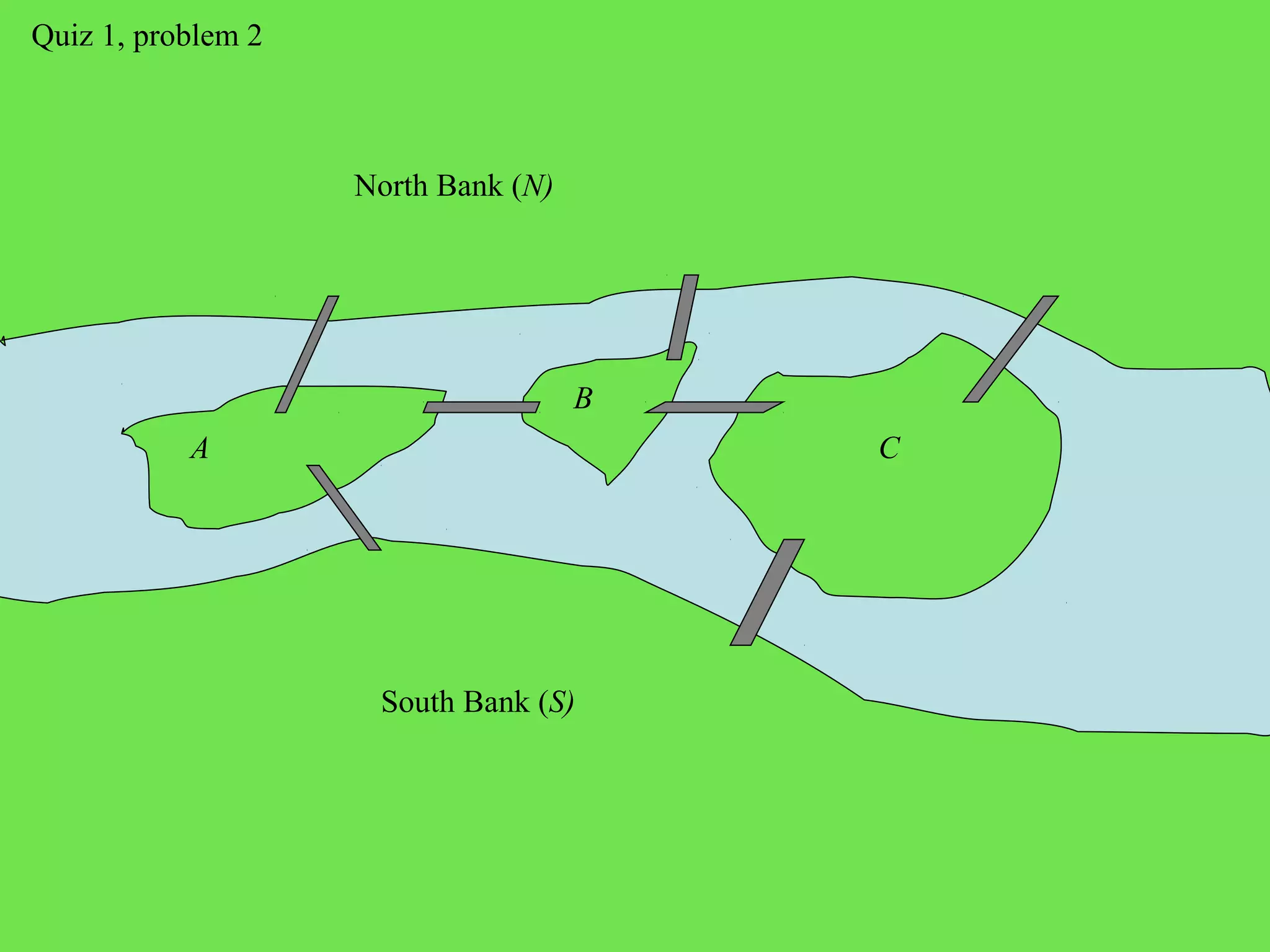
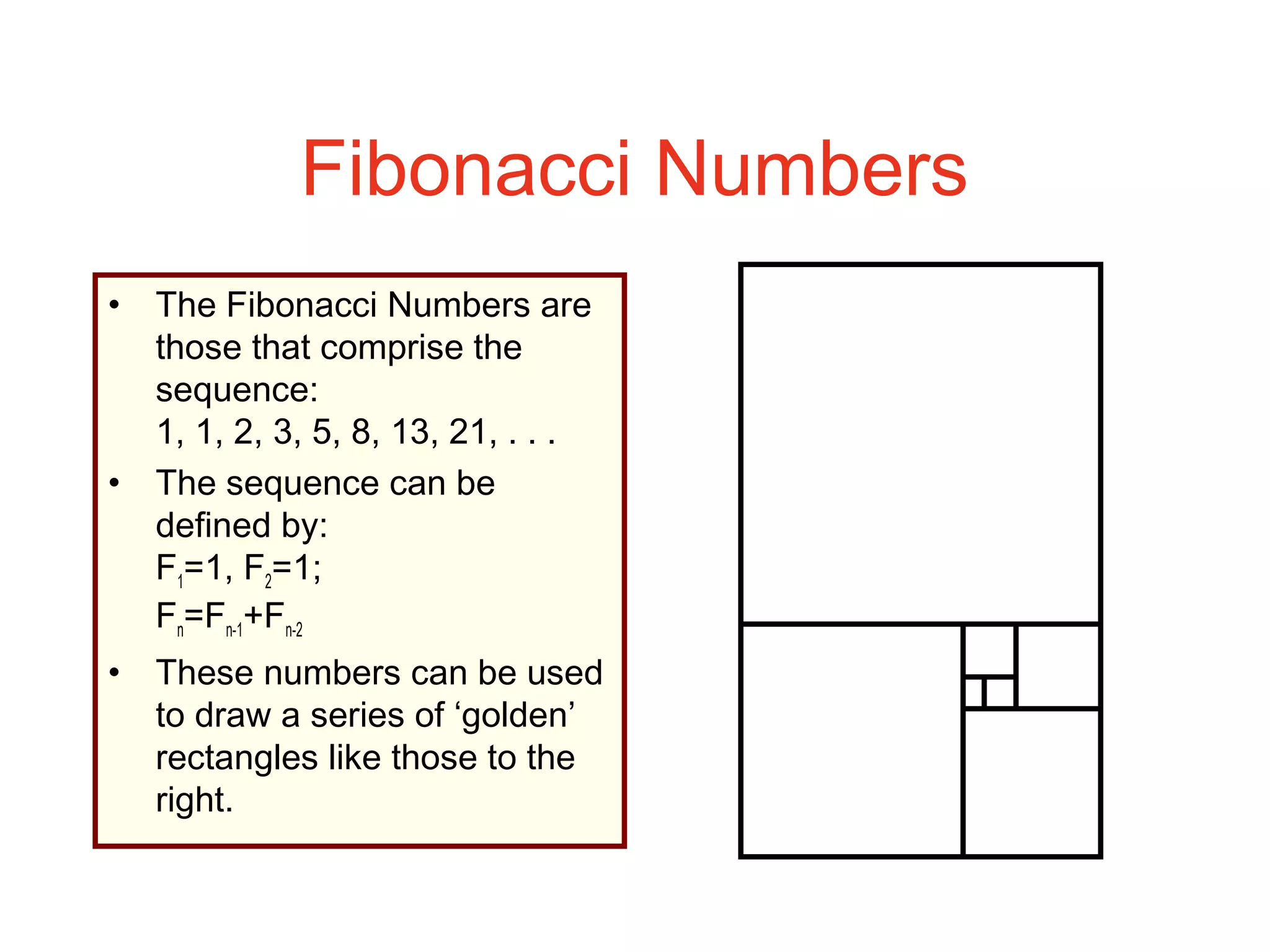
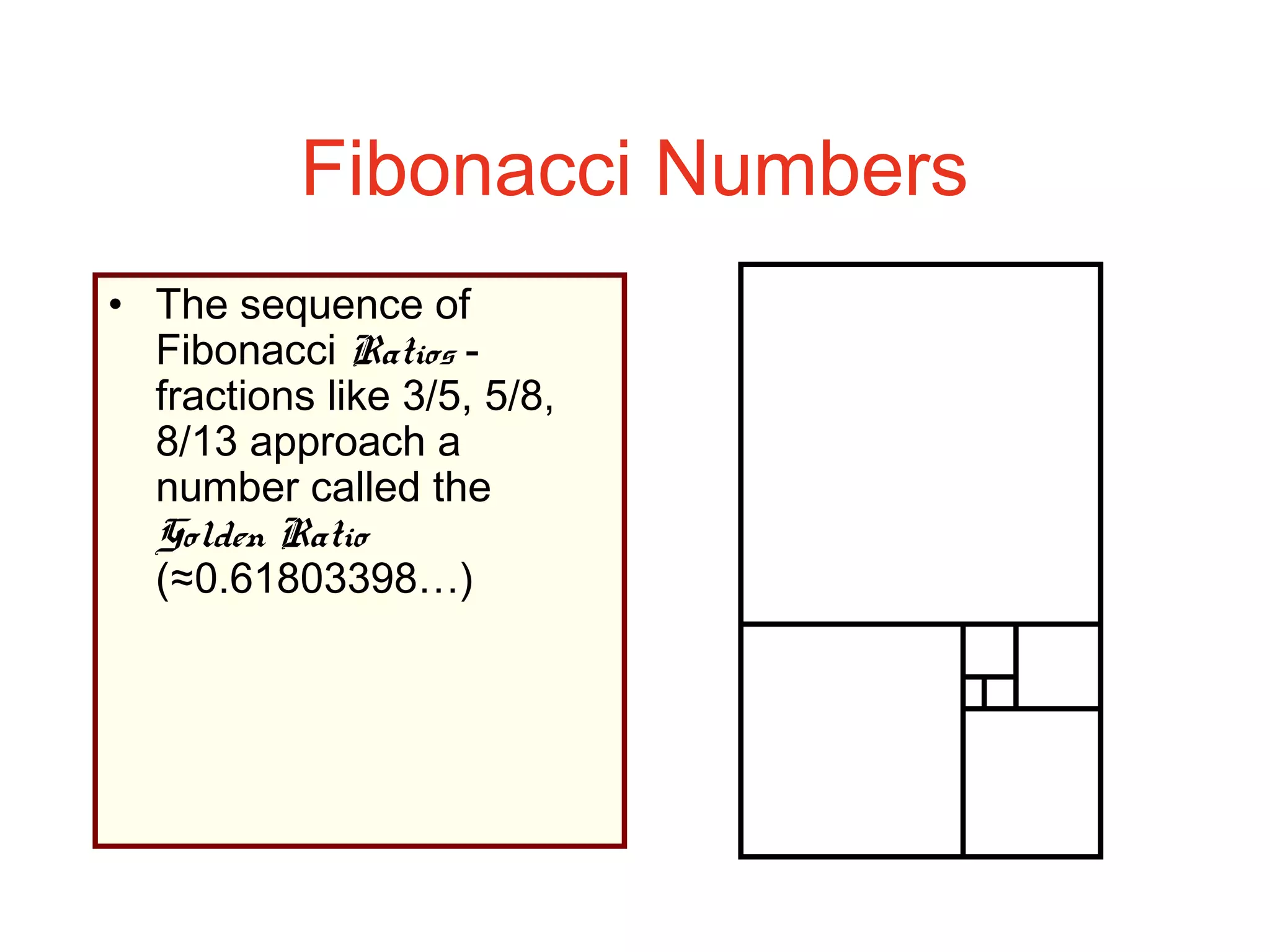
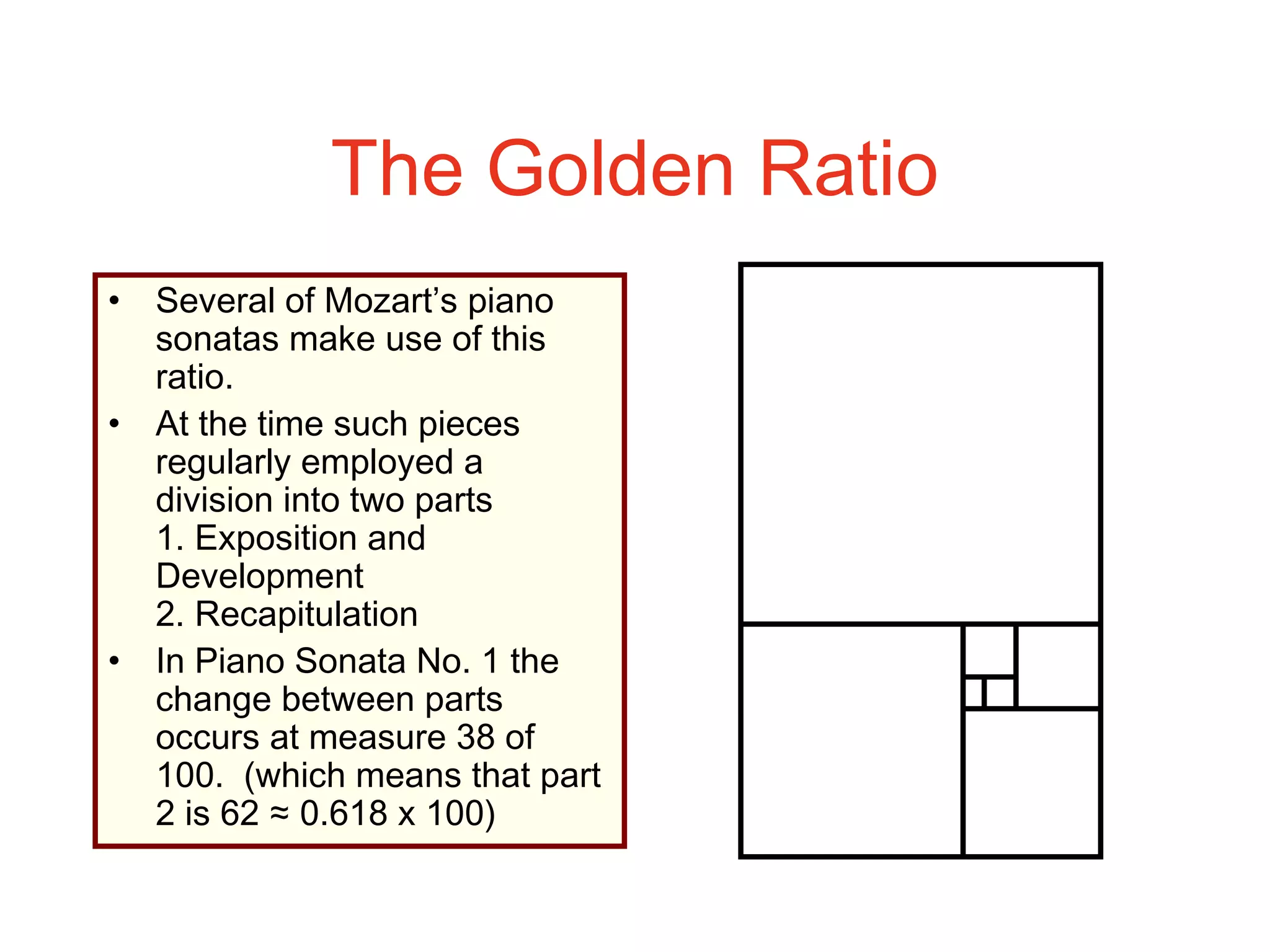
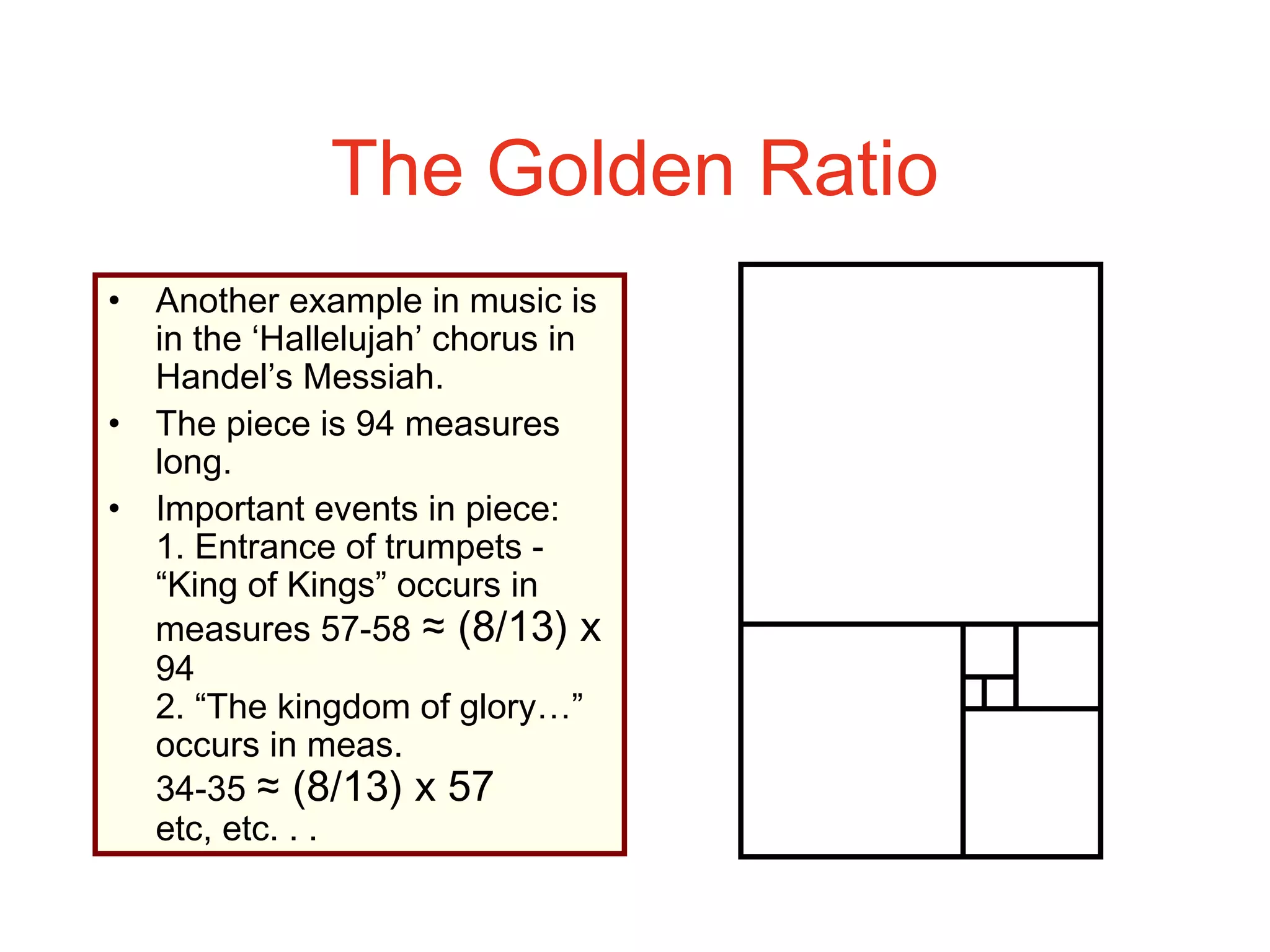
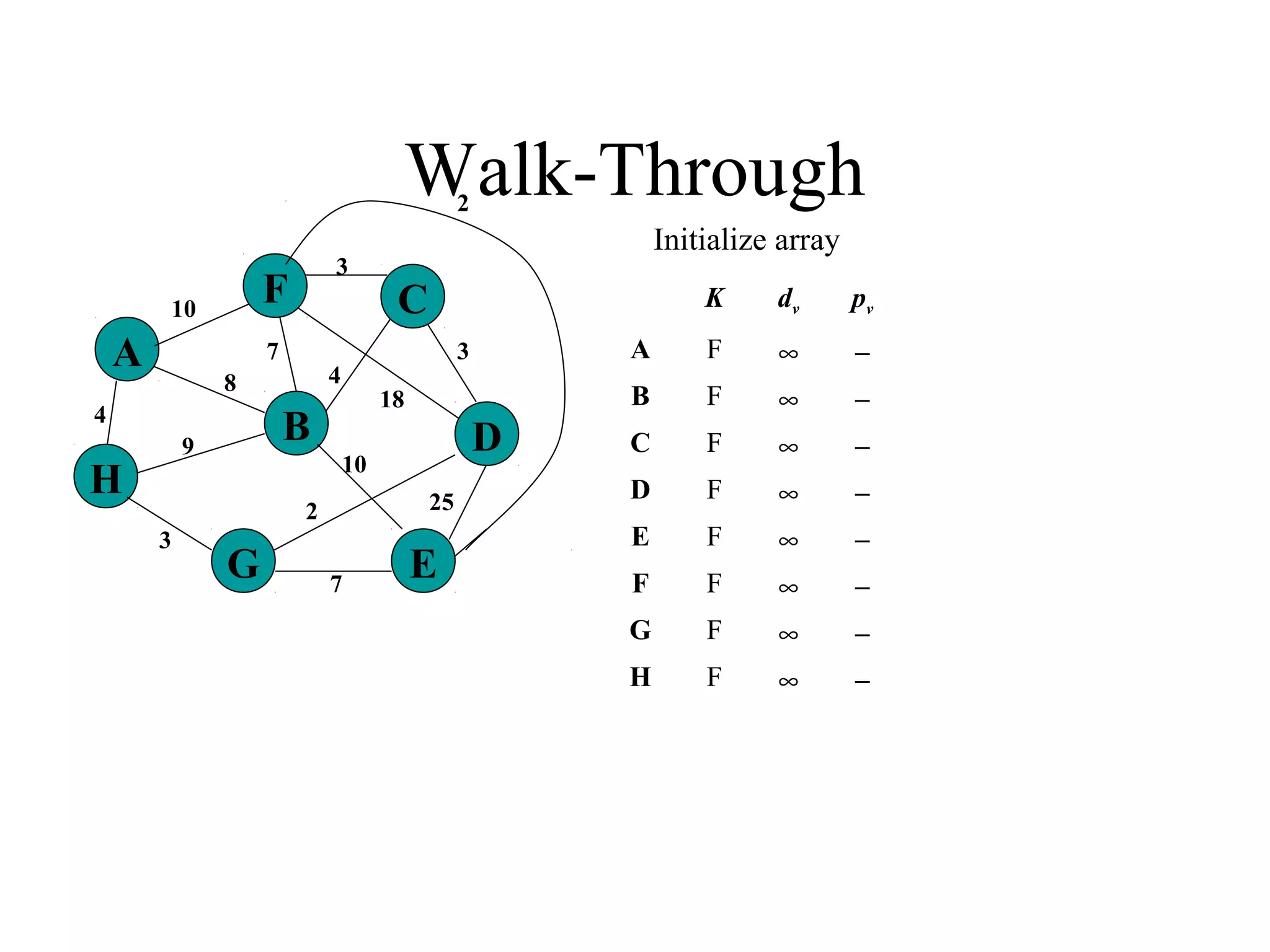
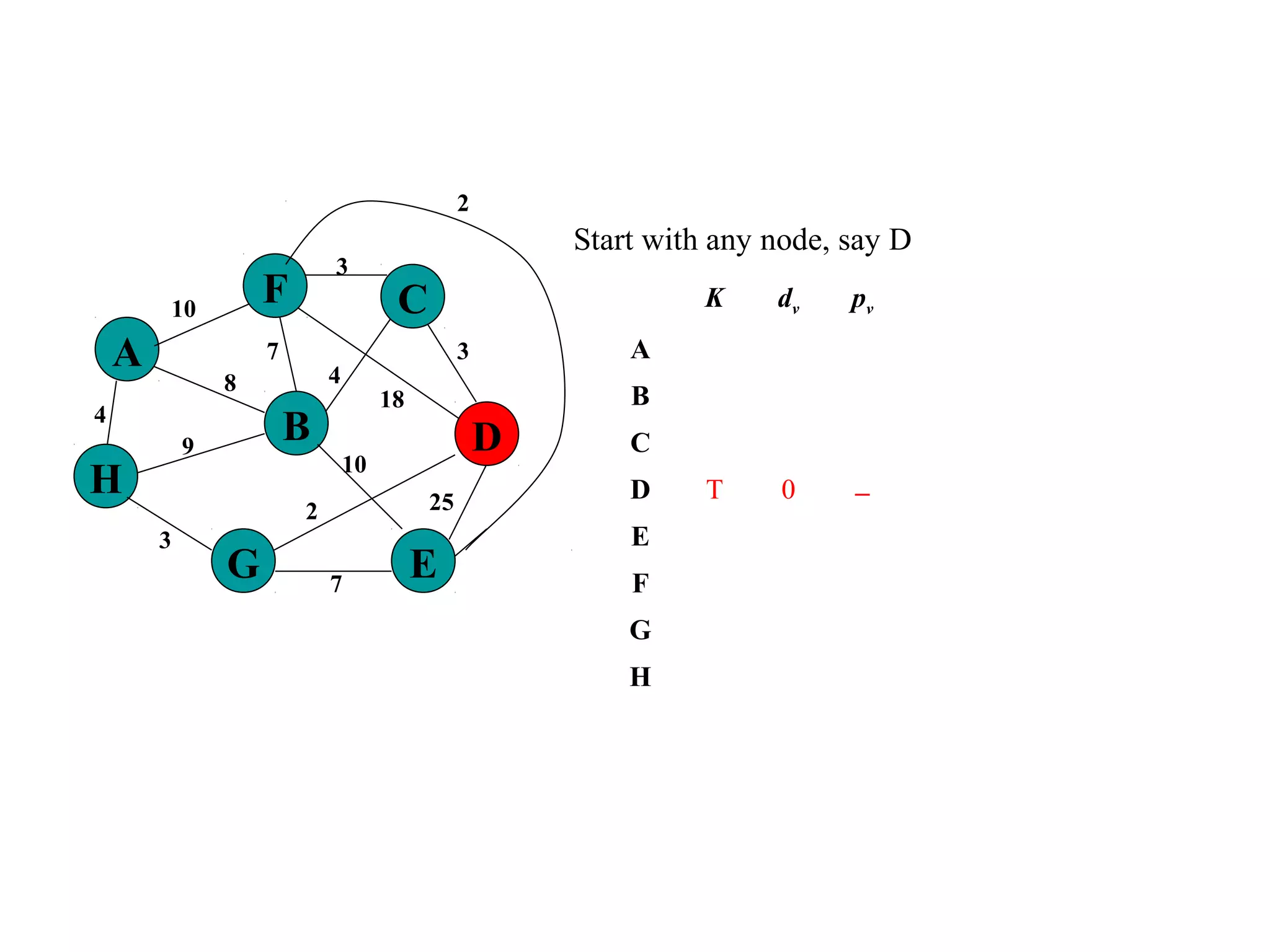
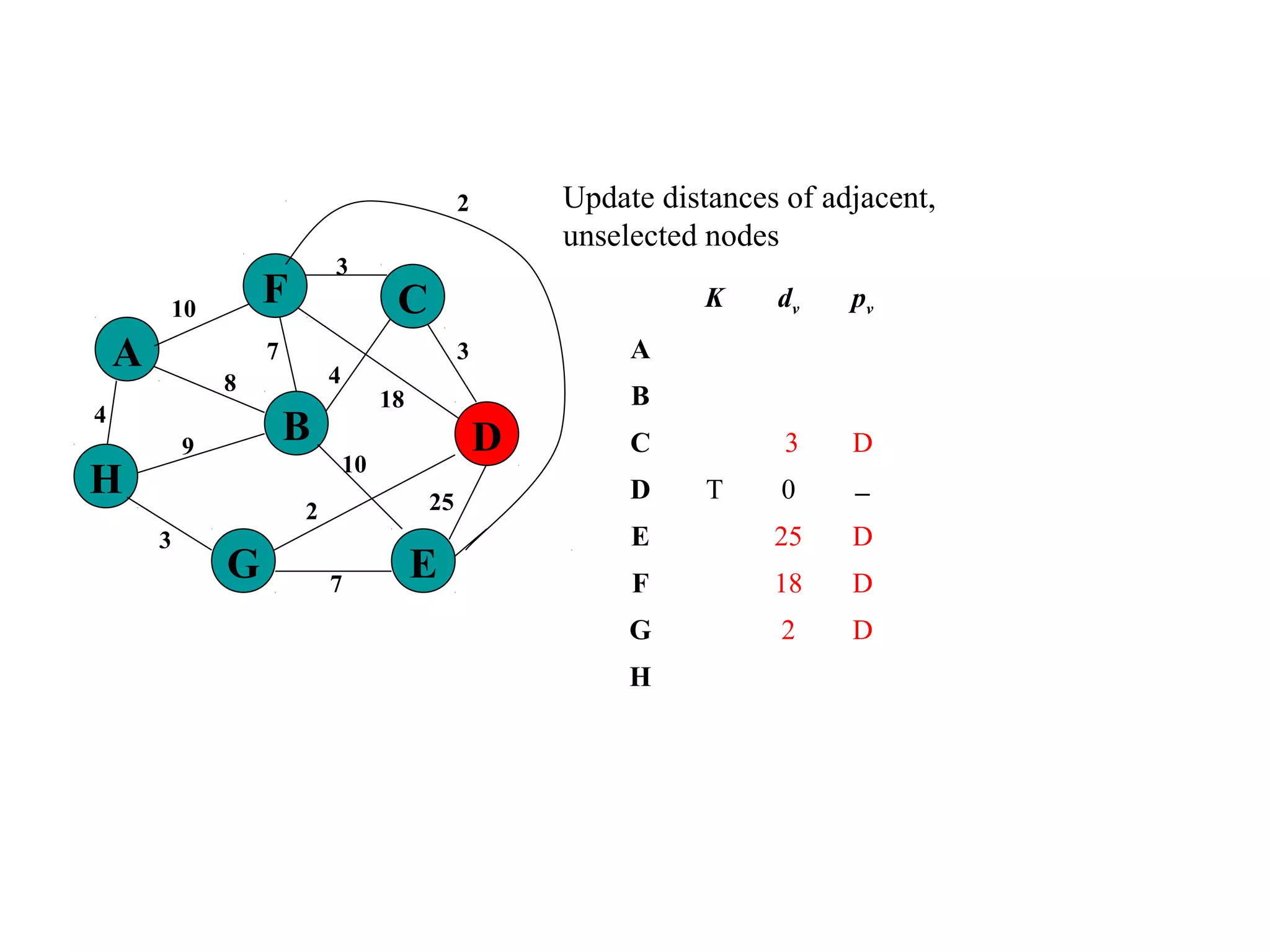
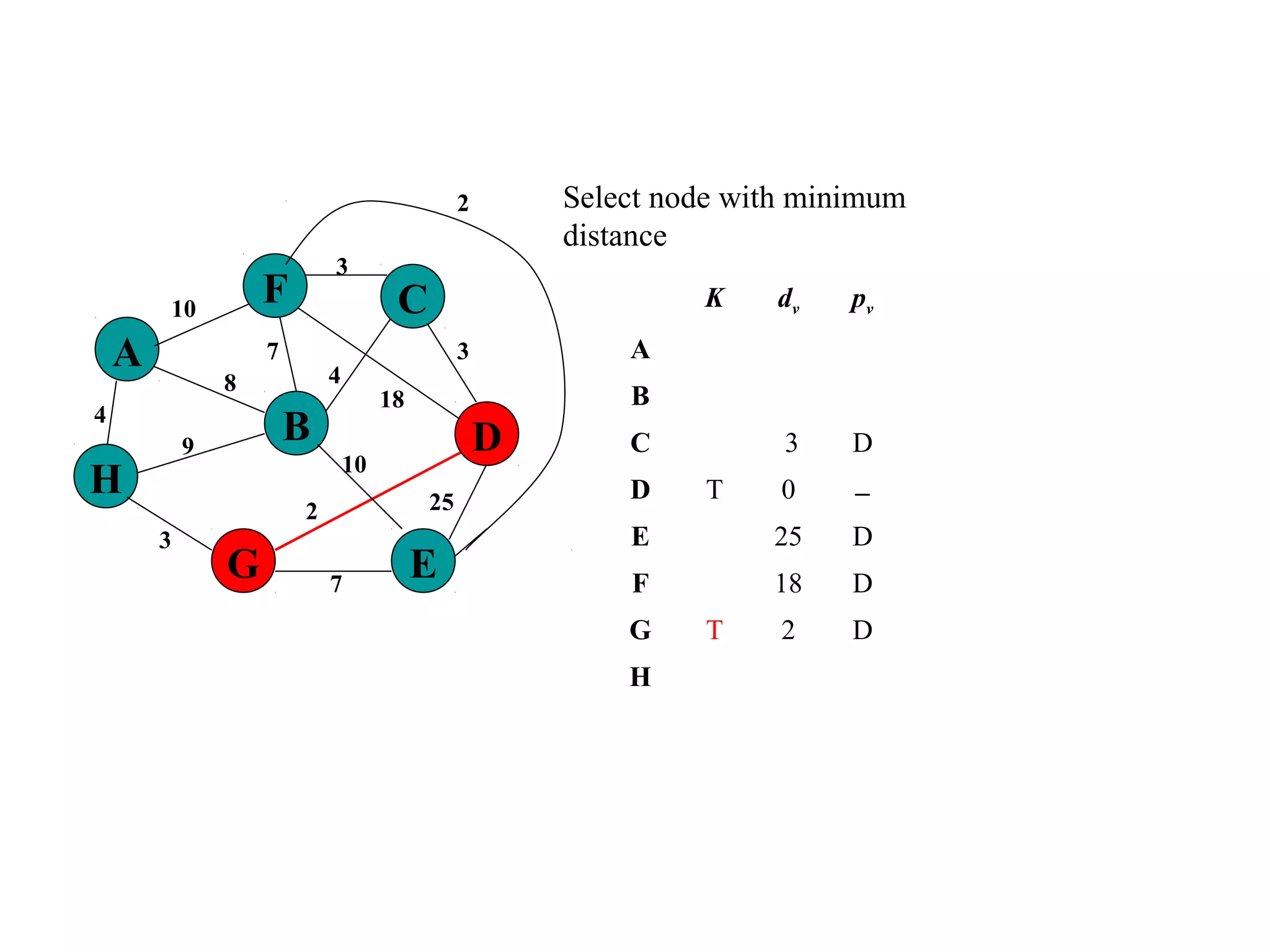
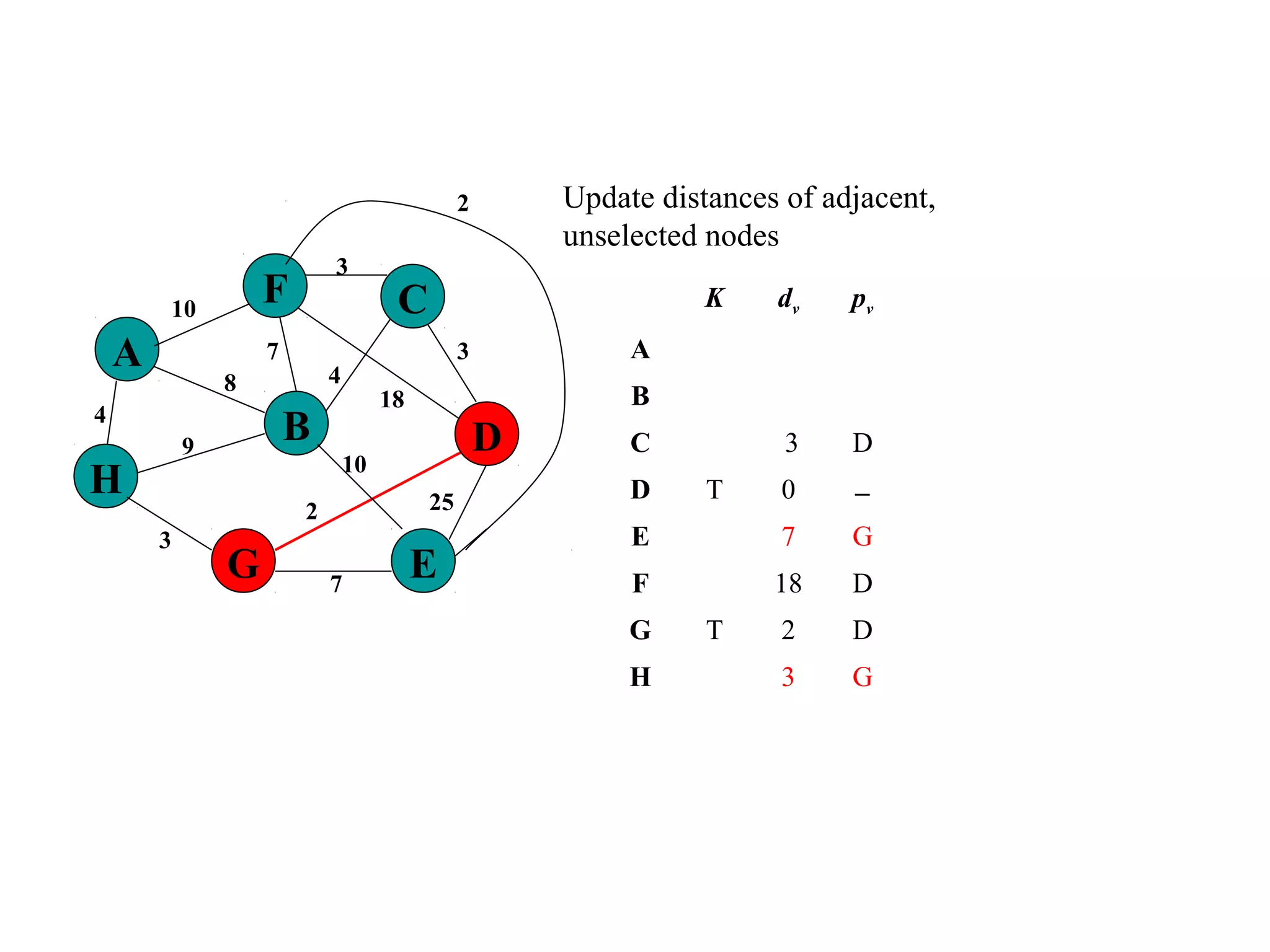
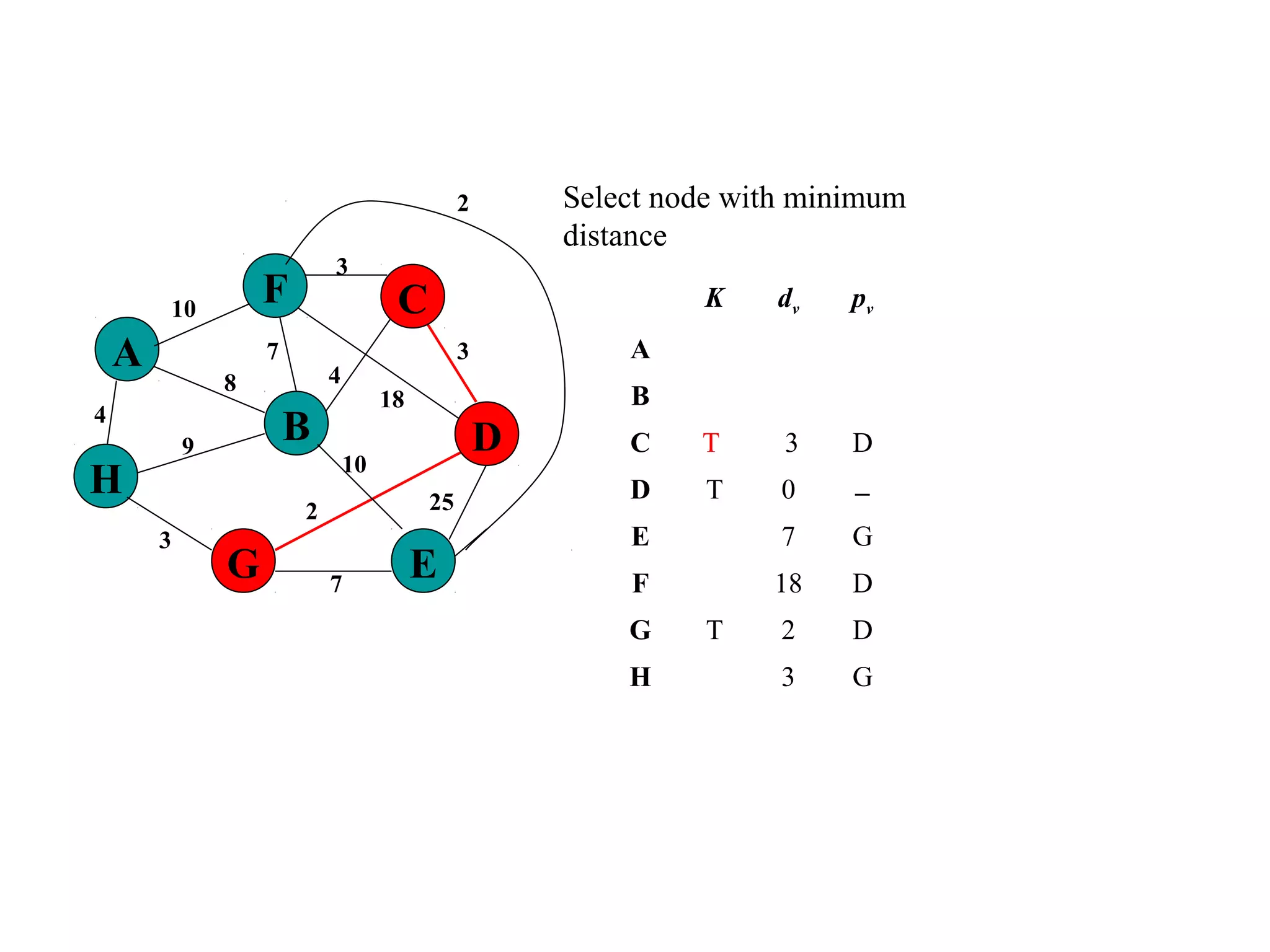
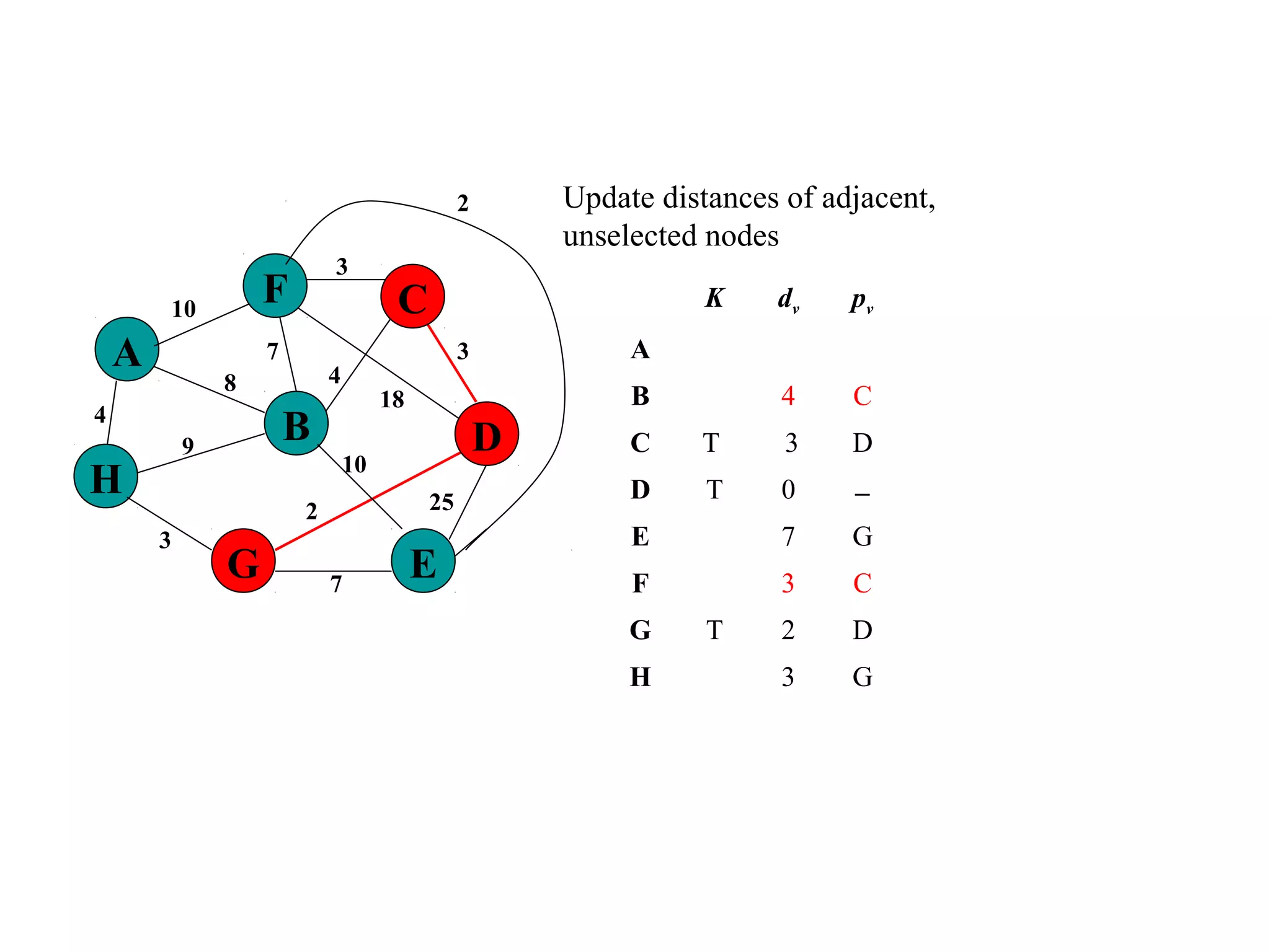
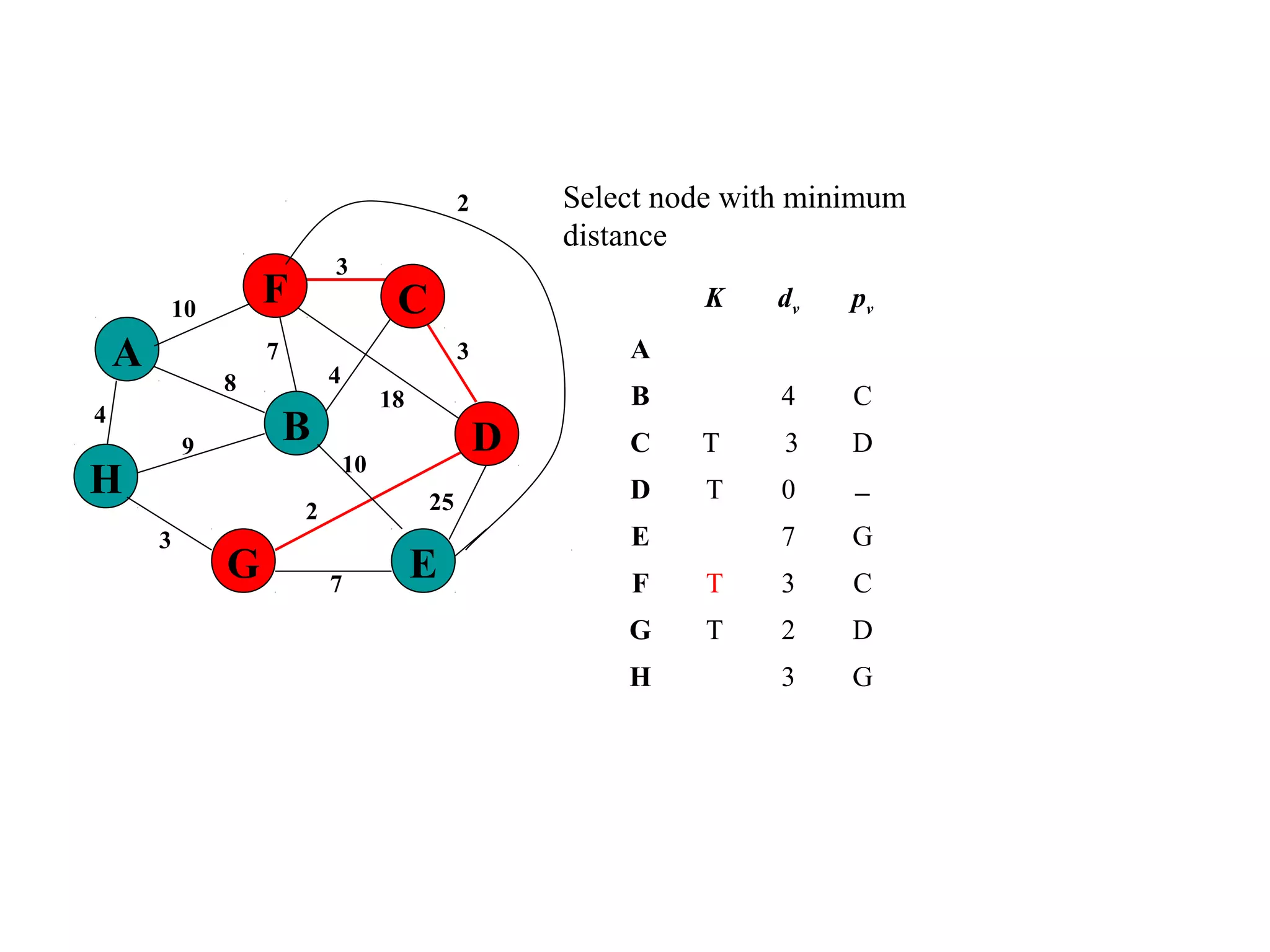
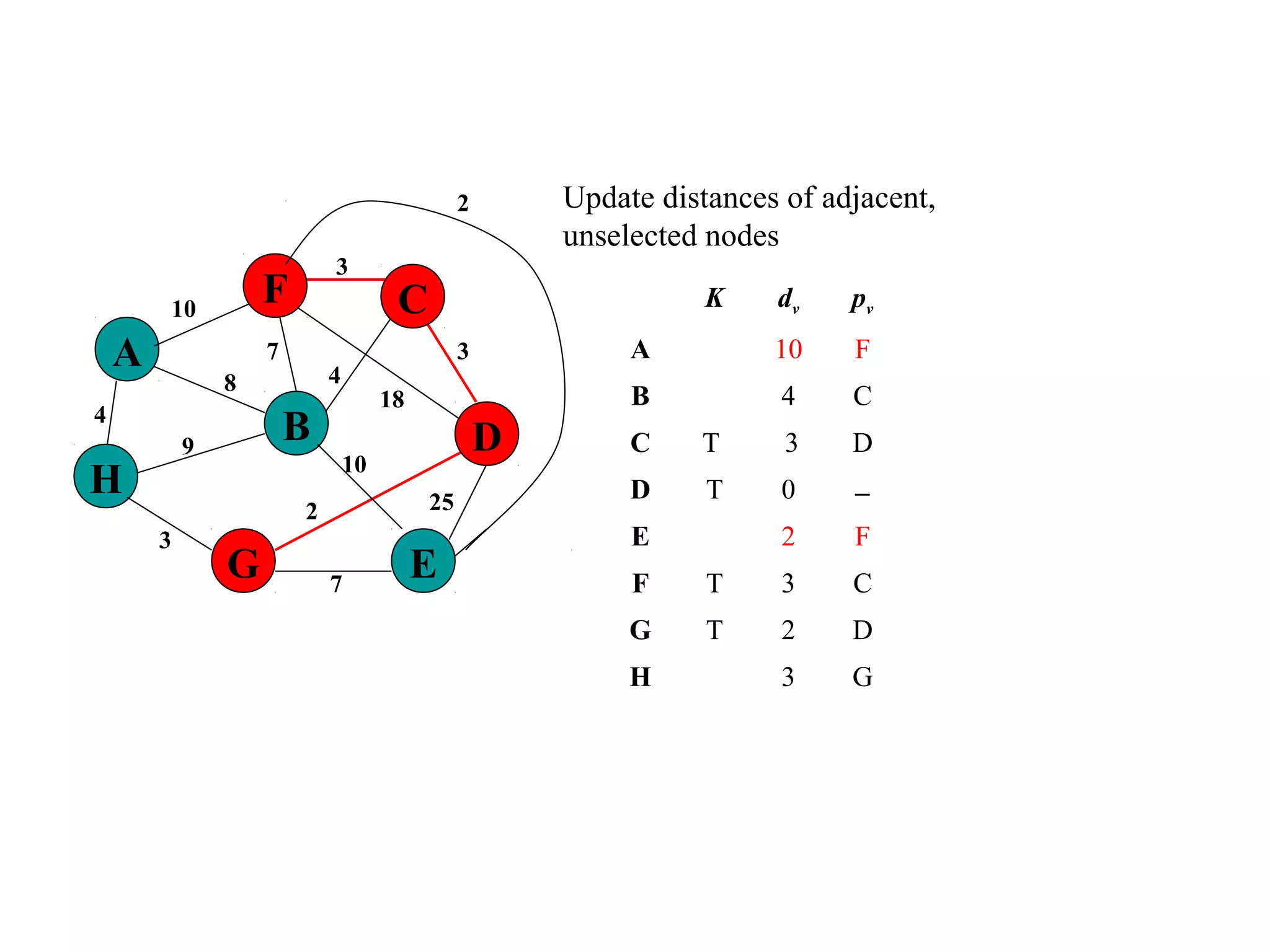
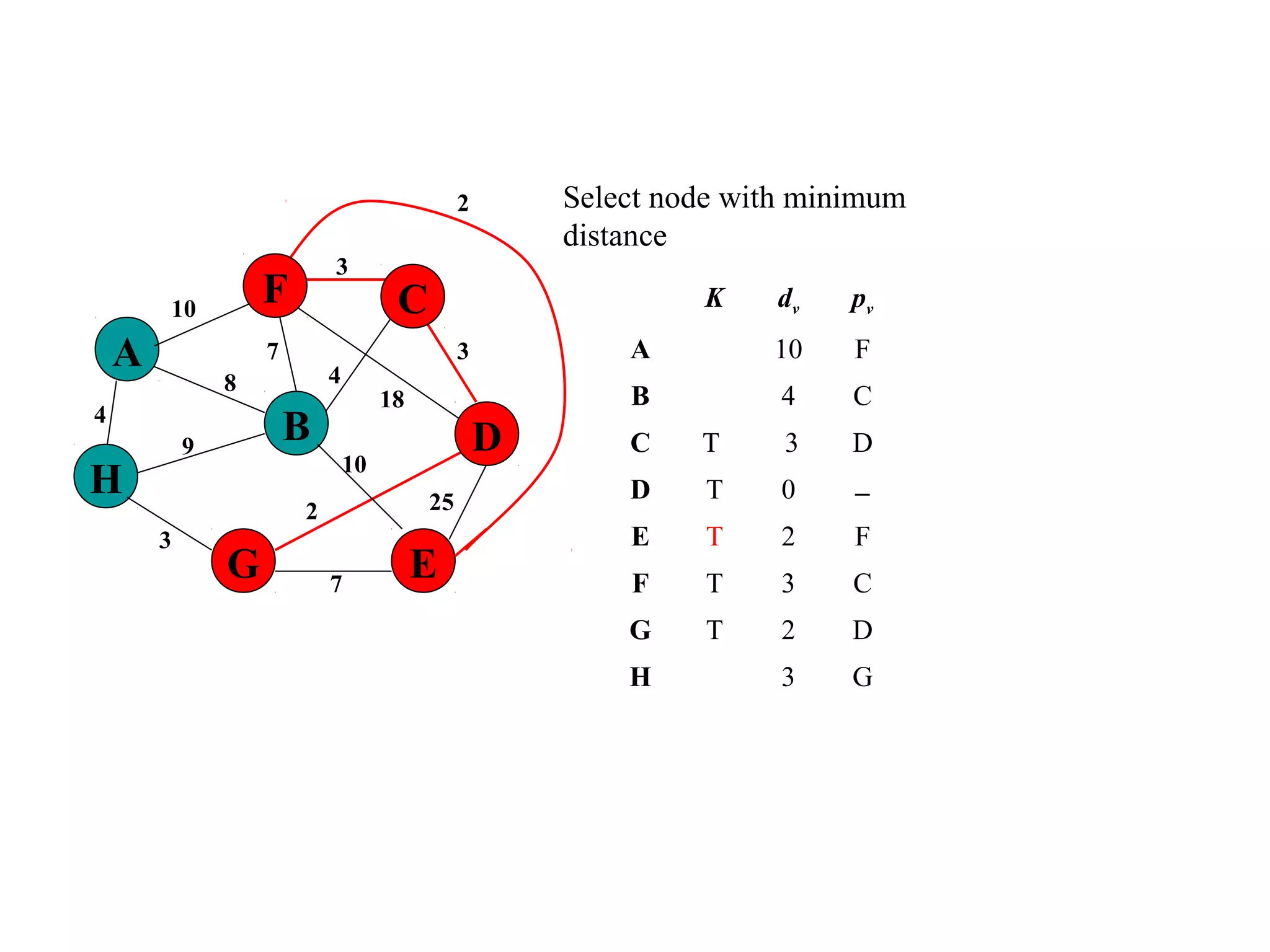
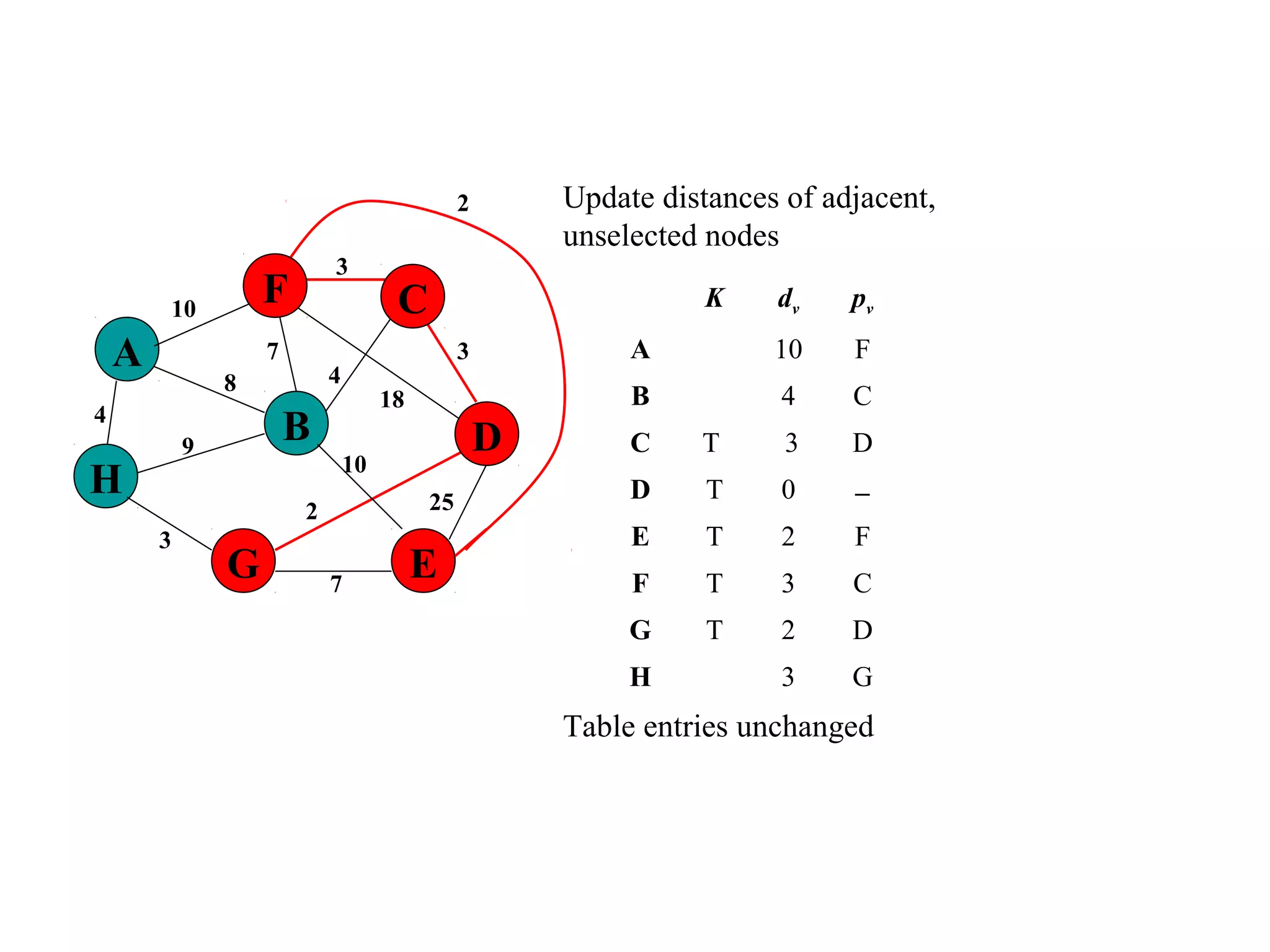
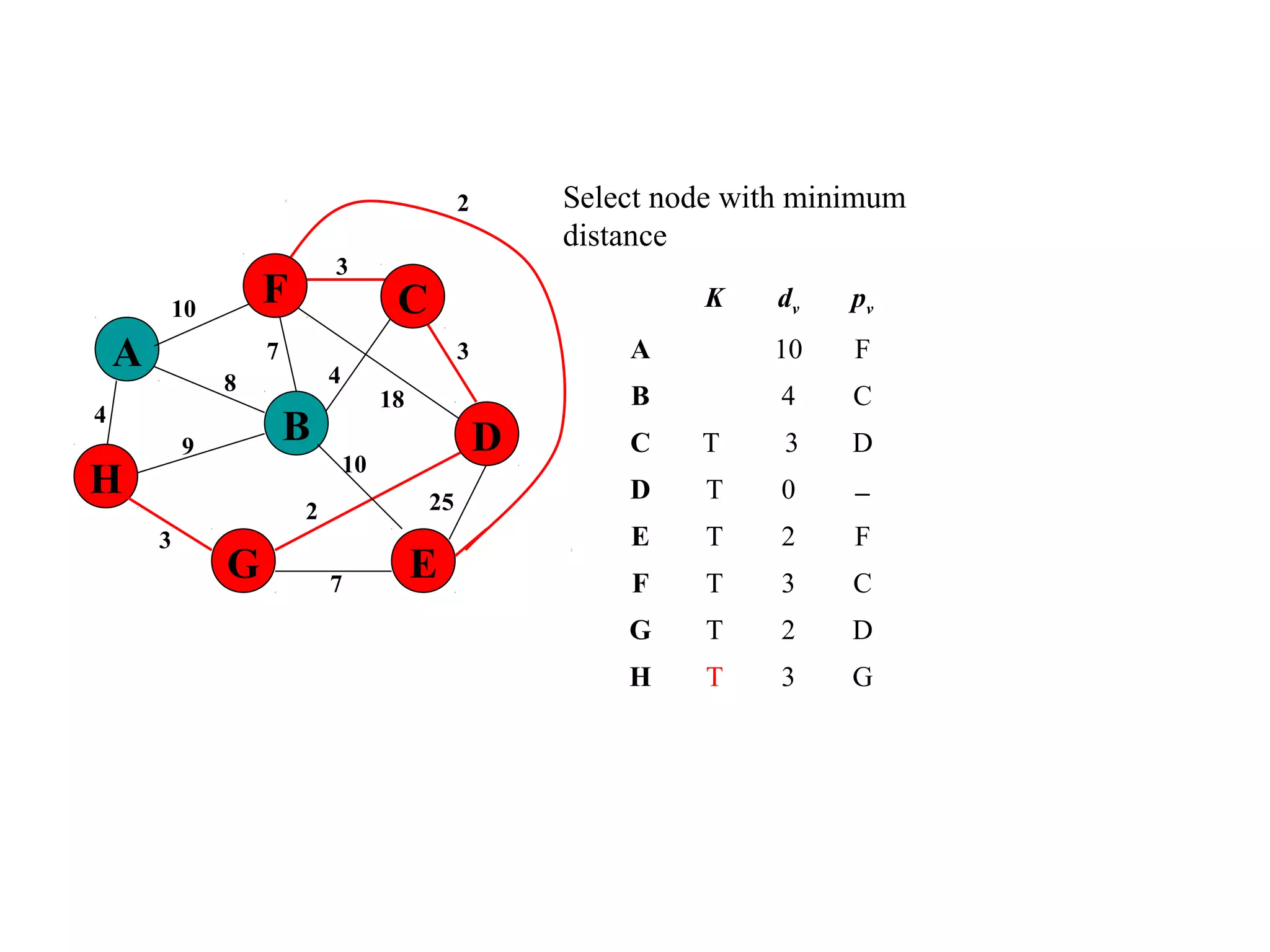
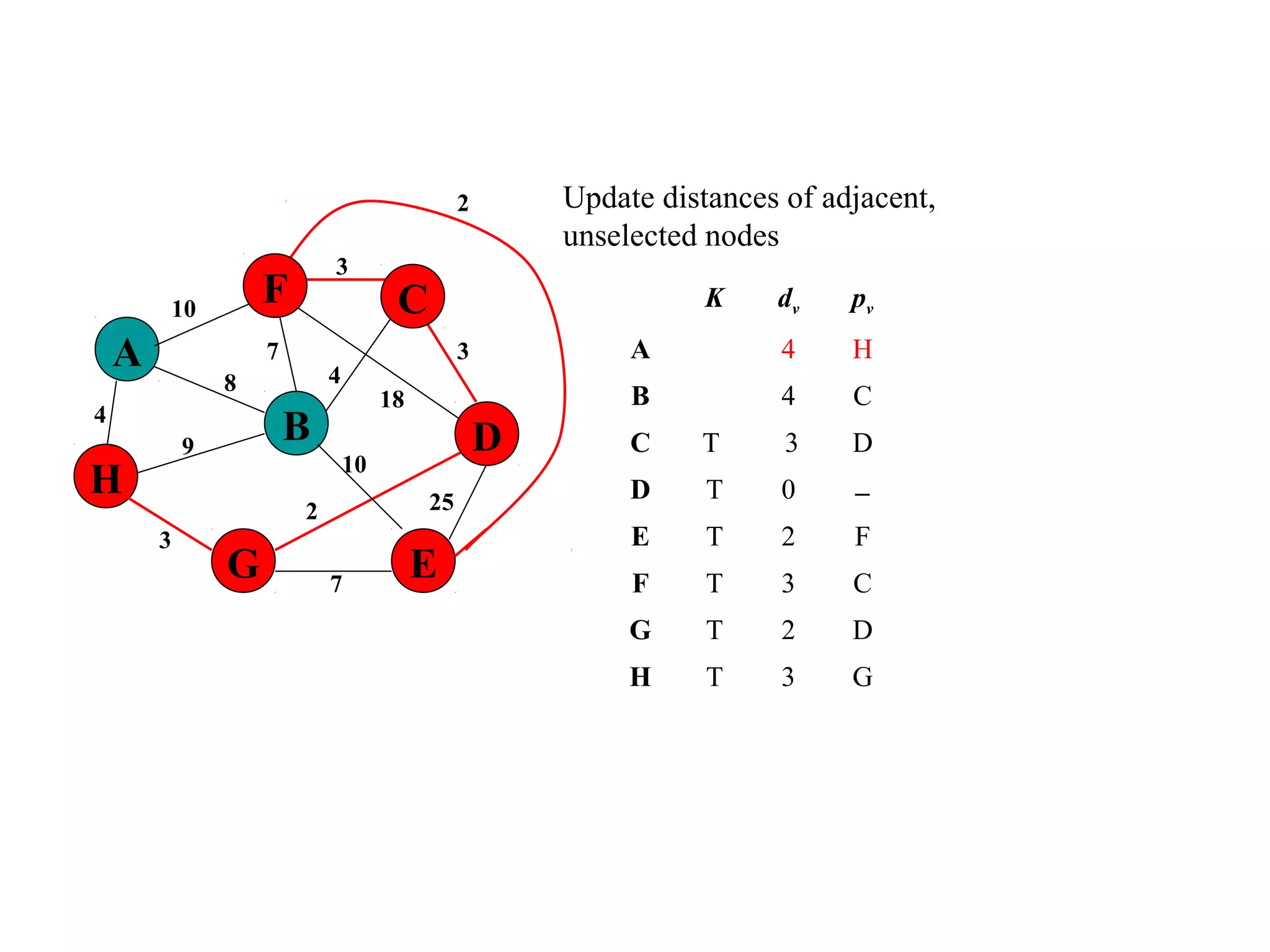
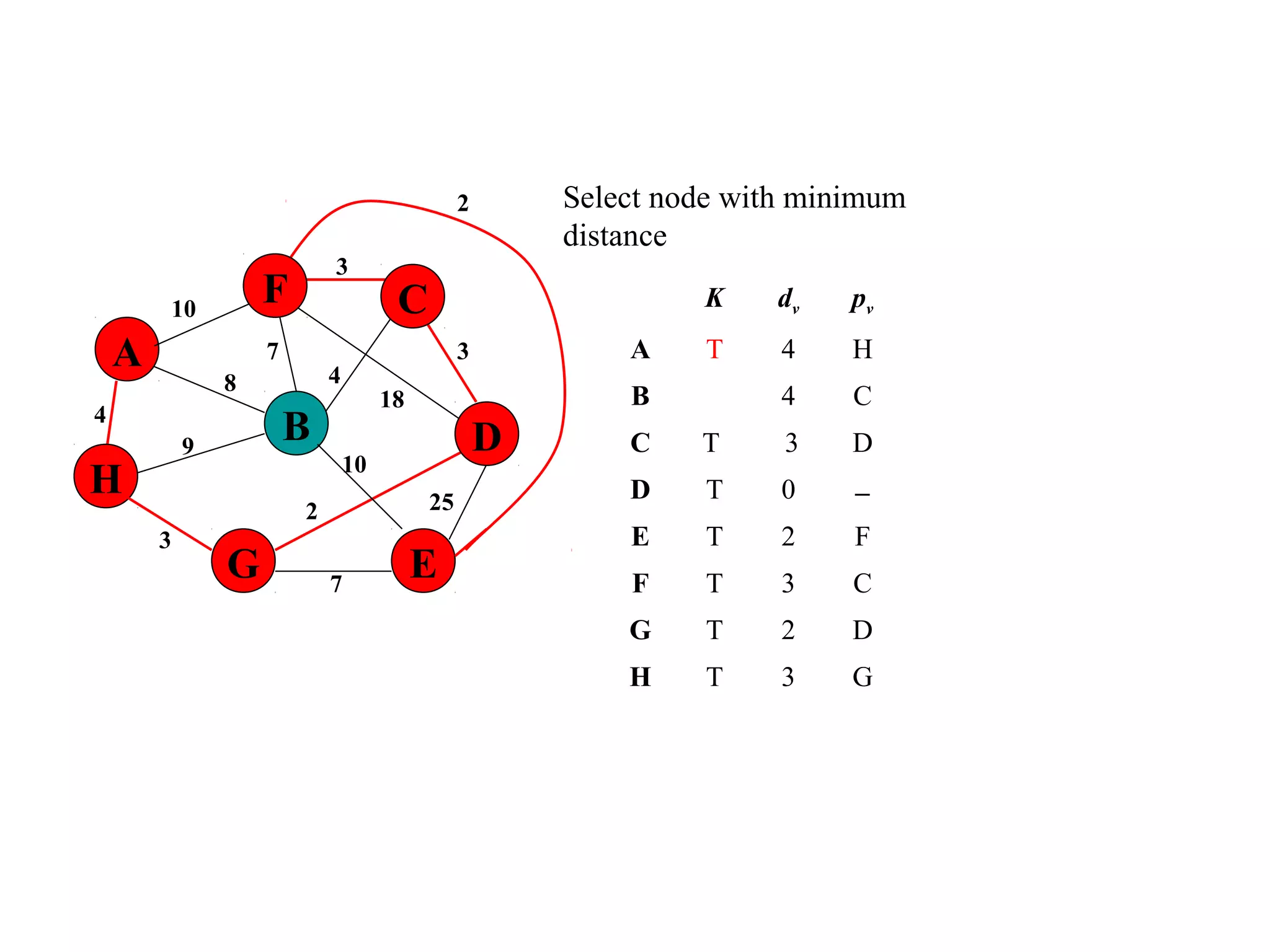
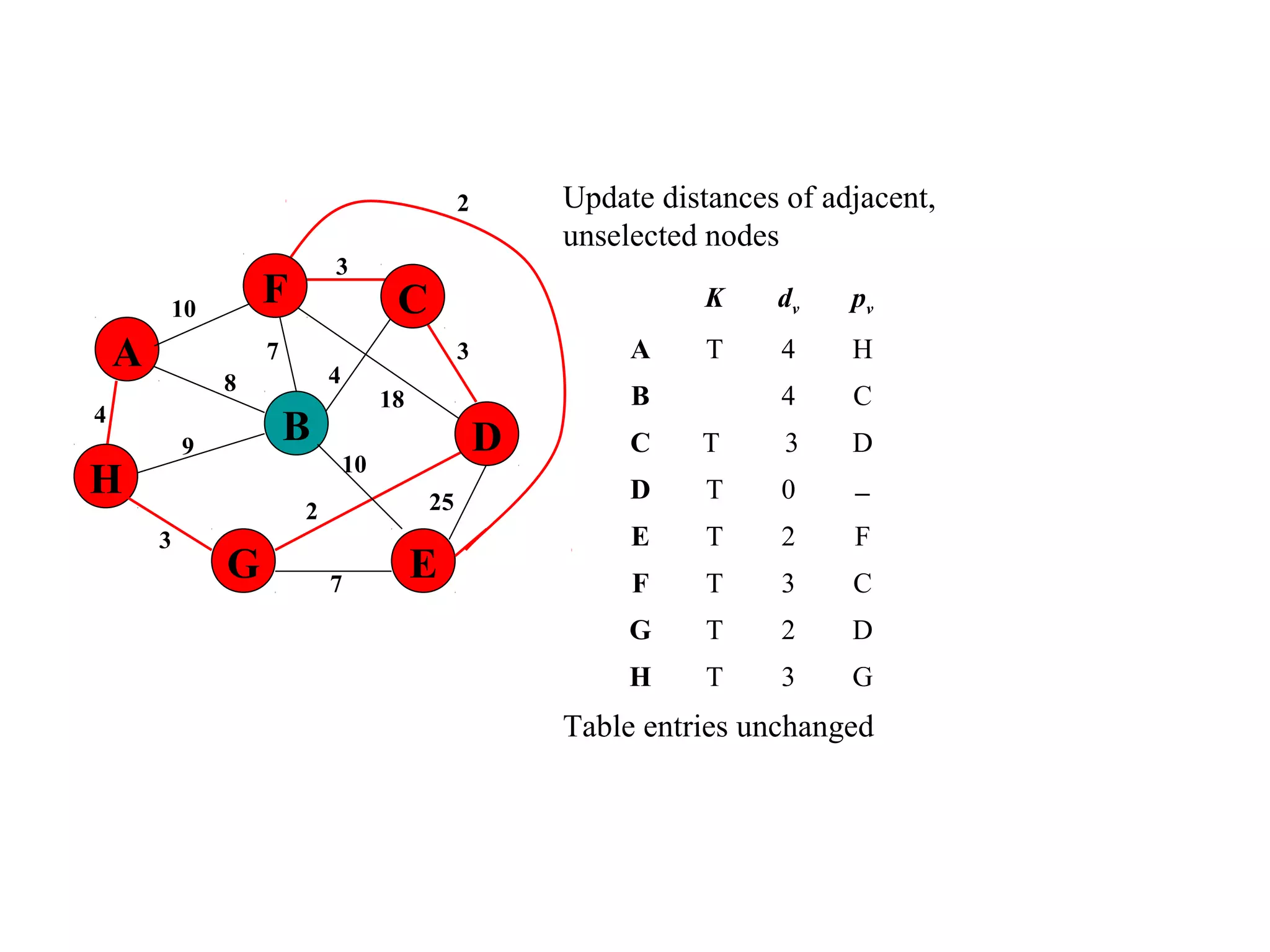
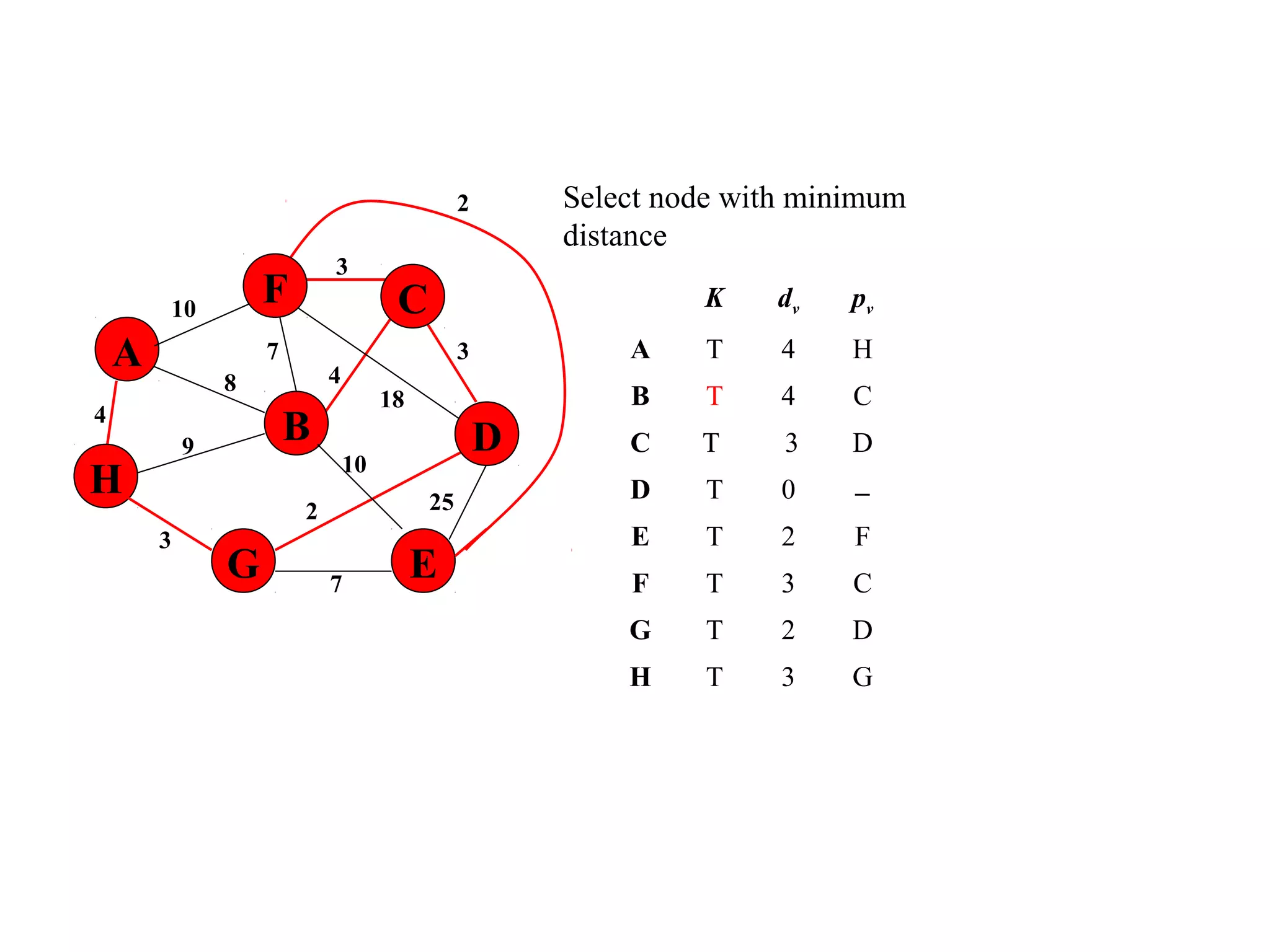
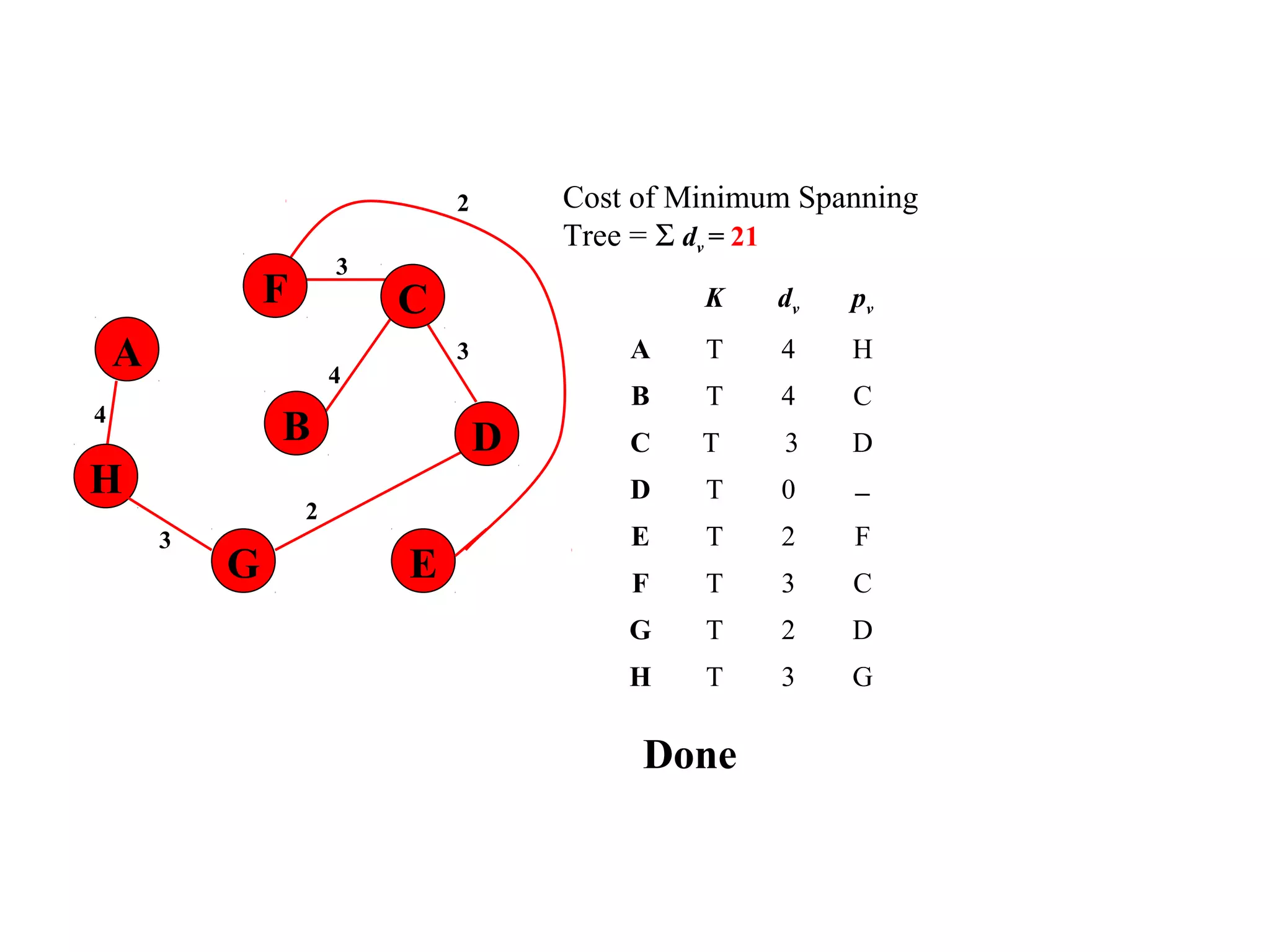
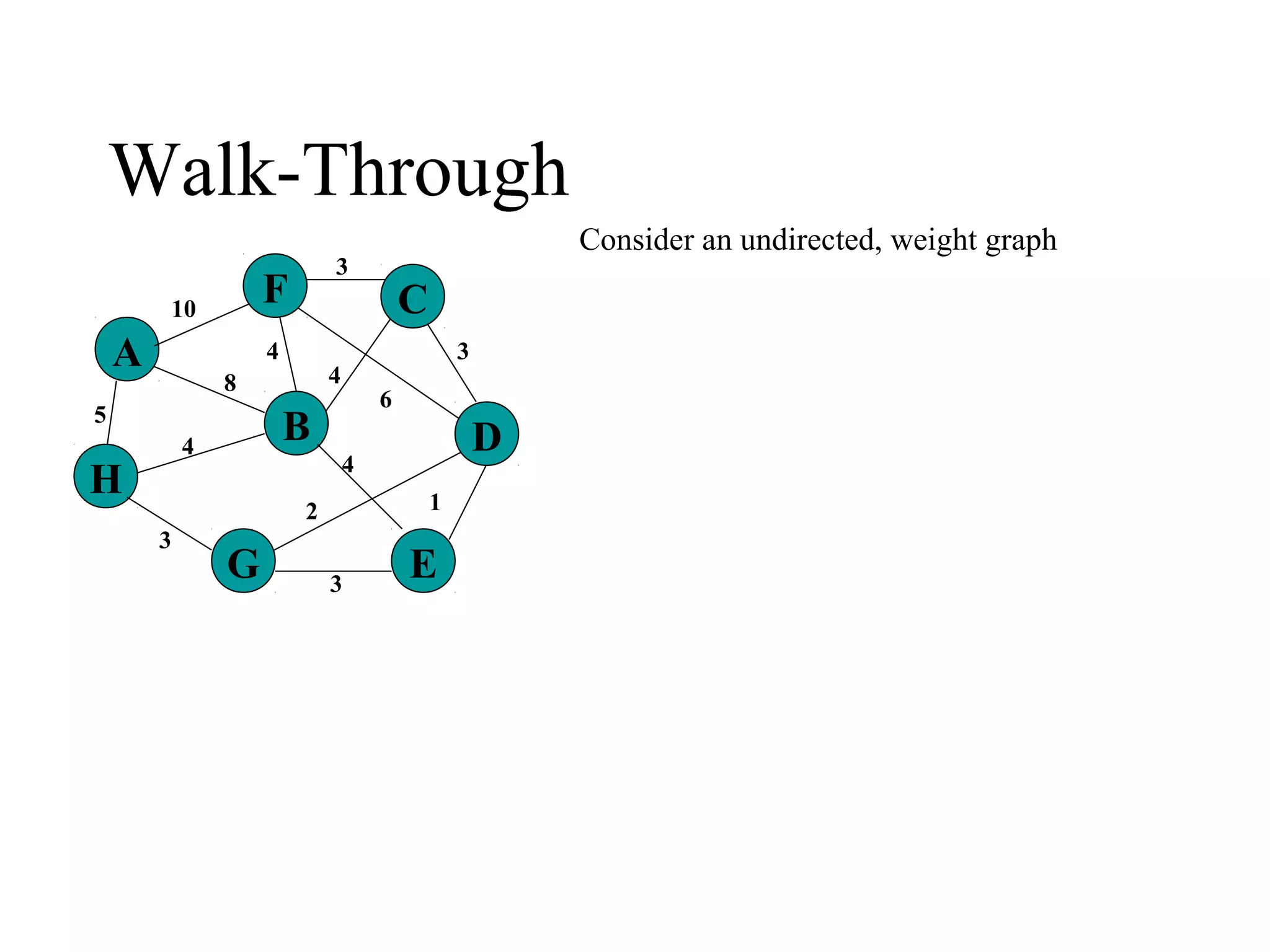
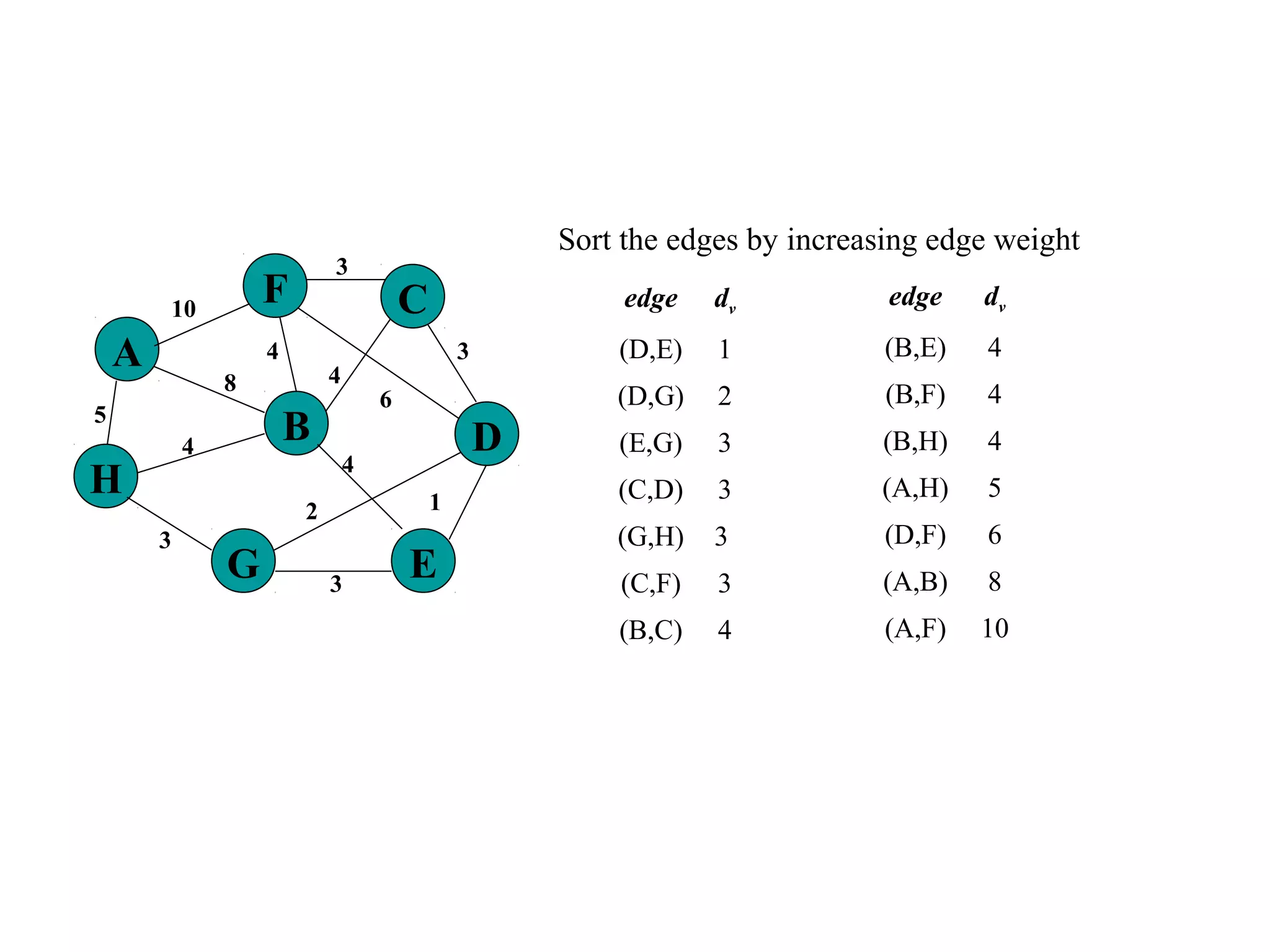
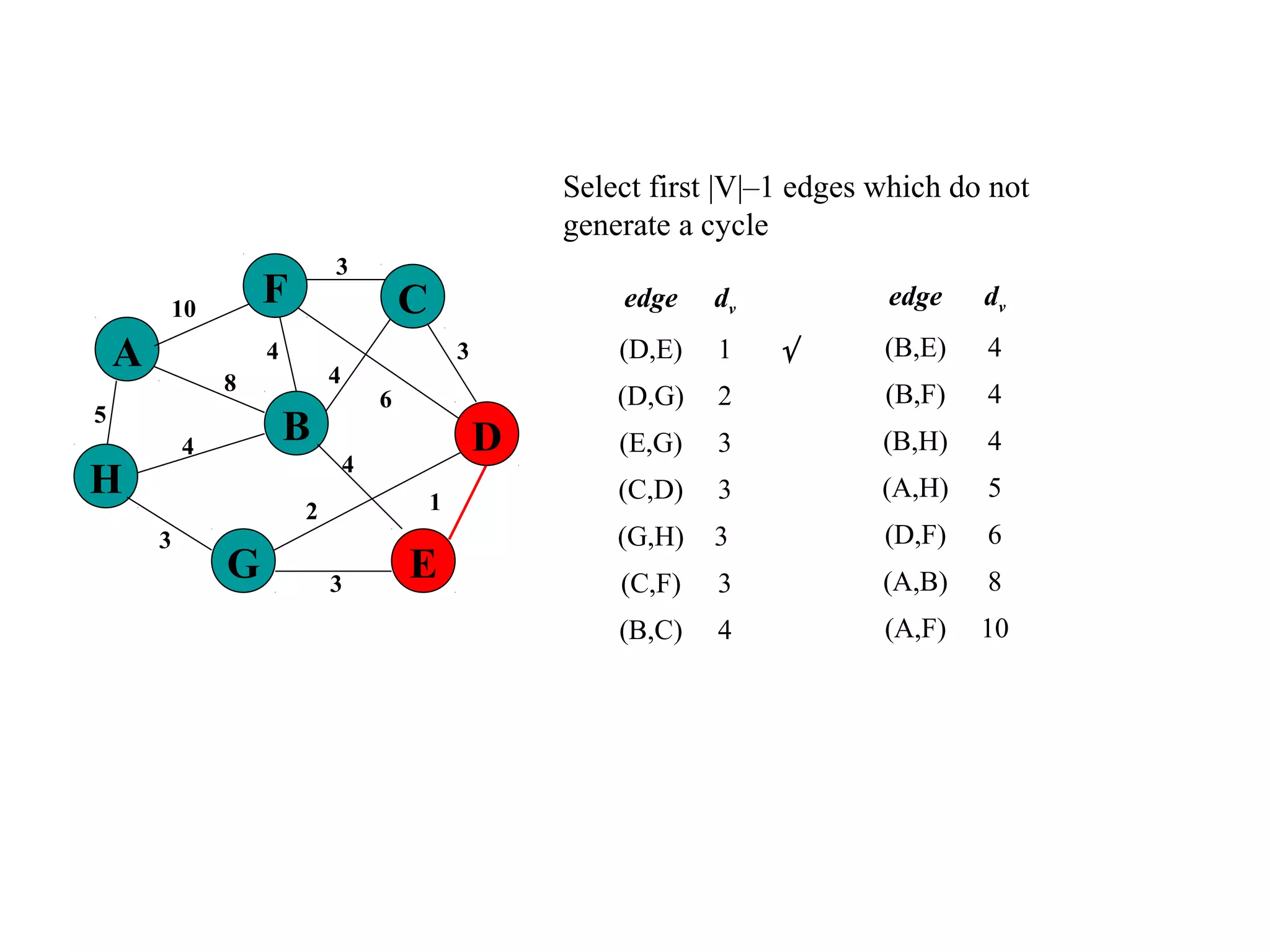
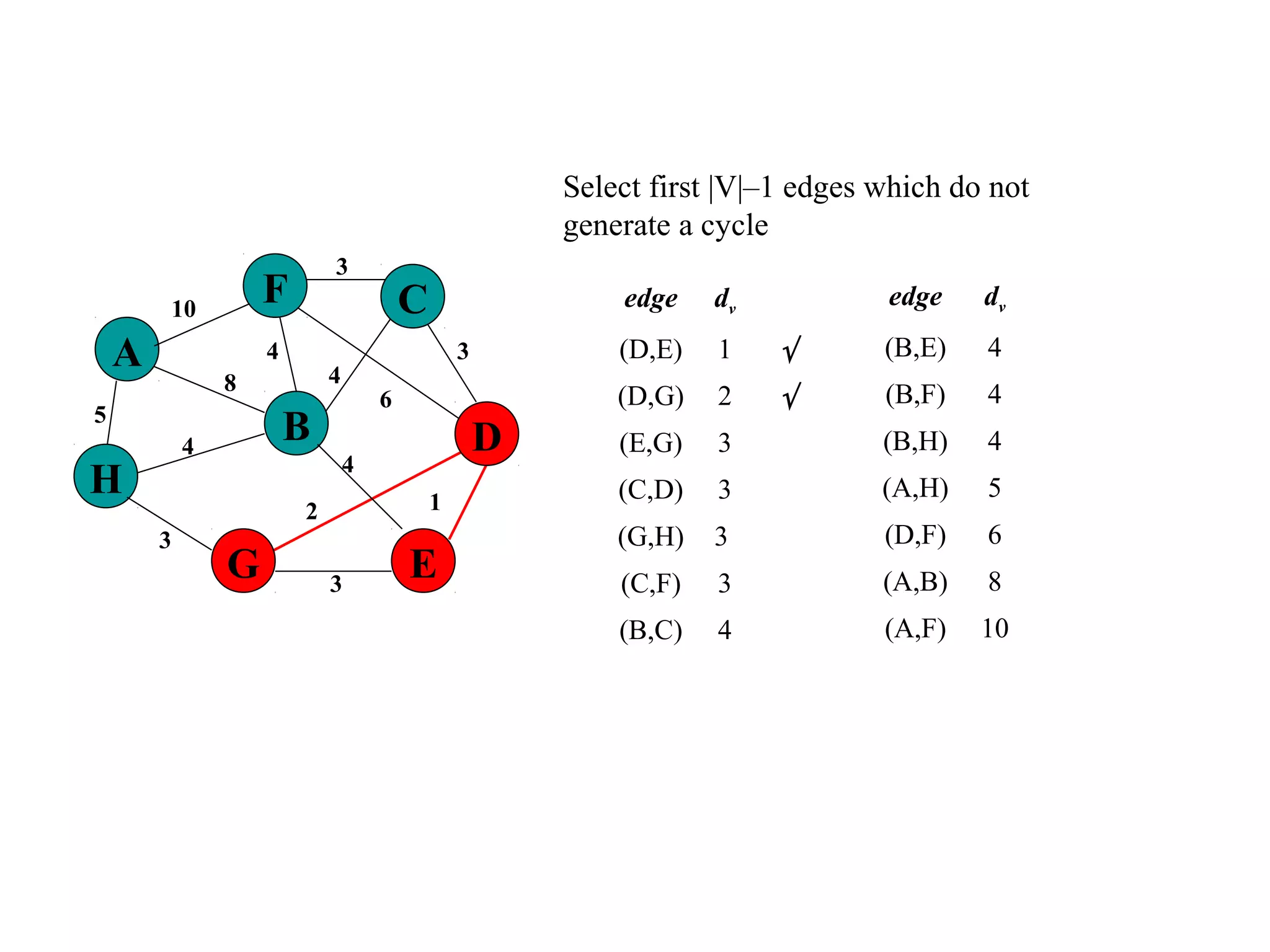
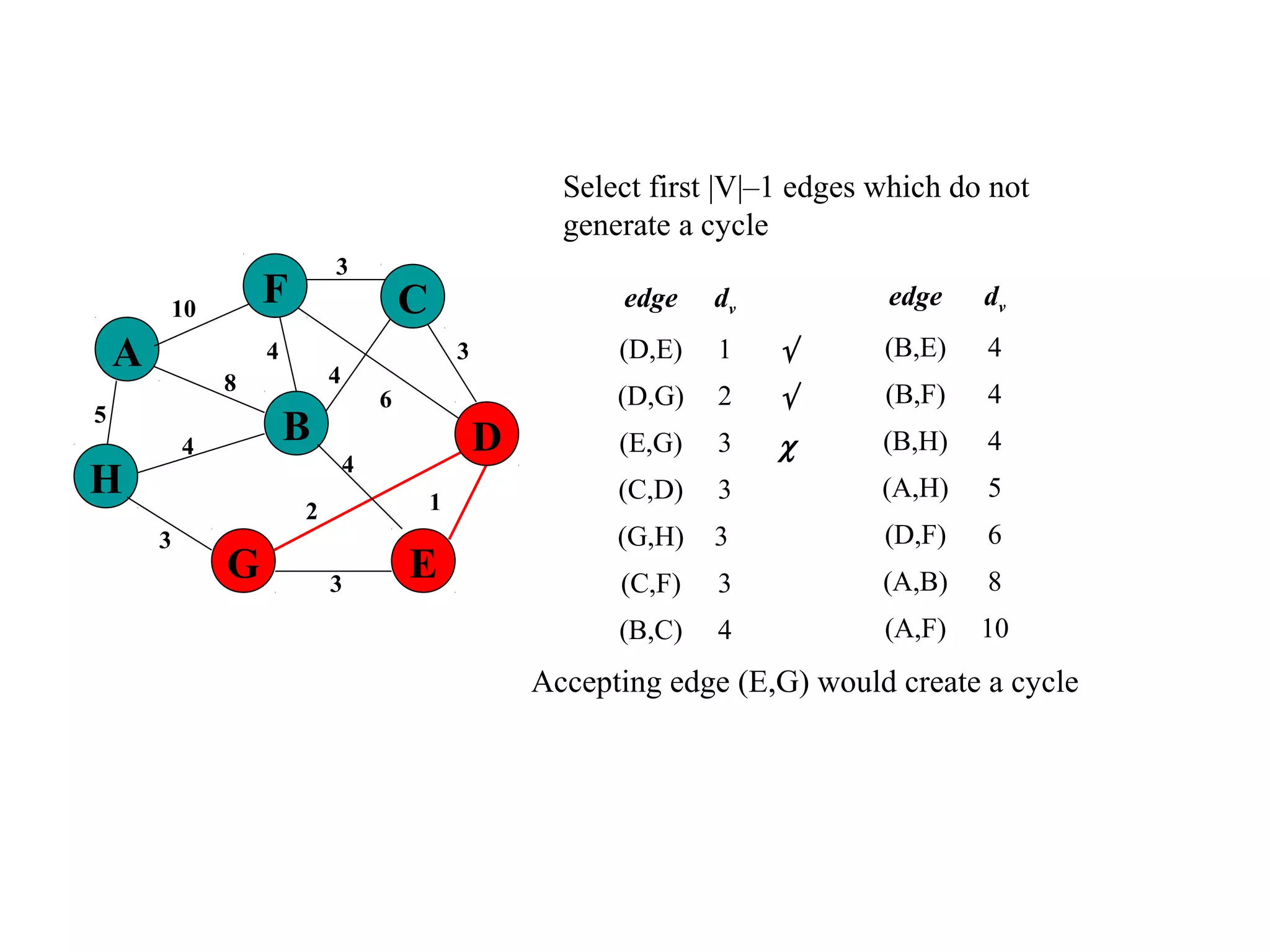
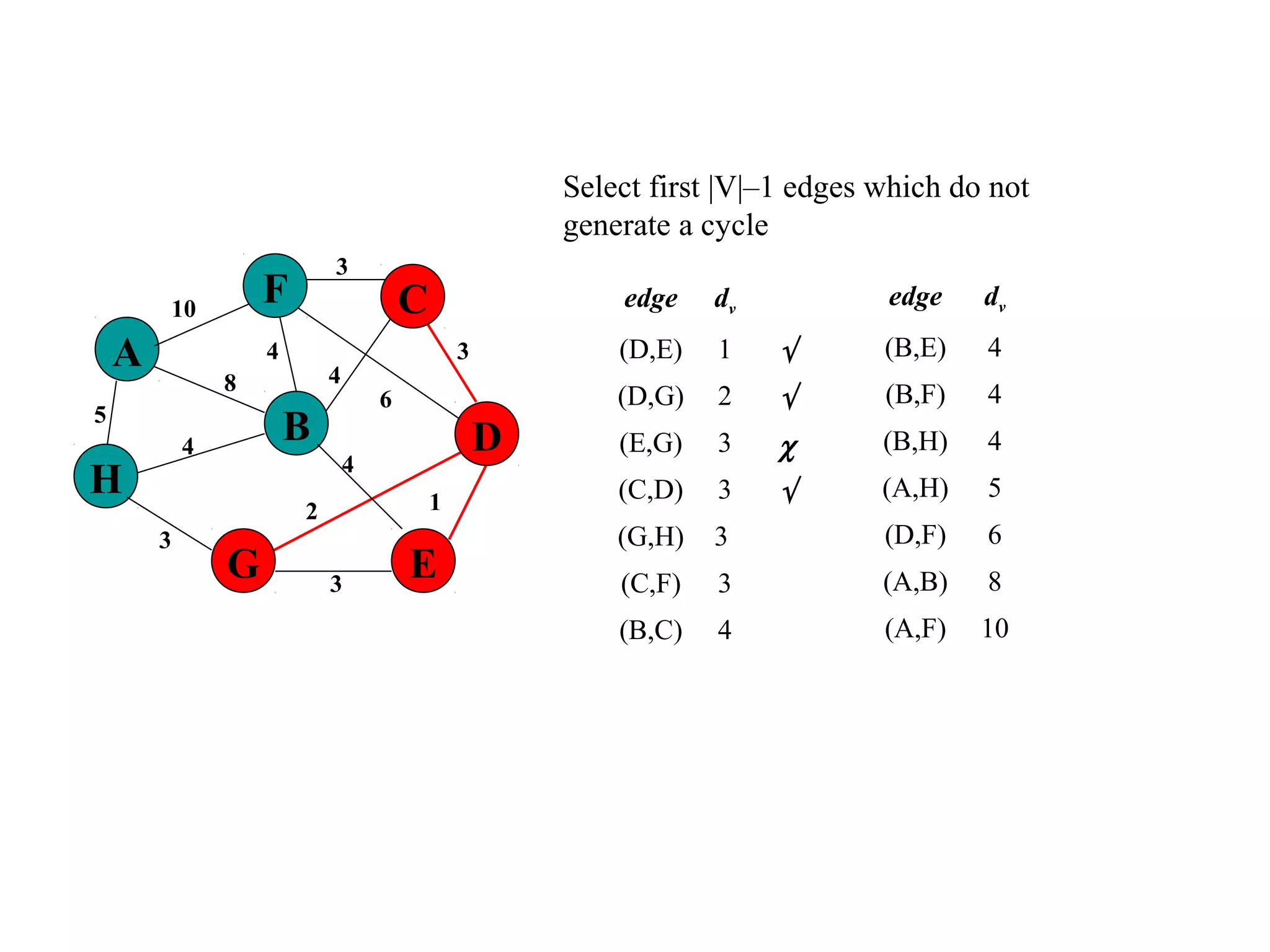
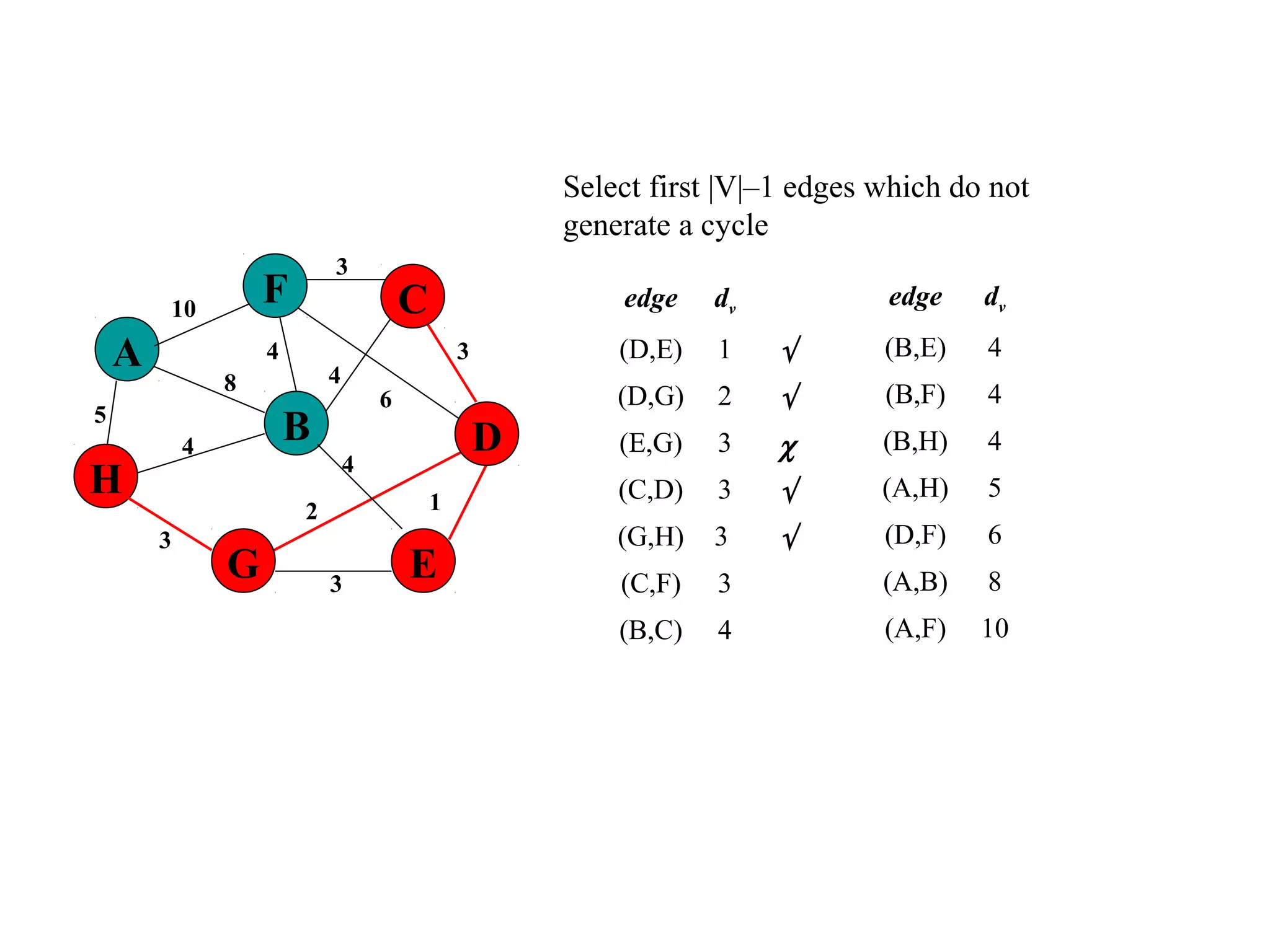
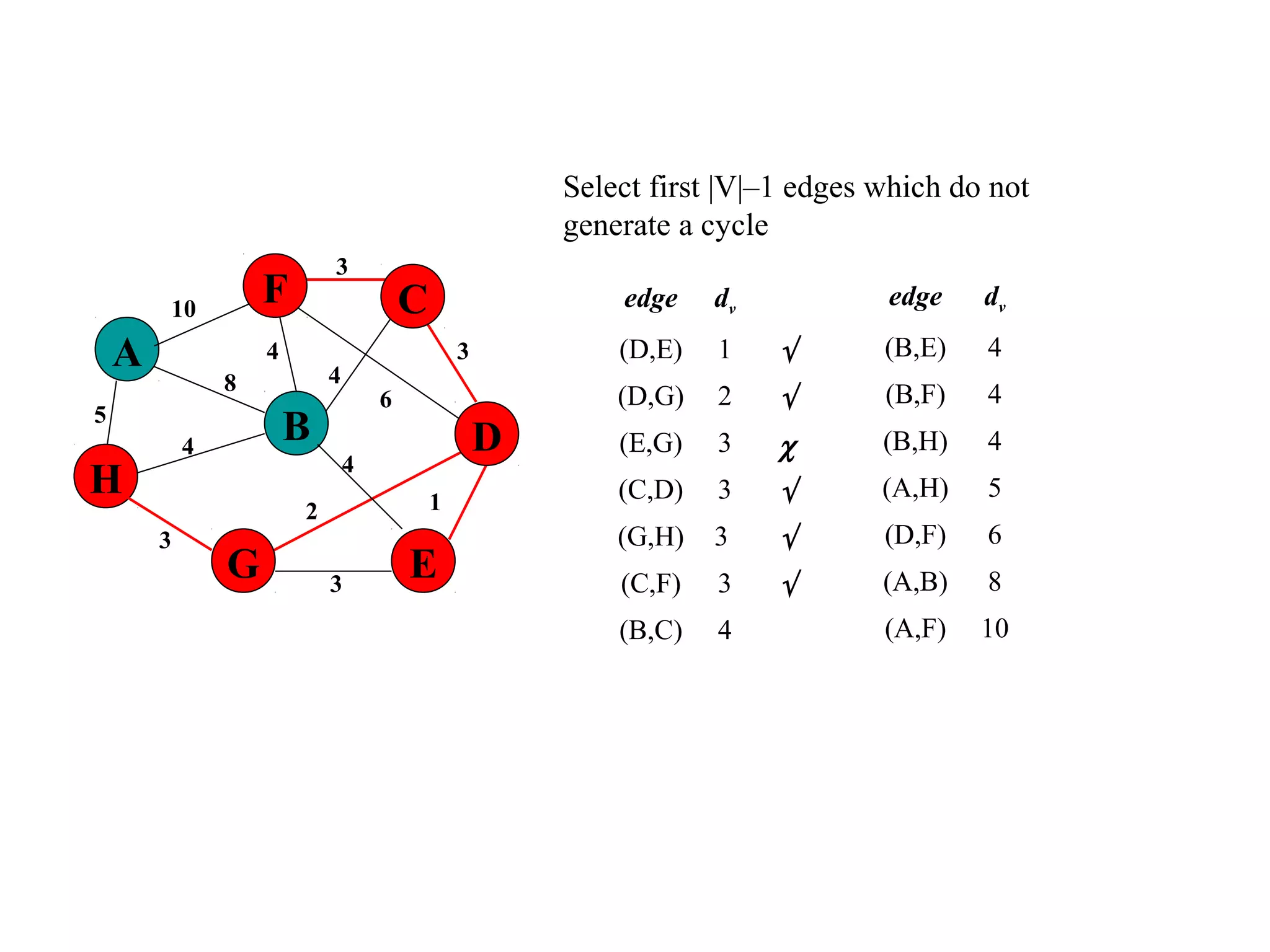
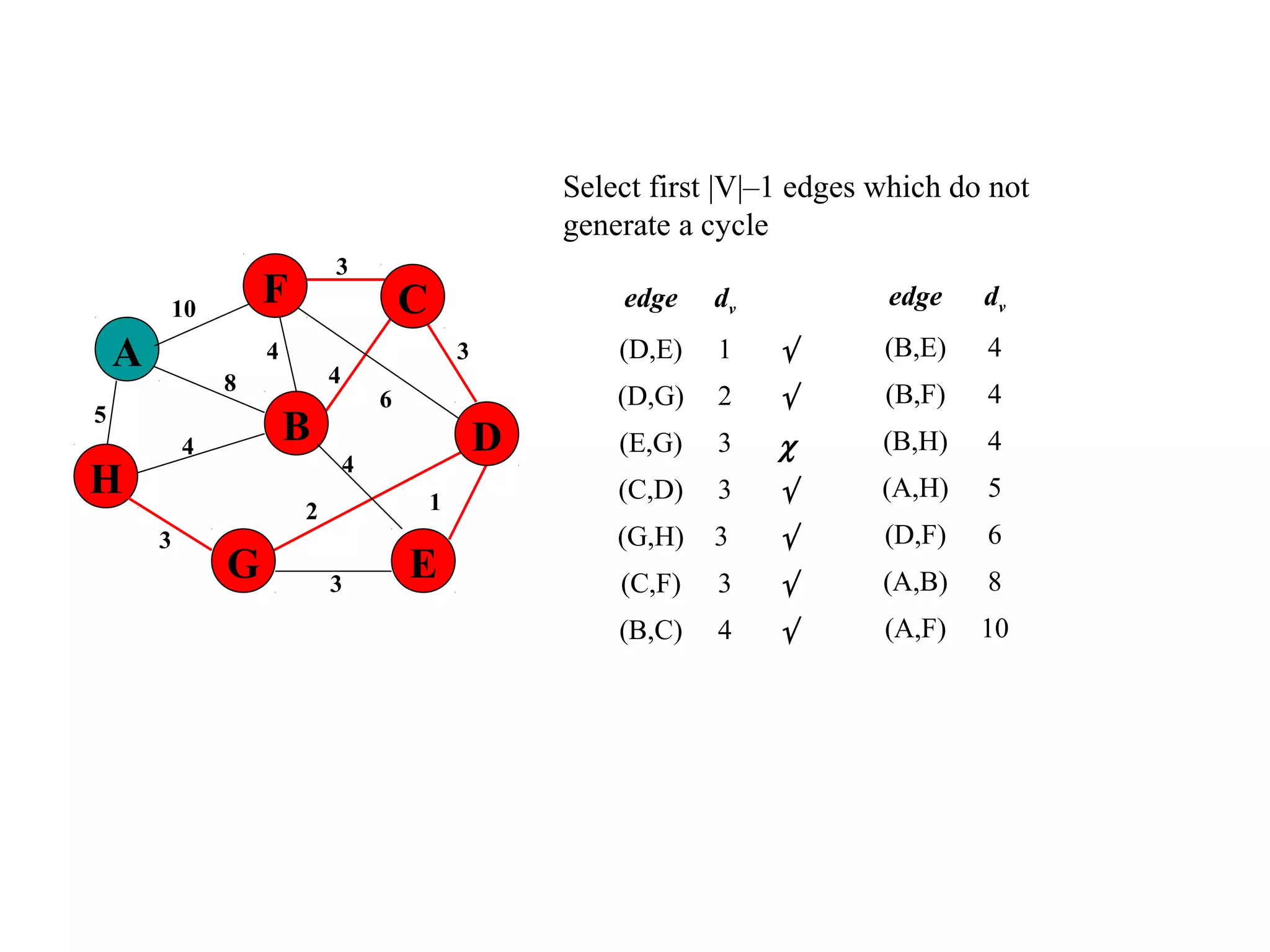
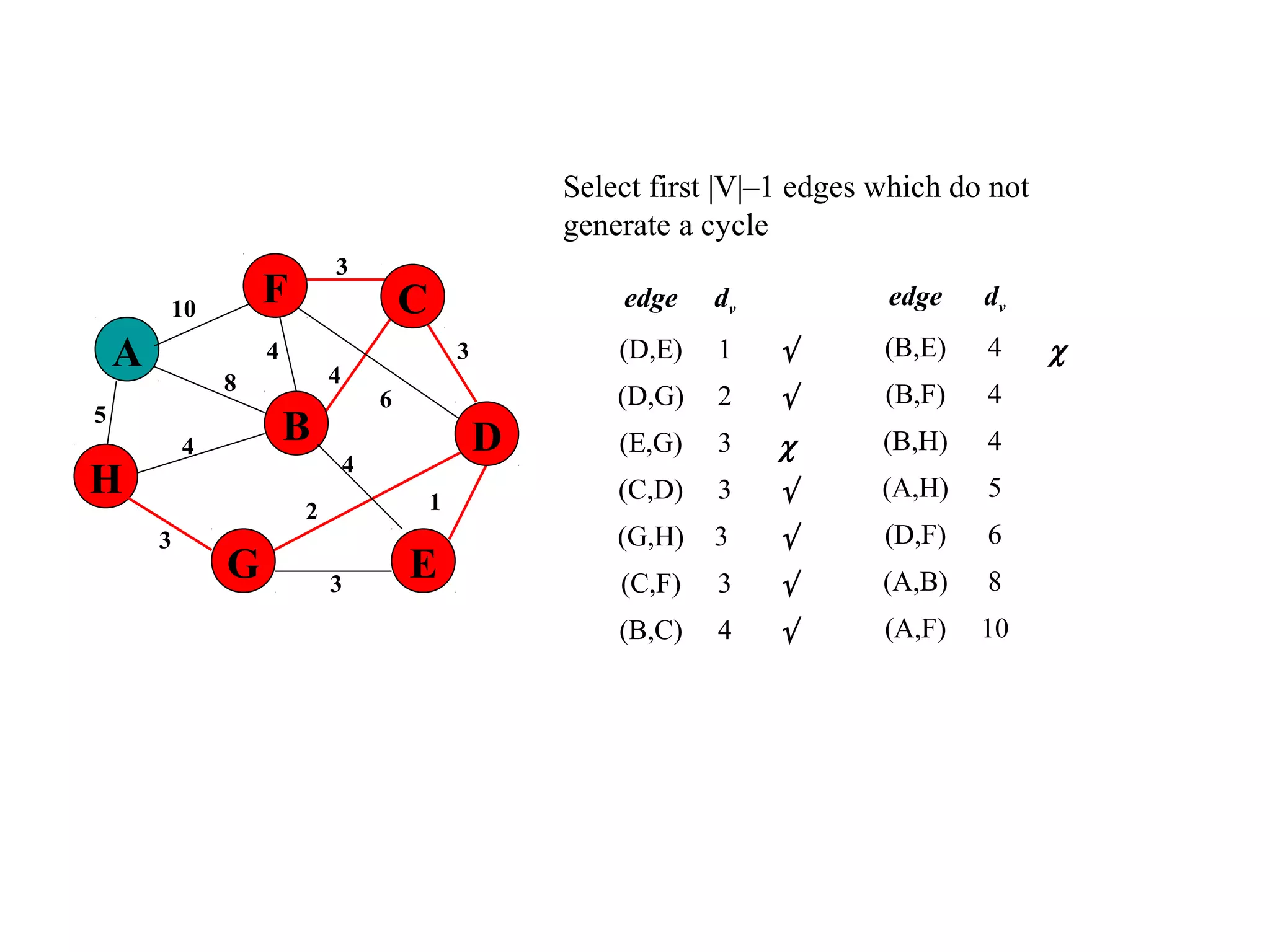
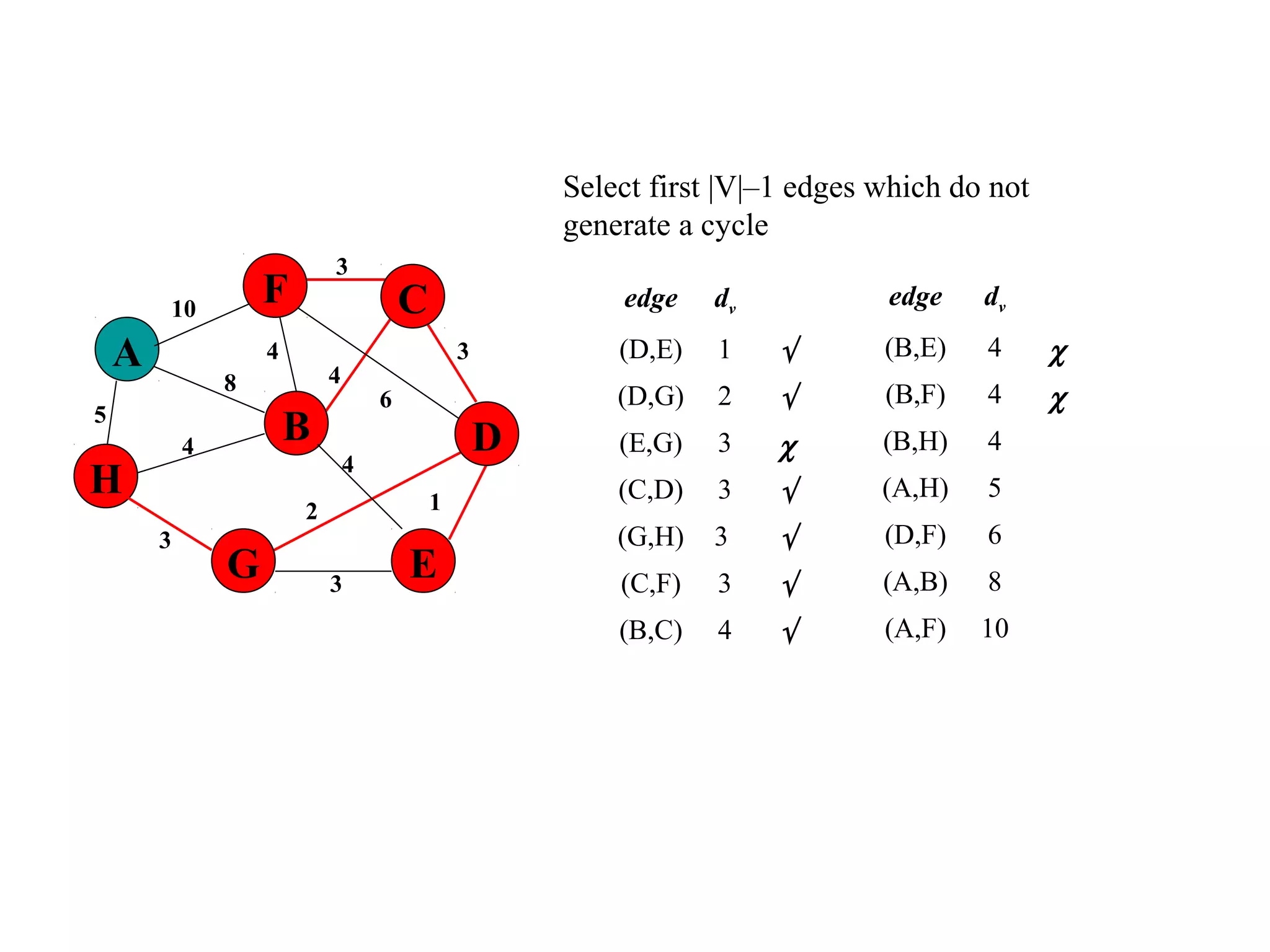
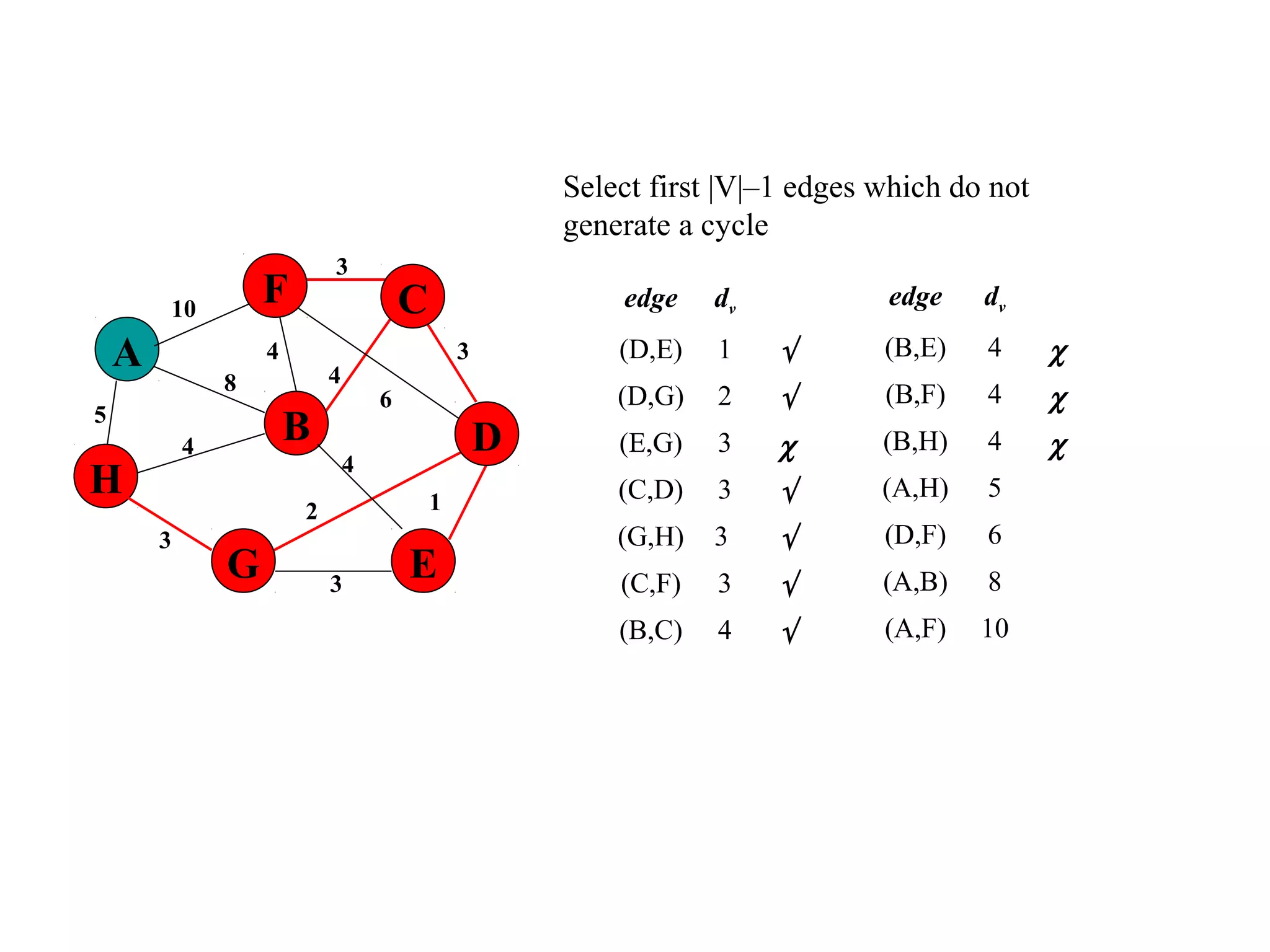
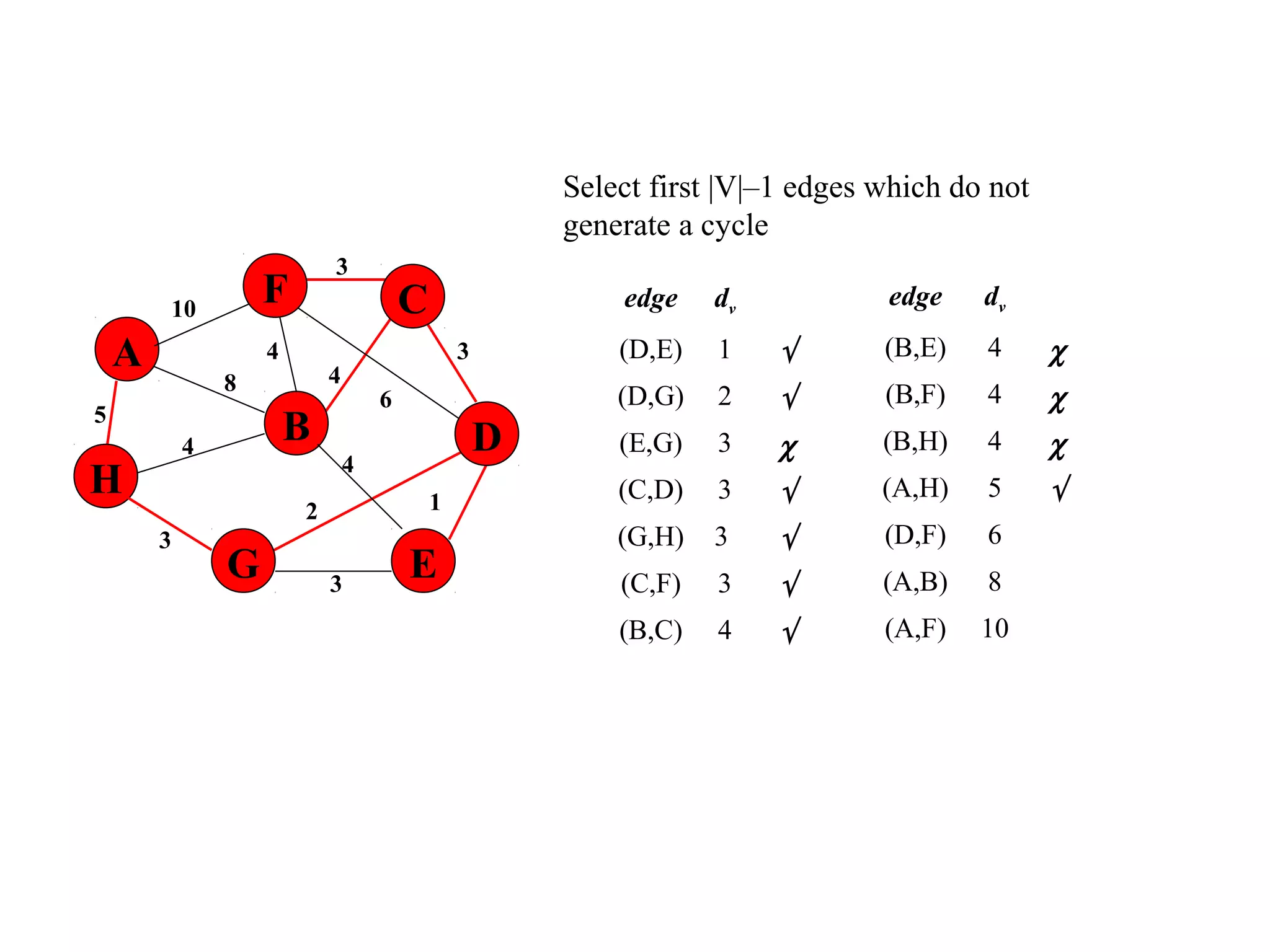
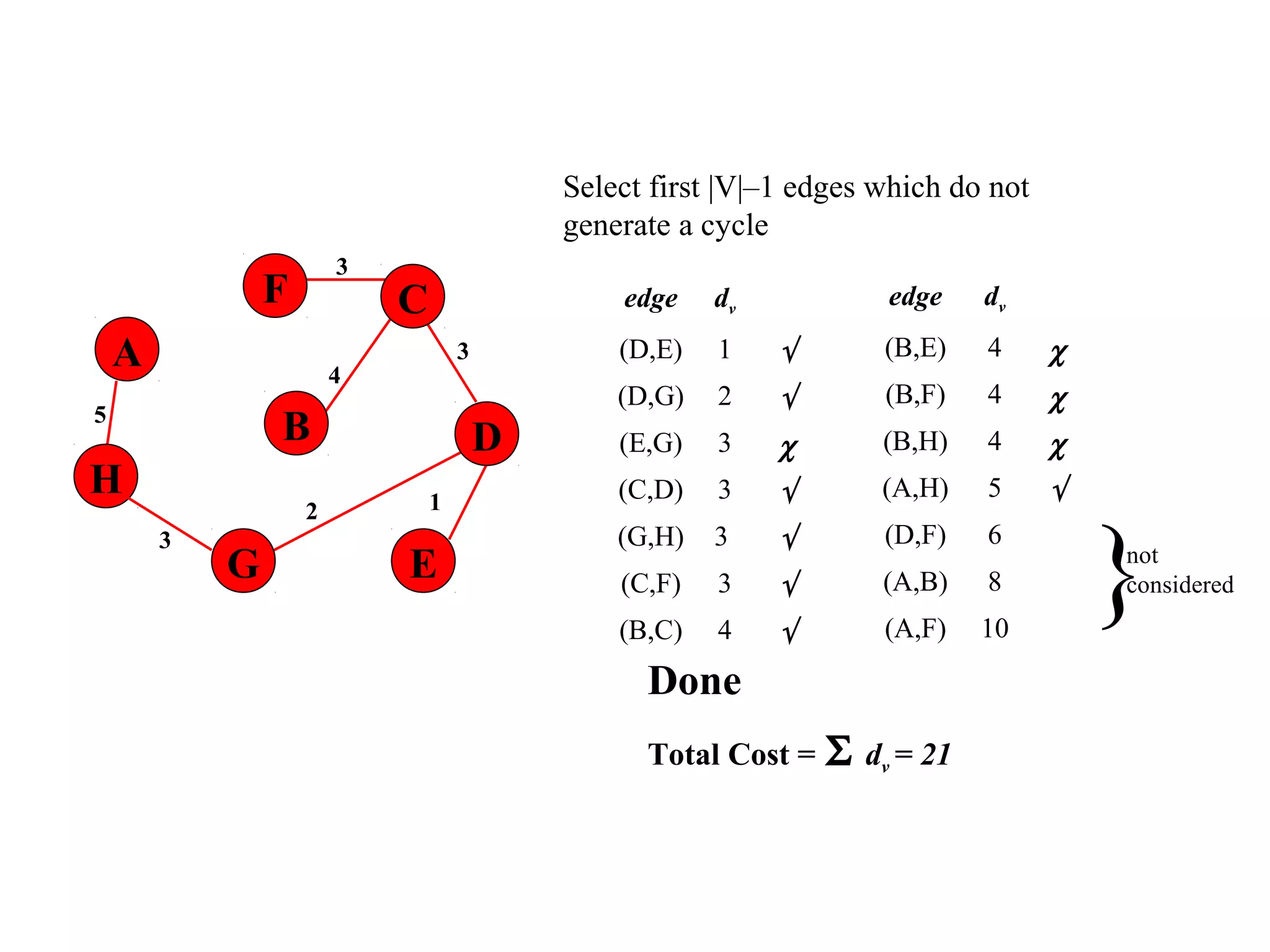
This document provides an introduction to graphs and graph terminology. It defines what a graph is composed of, including vertices and edges. It gives examples of graphs and has the student practice identifying vertices and edges. It also introduces common graph terminology like degree of a vertex, adjacent vertices, paths, circuits, bridges, Euler paths, and Euler circuits. Fleury's algorithm for finding an Euler circuit or path in a graph is described. The document uses examples and exercises to help students learn and practice applying these graph concepts.

1. UNIT-4
Graphs and
Graph Terminology

2. Graphs consist of
 points called vertices
 lines called edges
1. Edges connect two
vertices.
2. Edges only intersect
at vertices.
3. Edges joining a
vertex to itself are
called loops.
ExampleExample 1: The following picture1: The following picture
is a graph. List its vertices andis a graph. List its vertices and
edges.edges.
AA
B
CC
D
E

3. Example 2:
FlexoFlexo BenderBender LeelaLeela
FryFry AmyAmy
This is also a graph. The vertices just happen to have
people’s names.
Such a graph could represent friendships (or any kind of
relationship).
QuickTime™ and a
TIFF (LZW) decompressor
are needed to see this picture.
QuickTime™ and a
TIFF (LZW) decompressor
are needed to see this picture.
FarnsworthFarnsworth
ZoidbergZoidberg

4. FlexoFlexo
BenderBender
LeelaLeela FryFry
AmyAmy
FarnsworthFarnsworth
Now check out the graph below.
What can we say about it in comparison to the previous
figure?
QuickTime™ and a
TIFF (LZW) decompressor
are needed to see this picture.
QuickTime™ and a
TIFF (LZW) decompressor
are needed to see this picture.
ZoidbergZoidberg

5. • One graph may be drawn in (infinitely)
many ways, but it always provides us
with the same information.
• Graphs are a structure for describing
relationships between objects.
(The vertices denote the objects and the
edges represent the relationship.)
Moral of the Story

6. Graph TerminologyGraph Terminology

7. Graph TerminologyGraph Terminology
(ie - all the math-y jargon one could ask for)
 Adjacent Vertices are two vertices
that are joined by an edge.
 Adjacent Edges are two edges that
intersect at a vertex.
 The degree of a vertex is the
number of edges at that vertex.

8. Graph TerminologyGraph Terminology
A loop counts twice toward the
degree.
An odd vertex is a vertex of
odd degree.
An even vertex is a vertex of
even degree.

9. ExampleExample 3:3:
AA
BB
CC
DD
EE
1)1) Find the degree ofFind the degree of
each vertex.each vertex.
2)2) Is A adjacent to B?Is A adjacent to B?
Is D adjacent to A?Is D adjacent to A?
Is E adjacent toIs E adjacent to
itself?itself?
Is C adjacent toIs C adjacent to
itself?itself?
3)3) Is AB adjacent toIs AB adjacent to
BC?BC?
Is CE adjacent toIs CE adjacent to
BD?BD?

10. Graph TerminologyGraph Terminology
A path is a sequence of vertices
such that each vertex is adjacent to
the next. In a path, each edge can
be traveled only once.
•The length of a path is the number
of edges in that path.

11. Graph TerminologyGraph Terminology
•A path that starts and ends at
the same vertex is called a circuit.
•A graph is connected if any two
vertices can be joined by a path. If
this is not possible then the graph
is disconnected.

12. Graph TerminologyGraph Terminology
•The connected parts of a
disconnected graph are called
components.
•A bridge is an edge in a
connected graph whose
removal makes it disconnected.

13. B
H
S J
W
K
Example 4:
1) Find a path from B to K
passing through W but
not S.
2) Find a path from H to J
of length 4.
3) Find a circuit of length
5.
4) Find a circuit of length
1.
5) Find a bridge.Example 5: Draw a picture of a graph that satisfies the
following:
Vertices: A, B, C, D
Edges: AB, AC, AD, B is adjacent to D.

14. Graph TerminologyGraph Terminology
•An Euler Path is a path that
travels through every edge of the
graph (once and only once).
•An Euler Circuit is a circuit that
travels through every edge of a
graph.

15. R
A
L
D
R
A
L
D
ExampleExample 6:6: The graph on the left has no Euler
paths, but the one on the right has several.

16. §5.4 - 5.5 Graph Models and
Euler’s Theorems
“Now I will have less
distraction.”
- Leonhard Euler
after losing sight
in his right eye.

17. Königsberg’s Bridges II
(The rare sequel that is not entirely gratuitous.)
Recall from Tuesday the
puzzle that the
residents of Königsburg
had been unable to
solve until Euler’s
arrival:
• Is there a way to cross
all seven bridges
exactly once and return
to your starting point?
• Is there even a way to
cross all seven bridges
exactly once?
A
A stylized (i.e. - inaccurate)
map of Königsberg’s Bridges.
A
R
L
D

18. A
R
A
L
D
R
A
L
D
What Euler realized was that most of the information
on the maps had no impact on the answers to the two
questions.
By thinking of each bank and island as a vertex and each
bridge as an edge joining them Euler was able to model
the situation using the graph on the right. Hence, the
Königsberg puzzle is the same as asking if the graph has
an Euler path or Euler circuit.

19. Example: Slay-ageSlay-age• The Scooby Gang needs to patrol the following section of
town starting at Sunnydale High (labeled G). Draw a graph
that models this situation, assuming that each side of the
street must be checked except for those along the park.
(Map is from p. 206)

20. Example 2: (Exercise 21, pg 207) The
map to the right of downtown Kingsburg,
shows the Kings River running through
the downtown area and the three islands
(A, B, and C) connected to each other
and both banks by seven bridges. The
Chamber of Commerce wants to design a
walking tour that crosses all the bridges.
Draw a graph that models the layout of
Kingsburg.

21. Example 3:
The Kevin Bacon Game
(http://www.cs.virginia.edu/oracle/)

22. Euler’s Theorems
• Euler’s Theorem 1Euler’s Theorem 1
(a) If a graph has any odd vertices, then
it cannot have an Euler circuit.
(b) If a graph is connected and every
vertex is even, then it has at least one
Euler circuit.

23. • Euler’s Theorem 2Euler’s Theorem 2
(a) If a graph has more than two odd
vertices, then it cannot have an Euler
path.
(b) If a connected graph has exactly
two odd vertices then it has at least one
Euler path starting at one odd vertex
and ending at another odd vertex.

24. Example 4: Königsburg’s Bridges IIIKönigsburg’s Bridges III (The Search For More MoneyThe Search For More Money)
Let us consider again the Königsburg Brdige puzzle as represented by the graph
below:
R
A
L
D
We have already seen that the puzzle boils down to whether this graph has
an Euler path and/or an Euler circuit. Does this graph have either?

25. Example 5: (Exercise 60, pg 214) Refer to Example 2. Is it possible to take a
walk such that you cross each bridge exactly once? Explain why or why not.
N
A B C
S

26. ExampleExample 6: Unicursal Tracings6: Unicursal Tracings
Recall the routing problems presented on Tuesday:
•“Do these drawings have unicursal tracings? If so, are they open or closed?”
(a) (b)
(c)
How might we answer these queries? Well, if we add vertices to the corners of the
tracings we can reduce the questions to asking whether the following graphs have Euler
paths (open tracing) and/or Euler circuits (closed tracing).

27. • Euler’s Theorem 3Euler’s Theorem 3
(a) The sum of the degrees of all the
vertices of a graph equals twice the
number of edges.
(b) A graph always has an even
number of odd vertices.

28. A quick summary . . .A quick summary . . .
Number of odd verticesNumber of odd vertices ConclusionConclusion
0 Graph has Euler
circuit(s)
2 Graph has Euler
path(s) but no Euler
circuit
4, 6, 8, . . . Graph has no Euler
path and no Euler
circuit
1, 3, 5, . . . Impossible!

29. §5.6 Fleury’s Algorithm

30. • Euler’s Theorems give us a simple way
to see whether an Euler circuit or an
Euler path exists in a given graph, but
how do we find the actual circuit or
path?
• We could use a “guess-and-check”
method, but for a large graph this could
lead to many wasted hours--and not
wasted in a particularly fun way!

31. Algorithms
An algorithm is a set of procedures/rules that, when
followed, will always lead to a solution* to a
given problem.
• Some algorithms are formula driven--they arrive
at answers by taking data and ‘plugging-in’ to
some equation or function.
• Other algorithms are directive driven--they arrive
at answers by following a given set of directions.

32. Fleury’s Algorithm
• The Idea:
“Don’t burn your bridges behind you.”
(“bridges”: graph-theory bridges, not real world)
• When trying to find an Euler path or an Euler
circuit, bridges are the last edges we should
travel.
• Subtle point: Once we have traversed an
edge we no longer care about it--so by
“bridges” we mean the bridges of the part of
the graph that we haven’t traveled yet.

33. ExampleExample 1:1: Does this graph have an Euler circuit? If so, find
one.
A
B
C
D
E
F

34. Fleury’sFleury’s AlgorithmAlgorithm
1) Ensure the graph is connected and all the
vertices are even*.
2) Pick any vertex as the starting point.
3) When you have a choice, always travel
along an edge that is not a bridge of the yet-
to-be-traveled part of the graph.
4) Label the edges in the order which you
travel.
5) When you can’t travel anymore, stop.
* - This works when we have an Euler circuit. If we only
have a path, we must start at one of (two) the odd vertices.

35. ExampleExample 2:2: Do the following drawings have unicursal tracings? If so,
label the edges 1, 2, 3, . . . In the order in which they can be traced.

36. Example 3: (Exercise 60, pg 214) The
map to the right of downtown Kingsburg,
shows the Kings River running through
the downtown area and the three islands
(A, B, and C) connected to each other
and both banks by seven bridges. The
Chamber of Commerce wants to design a
walking tour that crosses all the bridges.
Draw a graph that models the layout of
Kingsburg.
It was shown yesterday that it was
possible to take a walk in such that you
cross each bridge exactly once. Show
how.
N
A B C
S

37. Example: Slay-ageSlay-age• The Scooby Gang needs to patrol the following section of
town starting at Sunnydale High (labeled G). Suppose that
they must check each side of the street except for those
along the park. Find an optimal route for our intrepid demon
hunters to take.

38. North Bank (N)
A
B
C
South Bank (S)
Quiz 1, problem 2

39. Mathematics and the Arts?
• One of Euler’s 800+One of Euler’s 800+
publicationspublications
included a treatiseincluded a treatise
on music theory.on music theory.
• Book was too math-Book was too math-
y for mosty for most
composers--toocomposers--too
music-y for mostmusic-y for most
mathematiciansmathematicians

40. Mathematics and the Arts?
• While Euler’sWhile Euler’s
theories did nottheories did not
catch on, acatch on, a
relationship betweenrelationship between
mathematics andmathematics and
music compositionmusic composition
does exist in what isdoes exist in what is
called thecalled the goldengolden
ratioratio..

41. Fibonacci Numbers
• The Fibonacci Numbers are
those that comprise the
sequence:
1, 1, 2, 3, 5, 8, 13, 21, . . .
• The sequence can be
defined by:
F1=1, F2=1;
Fn=Fn-1+Fn-2
• These numbers can be used
to draw a series of ‘golden’
rectangles like those to the
right.

42. Fibonacci Numbers
• The sequence of
Fibonacci Ratios -
fractions like 3/5, 5/8,
8/13 approach a
number called the
Golden Ratio
(≈0.61803398…)

43. The Golden Ratio
• Several of Mozart’s piano
sonatas make use of this
ratio.
• At the time such pieces
regularly employed a
division into two parts
1. Exposition and
Development
2. Recapitulation
• In Piano Sonata No. 1 the
change between parts
occurs at measure 38 of
100. (which means that part
2 is 62 ≈ 0.618 x 100)

44. The Golden Ratio
• Another example in music is
in the ‘Hallelujah’ chorus in
Handel’s Messiah.
• The piece is 94 measures
long.
• Important events in piece:
1. Entrance of trumpets -
“King of Kings” occurs in
measures 57-58 ≈ (8/13) x
94
2. “The kingdom of glory…”
occurs in meas.
34-35 ≈ (8/13) x 57
etc, etc. . .

45. The Golden Ratio in Art
H
Approx. = 0.618 x H

46. The Golden Ratio in Art
H
Approx. = 0.618 x H

47. The Golden Ratio in Art

48. The Golden Ratio in Art
.618xHt.
0.618 x Width

49. The Golden Ratio in Art
.618xHt.
0.618 x Width

50. Minimum Spanning Trees
Prim’s Algorithm
Kruskal’s Algorithm

51. Definition
• A Minimum Spanning Tree (MST) is a
subgraph of an undirected graph such that
the subgraph spans (includes) all nodes, is
connected, is acyclic, and has minimum
total edge weight

52. Algorithm Characteristics
• Both Prim’s and Kruskal’s Algorithms work
with undirected graphs
• Both work with weighted and unweighted
graphs but are more interesting when edges
are weighted
• Both are greedy algorithms that produce
optimal solutions

53. Prim’s Algorithm
• Similar to Dijkstra’s Algorithm except that
dv records edge weights, not path lengths

54. Walk-Through
Initialize array
K dv pv
A F ∞ −
B F ∞ −
C F ∞ −
D F ∞ −
E F ∞ −
F F ∞ −
G F ∞ −
H F ∞ −
4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
2

55. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Start with any node, say D
K dv pv
A
B
C
D T 0 −
E
F
G
H
2

56. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Update distances of adjacent,
unselected nodes
K dv pv
A
B
C 3 D
D T 0 −
E 25 D
F 18 D
G 2 D
H
2

57. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Select node with minimum
distance
K dv pv
A
B
C 3 D
D T 0 −
E 25 D
F 18 D
G T 2 D
H
2

58. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Update distances of adjacent,
unselected nodes
K dv pv
A
B
C 3 D
D T 0 −
E 7 G
F 18 D
G T 2 D
H 3 G
2

59. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Select node with minimum
distance
K dv pv
A
B
C T 3 D
D T 0 −
E 7 G
F 18 D
G T 2 D
H 3 G
2

60. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Update distances of adjacent,
unselected nodes
K dv pv
A
B 4 C
C T 3 D
D T 0 −
E 7 G
F 3 C
G T 2 D
H 3 G
2

61. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Select node with minimum
distance
K dv pv
A
B 4 C
C T 3 D
D T 0 −
E 7 G
F T 3 C
G T 2 D
H 3 G
2

62. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Update distances of adjacent,
unselected nodes
K dv pv
A 10 F
B 4 C
C T 3 D
D T 0 −
E 2 F
F T 3 C
G T 2 D
H 3 G
2

63. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Select node with minimum
distance
K dv pv
A 10 F
B 4 C
C T 3 D
D T 0 −
E T 2 F
F T 3 C
G T 2 D
H 3 G
2

64. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Update distances of adjacent,
unselected nodes
K dv pv
A 10 F
B 4 C
C T 3 D
D T 0 −
E T 2 F
F T 3 C
G T 2 D
H 3 G
2
Table entries unchanged

65. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Select node with minimum
distance
K dv pv
A 10 F
B 4 C
C T 3 D
D T 0 −
E T 2 F
F T 3 C
G T 2 D
H T 3 G
2

66. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Update distances of adjacent,
unselected nodes
K dv pv
A 4 H
B 4 C
C T 3 D
D T 0 −
E T 2 F
F T 3 C
G T 2 D
H T 3 G
2

67. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Select node with minimum
distance
K dv pv
A T 4 H
B 4 C
C T 3 D
D T 0 −
E T 2 F
F T 3 C
G T 2 D
H T 3 G
2

68. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Update distances of adjacent,
unselected nodes
K dv pv
A T 4 H
B 4 C
C T 3 D
D T 0 −
E T 2 F
F T 3 C
G T 2 D
H T 3 G
2
Table entries unchanged

69. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Select node with minimum
distance
K dv pv
A T 4 H
B T 4 C
C T 3 D
D T 0 −
E T 2 F
F T 3 C
G T 2 D
H T 3 G
2

70. 4
A
H
B
F
E
D
C
G
2
3
4
3
3
Cost of Minimum Spanning
Tree = Σ dv = 21
K dv pv
A T 4 H
B T 4 C
C T 3 D
D T 0 −
E T 2 F
F T 3 C
G T 2 D
H T 3 G
2
Done

71. Kruskal’s Algorithm
Work with edges, rather than nodes
Two steps:
– Sort edges by increasing edge weight
– Select the first |V| – 1 edges that do not
generate a cycle

72. Walk-Through
Consider an undirected, weight graph
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10

73. Sort the edges by increasing edge weight
edge dv
(D,E) 1
(D,G) 2
(E,G) 3
(C,D) 3
(G,H) 3
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

74. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2
(E,G) 3
(C,D) 3
(G,H) 3
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

75. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2 √
(E,G) 3
(C,D) 3
(G,H) 3
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

76. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2 √
(E,G) 3 χ
(C,D) 3
(G,H) 3
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10
Accepting edge (E,G) would create a cycle

77. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2 √
(E,G) 3 χ
(C,D) 3 √
(G,H) 3
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

78. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2 √
(E,G) 3 χ
(C,D) 3 √
(G,H) 3 √
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

79. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2 √
(E,G) 3 χ
(C,D) 3 √
(G,H) 3 √
(C,F) 3 √
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

80. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2 √
(E,G) 3 χ
(C,D) 3 √
(G,H) 3 √
(C,F) 3 √
(B,C) 4 √
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

81. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2 √
(E,G) 3 χ
(C,D) 3 √
(G,H) 3 √
(C,F) 3 √
(B,C) 4 √
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4 χ
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

82. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2 √
(E,G) 3 χ
(C,D) 3 √
(G,H) 3 √
(C,F) 3 √
(B,C) 4 √
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4 χ
(B,F) 4 χ
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

83. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2 √
(E,G) 3 χ
(C,D) 3 √
(G,H) 3 √
(C,F) 3 √
(B,C) 4 √
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4 χ
(B,F) 4 χ
(B,H) 4 χ
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

84. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2 √
(E,G) 3 χ
(C,D) 3 √
(G,H) 3 √
(C,F) 3 √
(B,C) 4 √
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4 χ
(B,F) 4 χ
(B,H) 4 χ
(A,H) 5 √
(D,F) 6
(A,B) 8
(A,F) 10

85. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2 √
(E,G) 3 χ
(C,D) 3 √
(G,H) 3 √
(C,F) 3 √
(B,C) 4 √
5
1
A
H
B
F
E
D
C
G
2
3
3
3
edge dv
(B,E) 4 χ
(B,F) 4 χ
(B,H) 4 χ
(A,H) 5 √
(D,F) 6
(A,B) 8
(A,F) 10
Done
Total Cost = Σ dv = 21
4
}not
considered