Αποκλειστικά από το lisari.blogpsot.gr

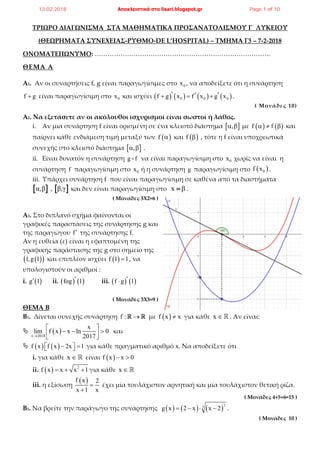
1. ΤΡΙΩΡΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ΄ ΛΥΚΕΙΟΥ
(ΘΕΩΡΗΜΑΤΑ ΣΥΝΕΧΕΙΑΣ-ΡΥΘΜΟ-DE L’HOSPITAL) – ΤΜΗΜΑ Γ3 – 7-2-2018
ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ……………………………………………………………………….
ΘΕΜΑ A
Α1. Αν οι συναρτήσεις f, g είναι παραγωγίσιµες στο 0x , να αποδείξετε ότι η συνάρτηση
f g είναι παραγωγίσιµη στο 0x και ισχύει        0 0 0f g x f x g x     .
( Μονάδες 10)
A2. Να εξετάσετε αν οι ακόλουθοι ισχυρισµοί είναι σωστοί ή λάθος.
i. Αν µια συνάρτηση f είναι ορισµένη σε ένα κλειστό διάστηµα  ,  µε    f f   και
παίρνει κάθε ενδιάµεση τιµή µεταξύ των  f  και  f  , τότε η f είναι υποχρεωτικά
συνεχής στο κλειστό διάστηµα  ,  .
ii. Είναι δυνατόν η συνάρτηση g f να είναι παραγωγίσιµη στο 0x χωρίς να είναι η
συνάρτηση f παραγωγίσιµη στο 0x ή η συνάρτηση g παραγωγίσιµη στο  0f x .
iii. Υπάρχει συνάρτηση f που είναι παραγωγίσιµη σε καθένα από τα διαστήµατα
   α,β , β,γ και δεν είναι παραγωγίσιµη στο x β .
( Μονάδες 3X2=6 )
A3. Στο διπλανό σχήµα φαίνονται οι
γραφικές παραστάσεις της συνάρτησης g και
της παραγώγου f της συνάρτησης f.
Αν η ευθεία (ε) είναι η εφαπτοµένη της
γραφικής παράστασης της g στο σηµείο της
  1,g 1 και επιπλέον ισχύει  f 1 1 , να
υπολογιστούν οι αριθµοί :
i.  g 1 ii.    fog 1 iii.    f g 1
( Μονάδες 3Χ3=9 )
ΘΕΜΑ B
Β1. Δίνεται συνεχής συνάρτηση f :   µε  f x x για κάθε x   . Aν είναι:
  x 2018
x
lim f x x ln 0
2017
 
    
και
    f x f x 2x 1    για κάθε πραγµατικό αριθµό x. Nα αποδείξετε ότι
i. για κάθε x   είναι  f x x 0 
ii.   2
f x x x 1   για κάθε x  
iii. η εξίσωση
 f x 2
x 1 x


έχει µία τουλάχιστον αρνητική και µία τουλάχιστον θετική ρίζα.
( Μονάδες 4+5+6=15 )
Β2. Να βρείτε την παράγωγο της συνάρτησης      
23
g x 2 x x 2    .
( Μονάδες 10 )
13.02.2018 Αποκλειστικά στο lisari.blogspot.gr Page 1 of 10

2. ΘΕΜΑ Γ
Θεωρούµε τη συνεχή συνάρτηση  f : 2,3   για την οποία γνωρίζουµε ότι η γραφική της
παράσταση βρίσκεται ολόκληρη µέσα στο ορθογώνιο ΑΒΓΔ (µέσα ή πάνω στις πλευρές) µε
κορυφές    A 3,3 , 2, 3   και πλευρές παράλληλες στους άξονες xx΄ και yy΄.
Γ1. Να αποδείξετε ότι η γραφική παράσταση της συνάρτησης f τέµνει τη διαγώνιο ΑΓ του
ορθογωνίου. ( Μονάδες 8 )
Γ2. Να αποδείξετε ότι υπάρχει τουλάχιστον ένα  2,3  , τέτοιο ώστε να ισχύει
 
     2f 2 3f 0 5f 1
f
10
  
  . ( Μονάδες 8 )
Γ3. Αν  2,3  και  f 0  , να υπολογίσετε το όριο
 
 
x
xxx
9
f
lim
2 f
 
 
 
   
.
( Μονάδες 9 )
ΘΕΜΑ Δ
Δίνεται συνάρτηση :f   η οποία είναι συνεχής στο  .
Δ1. Αν η f είναι γνησίως αύξουσα, να λύσετε την εξίσωση    2018 2017 f x f x x .
( Μονάδες 5 )
Δ2. Για τον περιορισµό της γνησίως αύξουσας συνάρτησης f στο διάστηµα [α,β], να
αποδείξετε ότι υπάρχει τουλαχ. ένα  ,   µε
2α +β α +β
f(ξ) + f = f + f
3 3 2
      
      
     
.
( Μονάδες 5 )
Δ3. Να αποδείξετε ότι αν η συνάρτηση f είναι παραγωγίσιµη στο 0x 1 , τότε
i. η συνάρτηση h µε  
 
 
2
f x , αν x 1
h x
f 2x 1 , αν x 1
 
 
 
είναι παραγωγίσιµη στο 0x 1 .
( Μονάδες 5 )
ii. αν επιπλέον ισχύει 2x 1
f(x) (x 1)
lim 2
x 1
  


α. να αποδείξετε οι συναρτήσεις h και        g x 3f x 1 f 1 x 2f 1     έχουν κοινή
εφαπτοµένη. ( Μονάδες 5 )
β. να υπολογίσετε το όριο:
     
 
5 2
x 1
x 1 ln x 1 10 x 1
lim
h x

    
.
( Μονάδες 5 )
Καλή επιτυχία !!!!!!!
13.02.2018 Αποκλειστικά στο lisari.blogspot.gr Page 2 of 10

3. ΑΠΑΝΤΗΣΕΙΣ ΔΙΑΓΩΝΙΣΜΑΤΟΣ
ΛΥΣΗ ΘΕΜΑΤΟΣ A :
Α1. Θεωρία, απόδειξη σελίδα 111
A2. 1  Λ (όπως φαίνεται στο σχήµα στη γραφική
παράσταση της διπλανής συνάρτησης
 
2
2
2 x , αν 1 x 0
f x
1 x , αν 0 x 1
    
     
2 Σ (Για τις συναρτήσεις   2
f x 2x , x  και
 g x x , x  ορίζεται η συνάρτηση gof µε
   2
gof x 2x , x  που είναι παραγωγίσιµη στο
0x 0 ενώ η f είναι παραγωγίσιµη στο 0x 0 και η
g ΔΕΝ είναι παραγωγίσιμη στο  f 0 0 ).
3 Σ (αφού η
παραγωγισιµότητα στα
διαστήµατα    α,β , β,γ δεν
σηµαίνει κατ΄ ανάγκη
παραγωγισιµότητα στο x β .
Όπως στο σχήµα για τη συνεχή
στο x 1 συνάρτηση
 
2
2
1 x , αν 1 x 1
f x
x 4x -3 , αν 1 x 3
    
 
    
που είναι παραγωγίσιµη στα [-1,1] και [1,3] , αφού
   
x 1
f x f 1
lim 2
x 1


 

,
   
x 1
f x f 1
lim 2
x 1




).
A3. Είναι από το σχήµα i.  
3
g 1 150 30
3
 

        
ii. Είναι    g 1 0,f 0 2   και             
3 3 2 3
fog 1 f g 1 g 1 f 0 2
3 3 3
                     
   
iii. Είναι  f 1 1 ,  f 1 3   και            
3 3
f g 1 f 1 g 1 f 1 g 1 3 0 1
3 3
                 
 
ΛΥΣΗ ΘΕΜΑΤΟΣ B :
B1. i. Αρχικά η συνάρτηση    g x f x x  είναι συνεχής στο  ως διαφορά συνεχών και
αφού ισχύει  f x x για κάθε x   θα είναι    g x f x x 0   . Αυτό δίνει ότι η g στο 
διατηρεί πρόσηµο οµόσηµο κάποιας τιµής της. Επειδή η συνάρτηση f είναι συνεχής στο
2018 η σχέση  x 2018
x
lim f x x ln 0
2017
 
    
γράφεται  
2018
f 2018 2018 ln 0
2017
   
 
2018
f 2018 2018 ln 0
2017
    ή  g 2018 0 . Άρα    g x 0 f x x 0    για κάθε x   .
13.02.2018 Αποκλειστικά στο lisari.blogspot.gr Page 3 of 10

4. ii. Η σχέση    f x f x 2x 1    γίνεται
           
22 2 2 2 2 2
f x 2xf x 1 f x 2xf x x 1 x f x x 1 x f x x 1 x                 . Από
το ερώτηµα (B1. i.) όµως είναι  f x x 0  για κάθε x   και έτσι έχουµε
   2 2
f x x 1 x f x x 1 x       για κάθε x   .
iii. Η εξίσωση
 f x 2
x 1 x


για x 0 και x 1   ισοδύναµα γράφεται    xf x 2 x 1 0   .
Ορίζουµε τη συνάρτηση      h x xf x 2 x 1   µε   2
f x x 1 x   για κάθε x   .
Παρατηρούµε ότι  h 0 2 0   και    h 1 f 1 1 2 0       , άρα 0 και (-1) ΔΕΝ είναι ρίζες.
Θα εφαρµόσουµε Θεώρηµα Bolzano για την h στα διαστήµατα [-2,0] και [0,2].
 Η συνάρτηση h είναι συνεχής στα διαστήµατα [-2,0] και [0,2] ως πράξεις συνεχών.
          h 2 2f 2 2 1 2 2 5 2 2 3 5 0              ,    h 0 0 f 0 2 2 0      και
       h 2 2f 2 6 2 2 5 6 2 5 1 0        . Άρα είναι    h 2 h 0 0   και    h 0 h 2 0  .
Έτσι η εξίσωση  h x 0 έχει από µία τουλάχιστον ρίζα στα διαστήµατα (-2,0) (που ΔΕΝ
είναι το (-1)) και (0,2), δηλαδή έχει µία τουλάχιστον αρνητική και µία τουλάχιστον θετική
ρίζα όπως και η ισοδύναµή της
 f x 2
x 1 x


. Υπάρχουν και άλλα διαστήµατα στα οποία
µπορούµε να δουλέψουµε! Π.χ [-2,-1] στα αρνητικά και [1,2] στα θετικά ή άλλα.
Β2. H συνάρτηση γράφεται    
   
   
23
23
23
2 x 2 x , αν x 2
g x 2 x x 2 0 , αν x 2
2 x x 2 , αν x 2
    


     

   
. Έτσι
 Αν x<2 η συνάρτηση g είναι παραγωγίσιµη ως γινόµενο των παραγωγίσιµων
συναρτήσεων  2 x και  
23
2 x ( η συνάρτηση  
23
2 x είναι παραγωγίσιµη ως
σύνθεση των παραγωγίσιµων συναρτήσεων  
2
2 x και 3
x ) µε παράγωγο
               
2 2 1 2
233 3 3 3
2 5 5
g (x) 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x
3 3 3

                       
 
 Αν x>2 η συνάρτηση g είναι παραγωγίσιµη ως γινόµενο των παραγωγίσιµων
συναρτήσεων  2 x και  
23
x 2 ( η συνάρτηση  
23
x 2 είναι παραγωγίσιµη ως
σύνθεση των παραγωγίσιµων συναρτήσεων  
2
x 2 και 3
x ) µε παράγωγο
               
2 2 1 2
233 3 3 3
2 5 5
g (x) 2 x x 2 x 2 2 x x 2 x 2 x 2 x 2
3 3 3

                       
 
.
 Αν x=2 έχουµε

         23
x 2 x 2 x 2
x 22 x 2 x 0g x g 2
lim lim lim
x 2 x 2  
  
    
 
 
 
23
2 x
x 2
 

0

         23
x 2 x 2 x 2
x 22 x x 2 0g x g 2
lim lim lim
x 2 x 2  
  
    
 
 
 
23
x 2
x 2
 

0
Άρα  g 2 0  ή αλλιώς
13.02.2018 Αποκλειστικά στο lisari.blogspot.gr Page 4 of 10

5.          23
x 2 x 2 x 2
x 22 x x 2 0g x g 2
lim lim lim
x 2 x 2  
    
 
 
 
23
x 2
x 2
 

 0 g 2  , οπότε
 
 
 
23
23
23
5
2 x , αν x 2
3
5
g (x) 0 , αν x 2 x 2
3
5
x 2 , αν x 2
3

  

     

  

για κάθε x   .
ΛΥΣΗ ΘΕΜΑΤΟΣ Γ :
Γ1. Το ορθογώνιο µε κορυφές    A 3,3 , 2, 3   και πλευρές
παράλληλες στους άξονες xx΄ και yy΄ έχει τις άλλες κορυφές
του λόγω συµµετρίας να είναι οι  3, 3  και  2,3  .
Επιπλέον, δίνεται ότι η γραφική παράσταση της συνάρτησης f
βρίσκεται ολόκληρη µέσα στο ορθογώνιο ΑΒΓΔ. Αυτό σηµαίνει
ότι ισχύει  3 f x 3   για κάθε  x 2,3  . Η διαγώνιος ΑΓ
έχει συντελεστή διεύθυνσης
 
 
3 3 6
3 2 5

 
  
 
και εξίσωση  
6 6 3
y 3 x 3 y x
5 5 5
      . Για
να δείξουµε ότι η γραφική παράσταση της συνάρτησης f τέµνει τη διαγώνιο ΑΓ του
ορθογωνίου, αρκεί να δείξουµε ότι η εξίσωση    
6 3
f x x 5f x 6x 3 0
5 5
      έχει µια,
τουλάχιστον λύση στο διάστηµα  2,3 . Θεωρούµε τη συνάρτηση    g x 5f x 6x 3   , µε
 x 2,3  , η οποία είναι συνεχής στο διάστηµα  2,3 µε βάση τις ιδιότητες των συνεχών
και επιπλέον ισχύει ότι    g 2 5 f 2 3      . Όµως
       3 f 2 3 0 f 2 3 6 0 5 f 2 3 30 0 g 2 30                    .
Ακόµη    g 3 5 f 3 3    . Όµως    3 f 3 3 6 f 3 3 0        
   30 5 f 3 3 0 30 g 3 0           . Άρα, τελικά    g 2 g 3 0   .
Διακρίνουµε τις περιπτώσεις:
Αν    g 2 g 3 0   τότε η συνάρτηση g πληροί τις υποθέσεις του θεωρήµατος Bolzano στο
διάστηµα  2,3 . Ως εκ τούτου υπάρχει ένα τουλάχιστον  0x 2,3  τέτοιο, ώστε  0g x 0 ,
δηλαδή, τέτοιο, ώστε η γραφική παράσταση της συνάρτησης f να τέµνει τη διαγώνιο ΑΓ
13.02.2018 Αποκλειστικά στο lisari.blogspot.gr Page 5 of 10

6. στο σηµείο   0 0x ,f x ή το 0 0
6 3
x , x
5 5
 
 
 
.
Αν      g 2 g 3 0 g 2 0      ή    g 3 0 f 2 3     ή  f 3 3 , τότε η γραφική
παράσταση της συνάρτησης f τέµνει τη διαγώνιο ΑΓ στα σηµεία  2, 3   και  A 3,3
αντίστοιχα.
Γ2. Δίνεται ότι η συνάρτηση f είναι συνεχής στο  2,3 , ως εκ τούτου, σύµφωνα µε το
θεώρηµα µέγιστης και ελάχιστης τιµής, αυτή θα παίρνει στο διάστηµα αυτό µια ελάχιστη
τιµή m και µια µέγιστη τιµή M . Εποµένως, θα υπάρχουν    1 2x ,x 2,3 τέτοια ώστε αν
 1f x m και  2f x M να ισχύει  m f x M  , για κάθε    x 2,3 . Οπότε θα έχουµε:
m f( 2) M 2m 2f( 2) 2M      
m f(0) M 3m 3f (0) 3M    
m f(1) M 5m 5f (1) 5M    
Προσθέτοντας κατά µέλη τις οµοιόστροφες ανισότητες και διαιρώντας µε 10 προκύπτει ότι:
     2f 2 3f 0 5f 1
m M
10
  
  . Διακρίνουµε τις περιπτώσεις:
Αν m M , τότε η συνάρτηση f είναι σταθερή και για τυχαίο  ξ 2,3  θα ισχύει το
ζητούµενο, δηλαδή, ότι:  
     2f 2 3f 0 5f 1
f ξ
10
  
 .
Αν m M , τότε το σύνολο τιµών της συνάρτησης f είναι το  m,M . Εποµένως αφού
     
 
2f 2 3f 0 5f 1
η m,M
10
  
  θα υπάρχει ένα τουλάχιστον  ξ 2,3  τέτοιο, ώστε:
 
     2f 2 3f 0 5f 1
f ξ
10
  
 .
Γ3. Εφόσον  2,3  και  f 0  , θα ισχύει  0 f 3   και
 
     
1 1 9 9 9
0 f 3 0 0 0 3
3 f 3 f f
           
  
. Διακρίνουµε τις περιπτώσεις:
 Αν  f 3  , τότε το ζητούµενο όριο υπολογίζεται ως εξής:
x
x x
x x x xx x x
9
3 33
lim lim lim
2 3 2 3  
 
    
  x
3
xx x
1
lim 1
22
11
33

 
              
, αφού
x
x
2
lim 0
3
 
 
 
.
 Αν  f 2  , τότε το ζητούµενο όριο υπολογίζεται ως εξής:
x x
x
x x xx x x
9 9
1 92 2
lim lim lim
2 2 2 2 2 4  
   
               
     
, αφού
x
x
9
lim
4
 
  
 
.
 Αν  0 f 2   , τότε το ζητούµενο όριο υπολογίζεται ως εξής:
13.02.2018 Αποκλειστικά στο lisari.blogspot.gr Page 6 of 10

7.  
 
 
     
x x
x
x xxxx x x
x
9 9
f f 9 1
lim lim lim
2 f2 f ff
12 1
22
  
    
    
             
                    
      
, αφού είναι
 
 f
0 f 2 0 1
2

      με
 
x
x
f
lim 0
2
 
 
 
,  
   
9
21 1 9 9
0 f 2
2 f 4 2f

       
 
 
9 9
1
4 2f
  

οπότε
 
x
x
9
lim
2 f
 
  
  
.
 Αν  2 f 3   , τότε το ζητούµενο όριο υπολογίζεται ως εξής:
 
 
 
 
 
 
 
x x
x
x x2xxx x x
x
9 9
f f 9 1
lim lim lim
f2 f 22
1f 1
ff
  
    
    
            
                             
, αφού είναι
 
 
   
f 0 21 1 1 2 2
2 f 3 1
3 f 2 3 f
  
        
 
με
 
x
x
2
lim 0
f
 
 
 
και
   
   
9
2 2 2
2 2
1 1 1 9 9
2 f 3 2 f 3 1
9 f 4 f 4

            
 
οπότε
 
x
2x
9
lim
f
 
  
 
.
Τελικά
 
 
 
 
x
xxx
9
f , αν 0 f 3
lim
1 , αν f 32 f
 
 
       
     
.
ΛΥΣΗ ΘΕΜΑΤΟΣ Δ
Δ1. Η εξίσωση    2018 2017 f x f x x γράφεται    f x x f 2018x 2018x   . Ορίζουµε τη
συνάρτηση    g x f x x , x   για την οποία θα αποδείξουµε ότι είναι γνησίως αύξουσα
στο  . Για τυχαία 1 2x ,x  µε 1 2x x έχουµε ότι    1 2f x f x καθώς η f είναι γνησίως
αύξουσα στο  . Προσθέτοντας τις δύο τελευταίες σχέσεις έχουµε
       1 1 2 2 1 2f x x f x x g x g x     που σηµαίνει ότι η g είναι γνησίως αύξουσα στο  ,
άρα και «1-1». Τότε η εξίσωση    f x x f 2018x 2018x   γίνεται
   
g"1 1"
g x g 2018x x 2018x 2017x 0 x 0

       ΜΟΝΑΔΙΚΗ λύση.
13.02.2018 Αποκλειστικά στο lisari.blogspot.gr Page 7 of 10

8. Δ2. Ορίζουµε τη συνάρτηση  
2α +β α +β
h x f(x) + f x -f -f
3 3 2
      
      
     
. Επειδή για την f
ισχύει ότι  x ,   για την f x
3
  
 
 
ισχύει  x ,
3
  
    
 
. Τότε όμως x
3
 
     
3
2 4
x x
3 3 3 3
 
  
        
         . Επειδή
4 3
3 3 3 3
         
       ,
2
6 4 2 3 3 6
3 2
    
                 που ισχύει καθώς    . Συναληθεύοντας λοιπόν
τις σχέσεις  x ,   και
2 4
x
3 3
     
  έχουμε
2
x
3
 
   . Εφαρμόζουμε λοιπόν το Θεώρημα
Bolzano για τη συνάρτηση h στο διάστημα
2
,
3
  
 
 
. Έτσι
 Η συνάρτηση h είναι συνεχής στο διάστημα
2
,
3
  
 
 
ως άθροισμα των συνεχών συναρτήσεων
2α +β α +β
f(x),f x ,-f -f
3 3 2
      
     
     
(σταθερή), µε τη συνάρτηση f x
3
  
 
 
συνεχή ως
σύνθεση των συνεχών συναρτήσεων x
3
 
 και f .

2 2
h f
3 3
      
   
   
2 2α +β
+ f -f
3 3 3
      
   
   
 
α +β α +β
-f f -f 0
2 2
   
     
   
καθώς
 
   
f ,
α +β
f f f -f 0
2 2 2
 
      
            
   

. Επίσης είναι
 
0 0
2α +β α +β α +β 2 2α +β
h f( ) +f -f -f f( )-f + f -f 0
3 3 2 2 3 3
 
               
                 
            
γιατί
είναι
 
   
f ,
α +β
f f f -f 0
2 2 2
 
      
            
   

και
2 2α +β
f -f 0
3 3
     
    
   
 f ,
2 2α +β 2 2α +β
f f 2 2α +β
3 3 3 3
 
        
               
   

που ισχύει.
Έτσι υπάρχει τουλάχιστον ένα  
2
, ,
3
  
     
 
τέτοιο ώστε  h 0  
2α +β α +β 2α +β α +β
f(ξ) +f -f -f 0 f (ξ) + f = f + f
3 3 2 3 3 2
              
                
           
.
Αλλιώς εναλλακτικά μπορούμε να δουλέψουμε με Θεώρημα Bolzano για την f στο
2
,
3 2
    
  
.
Δ3. Αφού η συνάρτηση f είναι παραγωγίσιµη στο 0x 1 υπάρχει στο  το όριο
 
       
x 1 x 1
f x f 1 f x f 1
f 1 lim lim
x 1 x 1 
 
 
  
 
(σχέση 1) Τότε είναι
i. 
       2
x 1 x 1
f x f 1h x h 1
lim lim
x 1 x 1 
 


 
. Στην περίπτωση του ορίου αυτού µπορούµε να
θεωρήσουµε ότι  x 0,1 , οπότε θέτοντας
x 0
2
u x x u

   µε 2
x 1 x 1
lim u lim x 1 
 
  έχουµε
13.02.2018 Αποκλειστικά στο lisari.blogspot.gr Page 8 of 10

9.                
  
 
2
x 1 x 1 u 1 u 1
f x f 1h x h 1 f u f 1 f u f 1
lim lim lim lim u 1
x 1 x 1 u 1 u 1 u 1
   
   
        
     
 
   
   u 1
f u f 1
lim u 1 2f 1
u 1

 
   
 
.
Αλλιώς
           
   
2 2
2
x 1 x 1 x 1
f x f 1 f x f 1h x h 1
lim lim lim x 1 f 1 2
x 1 x 1 x 1  
  
  
     
    
, γιατί  x 1
lim x 1 2

 
και θέτοντας 2
u x µε 2
x 1 x 1
lim u lim x 1 
 
  είναι
       
 
2
2
x 1 u 1
f x f 1 f u f 1
lim lim f 1
x 1 u 1 
 
 
 
 
.

       
x 1 x 1
h x h 1 f 2x 1 f 1
lim lim
x 1 x 1 
 
  

 
. Στην περίπτωση του ορίου αυτού θέτουµε
v 1
v 2x 1 x
2

    µε  x 1 x 1
lim v lim 2x 1 1 
 
   έχουµε
   
x 1
h x h 1
lim
x 1




               
 x 1 v 1 v 1 v 1
f 2x 1 f 1 f v f 1 f v f 1 f v f 1
lim lim lim lim 2 2f 1
v 1 v 1x 1 v 11
2 2
   
   
     
        
.
Από τα παραπάνω η συνάρτηση h παρατηρούµε ότι είναι παραγωγίσιµη στο 0x 1 µε
   h 1 2f 1  και    h 1 f 1 .
ii. Η συνάρτηση f είναι παραγωγίσιµη άρα και συνεχής στο 0x 1 . Έτσι
     2
2x 1 x 1 x 1
f(x) (x 1) (x 1) 1
f 1 limf(x) lim f (x) (x 1) (x 1) lim x 1
x 1 x 1 x 1  
      
                
1
2 0 0
2
 
    
 
ή  f 1 0 καθώς
 
x 1
u x 1
x 1 limu 0 u 0
x 1 u
lim lim 1
x 1 u
 
  
  
 

. Επίσης  
   
x 1
f x f 1
f 1 lim


 
x 1


 2x 1 x 1
f(x) (x 1) (x 1) f(x) (x 1) (x 1)
lim lim x 1 2 2 1 5
x 1 x 1 x 1 
             
               
. Έτσι είναι
   h 1 2f 1 2 5 10     ,    h 1 f 1 0  και η εφαπτοµένη της Ch στο   A 1,h 1 ή  A 1,0 έχει
εξίσωση  y h 1     h 1 x 1 y 10 x 1 y 10x 10        .
Επίσης η συνάρτηση g µε            g x 3f x 1 f 1 x 2f 1 3f x 1 f 1 x 10          είναι
παραγωγίσιµη στο 0 ως πράξεις παραγωγωγίσιµων καθώς οι συναρτήσεις  f x 1 και
 f 1 x είναι παραγωγίσιµες στο 0. Αυτό συµβαίνει γιατί οι συναρτήσεις  1k x x 1  και
 2k x 1 x  είναι παραγωγίσιµες στο 0 και η συνάρτηση f παραγωγίσιµη στο   1f k 0 1
και   2f k 0 1 . Τότε        g 0 3f 1 1 f 1 1 0 2f 1 10          και
13.02.2018 Αποκλειστικά στο lisari.blogspot.gr Page 9 of 10

10.          g 0 3f 1 f 1 2f 1 2f 1 10        µε την εφαπτοµένη της Cg στο   B 0,g 0 ή  B 0, 10
να έχει εξίσωση     y g 0 g 0 x 0 y 10 10x y 10x 10         .
Άρα η εφαπτοµένη της Ch στο   A 1,h 1 και η εφαπτοµένη της Cg στο   B 0,g 0 είναι κοινή
µε εξίσωση y 10x 10  .
iii. Για το όριο
     
 
5 2
x 1
x 1 ln x 1 10 x 1
lim
h x

    
. Αρχικά είναι
     
 
x 1
20u x 1
5 2 5 2
5 6 5lim u 0 D.L.Hx 1 u 0 u 0 u 0 u 0
1
2ln u
ln u 2ln uulim x 1 ln x 1 lim u ln u lim lim lim
u 5u 5u    

 
      
      

         
   
5
6D.L.H u 0 u 0
2
2ulim lim u 0
25u 25 
 
 
 

 
 
   
 
και      
h ή 1
x 1
lim h x h 1 f 1 0
 

   , οπότε στο όριο
     
 
5 2
x 1
x 1 ln x 1 10 x 1
lim
h x

    
έχουµε απροσδιοριστία
0
0
στην οποία ΔΕΝ µπορούµε να
χρησιµοποιήσουµε κανόνα De L’ Hospital αφού η h και η f ΔΕΝ ξέρουµε αν έχουν συνεχείς
παραγώγους. Έτσι
     
 
   
 
5 42 2
x 1 x 1
x 1 ln x 1 10 x 1 x 1 ln x 1 10
lim lim
h x 0h x
x 1
 
 
        
 


   
     
4 2
x 1
x 1 ln x 1 10 0 10 10
lim 1
h x h 1 h 1 10
x 1


     
    
 

, καθώς όμοια με το προηγούμενο όριο
   
5 2
x 1
lim x 1 ln x 1 0

      
 
είναι και    
4 2
x 1
lim x 1 ln x 1 0

      
 
.
13.02.2018 Αποκλειστικά στο lisari.blogspot.gr Page 10 of 10