More Related Content
Similar to เฉลยแคลคูลัส (20)
More from krurutsamee (20)
เฉลยแคลคูลัส
- 1. เฉลย ใบงานที่ 1
จากฟังก์ชัน y = 2x - 3 เมื่อ x มีค่าเข้าใกล้ 4 ค่าของ f(x) จะเป็นอย่างไร
ก. ค่าของ x เพิ่มขึ้นเข้าใกล้ 4 ข. ค่าของ x ลดลงเข้าใกล้ 4
x f(x) x f(x)
3 3 5 7
3.4 3.8 4.7 6.4
3.7 4.4 4.4 5.8
3.9 4.8 4.1 5.2
3.99 4.98 4.01 5.02
3.999 4.998 4.001 5.002
. . . . . . . . . . . .
ตารางที่ 1 ตารางที่ 2
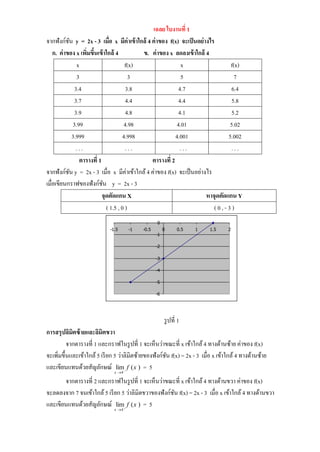
จากฟังก์ชัน y = 2x - 3 เมื่อ x มีค่าเข้าใกล้4 ค่าของ f(x) จะเป็นอย่างไร
เมื่อเขียนกราฟของฟังก์ชัน y = 2x - 3
จุดตัดแกน X หาจุดตัดแกน Y
( 1.5 , 0 ) ( 0 , - 3 )
-6
-5
-4
-3
-2
-1
0
-1.5 -1 -0.5 0 0.5 1 1.5 2
รูปที่ 1
การสรุปลิมิตซ้ายและลิมิตขวา
จากตารางที่ 1 และกราฟในรูปที่ 1 จะเห็นว่าขณะที่ x เข้าใกล้4 ทางด้านซ้าย ค่าของ f(x)
จะเพิ่มขึ้นและเข้าใกล้5 เรียก 5 ว่าลิมิตซ้ายของฟังก์ชัน f(x) = 2x - 3 เมื่อ x เข้าใกล้4 ทางด้านซ้าย
และเขียนแทนด้วยสัญลักษณ์ )(lim
4
xf
x
= 5
จากตารางที่ 2 และกราฟในรูปที่ 1 จะเห็นว่าขณะที่ x เข้าใกล้4 ทางด้านขวา ค่าของ f(x)
จะลดลงจาก 7 จนเข้าใกล้5 เรียก 5 ว่าลิมิตขวาของฟังก์ชัน f(x) = 2x - 3 เมื่อ x เข้าใกล้4 ทางด้านขวา
และเขียนแทนด้วยสัญลักษณ์ )(lim
4
xf
x
= 5
- 2. 2
เฉลยแบบฝึกทักษะที่ 1.1
แบบที่ 1 ฟังก์ชันของพหุนาม
1. 3
lim
x
x2
+ 5x – 3 = 11
2. 3
lim
x
2x2
– x – 7 =14
3. 1
lim
x
(x+3) (x-4) (x2
– 1 ) = 0
4. 4
lim
x
52
xx = 5
5. 3
lim
x
852
xx = 4
6. 4
lim
x
3 23
203 xx = 8
แบบที่ 2 ฟังก์ชันที่มีเศษส่วน
7. 0
lim
x x
xx 2
= - 1
8. 0
lim
x x
xx 63 2
= 6
9. 2
lim
x 6
4
2
2
xx
x
=
5
4
10. 4
lim
x 4
16
2
2
x
x
= 8
11. 3
lim
x 3
273
x
x
= 27
12. 0
lim
h h
xhx 22
4)(4
= 8x
13. 0
lim
h h
xhx 22
12)2(3
= 12x
แบบที่ 3 ฟังก์ชันอยู่ในรูปเศษส่วน
14. 25
lim
x
x
x
5
25
= 10
15. 0
lim
x x
x 416
=
8
1
16. 3
lim
x
21
3
x
x
= 4
17. 1
lim
x
23
1
x
x
= 4
18. 0
lim
x x
x 2
1
2
1
= -
4
1
19. 0
lim
x x
x
4
1
2
1
=
16
1
20. 0
lim
x x
x
cos1
sin2
= 0
แบบที่ 4 ฟังก์ชันที่มีค่าสัมบูรณ์
ให้ f (x) = | x2
– 9 |
21. )(lim
3
xf
x
= 0
22. )(lim
3
xf
x
= 0
23. )(lim
3
xf
x
= 0
24. ให้ f (x) =
x
x ||
1) )(lim
0
xf
x
= - 1
2) )(lim
0
xf
x
= 1
3) )(lim
0
xf
x
= หาค่าไม่ได้
24. ให้ f (x) =
2
|4| 2
x
x
1) )(lim
2
xf
x
= - 4
2) )(lim
2
xf
x
= 4
3) )(lim
2
xf
x
= หาค่าไม่ได้
- 3. 3
เฉลยแบบฝึกทักษะที่ 1.1 ลิมิต (ต่อ) เฉลยใบงานที่ 1.2 ต่อเนื่อง
แบบที่ 5 ฟังก์ชันมีหลายเงื่อนไข
26. ตอบ 4
27. ตอบ 9
28. ตอบ ไม่มีลิมิต
29. ตอบ 5
30. ตอบ 0
1. ต่อเนื่อง
2. ไม่ต่อเนื่อง
3. ไม่ต่อเนื่อง
4. ไม่ต่อเนื่อง
5. ไม่ต่อเนื่อง
6. ต่อเนื่อง
7. ไม่ต่อเนื่อง
8. ไม่ต่อเนื่อง
9. ต่อเนื่อง
10. ต่อเนื่อง
11. หาลิมิตของฟังก์ชันจากกราฟ
1. ตอบ 1
2. ตอบ 1
3. ตอบ 2
4. ตอบ 2
5. ตอบ 4
6. ตอบ 2
7. ตอบ 1
8. ตอบ หาค่าไม่ได้
9. ตอบ 4
10 ตอบ 0
- 4. 4
เฉลยแบบฝึกทักษะที่ 2.1
1. จงหาอัตราการเปลี่ยนแปลงเฉลี่ยของ y เทียบกับ x
1.
35
35
)(f)(f
=
2
2674
= 24
2.
13
13
)(f)(f
=
2
62 )(
= 2
3.
25
25
)(f)(f
=
3
1061
= 17
4.
24
24
)(f)(f
=
2
941
= 16
5.
35
35
)(f)(f
=
2
935
= 13
2. จงหาอัตราการเปลี่ยนแปลงของ y เทียบกับ x ขณะ x ใดๆ
1. 6x ดังนั้น 6(2) = 12
2. 4x + 3 ดังนั้น 4(3) + 3 = 15
3. 2x - 4 ดังนั้น 2(5) - 4 = 6
4. 6x - 2 ดังนั้น 6(4) - 2 = 22
5. 4x - 3 ดังนั้น 4(5) - 3 = 17
3. วงกลมวงหนึ่ง มีรัศมียาว r เซนติเมตร จงหา
1. อัตราการเปลี่ยนแปลงเฉลี่ยของพื้นที่วงกลมเทียบกับความยาวของรัศมี
เมื่อความยาวของรัศมีเปลี่ยนจาก 8 เป็น 10 เซนติเมตร
810
810
)(f)(f
=
2
64100
= 18 ตารางเซนติเมตร/ เซนติเมตร
2. อัตราการเปลี่ยนแปลงของพื้นที่วงกลมเทียบกับความยาวของด้าน ขณะรัศมียาว 8 เซนติเมตร
0
lim
h h
xfhxf )()(
= 2r = 2(8) = 16 ตารางเซนติเมตร/ เซนติเมตร
4. สามเหลี่ยมด้านเท่ารูปหนึ่ง มีด้านยาว x หน่วย จงหา
1. อัตราการเปลี่ยนแปลงเฉลี่ยของพื้นที่เทียบกับความยาวของด้าน
เมื่อความยาวของรัศมีเปลี่ยนจาก 8 เป็น 12 เซนติเมตร
สูตร พื้นที่สามเหลี่ยมด้านเท่า = 2
4
3
x เมื่อ x แทน ความยาวของด้าน
จะได้
812
4
364
4
3144
=
4
320
= 35 ตารางเซนติเมตร/ เซนติเมตร
2. อัตราการเปลี่ยนแปลงของพื้นที่เทียบกับความยาวของด้าน ขณะด้านยาว 12 เซนติเมตร
- 5. 5
0
lim
h h
xfhxf )()(
= x2
4
3
ดังนั้น )(122
4
3
= 36 ตารางเซนติเมตร/ เซนติเมตร
5. ปริมาตรของทรงกลมมีรัศมียาว r เซนติเมตร จงหา
1. อัตราการเปลี่ยนแปลงเฉลี่ยของปริมาตรทรงกลมเทียบกับความยาวของรัศมี
เมื่อความยาวของรัศมีเปลี่ยนจาก 6 เป็น 9 เซนติเมตร
สูตร ปริมาตรทรงกลม =
3
4
r3
69
69
)(f)(f
=
3
288972
=
3
684
= 228 ลูกบาศก์เซนติเมตร/เซนติเมตร
2. อัตราการเปลี่ยนแปลงของปริมาตรทรงกลมเทียบกับความยาวของรัศมี ขณะรัศมียาว 5 เซนติเมตร
0
lim
h h
xfhxf )()(
= 4r2
= 4(5)2
= 100 ลูกบาศก์เซนติเมตร/เซนติเมตร
เฉลยแบบฝึกทักษะที่ 2.2
ชุดที่ 1
1.
dx
dy
= 2
2.
dx
dy
= 5x4
3.
dx
dy
= 6x2
4.
dx
dy
= 8x + 5
5.
dx
dy
= 9x2
– 4x + 1
ชุดที่ 3
11.
dx
dy
= 8x3
– 9x2
+ 2x
12.
dx
dy
= 2x + 6
13.
dx
dy
= 18x – 12
14.
dx
dy
= 12x + 11
15.
dx
dy
=
2
15 xx
- x6
ชุดที่ 2
6.
dx
dy
= 5
4
x
7.
dx
dy
= 3
6
x
8.
dx
dy
= 33
2
x
9.
dx
dy
= 3 2
3
2
x
10.
dx
dy
=
xx
1
16.
dx
dy
= 2x - 3
6
x
17.
dx
dy
= 2
2
6
)x(
18.
dx
dy
=
2
1
19.
dx
dy
= 2
12
4
)x(
20.
dx
dy
= xx2
7 +
2
9 x
+
- 6. 6
เฉลยแบบฝึกทักษะที่ 2.2 (ต่อ)
ชุดที่ 5
21.
dx
dy
= 6(3x + 2)
22.
dx
dy
= 8(2x - 1)3
23.
dx
dy
= 6
23
15
)x(
24.
dx
dy
= 2
21
2
x
x
25.
dx
dy
= 22
2121
2
x)x(
x
ชุดที่ 6
26.
dx
dy
= 24(4x - 1)5
27.
dx
dy
=
xx
x
23
13
2
28.
dx
dy
=
xx)xx(
x
2323
13
22
29.
dx
dy
= 5
3
13
1324
)x(
)x(
30.
dx
dy
= 6
4
12
1220
)x(
)x(
เฉลยแบบฝึกทักษะที่ 2.3 ชุดที่ 1 เส้นสัมผัสเส้นโค้ง
สมการเส้นโค้ง ความชัน (m) สมการเส้นสัมผัส สมการเส้นตั้งฉาก
1. y = x2
– 3x ที่จุด ( 2 , -2 ) m = 1 y = x – 4 x + y = 0
2. y = x - 2x2
ที่จุด ( 2 , - 6 ) m =
3. y = x2
+ 4x - 2 ที่จุด ( - 3 , - 5 ) m = -10 y = -10x – 27 x – 10y + 33 = 0
4. y = (2x- 1 )2
ที่จุด ( 2 , 9 ) m =
5. y =
x
x 22
ที่จุดซึ่ง x = 1 m = - 1 y = - x + 4 y = x + 2
เฉลยแบบฝึกทักษะที่ 2.3 ชุดที่ 2
1. จุดที่สัมผัสเส้นโค้ง คือ (3 , - 4)
2. จุดที่สัมผัสเส้นโค้ง คือ (-2 , - 15)
3. จุดที่สัมผัสเส้นโค้ง คือ (3 , 15)
4. จุดที่สัมผัสเส้นโค้ง คือ (3 , 15)
- 7. 7
5. ค่าของ 2a = 6 , a = 3
6. สมการเส้นตรงที่ตั้งฉากกับเส้นสัมผัสเส้นโค้ง คือ
7. จุดบนเส้นโค้ง y = x3
– 3x คือ (1 , -2 ) และ (- 1 , 2 )
8. จุดบนเส้นโค้ง y = x3
– 27x คือ (3 , - 54 ) และ (- 3 , 54 )
เฉลยแบบฝึกทักษะที่ 2.4
1. กาหนดให้ S แทนระยะทาง (เมตร) t แทนเวลา ( วินาที) v แทนความเร็ว ( เมตร/วินาที )
วัตถุชิ้นหนึ่ง มีสมการของการเคลื่อนที่เป็น S = t2
- 2t + 3 จงหา
1) อัตราการเปลี่ยนแปลงของระยะทางเทียบกับเวลา ตั้งแต่ t = 2 ถึง t = 5 วินาที
ตอบ 5 เมตร/วินาที
2) อัตราการเปลี่ยนแปลงของระยะทางเทียบกับเวลาขณะเวลา t = 3 วินาที ( ความเร็ว)
ตอบ 4 เมตร/วินาที
2. วัตถุชิ้นหนึ่งเคลื่อนที่ด้วยความเร็วต้น 96 ฟุต/วินาที มีสมการของการเคลื่อนที่เป็น S = 96 t – 8 t2
จงหา
1) ความเร็วเฉลี่ยในช่วงเวลา t = 2 ถึง t = 4
ตอบ 48 ฟุต/วินาที
2) ความเร็วขณะเวลา t = 5 วินาที
ตอบ 16 ฟุต/วินาที
3) ระยะทางที่ก้อนหินขึ้นไปได้สูงสุด
ตอบ t = 6 วินาที , S = 288 ฟุต/วินาที
4) เมื่อใดที่ก้อนหินขึ้นไปได้สูง 256 ฟุต
ตอบ t = 4 , 8 วินาที
5) ความเร่งของวัตถุขณะเวลา t = 3 วินาที
ตอบ -16 ฟุต/วินาที2
3. วัตถุชิ้นหนึ่ง มีสมการของการเคลื่อนที่เป็น S = t3
– 6t2
+ 9t + 4 จงหา
1) ความเร็วเฉลี่ยในช่วงเวลา t = 2 ถึง t = 4
ตอบ 1 เมตร/วินาที
2) ความเร็วขณะเวลา t = 6 วินาที
ตอบ 45 เมตร/วินาที
3) ระยะทางเมื่อความเร็วของวัตถุเท่ากับ 0
ตอบ t = 4 , 8 วินาที
4) เมื่อใดที่ก้อนหินขึ้นไปได้สูง 128 เมตร
ตอบ t = 4 , 8 วินาที
5) ความเร่งของวัตถุขณะเวลา t = 3 วินาที
- 8. 8
ตอบ 6 เมตร/วินาที2
เฉลยแบบฝึกทักษะที่ 2.5
1. จงหาค่าต่าสุดสัมพัทธ์หรือค่าสูงสุดสัมพัทธ์ของฟังก์ชันต่อไปนี้
1) y = x2
– 4x – 2
ตอบ จุดต่าสุดคือ (2 , - 6)
2) y = 2x2
– 8x + 3
ตอบ จุดต่าสุดคือ (2 , - 5)
3) y = 4x – x2
ตอบ จุดสูงสุดคือ (2 , 4)
4) y = - 3x2
– 18x – 20
ตอบ จุดสูงสุดคือ (- 3 , 7)
5) y = x2
– 6x + 5
ตอบ จุดต่าสุดคือ (3 , 4)
6) y = 6 – 2x – x2
จุดสูงสุดคือ
7) y = x3
– 27x
ตอบ ค่าต่าสุดคือ
ค่าสูงสุดคือ
8) y = 12x – x3
ตอบ ค่าต่าสุดคือ
ค่าสูงสุดคือ
9) y = x3
– 3x2
– 9x + 1
ตอบ จุดต่าสุดคือ (3 , - 26)
จุดสูงสุดคือ (- 1 , 6)
10) y = 2x3
– 9x2
+ 12 x – 3
ตอบ จุดต่าสุดคือ (2 , 1)
จุดสูงสุดคือ (1 , 2)
11) y = ( x- 2 )3
ตอบ กรณีที่ 3 ถ้า f /
( c ) = 0
ไม่มีค่าต่าสุดและค่าสูงสุด
12) y = x ( 12 – 2x )2
ตอบ จุดต่าสุดคือ (6 , 0)
จุดสูงสุดคือ (2 , 128)
13) y = x3
– 3x
ตอบ จุดต่าสุดคือ (1 , - 2)
จุดสูงสุดคือ (- 1 , 2)
14) y = 2x3
+ 3x2
– 12x – 7
ตอบ จุดต่าสุดคือ (1 ,-14)
จุดสูงสุดคือ ( - 2 , 13)
15) y = x3
+ x2
– 8x - 1
ตอบ จุดต่าสุดคือ (-2 , 11)
จุดสูงสุดคือ (
3
4
,
27
203
)
- 9. 9
เฉลยแบบฝึกทักษะ1 คน 1 ข้อ ชุดที่ 2.1
ให้ y = f(x) เป็นสมการของเส้นโค้ง ที่ผ่านจุด ( 2 , - 1 ) จงหา
สมการเส้นโค้ง ความชันของเส้นโค้ง สมการของเส้นสัมผัสโค้ง สมการของเส้นที่ตั้งฉาก
1. y = x2
+ x
2. y = x2
- x
3. y = x2
+ 2x
4. y = x2
- 2x
5. y = x2
+ 3x
6. y = x2
- 3x
7. y = x2
+ 5x
8. y = x2
- 5x
9. y = x2
+ 6x
10. y = x2
- 6x
5
3
6
2
7
1
9
-1
10
-2
y = 5x – 11
y = 3x – 7
y = 6x – 13
y = 2x – 5
y = 7x – 15
y = x – 3
y = 9x – 19
y = - x + 1
y = 10x – 21
y = -2x + 3
x + 5y + 3 = 0
x + 3y + 1 = 0
x + y + 4 = 0
x + 2y = 0
x + 7y + 5 = 0
x + y - 1 = 0
x + 9y + 7 = 0
x - y - 3 = 0
x + 10y + 8 = 0
x - 2y - 4 = 0
11. y = 2x2
+ x
12. y = 2x2
– x
13. y = 2x2
+ 3x
14. y = 2x2
– 3x
15. y = 2x2
+ 5x
16. y = 2x2
- 5x
17. y = 3x2
+ x
18. y = 3x2
- x
19. y = 3x2
+ 2x
20. y = 3x2
- 2x
9
7
11
5
13
3
13
11
14
10
y = 9x – 19
y = 7x – 15
y = 11x – 23
y = 5x – 11
y = 13x – 27
y = 3x – 7
y = 13x – 27
y = 11x – 23
y = 14x – 29
y = 10x –21
x + 9y + 7 = 0
x + 7y + 5 = 0
x + 11y + 9 = 0
x + 5y + 3 = 0
x + 13y + 11 = 0
x + 3y + 1 = 0
x +13y +11 = 0
x + 11y + 9 = 0
x + 14y + 12 = 0
x + 10y + 8 = 0
21. y = 3x2
+ 4x
22. y = 3x2
- 4x
23. y = 3x2
+ 5x
16
8
17
y = 16x – 33
y = 8x – 17
y = 17x – 35
x + 16y + 14 = 0
x + 8y + 6 = 0
x + 17y + 15 = 0
- 10. 10
24. y = 3x2
- 5x
25. y = 4x2
+ x
26. y = 4x2
- x
27. y = 4x2
+ 2x
28. y = 4x2
- 2x
29. y = 4x2
+ 3x
30. y = 4x2
- 3x
7
17
15
18
14
19
13
y = 7x – 15
y = 17x – 35
y = 15x – 31
y = 18x – 37
y = 14x – 29
y = 19x – 39
y = 13x – 27
x + 7y + 5 = 0
x + 17y + 15 = 0
x + 15y + 13 = 0
x + 18y + 16 = 0
x - 14y + 12 = 0
x + 19y + 17 = 0
x + 13y + 11 = 0
เฉลยแบบฝึกทักษะ1 คน 1 ข้อ ชุดที่ 2.1
ให้ y = f(x) เป็นสมการของเส้นโค้ง ที่ผ่านจุด ( 2 , - 1 ) จงหา
สมการเส้นโค้ง ความชันของเส้นโค้ง สมการของเส้นสัมผัสโค้ง สมการของเส้นที่ตั้งฉาก
31. y = x2
- 4x + 3
32. y = x2
+ 6x + 5
33. y = x2
- 6x + 5
34. y = x2
+ 6x + 8
35. y = x2
- 6x + 8
36. y = x2
+ 10 x + 9
37. y = x2
- 10x + 9
38. y = x2
+ 2x - 15
39. y = x2
- 2x - 15
40. y = x2
+ 4x - 24
41. y = 6x2
+ x
42. y = 6x2
- x
43. y = 6x2
+2x
44. y = 6x2
- 2x
45. y = x - x2
46. y = x - 2x2
47. y = x2
+ 5x - 2
48. y = x2
- 5x + 2
49. y = (2x - 1)2
50. y = (1 - 3x)2
21
11
21
19
22
18
23
17
24
16
25
23
26
22
- 3
- 7
9
- 1
12
18
y = 21x – 43
y = 11x – 23
y = 21x – 43
y = 19 x – 39
y = 22x – 45
y = 18x – 37
y = 23x – 47
y = 17x – 35
y = 24x – 49
y =16x – 33
y = 25x – 51
y = 23x – 47
y = 26x – 53
y = 22x – 45
y = - 3x + 5
y = - 7x + 13
y = 9x - 19
y = - x + 1
y = 12x - 25
y = 18x - 37
x + 21y + 19 = 0
x + 117y + 9 = 0
x + 21y + 19 = 0
x + 19y + 17 = 0
x + 22y + 20 = 0
x + 18y +16 = 0
x + 23y + 21 = 0
x + 17y + 15 = 0
x + 24y + 22 = 0
x +16y + 14 = 0
x + 25y + 23 = 0
x + 23y + 21 = 0
x + 26y + 24 = 0
x + 22y + 20 = 0
x - 3y - 5 = 0
x - 7y - 9 = 0
x + 9y + 7 = 0
y = x - 3
x + 12y + 10 = 0
x + 18y + 16 = 0
- 11. 11
เฉลย แบบฝึกทักษะที่ 2.2
คาสั่ง ให้นักเรียนทาแบบฝึกทักษะเรียงตามเลขที่
จงหาจุดต่าสุดหรือจุดสูงสุดของฟังก์ชันต่อไปนี้
1. y = x2
+ 2x จุดต่าสุดคือ ( - 1 , 1 )
2. y = x2
- 2x จุดต่าสุดคือ ( 1 , - 1 )
3. y = x2
+ 4x จุดต่าสุดคือ ( - 2 , - 4 )
4. y = x2
- 4x จุดต่าสุดคือ ( 2 , - 4 )
5. y = x2
+ 6x จุดต่าสุดคือ ( - 3 , - 9 )
6. y = x2
- 6x จุดต่าสุดคือ ( 3 , - 9 )
7. y = x2
+ 8x จุดต่าสุดคือ ( - 4 , - 16 )
8. y = x2
- 8x จุดต่าสุดคือ ( 4 , - 16 )
9. y = x2
+ 10x จุดต่าสุดคือ ( - 5 , - 25 )
10. y = x2
- 10x จุดต่าสุดคือ ( 5 , - 25 )
11. y = 2x - x2
จุดสูงสุดคือ ( 1 , 1 )
12. y = 4x - x2
จุดสูงสุดคือ ( 2 , 4 )
13. y = 6x - x2
จุดสูงสุดคือ ( 3 , 9 )
14. y = 8x - x2
จุดสูงสุดคือ ( 4 , 16 )
15. y = 10x - x2
จุดสูงสุดคือ ( 5 , 25 )
16. y = x2
+ 2x + 1 จุดต่าสุดคือ ( - 1 , 0 )
17. y = x2
- 2x + 1 จุดต่าสุดคือ ( 1 , 0 )
18. y = x2
+ 4x + 4 จุดต่าสุดคือ ( - 2 , 0 )
19. y = x2
- 4x + 4 จุดต่าสุดคือ ( 2 , 0 )
20. y = x2
+ 6x + 9 จุดต่าสุดคือ ( - 3 , 0 )
21. y = x2
- 6x + 9 จุดต่าสุดคือ ( 3 , 0 )
26. y = x2
+ 8x + 12 จุดต่าสุดคือ ( - 4 , - 4 )
27. y = x2
- 8x + 12 จุดต่าสุดคือ ( 4 , - 4 )
28. y = x2
+ 4x – 12 จุดต่าสุดคือ ( - 2 , - 16 )
29. y = x2
- 4x – 12 จุดต่าสุดคือ ( 2 , - 16 )
30. y = x2
+ 4x + 3 จุดต่าสุดคือ ( - 2 , - 1 )
31. y = x2
- 4x + 3 จุดต่าสุดคือ ( 2 , - 1 )
32. y = x2
+ 6x + 5 จุดต่าสุดคือ ( - 3 , - 4 )
33. y = x2
- 6x + 5 จุดต่าสุดคือ ( 3 , - 4 )
34. y = x2
+ 6x + 8 จุดต่าสุดคือ ( - 3 , - 1 )
35. y = x2
- 6x + 8 จุดต่าสุดคือ ( 3 , -1 )
36. y = x2
+ 10 x + 9 จุดต่าสุดคือ ( - 5 , - 16 )
37. y = x2
- 10x + 9 จุดต่าสุดคือ ( 5 , - 16)
38. y = x2
+ 2x – 15 จุดต่าสุดคือ ( - 1 , - 16 )
39. y = x2
- 2x – 15 จุดต่าสุดคือ ( 1 , - 16 )
40. y = x2
+ 4x - 24 จุดต่าสุดคือ ( - 2 , - 28 )
41. y = x2
- 4x - 24 จุดต่าสุดคือ ( 2 , - 28 )
42. y = x2
+ 6x - 16 จุดต่าสุดคือ ( - 3 , - 25 )
43. y = x2
- 6x - 16 จุดต่าสุดคือ ( 3 , - 25 )
44. y = x2
+ 10x - 24 จุดต่าสุดคือ ( - 5, - 49 )
45. y = x2
- 10 x - 24 จุดต่าสุดคือ ( 5 , - 49 )
46. y = 2x2
- 8 x - 3 จุดต่าสุดคือ ( 2 , - 5 )
- 12. 12
22. y = x2
+ 8x + 16 จุดต่าสุดคือ ( - 4 , 0 )
23. y = x2
+ 8x + 16 จุดต่าสุดคือ ( 4 , 0 )
24. y = x2
+ 10x + 25 จุดต่าสุดคือ ( - 5 , 0 )
25. y = x2
- 10x + 25 จุดต่าสุดคือ ( 5 , 0 )
47. y = - 3x2
- 12 x - 5 จุดสูงสุดคือ ( - 2 ,7 )
48. y = 12x - x2
จุดสูงสุดคือ ( 6 , - 36 )
49. y = x2
+ 8x + 7 จุดต่าสุดคือ ( - 4 , - 9 )
50. y = x2
- 8x + 7 จุดต่าสุดคือ ( 4 , - 9 )
เฉลยแบบฝึกหัดที่ 2.5
จงหาค่าต่าสุดสัมพัทธ์หรือค่าสูงสุดสัมพัทธ์ของฟังก์ชันต่อไปนี้
7) f(x) = x3
-27x
วิธีทา จาก f(x) = x3
-27x
f /
(x) = 3x² - 27
0 = 3(x² - 9)
0 = (x+3)(x-3)
ดังนั้นค่าวิกฤตของฟังก์ชันคือ - 3 และ 3
ตรวจสอบค่าวิกฤตโดยใช้อนุพันธ์อันดับที่ 2
f´´ (x) = 6x
f´´ (-3) = -18 < 0
f´´ (3) = 18 > 0
ดังนั้น f มีค่าสูงสุดสัมพัทธ์ที่ x = -3
และค่าสูงสุดสัมพัทธ์คือ
f (-3) = (-3)² - 27(-3)
= -27+81 = 54
F มีค่าต่าสุดสัมพัทธ์ที่ x = 3 และค่าต่าสุดสัมพัทธ์คือ
f (3) = (3)² -27(-3)
= 27-81 = -54
8) f (x) = 12x - x³
วิธีทา จาก f (x) = 12x - x³
f´ (x) = 12 – 3x²
0 = 12 – 3x²
x2
= 4
x = 2
ดังนั้นค่าวิกฤตของฟังก์ชันคือ - 2 และ 2
ตรวจสอบค่าวิกฤตโดยใช้อนุพันธ์อันดับที่2
f´´ (x) = -6x
f´´ (2) = -12 < 0
f´´ (-2) = 12 > 0
ดังนั้น f มีค่าต่าสุดสัมพัทธ์ที่ x = -2
และต่าสุดสัมพัทธ์คือ
f(-2) =12 (-2)-(-2)³ = -16
และ f มีค่าสูงสุดสัมพัทธ์ที่ x = 2
และค่าสูงสุดสัมพัทธ์คือ
f (2) = 12 (2) – (2)³ = 16
- 13. 13
80
70
60
50
40
30
20
10
-10
-20
-30
-40
-50
-60
-70
-80
-90
-160 -140 -120 -100 -80 -60 -40 -20 20 40 60 80 100 120 140 160
f x = x3-27x
30
25
20
15
10
5
-5
-10
-15
-20
-25
-30
-50 -40 -30 -20 -10 10 20 30 40 50
f x = 12x-x3
9) f (x) = x3
- 3x2
- 9x + 1
วิธีทา จาก f (x) = x3
-3x2
-9x + 1
f /
(x) = 3x² - 6x – 9
= 3 (x² - 2x – 3)
= 3(x – 3) ( x + 1)
ถ้า f´(x) = 0 = 3( x – 3) ( x + 1) จะได้
x = 3 หรือ x = -1
ดังนั้นค่าวิกฤตของฟังก์ชันคือ 3 และ -1
ตรวจสอบค่าวิกฤตโดยใช้อนุพันธ์อันดับที่ 2
f´´ (x) = 6x -6 = 6 (x – 1)
f´´ (3) = 12 > 0
f´´ (-1) = -12 < 0
10. f (x) = 2x3
– 9x2
+ 12x - 3
วิธีทา จาก f (x) = 2x3
-9x2
+ 12x -3
f /
(x) = 2x3
– 9x2
+ 12x – 3
= 6 ( x2 –
3x + 2 )
= 6 ( x -2 ) ( x – 1)
= 6 ( x – 2 ) ( x - 1 )
ถ้า f /
( x ) = 0 = 6 ( x -2 ) ( x – 1 )
จะได้ x = 2 หรือ x = 1 ดังนั้นค่าวิกฤตของ
ฟังก์ชัน คือ 2 และ 1
ตรวจสอบค่าวิกฤตโดยใช้อนุพันธ์อันดับที่ 2
f //
( x ) = 12x - 18 = 6 ( 2x - 3 )
f //
( 2 ) = 6 > 0
- 14. 14
ดังนั้น f มีค่าสูงสุดสัมพัทธ์ที่ x = -1 และ
ค่าสูงสุดสัมพันธ์ คือ
f (-1) = (-1)3
– 3(-1)2
– 9(-1) + 1
= -1 -3 +9 +1 = 6
f มีค่าต่าสุดสัมพันธ์ที่ x = 3
และค่าต่าสุดสัมพันธ์ คือ
f (3) = (3)3
– 3 (3)2
-9 (3) + 1
= 27 - 27 - 27 + 1 = - 26
ดังรูปข้างล่าง
f //
( 1 ) = - 6 < 0
ดังนั้น f มีค่าสูงสุดสัมพัทธ์ที่ x = 1 และ
ค่าสูงสุดสัมพัทธ์ คือ
f ( 1 ) = 2 ( 1 )2
- 9 (1 )2
+ 12( 1 ) - 3
= 2 – 9 + 12 – 3 = 2
f มีค่าต่าสุดสัมพัทธ์ที่ x = 2 และ
ค่าต่าสุดสัมพัทธ์คือ
f(2) = 2(2)3
– 9(2)2
– 12(2) - 3
= 16 – 36 + 24 – 3 = 1
25
20
15
10
5
-5
-10
-15
-20
-25
-30
-35
-40
-60 -50 -40 -30 -20 -10 10 20 30 40 50 60
f x = x3-3x2-9x +1
- 15. 15
8
6
4
2
-2
-4
-6
-8
-15 -10 -5 5 10 15
f x = 2x3-9x2 +12x -3
11. f(x) = (x - 2)3
วิธีทา จาก f(x) = (x - 2)3
f /
(x) = 3(x - 2)2
= 3(x - 2)(x - 2)
ถ้า f’(x) = 0 จะได้ x = 2
ตรวจสอบค่าวิกฤตโดยใช้อนุพันธ์อันดับที่ 2
f //
x) = 6x – 12
f //
(2) = 6(2) – 12 = 0 กรณีที่ 3 ถ้า f //
(c) = 0 ไม่สามารถสรุปได้
เนื่องจาก f //
(2) = 0 จะไม่สามารถสรุปได้ว่า f(2) จะเป็นค่าสูงสุดสัมพัทธ์หรือค่าต่าสุดสัมพัทธ์
- 16. 16
8
6
4
2
-2
-4
-6
-8
-15 -10 -5 5 10 15
f x = x-2 3
แบบฝึกหัด 3.1 อินทิกรัลไม่จากัดเขต
ชุดที่ 1
จงหา
1. 4
5x dx = x5
+ c
2. 5
4x dx = 6
3
2
x + c
3. 4
x dx
= 3
3
1
x
+ c
4. 4
3
dx
x = 5
5
3
x + c
ชุดที่ 2 การคูณและการหาร
จงหา
9. 3 2
( 4 )x x x dx = 4
5
5
x
x
+ c
10. dxxxx )46( 32
= x6
+ x4
+ c
11.
5
3
3 2
( )
x
dx
x
= x3
+ 2
1
x
+ c
- 17. 17
5. x xdx = xx2
5
2
+ c
6. 3
4 xdx = 33 xx + c
7. 1
dx
x = 2 x + c
8. 1
2
dx
x = x + c
12. 4
3 1
( )
2
dx
x x
= 3
1
x
- x + c
13. 3 5
2 3
( )dx
x x
= 33 x +
xx
2
ชุดที่ 3 อินทิเกรตโดยการเปลี่ยนตัวแปร
14. 2xdx
15. 3
4 9xdx
16. 4
(3 1)x dx
17. 5
(3 4 )x dx
18. 2 1x dx
19. 2 5xdx
ชุดที่ 4 อินทิเกรตโดยการเปลี่ยนตัวแปร
20. dx)x()xx( 36
62
= 72
6
14
1
)xx( + c
21. 3 5 2
( 3 ) ( 1)x x x dx = 63
3
18
1
)xx( + c
22. 3 5 2
( 6 ) ( 2)x x x dx = 63
6
18
1
)xx( + c
23. 2 4
( 4 ) ( 2)x x x dx = 5
4
10
1
)xx( + c
24. 2 3
1x x dx = 11
9
2 33
x)x( + c
25. 2
3
x
dx
x
= 32
x + c
ชุดที่ 5 ระคน
26. 4
15(3 1)x dx
27. 3
2x
dx
x
28. 5
(3 4 )x dx
29. 3
6xdx
30. 3 1x dx
31. 3 4
( 9 ) ( 3)x x x dx
32.
2
3
1
x
dx
x
แบบฝึกหัด 3.2 โจทย์อินทิกรัลไม่จากัดเขต
ก. สมการเส้นโค้ง
1. จงหาสมการเส้นโค้ง y = f(x) เมื่อกาหนดความชันของเส้นสัมผัสเส้นโค้ง ที่จุด (x,y) ใดๆ และจุดที่เส้น
โค้งผ่านดังนี้
1) 2 5
dy
x
dx
ที่จุด (3 ,- 2) 3) 2
2 3
dy
x x
dx
ที่จุด (3 , 1)
- 18. 18
ตอบ y = x2
- 5x + 4
2) 2
3 2
dy
x x
dx
ที่จุด (- 4 , 3)
ตอบ y = x3
– x2
+ 83
ตอบ
4) 3
4 3 1
dy
x x
dx
ที่จุด (2 , 1)
ตอบ
2. ถ้าอัตราการเปลี่ยนแปลงของความชันของเส้นโค้ง ณ จุด (x,y) ใดๆ เป็น 2
12x จงหาสมการเส้นโค้งเมื่อ
เส้นตรงที่ผ่านจุด (0, 2) และ (3, -1)
3. ให้ ( ) 12f x x จงหาสมการเส้นโค้ง y = f(x) ซึ่งผ่านจุด (1,-2) และเส้นสัมผัสที่จุด P ขนานกับ
เส้นตรง 4x - 2y = 0
ข. สมการการเคลื่อนที่
4. วัตถุชิ้นหนึ่งเคลื่อนที่ตามแนวเส้นตรงจากจุดเริ่มต้น ถ้าความเร่งของวัตถุ ในขณะเวลา t ใดๆ
มีค่าเท่ากับ 12t - 4 และเมื่อ t = 1 จะได้ระยะทาง S = 2 เมตร จงหา
1) ความเร็วของวัตถุขณะเวลา t = 2
2) ระยะทาง เมื่อ t = 2
5. โยนวัตถุขึ้นไปในอากาศในแนวดิ่งด้วยความเร็ว 112 – 32t ฟุต/วินาที กาหนด จงหา
1) สมการการเคลื่อนที่ของวัตถุ
2) วัตถุขึ้นไปได้สูงสุดเมื่อเวลาใด
3) ระยะทางที่วัตถุขึ้นไปได้สูงสุด
4) เมื่อใดที่วัตถุอยู่สูง 96 ฟุต
6. ยอดตึกซึ่งสูงจากพื้นดิน 400 ฟุต ก้อนหินก้อนหนึ่งถูกหย่อนลงมาจงหา
1) เมื่อใดที่ก้อนหินจะตกถึงพื้นดิน
2) ความเร็วขณะที่ก้อนหินตกกระทบพื้นดิน
ค. กาไร-ขาดทุน
- 19. 19
7. การผลิตสินค้าเพื่อไปจาหน่ายของบริษัทแห่งหนึ่งพบว่าอัตราการเปลี่ยนแปลงของกาไรเมื่อเทียบกับ
จานวนสินค้าที่ผลิตไปจาหน่ายเท่ากับ 46 – 4x เมื่อ x คาจานวนชิ้นของสินค้า ถ้าในการผลิตสินค้าไป
จาหน่าย 5 ชิ้น บริษัทได้กาไร 1,100 บาท จงหากาไรที่บริษัทจะได้รับในการผลิตสินค้าไปจาหน่าย 10 ชิ้น
8. ในการลงทุนผลิตสินค้าของโรงงานแห่งหนึ่งพบว่าอัตราการเปลี่ยนแปลงของต้นทุนต่อจานวนสินค้า
เท่ากับ 4x – 30 บาท เมื่อ x คือจานวนชิ้นของสินค้าที่ผลิตได้ถ้าในขณะที่ยังไม่ได้ทาการผลิตต้องมีต้นทุน
คงที่เท่ากับ 40000 บาท (ต้นทุนดังกล่าวเป็นค่าเครื่องมือ เครื่องจักรต่างๆ) จงหาต้นทุนในการผลิตสินค้า
จานวน 10 ชิ้น
9. (Ent’33) บริษัทแห่งหนึ่งขายสินค้า 100 ชิ้น ได้กาไร 6800 บาท โดยมีอัตราการเปลี่ยนแปลงของกาไร
เทียบกับจานวนสินค้าที่ขายได้ของบริษัทคือ 78 - 0.08x เมื่อ x คือจานวนสินค้าที่ขายได้ในการผลิตสินค้านี้
จะมีโอกาสได้กาไรมากที่สุดเท่ากับเท่าไร
10. ตัวแทนจาหน่ายของบริษัทแห่งหนึ่งพบว่าอัตราการเปลี่ยนแปลงของกาไรต่อจานวนสินค้าเท่ากับ 120 + 4x
เมื่อ x คือ จานวนสินค้าที่ผลิตได้ในการจาหน่ายสินค้าตัวแทนจะได้กาไร 100 บาท
เมื่อจาหน่ายสินค้า 2 ชิ้น จงหากาไรที่ตัวแทนจาหน่ายจะได้รับ ถ้าจาหน่ายสินค้า 10 ชิ้น
แบบฝึกหัด 3.3 เรื่อง อินทิกรัลจากัดเขต
- 20. 20
1. อินทิกรัลจากัดเซตของฟังก์ชัน
ชุดที่ 1
จงหา
1.
4
2
)2( x = 12
2.
3
3
)42( x dx = 24
3.
2
2
2
)23( xx dx = 16
4.
3
1
2
)2( xx dx =
3
2
5.
4
1
2
)6( xx dx = 24
6.
2
1
2
)12( xx dx = 3
ชุดที่ 2 สมบัติของอินทิกรัล
จงหา
7.
5
2
)4( dx =
8.
2
2
)32( x dx = 10
9.
1
3
2
)2( xx dx =
10.
0
3
)42( x dx +
3
0
)42( x dx = - 24
11.
3
3
)42( x dx
12.
1
3
2
)423( xx dx = 36
2.พื้นที่ใต้โค้ง
ชุดที่ 3 เส้นตรง
จงหาพื้นที่ที่ปิดล้อมด้วยเส้นตรง
13. y = x จาก x = -4 ถึง x = -2
14. y = x + 5 จาก x = -5 ถึง x = 0
15. y = x – 3 จาก x = -3 ถึง x = 3
16. y = -x + 3 จาก x = -3 ถึง x = 0
17. y = 1 – 2x จาก x = -6 ถึง x = -2
18. y = |x| จาก x = -4 ถึง x = 4
ชุดที่ 4 พาราโบลา
จงหาพื้นที่ที่ปิดล้อมด้วยเส้นโค้ง
19. y = x2
- 4 จาก x = -2 ถึง x = 2
20. y = 4x - x2
จาก x = 1 ถึง x = 4
21. y = x2
- 4x + 3 จาก x = -1 ถึง x = 2
22. y = 3 + 2x - x2
จาก x = -1 ถึง x = 2
23. y = 4 - x2
กับแกน x
24. y = x2
- 4x จาก x = 2 ถึง x = 4
ชุดที่ 5 สมการเส้นโค้ง
จงหาพื้นที่ที่ปิดล้อมด้วยเส้นโค้ง
25. y = x3
จาก x = -3 ถึง x = 2
26. y = (x + 2)3
จาก x = -2 ถึง x = 2
27. y = (x – 2)3
จาก x = -4 ถึง x = -2
28. จงหาพื้นที่ที่ปิดล้อมด้วยเส้นโค้ง y = x2
และเส้นตรง y = x + 3
29. จงหาพื้นที่ที่ปิดล้อมด้วยเส้นโค้ง y = 2 - x2
และเส้นตรง y = -x จาก x = -2 ถึง x = 2
30. จงหาพื้นที่ที่ปิดล้อมด้วยเส้นโค้ง y = 2 - x2
และเส้นตรง y = x จาก x = -2 ถึง x = 1
31. จงหาพื้นที่ที่ปิดล้อมด้วยเส้นโค้ง y = 4 - x2
และเส้นตรง y = x + 2 จาก x = -2 ถึง x = 2
32. จงหาพื้นที่ที่ปิดล้อมด้วยเส้นโค้ง y = 3x3
– x2
– 10x และเส้นตรง y = -x2
+ 2x จาก x = -2 ถึง x = 2
เฉลยใบงานที่ 5.1
- 21. 21
การแยกตัวประกอบของพหุนาม
ตอนที่ 1
การดึงตัวร่วม
1. 4 ( x + 4 )
2. xy ( x – y )
3. 2x3
( xy2
+ 2 )
4. 3x ( x – 2 )
5. 3 ( x3
+ x2
+ 25 )
แบบที่ 4 ax2
bx + c
21. ( 3 x - 4 ) ( 2x + 3 )
22. ( 3x + 4 ) ( 2x – 3 )
23. ( 6 x + 5 ) ( 2x – 3 )
24. ( 4x + 5 ) ( 2 x – 3 )
25. - ( 4x - 5 ) ( 3x + 2 )
= ( - 4x + 5 ) ( 3x + 2 )
= ( 4x - 5 ) ( - 3x - 2 )
แบบที่ 1 x2
bx + c
6. ( x + 6) ( x + 4)
7. ( x + 8) ( x + 3)
8. ( x - 6) ( x - 2)
9. ( x – 4 ) ( x – 3 )
10. ( x – 5 ) ( x – 5 )
แบบที่ 5
26. ( x + 3 )2
27. ( x - 3 )2
28. ( 3x + 8 )2
29. ( 3x - 8 )2
30. ( 2x - 5 )2
แบบที่ 2 x2
bx - c
11. ( x – 6 ) ( x + 2 )
12. ( x – 6 ) ( x + 2 )
13. ( x + 8 ) ( x – 3 )
14. ( x - 8 ) ( x + 3 )
15. ( x + 5 ) ( x – 4 )
แบบที่ 6
31. ( x + 1 ) ( x – 1 )
32. ( x + 2 ) ( x – 2 )
33. ( 3x + 5 ) ( 3x – 5 )
34. ( 2x + 3 ) ( 2x – 3 )
35. ( x + 1 ) ( x – 1 ) ( x + 3 ) ( x – 3 )
แบบที่ 3 ax2
bx + c
16. ( 3x + 1 ) ( 4x + 9 )
17. ( 6x + 1 ) ( 2x + 9 )
18. ( 5x - 4 ) ( 2x – 3 )
19. (3 x - 8 ) ( 3x – 8 )
20. ( 4 x - 5 ) ( 2x – 3 )
แบบที่ 8
36. ( x + 1 ) ( x2
– x + 1 )
37. ( x - 2 ) ( x2
+ 2 x + 4 )
38. ( x - 4 ) ( x2
+ 4 x + 16 )
39. ( 2x + 1 ) ( 4x2
- 2 x + 1 )
40. ( 3x - 2 ) ( 9x2
+ 6 x + 4 )
- 22. 22
แบบทดสอบ ก่อนเรียนและหลังเรียน เรื่องค่าต่าสุดหรือค่าสูงสุด
ชั้นมัธยมศึกษาปีที่ 6
1. ข้อใดเป็นกราฟพาราโบลา
ก. y = 2x + 1 ข. y = x
ค. y = 6x – x2
ง. y = x2
2. ฟังก์ชันในข้อใดไม่มีค่าต่าสุด
ก. y = x2
+ 4 ข. y = x2
- 2x + 1
ค. y = x2
ง. y = x3
3. ฟังก์ชันในข้อใดได้ค่าสูงสุด
ก. y = x2
- 2x + 1 ข. x2
+ 2x + 1
ค. y = 1 - 2x + x2
ง. 1 - 2x - x2
7. ฟังก์ชัน y = 2x2
+ 8x + 3
มีค่าต่าสุด ( ค่า y )คือข้อใด
ก. 5 ข. – 5
ค. 27 ง. - 27
8. ฟังก์ชัน y = - 3x2
- 6x - 1
มีค่าสูงสุด ( ค่า y )คือข้อใด
ก. 2 ข. - 2
ค. 10 ง. – 10
9. ในการเกิดปฏิกิริยาครั้งหนึ่ง หาอุณหภูมิจาก
- 23. 23
4. ฟังก์ชัน y = x2
- 4x + 1
มีจุดต่าสุดคือข้อใด
ก. ( 2 , 3 ) ข. ( 2 , - 3 )
ค. ( - 2 , 9 ) ง. ( - 2 , 1 )
5. ฟังก์ชัน y = 6 + 2x – x2
มีจุดสูงสุดคือข้อใด
ก. ( 1 , 7 ) ข. ( 1 , - 5 )
ค. ( - 1 , 3 ) ง. ( - 1 , 7 )
6. ฟังก์ชัน y = 3 - 2x – x2
มีจุดสูงสุดหรือจุดต่าสุดของฟังก์ชันคือข้อใด
ก. จุดต่าสุดคือ ( 1 , 0 ) ข. จุดสูงสุดคือ( 1 , 0 )
ค. จุดต่าสุดคือ (- 1 , 4 ) ง. จุดสูงสุดคือ( - 1 , 4 )
สมการ = 10 + 2t – 0.2 t2
เมื่อ เป็นอุณหภูมิมีหน่วยเป็นองศาเซลเซียส
และ t มีหน่วยเป็นวินาที อุณหภูมิสูงสุดเท่ากับกี่องศา
ก. 15 ข. 20
ค. 25 ง. 30
10. โยนลูกหินขึ้นไปในอากาศตามแนวดิ่ง
ให้ t มีหน่วยเป็นวินาที S มีหน่วยเป็นฟุต
ถ้าสมการการเคลื่อนที่เป็น S = 96t - 16t2
ระยะทางที่ก้อนหินขึ้นไปได้สูงสุดกี่ฟุต
ก. 72 ข. 144
ค. 288 ง. 432
เฉลยแบบทดสอบ ก่อนเรียนและหลังเรียน เรื่องค่าต่าสุดหรือค่าสูงสุด
1 ค 2 ง 3 ง 4 ข 5 ก
6 ง 7 ข 8 ก 9 ก 10 ข
เฉลยใบงานที่ 2.4
1. ถ้า y = 2x2
+ 5x – 3 เป็นสมการเส้นโค้ง จงหา
1) ความชัน = 3
2) สมการของเส้นสัมผัสเส้นโค้ง y = 3x + 9
3) สมการของเส้นตั้งฉาก x + 3y – 11 = 0
2. a = 3
3. x + 4y – 17 = 0
4. ( 1 , - 2 ) และ ( - 1 , 2 )
5. ( 3 , - 54 ) และ ( - 3 , 54 )
6. ( 3 , - 4 )
7. 1) 5 เมตร / วินาที
- 24. 24
2) 4 เมตร / วินาที
8. ระยะทาง – 72 หน่วย ( ระยะทางมีเครื่องหมายเป็น ลบ แสดงว่าวัตถุกาลังเคลื่อนที่ลง )
9.
1) 1 เมตร / วินาที
2) 8 เมตร และ 4 เมตร
3) 45 เมตร / วินาที
4) 6 เมตร / วินาที2
10
1) 0 ฟุต / วินาที
2) 144 ฟุต
3) – 96 ฟุต/วินาที
4) – 32 ฟุต/วินาที2
เฉลยใบงานที่ 2.5
1. จงหาค่าต่าสุดหรือค่าสูงสุดของฟังก์ชัน
1) ( - 2 , - 7 )
2) (
2
3
,
4
1
)
3) ( - 1 , - 1 )
4) ( 3 , - 4 )
5) ( 2 , - 6 )
6) ( 2 , - 5 )
7) ( 2, 4 )
8) ( - 3 , 7 )
2. x =
3
50
เมตร พื้นที่มากที่สุด เท่ากับ 1250 ตารางเมตร
3. จานวนนั้น คือ 0.5
- 25. 25
4. จานวนทั้งสองคือ 5 และ 5
5. จานวนหนึ่งคือ - 3
6. สูง ( x ) = 2 เมตร ปริมาตรมากที่สุด 320 ลูกบาศก์เซนติเมตร
7. t = 10 วินาที = 30 องศาเซลเซียส
8. f = 12 กิโลกรัมต่อไร่
9. ตั้งราคาไว้15 บาท ขายได้เงินมากที่สุด 22,500 บาท
10. กว้าง 45 หน่วย ยาว 60 หน่วย พื้นที่มากที่สุด 2,700 ตารางหน่วย
11. ต้องผลิตสินค้าสัปดาห์ละ 975 ชิ้น
12. 45 กิโลเมตรต่อชั่วโมง
13. w =
3
a
, d =
3
2
a
14. f = 10 p = 500