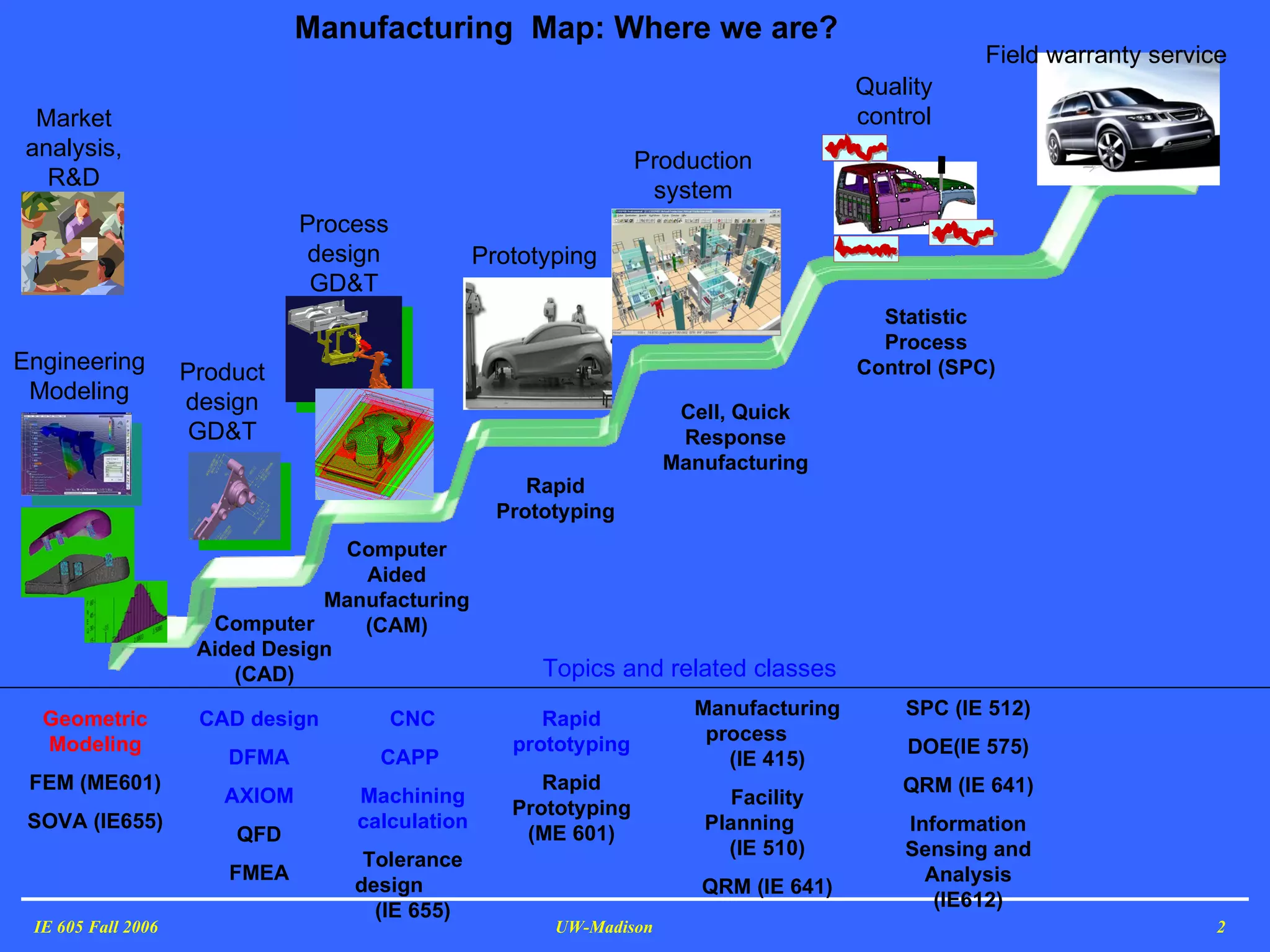
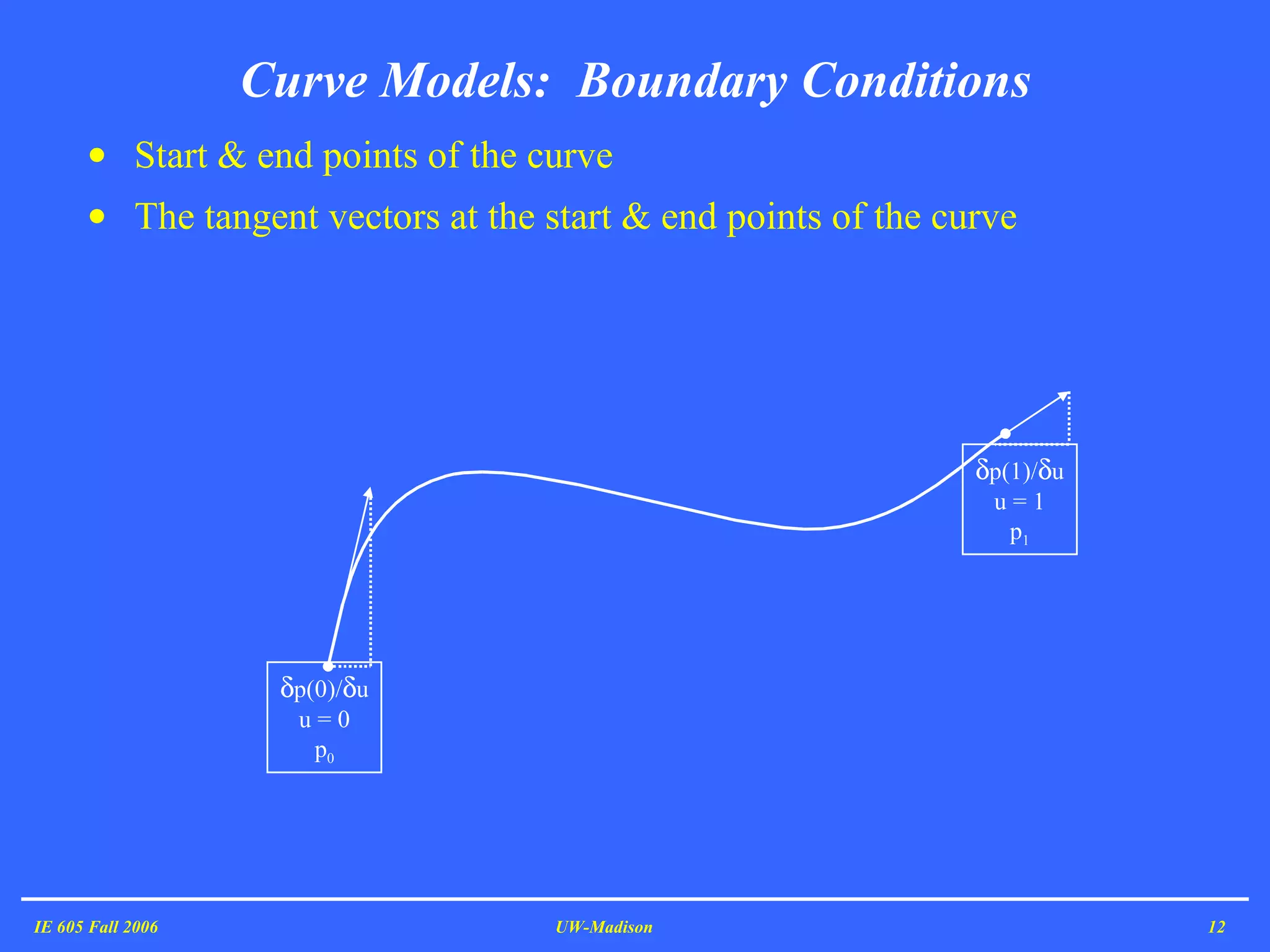
The document discusses geometric modeling which is the foundation of computer-aided design (CAD). It describes the different types of geometric models including graphical models, curve models, surface models, and solid models. Graphical models include wireframe models and can be graphically deficient. Curve models must satisfy boundary conditions at start and end points. When curves are joined, they can have C0, C1 or C2 continuity depending on matching of points, tangents or curvature. The document provides examples of each type of continuity for composite curves.