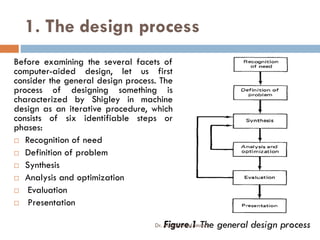
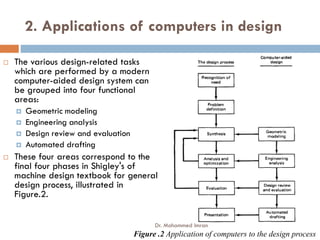
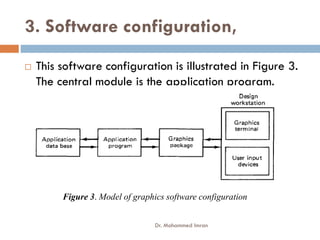
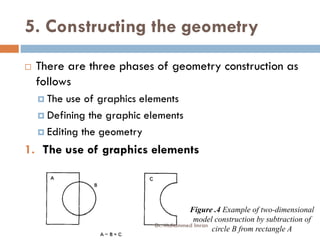
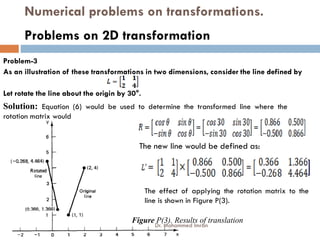
This document outlines the course objectives, outcomes, modules, and content for a Computer Aided Design and Manufacturing course. The key points are: - The course aims to teach students about concepts of computer-integrated manufacturing systems including CAD, CAM, automation, and modern trends like additive manufacturing and Industry 4.0. - The content covers topics like CAD software, geometric modeling, computer-aided process planning, CNC machine tools, and numerical problems involving geometric transformations. - The course objectives are for students to understand CAD/CAM applications, automated manufacturing systems, computer applications in design and manufacturing, and modern manufacturing trends leading to smart factories.

1. COMPUTER AIDED DESIGN AND MANUFACTURING
Course Code 18ME72 CIE Marks 40
Teaching Hours / Week (L:T:P) 3:0:0 SEE Marks 60
Credits 03 Exam Hours 03
[AS PER CHOICE BASED CREDIT SYSTEM (CBCS) SCHEME]
SEMESTER – VII
Dr. Mohammed Imran
B. E. IN MECHANICAL ENGINEERING

2. COMPUTER AIDED DESIGN AND MANUFACTURING
Course Code 18ME72 CIE Marks 40
Teaching Hours / Week (L:T:P) 3:0:0 SEE Marks 60
Credits 03 Exam Hours 03
[AS PER CHOICE BASED CREDIT SYSTEM (CBCS) SCHEME]
SEMESTER – VII
Dr. Mohammed Imran
B. E. IN MECHANICAL ENGINEERING

3. Course Objectives
 To impart knowledge of CIM and Automation and different concepts
of automation by developing mathematical models.
 To make students to understand the Computer Applications in Design
and Manufacturing [CAD / CAM) leading to Computer integrated
systems. Enable them to perform various transformations of entities
on display devices.
To expose students to automated flow lines, assembly lines, Line
 To expose students to automated flow lines, assembly lines, Line
Balancing Techniques, and Flexible Manufacturing Systems.
 To expose students to computer aided process planning, material
requirement planning, capacity planning etc.
 To expose the students to CNC Machine Tools, CNC part
programming, and industrial robots.
 To introduce the students to concepts of Additive Manufacturing,
Internet of Things, and Industry 4.0 leading to Smart Factory.
Dr. Mohammed Imran

4. Course outcomes
On completion of the course the student will be able to
 CO1: Define Automation, CIM, CAD, CAM and explain the differences
between these concepts. Solve simple problems of transformations of
entities on computer screen
 CO2: Explain the basics of automated manufacturing industries
through mathematical models and analyze different types of
automated flow lines.
through mathematical models and analyze different types of
automated flow lines.
 CO3: Analyse the automated flow lines to reduce time and enhance
productivity.
 CO4: Explain the use of different computer applications in
manufacturing, and able to prepare part programs for simple jobs on
CNC machine tools and robot programming.
 CO5: Visualize and appreciate the modern trends in Manufacturing
like additive manufacturing, Industry 4.0 and applications of Internet
of Things leading to Smart Manufacturing.
Dr. Mohammed Imran

5. Module-2
 CAD and Computer Graphics Software: The design process,
applications of computers in design, software configuration,
functions of graphics package, constructing the geometry.
 Transformations: 2D transformations, translation, rotation and
scaling, homogeneous transformation matrix, concatenation,
numerical problems on transformations.
numerical problems on transformations.
 Computerized Manufacture Planning and Control System:
Computer Aided Process Planning, Retrieval and Generative
Systems, benefits of CAPP, Production Planning and Control
Systems, typical activities of PPC System, computer integrated
production management system, Material Requirement
Planning, inputs to MRP system, working of MRP, outputs and
benefits, Capacity Planning, Computer Aided Quality Control,
Shop floor control
10 Hours
Dr. Mohammed Imran

6. Text Books:
 Automation, Production Systems
and Computer-Integrated
Manufacturing, Mikell P Groover,
4 th Edition,2015.
 CAD / CAM Principles and
Applications, P N Rao, 3 rd
Dr. Mohammed Imran
Applications, P N Rao, 3 rd
edition.
 CAD/CAM/CIM, Dr. P.
Radhakrishnan, 3 rd edition.
 Internet of Things (IoT): Digitize
or Die: Transform your
organization. Embrace the digital
evolution. Rise above the
competition, Nicolas
Windpassinger, Amazon Dr. Mohammed Imran

7. Module-2- Part-A
 Chapter-3CAD and Computer Graphics Software:
 The design process,
 Applications of computers in design,
 Software configuration,
 Functions of graphics package,
 Functions of graphics package,
 Constructing the geometry.
 Chapter-4Transformations:
 2D transformations,
 Translation, rotation and scaling,
 Homogeneous transformation matrix,
 Concatenation,
 Numerical problems on transformations.
Dr. Mohammed Imran

8. 1. The design process
Before examining the several facets of
computer-aided design, let us first
consider the general design process. The
process of designing something is
characterized by Shigley in machine
design as an iterative procedure, which
consists of six identifiable steps or
consists of six identifiable steps or
phases:
 Recognition of need
 Definition of problem
 Synthesis
 Analysis and optimization
 Evaluation
 Presentation
Figure.1 The general design process
Dr. Mohammed Imran

9. 2. Applications of computers in design
 The various design-related tasks
which are performed by a modern
computer-aided design system can
be grouped into four functional
areas:
 Geometric modeling
 Engineering analysis
 Engineering analysis
 Design review and evaluation
 Automated drafting
 These four areas correspond to the
final four phases in Shigley's of
machine design textbook for general
design process, illustrated in
Figure.2.
Figure .2 Application of computers to the design process
Dr. Mohammed Imran

10. Fundamental reasons CAD
 There are several fundamental reasons for
implementing a computer-aided design system:
 To Increase the productivity of the designer.
 To improve the quality of design.
 To improve communications.
 To create a data base for manufacturing.
Dr. Mohammed Imran

11. Benefit of CAD
 Improved engineering productivity
 Shorter lead times
 Reduced engineering personnel requirements
 Customer modifications are easier to make
 Faster response to requests for quotations
 Avoidance of subcontracting to meet schedules
 Minimized transcription errors
 Improved productivity in tool design
 Better knowledge of costs provided
 Reduced training time for routine drafting tasks and NC part
programming
 Fewer errors in NC part programming
 Provides the potential for using more existing parts and
tooling
 Helps ensure designs are appropriate to existing
manufacturing techniques
 Minimized transcription errors
 Improved accuracy of design
 In analysis, easier recognition of component
interactions
 Provides better functional analysis to reduce
prototype testing
 Assistance in preparation of documentation
 Designs have more standardization
 Better designs provided
 Helps ensure designs are appropriate to existing
manufacturing techniques
 Saves materials and machining time by optimization algorithms
 Provides operational results on the status of work in progress
 Makes the management of design personnel on projects more
effective
 Assistance in inspection of complicated parts
 Better communication interfaces and greater understanding
among engineers, designers, drafters, management, and
different project groups
Dr. Mohammed Imran

12. 3. Software configuration,
 This software configuration is illustrated in Figure 3.
The central module is the application program.
Figure 3. Model of graphics software configuration
Dr. Mohammed Imran

13. Functions of graphics package
 To fulfill its role in the software configuration, the
graphics package must perform a variety of
different functions.
 Generation of graphic elements
Generation of graphic elements
 Transformations
 Display control and windowing functions
 Segmenting functions
 User input functions
Dr. Mohammed Imran

14. 5. Constructing the geometry
 There are three phases of geometry construction as
follows
 The use of graphics elements
 Defining the graphic elements
 Defining the graphic elements
 Editing the geometry
1. The use of graphics elements
Figure .4 Example of two-dimensional
model construction by subtraction of
circle B from rectangle A
Dr. Mohammed Imran

15. 5. Constructing the geometry
2. Defining the graphic elements:
The user has a variety of different ways to call a particular graphic element and
position it on the geometric model. Table.1 lists several ways of defining points,
lines, arcs, and other components of geometry through interaction with the ICG
(Interactive Computer graphics ) system. These components are maintained in the
data base in mathematical form and referenced to a three-dimensional coordinate
system.
system.
Points
Methods of defining points in computer graphics include:
1. Pointing to the location on the screen by means of cursor control
2. Entering the coordinates via the alphanumeric keyboard
3. Entering the offset (distance in x, y, and z) from a previously defined point
4. The intersection of two points
5. Locating points at fixed intervals along an element
Lines
Methods of defining lines include:
1. Using two previously defined points
2. Using one point and specifying the angle of the line with the horizontal
3. Using a point and making the line either normal or tangent to a curve
4. Using a point and making the line either parallel or perpendicular to another line
5. Making the line tangent to two curves
6. Making the line tangent to a curve and parallel or perpendicular to a line
Table.1 Methods of Defining Elements in Interactive Computer Graphics
Dr. Mohammed Imran

16. 5. Constructing the geometry
2. Defining the graphic elements:
Arcs and Circles
Methods of defining arcs and circles include:
1. Specifying the center and the radius
2. Specifying the center and a point on the circle
3. Making the curve pass through three previously defined points
Table.1 Methods of Defining Elements in Interactive Computer Graphics
3. Making the curve pass through three previously defined points
4. Making the curve tangent to three lines
5. Specifying the radius and making the curve tangent to two lines or curves
Conies
Conies, including ellipses, parabolas, and hyperbolas, can be defined in any plane by methods which include:
1. Specifying five points on the element
2. Specifying three points and a tangency condition
Curves
Mathematical splines are used to fit a curve through given data. For example, in a cubic spline, third-order polynomial segments are fitted between each pair of
adjacent data points. Other curvegenerating techniques used in computer graphics include Bezier curves and B-spline methods. Both of these methods use a
blending procedure which smooths the effect of the data points. The resulting curve does not pass through all the points. In these cases the data points would be
entered to the graphics system and the type of curve-fitting technique would be specified for determining the curve
Surfaces
The methods described for generating curves can also be used for determining the mathematical definition of a surface. Automobile manufacturers use these
methods to represent the sculptured surfaces of the sheet metal car body. Some of the methods for generating surfaces include:
1. Using a surface of revolution formed by rotating any lines and/or curves around a specific axis.
2. Using the intersection line or surface of two intersecting surfaces.
For example, this could be used to generate cross sections of parts, by slicing a plane through the part at the desired orientation.
Dr. Mohammed Imran

17. 5. Constructing the geometry
3. Editing the geometry:
A computer-aided design system provides editing capabilities to make
corrections and adjustments in the geometric model. When developing the
model, the user must be able to delete, move, copy, and rotate components
of the model. Some Common Editing Features Available on a CAD System.
 Move an item to another location.
 Duplicate an item at another location.
 Rotate an item.
 Mirror an item.
 Remove an item from the display (without deleting it from the data
base).
 Trim a line or other component.
 Create a cell out of graphic elements.
 Scale an item.
Dr. Mohammed Imran

18. Chapter-4 Transformations:
 Many of the editing features involve transformations
of the graphics elements or cells composed of
elements or even the entire model.
 In this section we discuss the mathematics of these
 In this section we discuss the mathematics of these
transformations. Two-dimensional transformations
are considered first to illustrate concepts. Then we
deal with three dimensions
Dr. Mohammed Imran

19. 1. 2D transformations:
 To locate a point in a two-axis Cartesian system, the x and y coordinates
are specified. These coordinates can be treated together as a 1 x 2 matrix:
(x,y).
 For example, the matrix (2, 5) would be interpreted to be a point which is
2 units from the origin in the x-direction and 5 units from the origin in the y-
direction.
 This method of representation can be conveniently extended to define a
 This method of representation can be conveniently extended to define a
line as a 2 × 2 matrix by giving the x and y coordinates of the two end
points of the line. The notation would be
 Using the rules of matrix algebra, a point or line (or other geometric
element represented in matrix notation) can be operated on by a
transformation matrix to yield a new element.
 There are several common transformations used in computer graphics. We
will discuss three transformations: translation, scaling, and rotation.
Dr. Mohammed Imran

20. 1.1 Translation:
 Translation involves moving the element from one location to another. In the case of a
point, the operation would be
where x',y' = coordinates of the translated point
x,y = coordinates of the original point
m,n = movements in the x and y directions, respectively
m,n = movements in the x and y directions, respectively
 In matrix notation this can be represented as
where T = (m,n), the translation matrix ---(5)
 Any geometric element can be translated in space by applying Eq. (4) to each point
that defines the element. For a line, the transformation matrix would be applied to its
two end points.
Dr. Mohammed Imran

21. 1.2. Rotation:
 In this transformation, the points of an object are
rotated about the origin by an angle 0. For a positive
angle, this rotation is in the counterclockwise direction.
This accomplishes rotation of the object by the same
angle, but it also moves the object. In matrix notation,
angle, but it also moves the object. In matrix notation,
the procedure would be as follows:
Dr. Mohammed Imran

22. 1.3. Scaling:
 Scaling of an element is used to enlarge it or reduce its size. The
scaling need not necessarily be done equally in the x and y
directions. For example, a circle could be transformed into an ellipse
by using unequal x and y scaling factors.
 The points of an element can be scaled by the scaling matrix as
follows:
follows:
Where
 This would produce an alteration in the size of the element by the
factor m in the x-direction and by the factor n in the y- direction
Dr. Mohammed Imran

23. 2. Three-dimensional transformations
 Transformations by matrix methods can be extended to three-dimensional space.
We consider the same three general categories defined in the preceding section.
The same general procedures are applied to use these transformations that were
defined for the three cases by Eqs. (4), (6), and (8).
2.1 Translation: The translation matrix for a point defined in three dimensions would
be
2.2 Rotation: Rotation in three dimensions can be defined for each of the axes.
2.2 Rotation: Rotation in three dimensions can be defined for each of the axes.
Rotation about the z axis by an angle  is accomplished by the matrix
 Rotation about the y axis by the angle  is accomplished similarly
 Rotation about the x axis by the angle  is done with an analogous transformation
matrix.
Dr. Mohammed Imran

24. 2. Three-dimensional transformations
 2.3 Scaling: The scaling transformation is given by
For equal values of m, n, and p, the scaling is linear
For equal values of m, n, and p, the scaling is linear
Dr. Mohammed Imran

25. 3. Concatenation,
 The previous single transformations can be combined as a sequence of
transformations. This is called concatenation, and the combined transformations are
called concatenated transformations.
 During the editing process when a graphic model is being developed, the use of
concatenated transformations is quite common. It would be unusual that only a single
transformation would be needed to accomplish a desired manipulation of the
image.
image.
 Two examples of where combinations of transformations would be required would
be:
 Rotation of the element about an arbitrary point in the element.
 Magnifying the element but maintaining the location of one of its points in the same location.
 In the first case, the sequence of transformations would be: translation to the origin,
then rotation about the origin, then translation back to the original location.
 In the second case, the element would be scaled (magnified) followed by a
translation to locate the desired point as needed.
 The objective of concatenation is to accomplish a series of image manipulations as a
single transformation. This allows the concatenated transformation to be defined
more concisely and the computation can generally be accomplished more efficiently.
Dr. Mohammed Imran

26. Numerical problems on transformations.
Problem-1
As an illustration of these transformations in two dimensions, consider the line defined by
Let us suppose that it is desired to translate the line in space by 2 units in the x direction and 3 units in the
y direction.
Problems on 2D transformation
Solution: This would involve adding 2 to the current x value and 3 to the current y
value of the end points defining the line. That is
value of the end points defining the line. That is
Figure P(1). Results of translation
The new line would have end points at (3, 4) and (4, 7).
The effect of the transformation is illustrated in Figure
P(1).
Dr. Mohammed Imran

27. Numerical problems on transformations.
Problem-2
As an illustration of these transformations in two dimensions, consider the line defined by
let us apply the scaling factor of 2 to the line.
Problems on 2D transformation
Solution: The scaling matrix for the 2 x 2 line definition would therefore be
Figure P(2). Results of translation
The resulting line would be determined
by Eq. (8) as follows:
The new line is pictured in Figure P(2).
Dr. Mohammed Imran

28. Numerical problems on transformations.
Problem-3
As an illustration of these transformations in two dimensions, consider the line defined by
Let rotate the line about the origin by 30°.
Problems on 2D transformation
Solution: Equation (6) would be used to determine the transformed line where the
rotation matrix would
rotation matrix would
Figure P(3). Results of translation
The new line would be defined as:
The effect of applying the rotation matrix to the
line is shown in Figure P(3).
Dr. Mohammed Imran

29. Numerical problems on transformations.
Problem-4
Let us consider the example cited in the text in which a point was to be scaled by a factor of 2
and rotated by 45°. Suppose that the point under consideration was (3, 1). This might be one
of several points defining a geometric element. For purposes of illustration let us first
accomplish the two transformations sequentially. First, consider the scaling
Problems on Concatenation
Dr. Mohammed Imran

30. Problem-4
Problems on Concatenation
Dr. Mohammed Imran