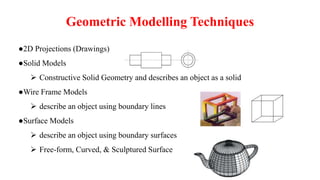
This document discusses different techniques for geometric modelling. It describes wireframe modelling as using points, lines, arcs and curves to represent an object. Surface modelling uses faces defined by wireframes to represent surfaces. Solid modelling defines objects by their enclosed volume using half-spaces. The document provides examples of how varying parameters like radius, angle, and height in equations can represent different geometric objects like circles, cylinders, disks, and solid or hollow cylinders.

2. Geometric Modelling
• Modelling- Creating symbolic models of the physical world has long
been a goal of mathematicians, scientists, engineers, etc.
• Geometrical Modelling can be defined as computer friendly and
mathematical representation of geometry.
• Geometric Modelling is the computer-aided design and manipulation of
geometric objects.
• Geometric modelling is only a means not the goal in engineering.

3. ●2D Projections (Drawings)
●Solid Models
 Constructive Solid Geometry and describes an object as a solid
●Wire Frame Models
 describe an object using boundary lines
●Surface Models
 describe an object using boundary surfaces
 Free-form, Curved, & Sculptured Surface
Geometric Modelling Techniques

4. ●Wireframe Modelling (Auto-cad Drawings)
• The word “wireframe” is related to the fact that one may
imagine a wire that is bent to follow the object edges to generate
a model.
• Developed in 1960s and referred as “a stick figure” or “an
edge representation”
• Model consists entirely of points, lines, arcs and circles,
conics, and curves.
Wireframe Modelling

5. ●Advantages
• Simple to construct
• Does not require as much as computer time and memory as does surface or solid modelling.
• As a natural extension of drafting, it does not require extensive training of users.
• From the basis for surface modelling as most surface algorithms require wireframe entities
(such as points, lines and curves)
●Disadvantages
• The input time is substantial and increases rapidly with the complexity of the object
• Both topological and geometric data need to be user-input; while solid modelling requires only
the input of geometric data.
• volume and mass properties, NC tool path generation, cross-sectioning, and interference cannot
be calculated.
Wireframe Modelling

6. ●Surface Modelling
• A surface model is a set of faces.
• A surface model consists of wireframe entities that form
the basis to create surface entities.
• Used to be separated, shape model are now incorporated
into solid models.
• It is most often used type of model.
Surface Modelling

7. ●Examples of Surface Modelling
• Surface models define only the geometry, no topology.
• Shading is possible.
Surface Modelling

8. ●Advantages
• Less ambiguous
• Provide hidden line and surface algorithms to add realism to the displayed geometry
• Support volume and mass calculation, finite element modelling, NC path generation, cross
sectioning, and interference detection.
●Disadvantages
• Require more training and mathematical background of the users
• Require more CPU time and memory.
• Awkward to construct.
Surface Modelling

9. ●Solid Modelling
• The solid modelling technique is based upon the "half-
space” concept.
• The object is defined by the volume space contained
within the defined boundary of the object.
• In general speaking, a closed boundary is needed to
define a solid object.
Solid Modelling

10. ●Solid Modelling Support
• Using volume information
– weight or volume calculation, centroids, moments of
inertia calculation,
– stress analysis (finite elements analysis), heat conduction calculations,
– system dynamics analysis
• Using volume and boundary information
– generation of CNC codes, and robotic and assembly simulation.
Why Solid Modelling?

11. Geometric Modelling
X= r sinθ,
Y= r cosθ
and Z= h
When we give some values to
these 3 variables, ie.
r=10, θ= Π and h=25
It would be a point (X,Y,Z).
X= r sinθ,
Y= r cosθ
and Z= h
But when we vary one
parameter say θ then, ie.
r=10, -Π≤θ≤Π and h=25
It would be a circle.
X= r sinθ,
Y= r cosθ
and Z= h
But when I vary one more
parameter say θ and h then, ie.
r=10, -Π≤θ≤Π and 0≤h≤25
It would be a cylinder.
Let us see one example…
What do these equations represents

12. Geometric Modelling
X= r sinθ,
Y= r cosθ
and Z= h
If I vary r and θ keeping
h=const., ie.
0≤r≤10, -Π≤θ≤Π and h=25
It would be a disk.
X= r sinθ,
Y= r cosθ
and Z= h
If I vary all three r, θ and h, ie.
0≤r≤10, -Π≤θ≤Π and 0≤h≤25
It would be a Solid Cylinder.
X= r sinθ,
Y= r cosθ
and Z= h
If I vary all three r, θ and h, ie.
5≤r≤10, -Π≤θ≤Π and 0≤h≤25
It would be a Hollow Cylinder.

13. • Modelling Porous Medium
• Biomedical Applications
• Modelling Non-homogeneous Materials
– varying density
– changing composition
– multiple phases (solid, liquid)
New challenges to Geometric Modelling

14. Thank You…