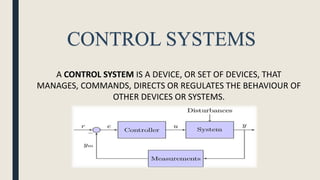
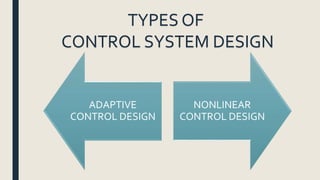
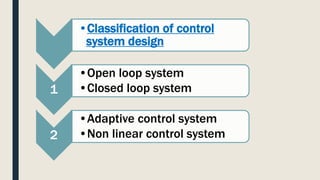
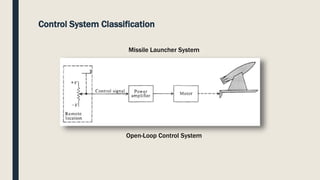
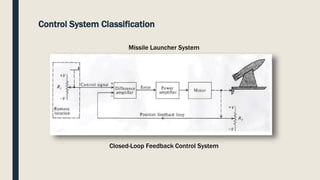
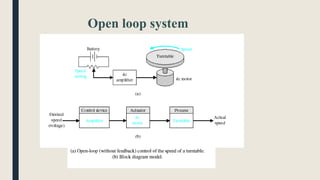
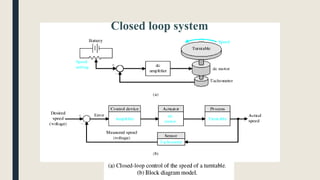
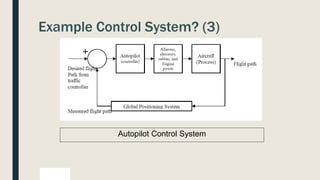
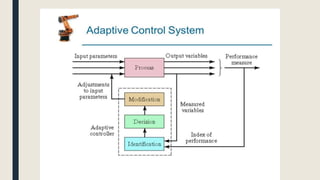
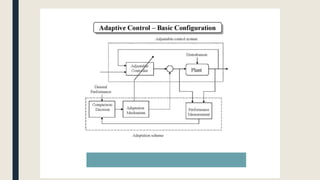
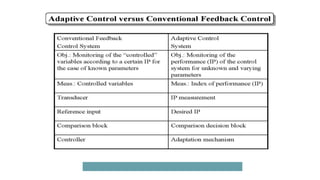
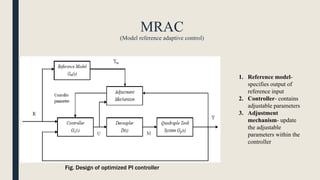
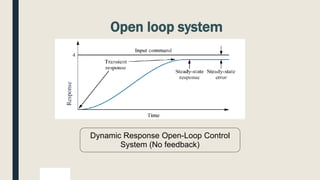
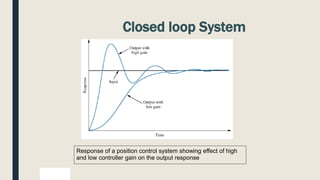
The document provides an introduction to control system design. It discusses that a control system manages the behavior of devices through feedback loops. The summary discusses the main types of control system designs: 1. Open loop and closed loop systems, with closed loop using feedback to regulate outputs based on inputs. 2. Adaptive control systems that can adapt to uncertain or changing parameters. 3. Nonlinear control systems that can handle systems with nonlinear characteristics. 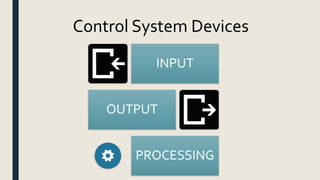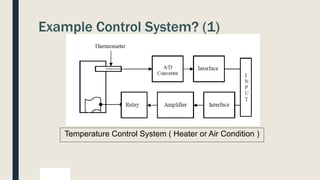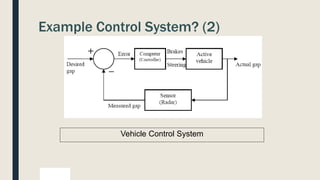The document outlines common control system components like inputs, outputs, and processing devices. It also provides examples of control systems for applications like temperature control and vehicle cruise control.

1. INTRODUCTION
TO
CONTROL SYSTEM DESIGN
PRESENTED BY:-
HITESH SHARMA
HOZEFA HUSSAIN
JAI RAWAL
JASPREET SINGH
JATIN VIJAY
JITENDRA LAKHARA
KAILASH SHARMA
KAPIL KULHAR
KARTIK KHANDELWAL
PRESENTED TO:-
MR. HIMANSHU SINGH RATHORE
DEPT. OF MECHANICAL ENGINEERING,
SKIT

2. CONTROL SYSTEMS
A CONTROL SYSTEM IS A DEVICE, OR SET OF DEVICES, THAT
MANAGES, COMMANDS, DIRECTS OR REGULATES THE BEHAVIOUR OF
OTHER DEVICES OR SYSTEMS.

3. TYPES OF CONTROL SYSTEM
OPEN LOOP
CONTROL
SYSTEM
CLOSED LOOP
CONTROL
SYSTEM

4. TYPES OF
CONTROL SYSTEM DESIGN
ADAPTIVE
CONTROL DESIGN
NONLINEAR
CONTROL DESIGN

5. Control System Devices
INPUT
OUTPUT
PROCESSING

6. INPUT CONTROL DEVICES
Input devices are used to sense a condition, detect movement or
position, indicate a limit or set point has been reached, sense
intervention by an operator, detect an alarm, etc. Typical input devices
may include limit switches, photoelectric sensors, pushbuttons,
proximity sensors, an operator interface, etc.

7. OUTPUT CONTROL DEVICES
Output devices are used to control actions such as motion, start/stop of
equipment like conveyors and pumps, on/off control of valves, operator
alerts/prompts, status indications, etc. Typical output devices include
relays, motor starters, pilot lights, operator interface graphics and numeric
display, etc.

8. PROCESSING CONTROL DEVICE
All control systems can typically be defined as having inputs, outputs and some
form of decision making going on in between so that the outputs are controlled
based on the status of the inputs. This brings us to our third category, the
"decision making" element.
The microprocessor used on the motherboard, along with its memory, the
operating system, and the application program would serve as the decision
making element. As a matter of fact, PCs are used in some automated control
systems as the decision making element, together with industrial input and
output (I/O) modules

9. Purpose of Control Systems
i. Power Amplification (Gain)
– Positioning of a large radar antenna by low-power rotation of a knob
ii. Remote Control
– Robotic arm used to pick up radioactive materials
iii. Convenience of Input Form
– Changing room temperature by thermostat position
iv. Compensation for Disturbances
– Controlling antenna position in the presence of large wind disturbance
torque

10. •Classification of control
system design
1
•Open loop system
•Closed loop system
2
•Adaptive control system
•Non linear control system

11. Control System
1. Open-loop control system – operates without the feedback loop
– Simpler and less expensive
– Risk that the actuator will not have the intended effect
2. Closed-loop (feedback) control system – a system in which the output variable is compared with an
input parameter, and any difference between the two is used to drive the output into agreement with
the input

12. Feedback
■ Feedback is a key tool that can be used to modify the behavior of a system.
■ This behavior altering effect of feedback is a key mechanism that control
engineers exploit deliberately to achieve the objective of acting on a system to
ensure that the desired performance specifications are achieved.

13. Control System Classification
Open-Loop Control System
Missile Launcher System

14. Control System Classification
Closed-Loop Feedback Control System
Missile Launcher System

15. Open loop system

16. Closed loop system

18. Open loop system
Dynamic Response Open-Loop Control
System (No feedback)

19. Closed loop System
Response of a position control system showing effect of high
and low controller gain on the output response

20. Example Control System? (1)
Temperature Control System ( Heater or Air Condition )

21. Example Control System? (2)
Vehicle Control System

22. Example Control System? (3)
Autopilot Control System

23. ADAPTIVE CONTROL
SYSTEM DESIGN

24. Adaptive control is the control method used by a controller which must adapt to a
controlled system with parameters which vary, or are initially uncertain. For
example, as an aircraft flies, its mass will slowly decrease as a result of fuel
consumption; a control law is needed that adapts itself to such changing conditions. .
INTRODUCTION TO ADAPTIVE CONTROL

25. Basic concepts:
■ Why Adaptive Control?
■ dealing with complex systems that have unpredictable parameter deviations and
uncertainties
■ maintain consistent performance of a system in the presence of uncertainty and variations
in plant parameters
■ Adaptive control is superior to robust control in dealing with uncertainties in constant or
slow-varying parameter.
■ Estimate uncertain plant / controller parameters on-line, while using measured system
signals

26. Adaptive cruise control is similar to conventional cruise control in that
it maintains the vehicle's pre-set speed. However, unlike conventional
cruise control, this new system can automatically adjust speed in order
to maintain a proper distance between vehicles in the same lane. This is
achieved through a radar headway sensor, digital signal
processor and longitudinal controller. If the lead vehicle slows
down, or if another object is detected, the system sends a
signal to the engine or braking system to decelerate. Then,
when the road is clear, the system will re-accelerate the
vehicle back to the set speed.
EXAMPLE OF ADAPTIVE CONTROL IN AUTOMOBILE
ADVANTAGE
1.Provide relief to the driver in heavy traffic situations.
2.Improve safety of vechile and driver.
LIMITATIONS:
1.Very expansive system so used in expansive cars ie.BMW,AUDI.

31. NON LINEAR ADAPTIVE CONTROL
SYSTEM

32. Contents
■ Introduction
■ MRAC system
■ Conditions
■ Design of nonlinear control system
■ Mathematical calculations

33. Introduction
■ Principle of homogeneity or Superposition principle
■ Example: Thermostat-controlled heating system

34. MRAC
(Model reference adaptive control)
Fig. Design of optimized PI controller
1. Reference model-
specifies output of
reference input
2. Controller- contains
adjustable parameters
3. Adjustment
mechanism- update
the adjustable
parameters within the
controller

35. Conditions
■ The unknown parameters with in the nonlinear plant are linearly parameterized
■ The complete state vector is measured
■ When the unknown parameters are assumed known, the control input can cancel all the
non linarites in a feedback linearization sense and any remaining internal dynamics
should be stable.
■ Solve by MRAC method.

36. Design Of Non Linear Adaptive Control
System
1. Sketch the System layout.
2. Calculate output for reference input.
3. Compare the this output with reference
output and find error.
4. And applies this error signal to the
system to bring the output closer to the
reference.

37. Mathematical Techniques To Solve Non Linear
System
1. Limit cycle theory
2. Poincaré maps
3. Lyapunov stability theory
4. Describing functions.

38. Lyapunov Stability Theory
Lyapunov functions are scalar functions that are used to
prove the stability of an equilibrium of a Differential
Equation.
Informally, a Lyapunov function is a function that takes
positive values everywhere and decreases (or is non-
increasing) along every trajectory of the Differential
Equation.

39. Mathematical Definition Of A Lyapunov Function
Let
V : Rn
Be a continuous scalar function.
then
V is a lyapunov function if it’s a locally positive-definite function i.e.
V(0)=0
V(x)>0 where x is real number
R

40. Definition Of The Equilibrium Point Of A
System
let
y: Rn
ġ=y(g)
Value of g at which function ġ becomes zero is called equilibrium point
R

41. Basic Lyapunov Theorems For Systems

42. Basic Lyapunov Theorems For
Systems(Contd.)
■ If the Lyapunov-candidate-function V is locally positive definite and the time derivative
of the Lyapunov-candidate-function is locally negative semi definite then the
equilibrium is proven to be stable.
■ If the Lyapunov-candidate-function V is locally positive definite and the time derivative
of the Lyapunov-candidate-function is locally negative definite then the equilibrium is
proven to be locally asymptotically stable.
■ If the Lyapunov-candidate-function V is globally positive definite, radially
unbounded and the time derivative of the Lyapunov-candidate-function is globally
negative definite then the equilibrium is proven to be globally asymptotically stable.

43. Applications of control system design
■ Rotary indexer
Application type: indexing conveyor
Motion: rotary
■ Labelling machine
Application type: following
Motion: linear
■ Surface grinding machine
Application type: tool feed
Motion: Linear

44. Thank you