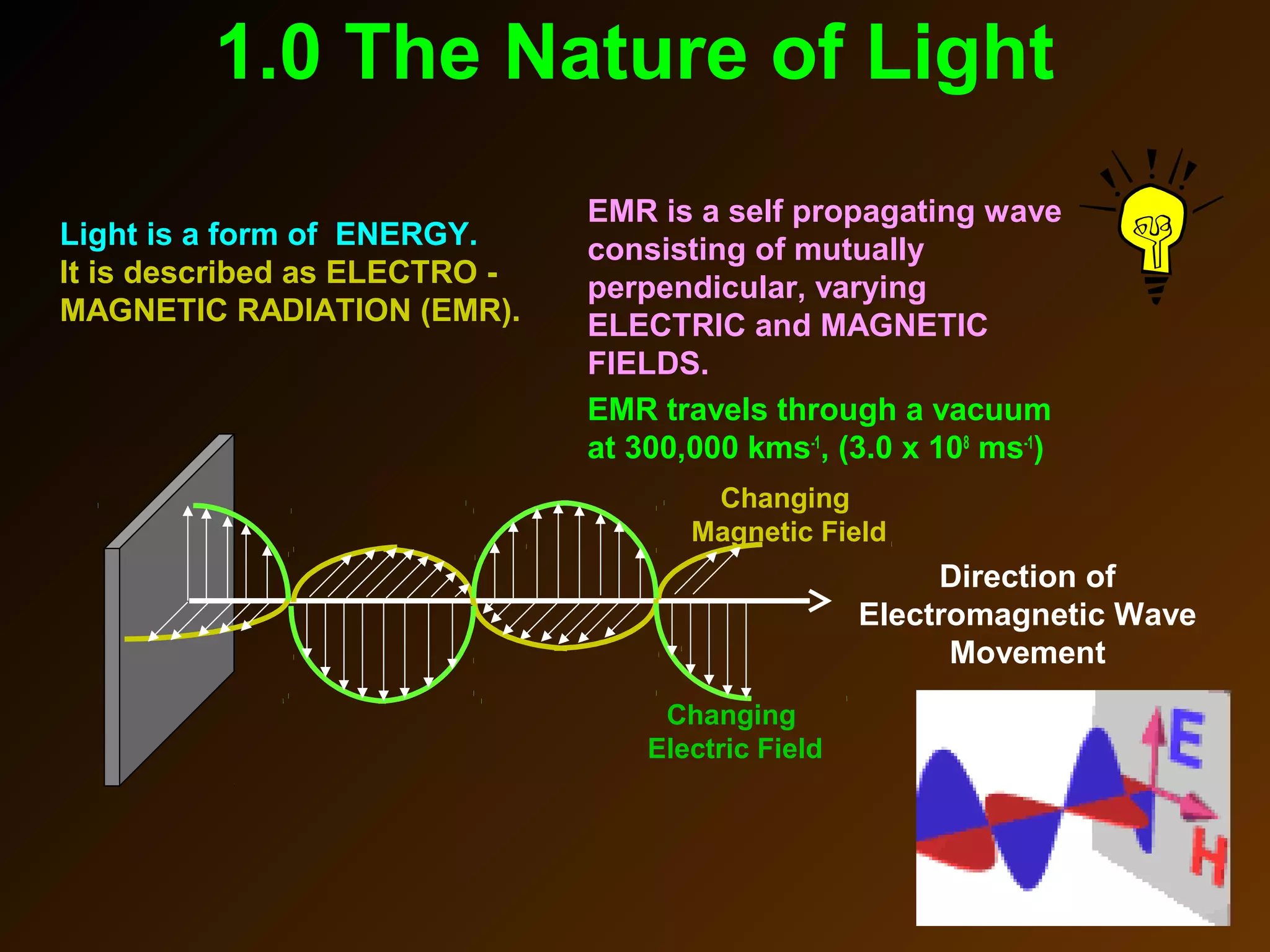
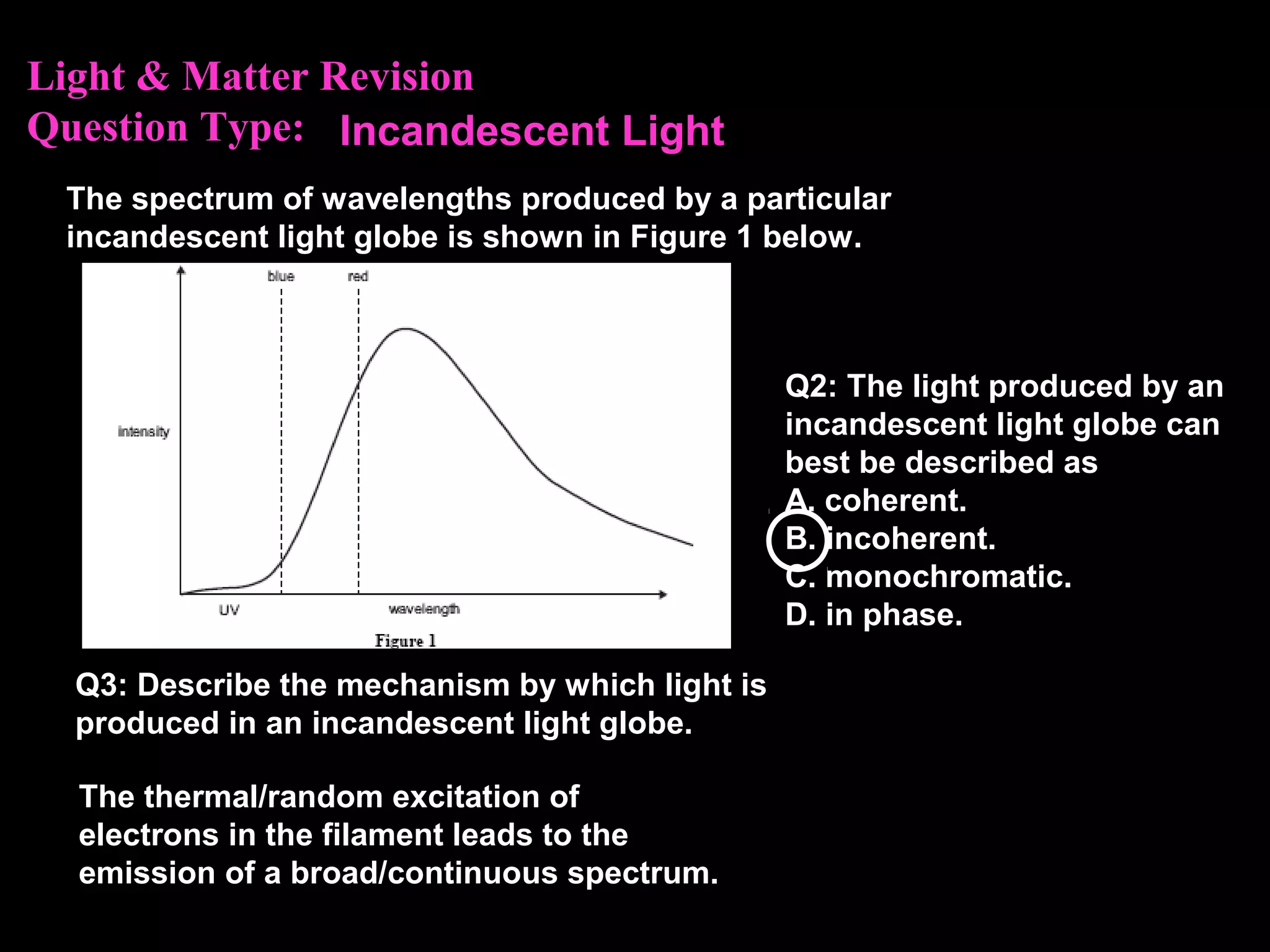
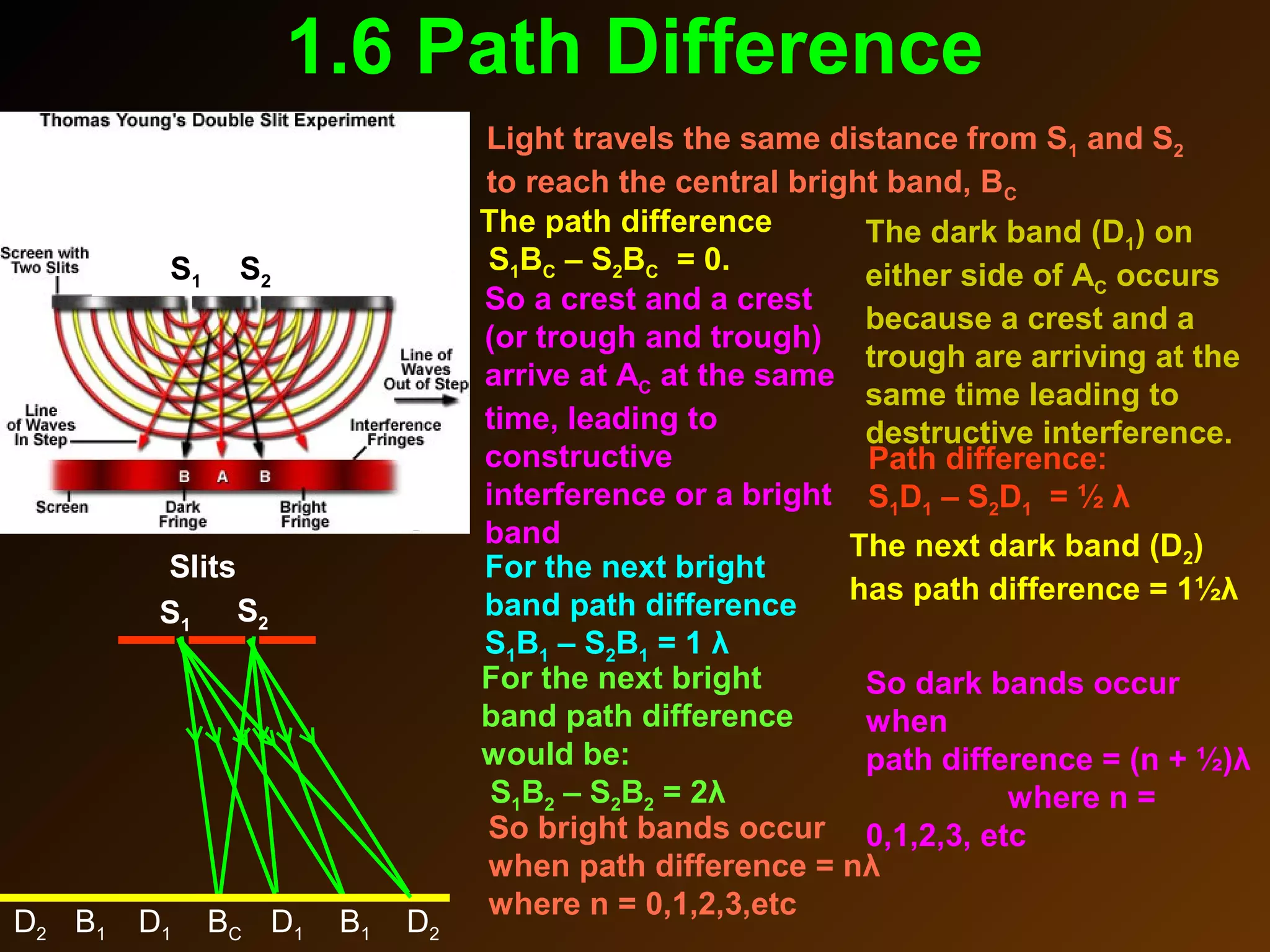
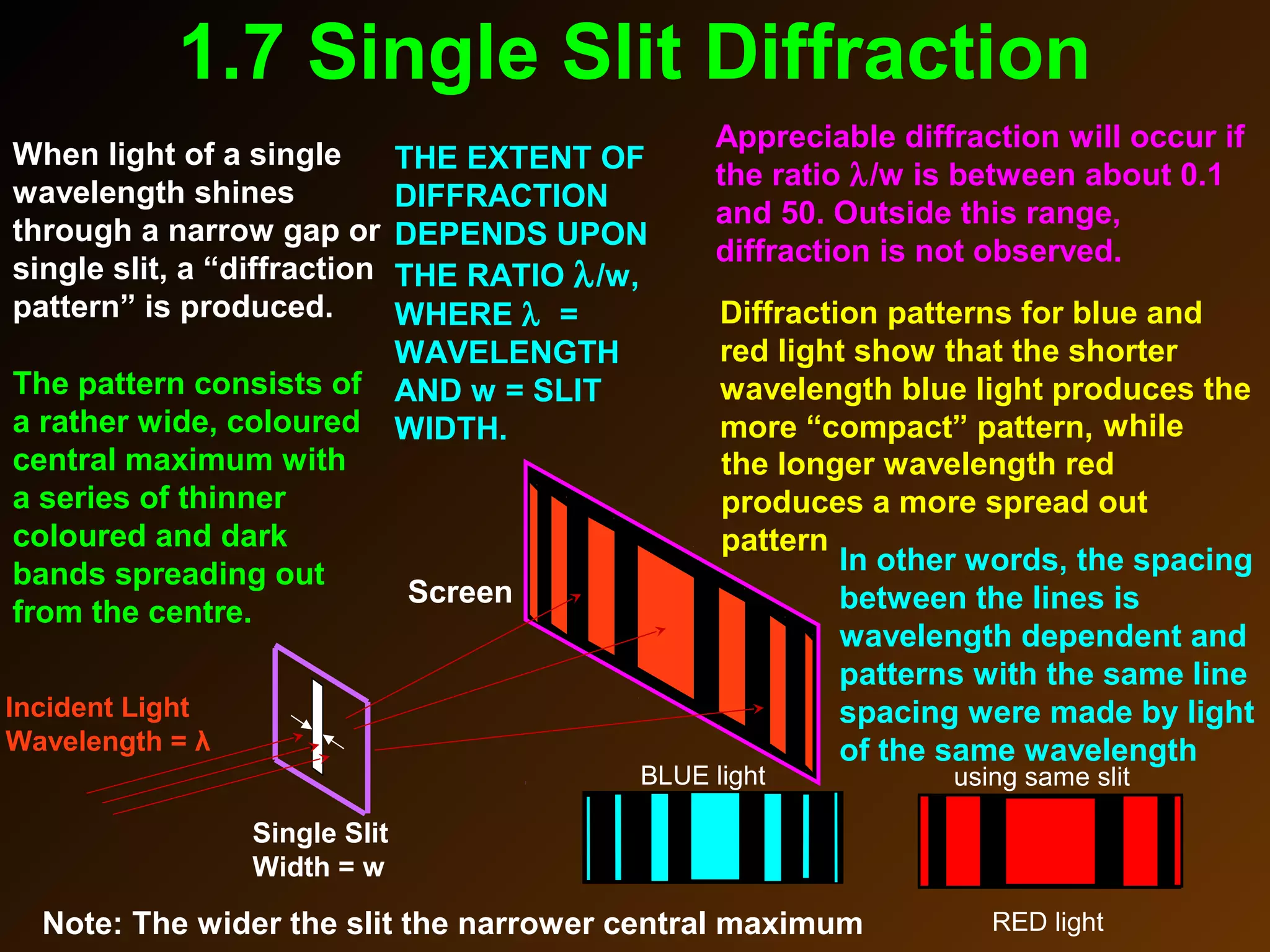
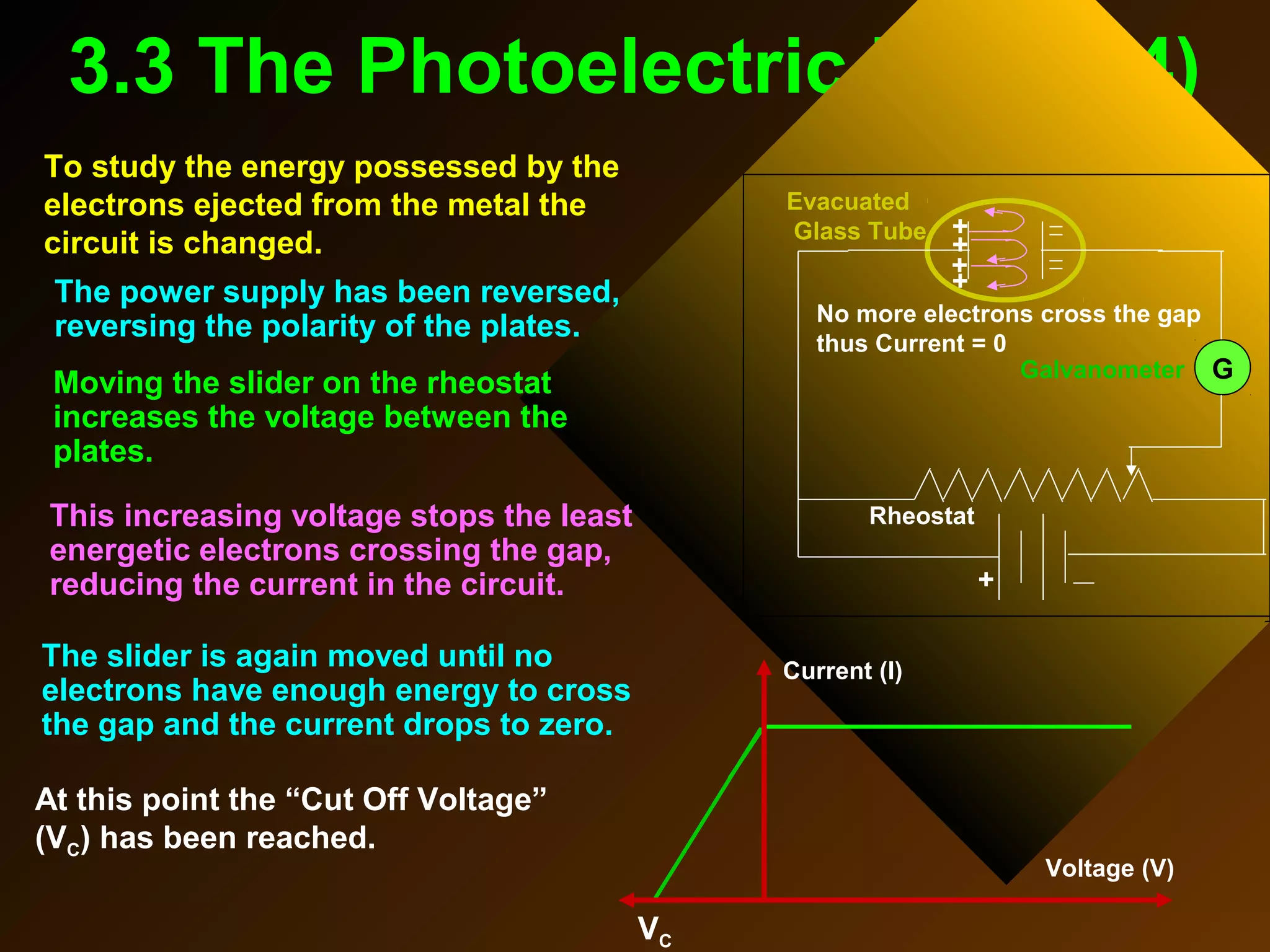
The photoelectric effect provides evidence that light behaves as particles. When light shines on a metal surface, electrons can be emitted. This is explained by assuming that light is made up of particles called photons, with each photon having an energy determined by its frequency. The kinetic energy of the emitted electrons depends on the frequency of the incident light, not its intensity. This is consistent with a particle model where each photon transfers its energy to an electron. The wave-particle duality of light is evidenced by both its particle-like properties in the photoelectric effect and its wave-like properties demonstrated in phenomena such as interference and diffraction.