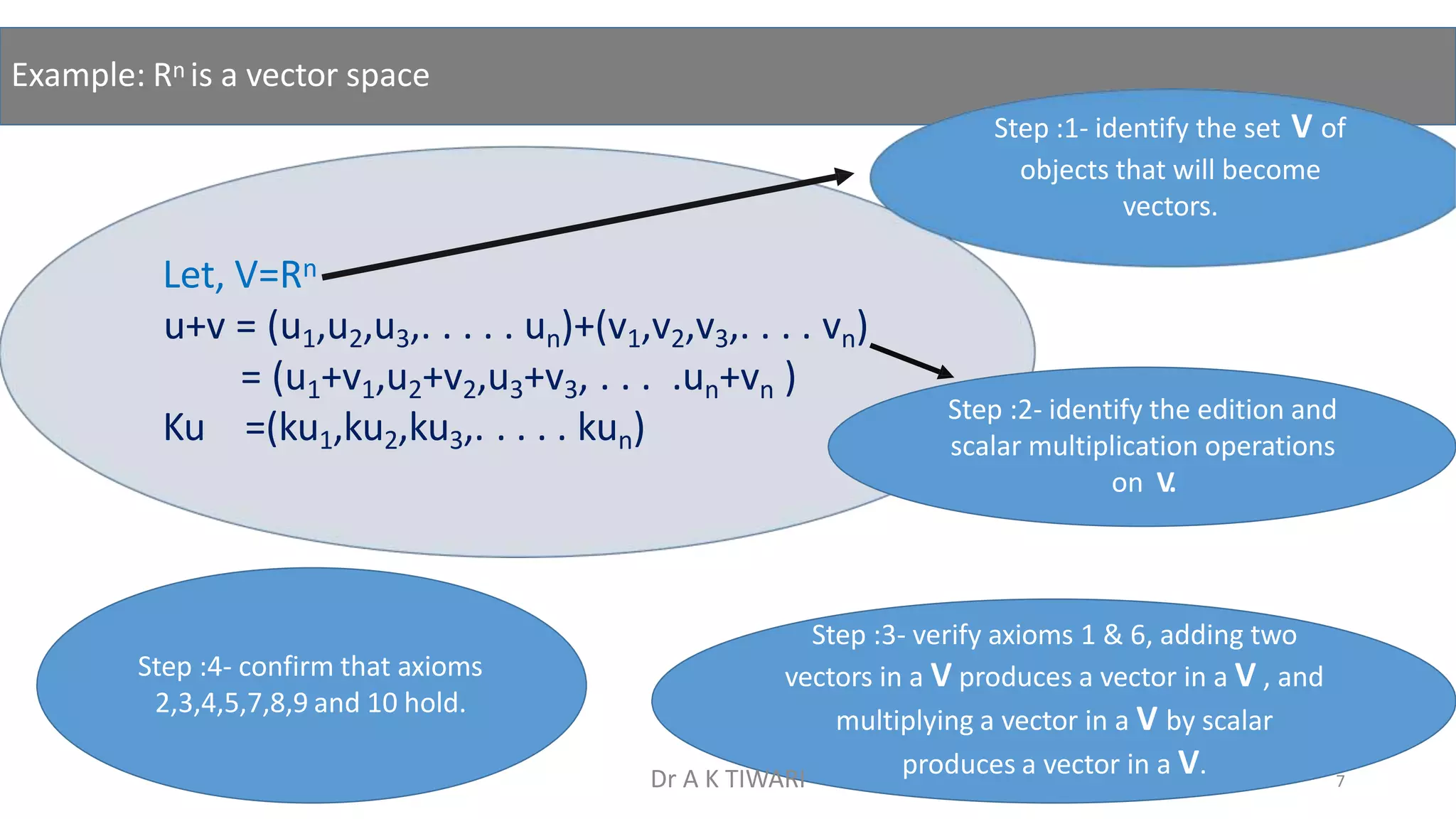
The document discusses vector spaces and related concepts. It begins by defining a vector space as a non-empty set V with defined operations of vector addition and scalar multiplication that satisfy certain axioms. Examples of vector spaces include Rn and the set of m×n matrices. A subspace is a subset of a vector space that is also a vector space under the defined operations. Properties of subspaces and examples are provided. Linear combinations, linear independence, spanning sets, and the span of a set of vectors are then defined and explained.




























![
m
mn
A
A
a
A
⁝
a
⁝
⁝
a
⁝
m2
a a 2
A1
m1
2n
21 22
a1n
a11 a12
a 21 22 2n (2)
Row vectors of A
[a , a ,…, a ] A
11 12 1n (1)
[a , a ,…, a ] A
⁝
[a , a ,…, a ] A
m1 m2 mn (n)
Column vectors of A
Row Vectors:
1 2 n
A ⁝A ⁝ ⁝A
a a
⁝
am2
2n
22
21
⁝
amn
a1n
⁝
am1
a11 a12
a
A
mn
a a a
⁝ ⁝ ⁝
m1 m2
a a a
21 22 2n
a11 a12 a1n
Column Vectors:
|| ||
A
(1)
A
(2)
||
A
(n)
Dr A K TIWARI](https://image.slidesharecdn.com/vectorspace-230520021922-e87be485/75/Vector-Space-pptx-33-2048.jpg)










![Find the coordinate matrix of x=(1, 2, –1) in R3 relative to the (nonstandard) basis
B ' = {u1, u2, u3}={(1, 0, 1), (0, – 1, 2), (2, 3, – 5)}
Sol:
x c u c u c u (1, 2, 1) c (1, 0,1) c (0, 1, 2) c (2, 3, 5)
1 1 2 2 3 3 1 2 3
1
0
1
3
2
0
1
5c 1
3c 2
2c 1
3
2
1
c 2c 5c 1
0 2 1 1 0 0 5
1 3 2 G.J
.E.
0 1 0 8
2 5 1 0 0 1 2
c 2c 1 1 0
1 3
c 3c 2 i.e. 1
2 3
1 2
2
5
B
[ x ] 8
Finding a coordinate matrix relative to a nonstandard basis
Dr A K TIWARI](https://image.slidesharecdn.com/vectorspace-230520021922-e87be485/75/Vector-Space-pptx-44-2048.jpg)
![Change of basis problem
B B B B
1
u
u ,..., v
u , 2 n
then [v]B P[v]B
where
You were given the coordinates of a vector relative to one basis B and were asked to find
the coordinates relative to another basis B'.
Transition matrix from B' to B:
Let B {u1,u2 ,...,un} and B {u1
,u2...,un} be two bases
for a vector space V
If [v]B is the coordinate matrix of v relative to B
[v]B‘ is the coordinate matrix of v relative to B'
n
B B
P u , u ,..., u
1 B 2
is called the transition matrix from B' to B
Dr A K TIWARI](https://image.slidesharecdn.com/vectorspace-230520021922-e87be485/75/Vector-Space-pptx-45-2048.jpg)

![2
B={(–3, 2), (4,–2)} and B' ={(–1, 2), (2,–2)} are two bases for R
(a) Find the transition matrix from B' to B.
B
B'
(b) Let [v] find [v]
2
1
,
Ex : (Finding a transition matrix)
0
1 0 ⁝ 3 2
I
1 ⁝ 2 1
P
(c) Find the transition matrix from B to B' .
Sol:
2
2
2
2
3
3 4
4 ⁝
⁝
1
1 22
2
2
2
2 ⁝
⁝
B
1
3 2
P 2
(the transition matrix from B' to B)
G.J.E.
B'
(a)
Dr A K TIWARI](https://image.slidesharecdn.com/vectorspace-230520021922-e87be485/75/Vector-Space-pptx-47-2048.jpg)
![
2 12 0
3 21
1
2 B B
B
[v]
1
[v] P[v]
(b)
2
1 2 ⁝ 3 4
0 1 ⁝ 2 3
1 0 ⁝ 1 2
G.J.E.
B'
2 ⁝ 2 2
B I P
-1
3
2 (the transition matrix from B to B')
2
P1
1
Check: 2
1
3 0 I
1 2
3 2 1 2 1 0
PP 2
1
0
2
Check:
[v]
1
v (1)(3,2) (0)(4,2) (3,2)
[v]
1
v (1)(1,2) (2)(2,2) (3,2)
B
B
(c)
Dr A K TIWARI](https://image.slidesharecdn.com/vectorspace-230520021922-e87be485/75/Vector-Space-pptx-48-2048.jpg)