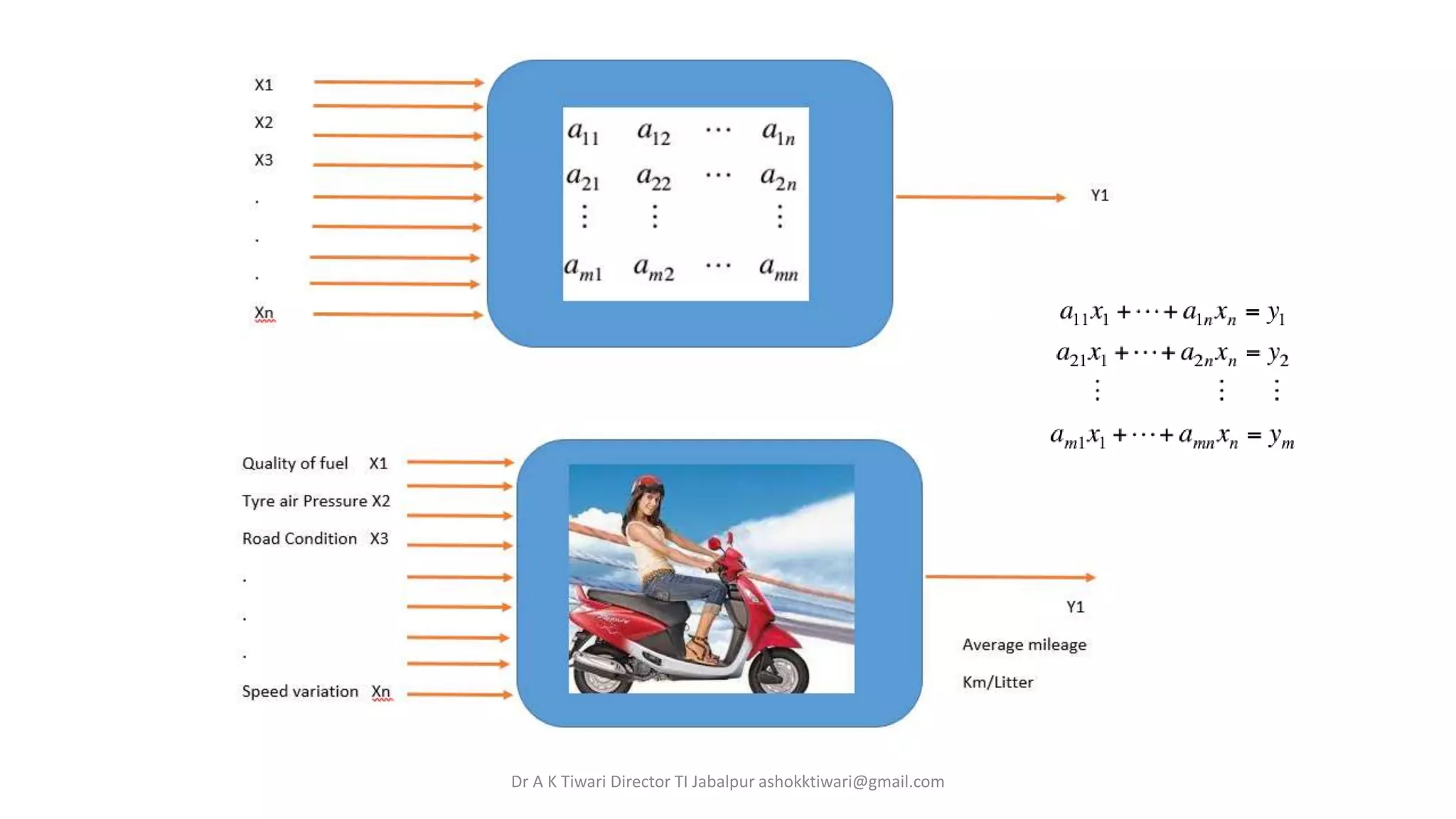
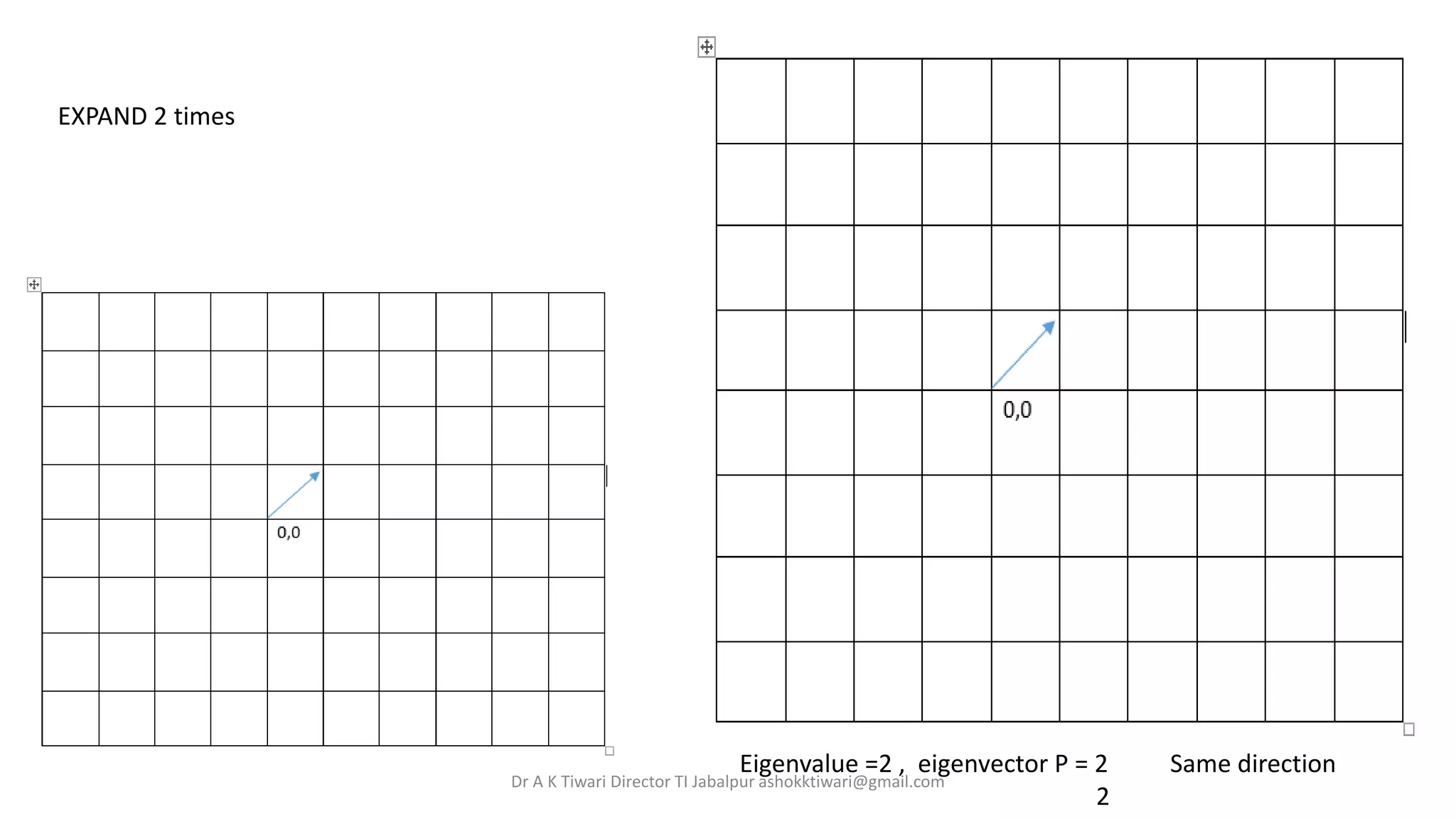
1. Linear transformations can be represented using matrices by multiplying a matrix by a vector.
2. Matrices allow linear systems of equations to be represented in a compact form known as an augmented matrix.
3. Vectors represent magnitude and direction while matrices represent linear transformations and keep track of coefficients in linear equations.