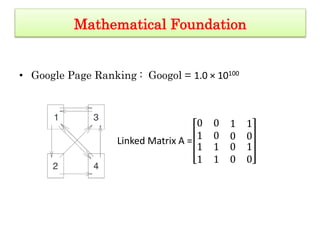
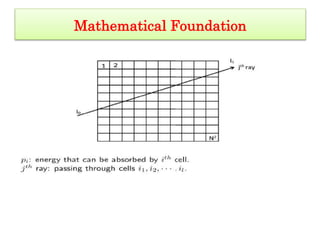
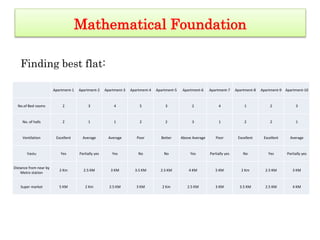
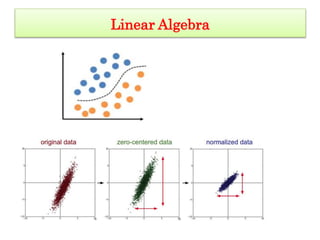
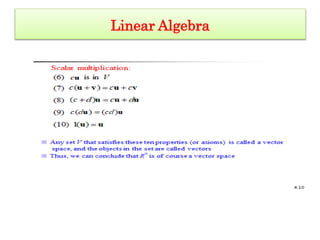
This document provides an overview of a presentation on mathematical foundations and various topics in mathematics including linear algebra, probability and statistics, calculus, and optimization. It discusses Google's PageRank algorithm and computed tomography as examples of mathematical foundations. It also provides examples of finding the best apartment based on criteria and recognizing patterns for biometric identification using machine learning models. Various concepts in linear algebra are defined such as vectors, vector spaces, subspaces, spanning sets, linear independence, basis and dimension. Examples of spanning sets, linear independence, and whether certain sets are subspaces are given. References for magnetohydrodynamic modeling of blood flow are also provided.