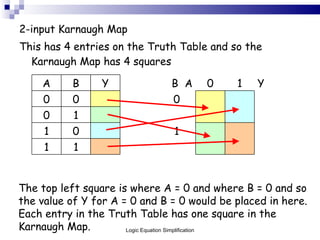
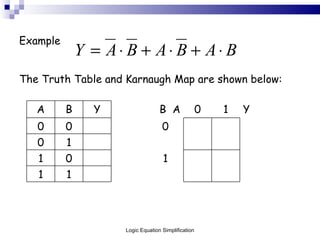
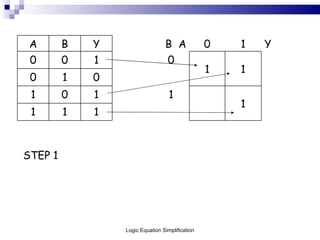
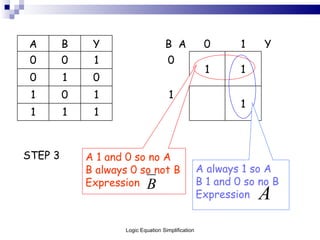
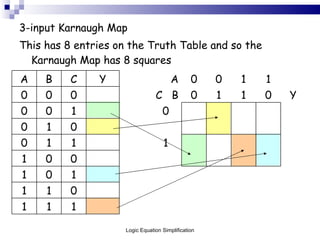
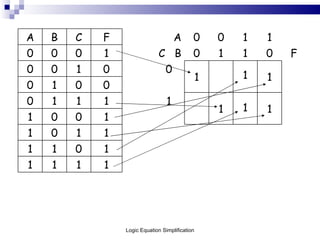
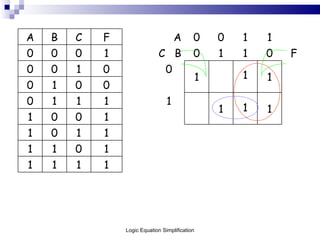
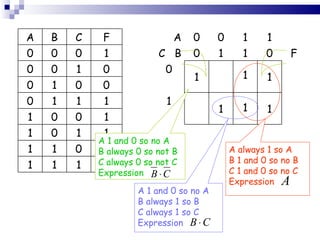
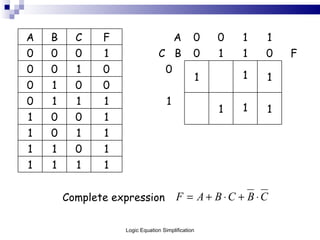
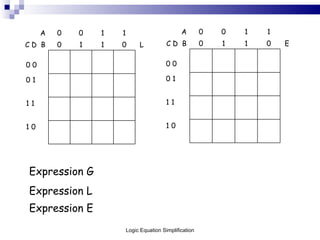
This document outlines the process of logic equation simplification, focusing on Boolean expressions and Karnaugh maps as tools for creating simpler digital logic representations. It discusses the importance of simplifying logic equations to reduce the number of gates and integrated circuits, enhancing practicality in engineering applications. The document serves as a resource for Level 4 engineering courses at the University of Wales Newport, providing methodologies, examples, and references for effective simplification techniques.

1. Logic equation simplification. Digital Logic and Software Applications © University of Wales Newport 2009 This work is licensed under a Creative Commons Attribution 2.0 License .

2. The following presentation is a part of the level 4 module -- Digital Logic and Signal Principles. This resources is a part of the 2009/2010 Engineering (foundation degree, BEng and HN) courses from University of Wales Newport (course codes H101, H691, H620, HH37 and 001H). This resource is a part of the core modules for the full time 1 st year undergraduate programme. The BEng & Foundation Degrees and HNC/D in Engineering are designed to meet the needs of employers by placing the emphasis on the theoretical, practical and vocational aspects of engineering within the workplace and beyond. Engineering is becoming more high profile, and therefore more in demand as a skill set, in today’s high-tech world. This course has been designed to provide you with knowledge, skills and practical experience encountered in everyday engineering environments. Contents Introduction Karnaugh Maps 2 Input Karnaugh Maps The Process Steps Example 3 Input Karnaugh Maps Example A function F has the truth table shown below. De... Example Three judges A, B and C vote: 1 guilty and 0 not ... Four Judge example Credits In addition to the resource below, there are supporting documents which should be used in combination with this resource. Please see: Holdsworth B, Digital Logic Design, Newnes 2002 Crisp J, Introduction to Digital Systems, Newnes 2001 Logic Equation Simplification

3. Often we are given a Boolean expression which could be written in a simplified way or we are presented with a truth table where we have no expression. The process of simplification is the way in which we generated the simplest (shortest) expression for the function. The reason that this is important is that when implementing the expression, the simpler it is the less number of gates, therefore the less number of I.C.s and the smaller the space required. e.g. Consider the OR gate truth table We have 3 combinations which generate an output: We know that this can be written as: but how do we get from the first equation to the second? A B Y 0 0 0 0 1 1 1 0 1 1 1 1

4. We will look at two methods. 1. Boolean Algebra simplification rules 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18.

5. Examples. 1. 2. Boolean Algebra requires the user to: have a good understanding of the rules, experience of reducing equations, a knowledge of where to start a knowledge of when we have reached the simplest solution. Logic Equation Simplification

6. 2. Karnaugh Maps This method coverts the truth table information into a two-dimensional map. It then converts areas of 1’s on the map into groups. These groups are then identified and this gives us the simplest expression. Logic Equation Simplification

7. 2-input Karnaugh Map This has 4 entries on the Truth Table and so the Karnaugh Map has 4 squares 1 1 1 0 1 1 0 0 0 0 Y 1 0 B A Y B A The top left square is where A = 0 and where B = 0 and so the value of Y for A = 0 and B = 0 would be placed in here. Each entry in the Truth Table has one square in the Karnaugh Map. Logic Equation Simplification

8. STEP ONE of the simplification process would be to fill in the Karnaugh Map (Note: we normally only transfer 1’s onto the map.) Logic Equation Simplification

9. STEP TWO is to group the 1’s. Groups are formed using the following rules: Group sizes must be powers of 2 – 1, 2, 4, 8, 16, etc – no other size groups are allowed. Groups must be square of rectangles (1 x 4 or 2 x 2 etc) Groups must be as large as possible (never group 2 groups of 2 if a group of 4 can be made.) All 1’s must be grouped. A 1 may be grouped more than once. Do not include redundant groups – a redundant group is a group that contains 1’s which have all been previously grouped. Logic Equation Simplification

10. STEP THREE identifies the expression for each group. The groups are examined one at a time. For a group the following question is asked for each input one at a time: For the group: Is the input logic state for every square in the group: Always 1 – if it is then the input appears in the expression Always 0 - if it is then the not input appears in the expression Both 1 and 0 - if it is then the input does not appears in the expression After each input has been checked, the expression is the AND of the inputs states identified.

11. STEP FOUR identifies the complete expression for the function. The individual group expressions are OR-ed together to give the simplified expression. Logic Equation Simplification

12. Example The Truth Table and Karnaugh Map are shown below: Logic Equation Simplification A B Y B A 0 1 Y 0 0 0 0 1 1 0 1 1 1

13. 1 1 1 1 1 0 1 0 1 0 0 1 0 0 Y 1 0 B A Y B A Logic Equation Simplification

14. 1 1 1 1 1 1 0 1 0 1 0 1 1 0 1 0 0 Y 1 0 B A Y B A STEP 1 Logic Equation Simplification

15. STEP 2 Logic Equation Simplification A B Y B A 0 1 Y 0 0 1 0 1 1 0 1 0 1 0 1 1 1 1 1 1

16. STEP 3 A always 1 so A B 1 and 0 so no B Expression A 1 and 0 so no A B always 0 so not B Expression Logic Equation Simplification A B Y B A 0 1 Y 0 0 1 0 1 1 0 1 0 1 0 1 1 1 1 1 1

17. STEP 4 Complete expression: Logic Equation Simplification A B Y B A 0 1 Y 0 0 1 0 1 1 0 1 0 1 0 1 1 1 1 1 1

18. 3-input Karnaugh Map This has 8 entries on the Truth Table and so the Karnaugh Map has 8 squares 0 1 1 1 0 1 1 1 0 1 0 0 1 1 1 1 0 0 1 0 1 0 0 Y 0 1 1 0 C B 0 0 0 1 1 0 0 A Y C B A Logic Equation Simplification

19. Note there is one additional rule for grouping 1’s on this map and larger maps: Rule: 1’s may be grouped between the left hand column and the right hand column. Logic Equation Simplification

20. Example A function F has the truth table shown below. Determine the simplest Boolean Expression for the function. Logic Equation Simplification A B C F A 0 0 1 1 0 0 0 1 C B 0 1 1 0 F 0 0 1 0 0 0 1 0 0 0 1 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 1

21. 1 1 1 1 1 0 1 1 1 1 0 1 1 0 0 1 1 1 1 1 1 1 1 0 0 0 1 0 1 1 1 0 0 1 0 0 F 0 1 1 0 C B 1 0 0 0 1 1 0 0 A F C B A Logic Equation Simplification

22. 1 1 1 1 1 0 1 1 1 1 0 1 1 0 0 1 1 1 1 1 1 1 1 0 0 0 1 0 1 1 1 0 0 1 0 0 F 0 1 1 0 C B 1 0 0 0 1 1 0 0 A F C B A Logic Equation Simplification

23. 1 1 1 1 1 0 1 1 1 1 0 1 1 0 0 1 1 1 1 1 1 1 1 0 0 0 1 0 1 1 1 0 0 1 0 0 F 0 1 1 0 C B 1 0 0 0 1 1 0 0 A F C B A A always 1 so A B 1 and 0 so no B C 1 and 0 so no C Expression A 1 and 0 so no A B always 1 so B C always 1 so C Expression A 1 and 0 so no A B always 0 so not B C always 0 so not C Expression

24. 1 1 1 1 1 0 1 1 1 1 0 1 1 0 0 1 1 1 1 1 1 1 1 0 0 0 1 0 1 1 1 0 0 1 0 0 F 0 1 1 0 C B 1 0 0 0 1 1 0 0 A F C B A Complete expression Logic Equation Simplification

25. Example Three judges A, B and C vote: 1 guilty and 0 not guilty. Design a logic circuit using NAND only which will allow a majority decision (F) to be found. e.g. A = 1, B = 0, C = 0 gives an output of 0 (not guilty) Logic Equation Simplification A B C F A 0 0 1 1 0 0 0 C B 0 1 1 0 F 0 0 1 0 0 1 0 0 1 1 1 1 0 0 1 0 1 1 1 0 1 1 1

26. 4-input Karnaugh Map This has 16 entries on the Truth Table and so the Karnaugh Map has 16 squares Logic Equation Simplification A B C D Y A 0 0 1 1 0 0 0 0 C D B 0 1 1 0 Y 0 0 0 1 0 0 0 0 1 0 0 0 1 1 0 1 0 1 0 0 0 1 0 1 1 1 0 1 1 0 0 1 1 1 1 0 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1

27. 1 1 1 1 0 1 1 1 1 0 1 1 0 0 1 1 1 1 0 1 0 1 0 1 1 0 0 1 0 0 0 1 1 0 1 1 1 0 0 1 1 0 1 1 1 0 1 0 0 0 1 0 0 1 1 1 0 0 0 1 0 0 0 0 1 0 0 0 Y 0 1 1 0 C D B 0 0 0 0 1 1 0 0 A Y D C B A Note there is one additional rule for grouping 1’s on this map and larger maps: Rule: 1’s may be grouped between the top row and the bottom row. Logic Equation Simplification

28. Example Four judges A, B, C and D vote: 1 guilty and 0 not guilty. Obtain a Boolean Expression that will allow a majority decision to be found. In the case of a split decision the vote of A determines the outcome Y. Logic Equation Simplification

29. 1 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 0 0 1 1 1 1 1 0 1 1 0 1 0 1 1 1 0 0 1 0 0 0 0 1 1 1 1 0 1 1 1 1 0 0 0 1 1 0 1 1 1 1 1 0 1 0 1 0 0 0 0 1 0 1 1 0 1 0 1 1 0 0 0 0 1 0 0 1 0 0 0 1 0 0 0 Y 0 1 1 0 C D B 0 0 0 0 0 1 1 0 0 A Y D C B A Logic Equation Simplification

30. 1 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 0 0 1 1 1 1 1 0 1 1 0 1 0 1 1 1 0 0 1 0 0 0 0 1 1 1 1 0 1 1 1 1 0 0 0 1 1 0 1 1 1 1 1 0 1 0 1 0 0 0 0 1 0 1 1 0 1 0 1 1 0 0 0 0 1 0 0 1 0 0 0 1 0 0 0 Y 0 1 1 0 C D B 0 0 0 0 0 1 1 0 0 A Y D C B A Now form groups Logic Equation Simplification

31. 1 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 0 0 1 1 1 1 1 0 1 1 0 1 0 1 1 1 0 0 1 0 0 0 0 1 1 1 1 0 1 1 1 1 0 0 0 1 1 0 1 1 1 1 1 0 1 0 1 0 0 0 0 1 0 1 1 0 1 0 1 1 0 0 0 0 1 0 0 1 0 0 0 1 0 0 0 Y 0 1 1 0 C D B 0 0 0 0 0 1 1 0 0 A Y D C B A Identify groups A always 1 so A B 1 and 0 so no B C always 1 so C D 1 and 0 so no D Expression A always 1 so A B 1 and 0 so no B C 1 and 0 so no C D always 1 so D Expression A always 1 so A B always 1 so B C 1 and 0 so no C D 1 and 0 so no D Expression A 1 and 0 so no A B always 1 so B C always 1 so C D always 1 so D Expression

32. 1 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 0 0 1 1 1 1 1 0 1 1 0 1 0 1 1 1 0 0 1 0 0 0 0 1 1 1 1 0 1 1 1 1 0 0 0 1 1 0 1 1 1 1 1 0 1 0 1 0 0 0 0 1 0 1 1 0 1 0 1 1 0 0 0 0 1 0 0 1 0 0 0 1 0 0 0 Y 0 1 1 0 C D B 0 0 0 0 0 1 1 0 0 A Y D C B A Boolean Expression Logic Equation Simplification

33. Example Two 2-bit numbers (A,B) and (C,D) are to be compared. If (A,B) > (C,D) then the G (greater than) output is to equal 1 If (A,B) < (C,D) then the L (less than) output is to equal 1 If (A,B) = (C,D) then the E (Equal to) output is to equal 1 e.g. A = 1, B = 0, C = 1, D = 1 10 (2) is less than 11 (3) so L = 1 Logic Equation Simplification

34. Logic Equation Simplification 1 1 1 1 0 1 1 1 1 0 1 1 0 0 1 1 1 1 0 1 0 1 0 1 1 0 0 1 0 0 0 1 1 0 1 1 1 0 0 1 1 0 1 1 1 0 1 0 0 0 1 0 0 1 1 1 0 0 0 1 0 0 0 0 1 0 0 0 G 0 1 1 0 C D B 0 0 0 0 1 1 0 0 A E L G D C B A

35. Expression G Expression L Expression E Logic Equation Simplification A 0 0 1 1 C D B 0 1 1 0 L 0 0 0 1 1 1 1 0 A 0 0 1 1 C D B 0 1 1 0 E 0 0 0 1 1 1 1 0

36. This resource was created by the University of Wales Newport and released as an open educational resource through the Open Engineering Resources project of the HE Academy Engineering Subject Centre. The Open Engineering Resources project was funded by HEFCE and part of the JISC/HE Academy UKOER programme. © 2009 University of Wales Newport This work is licensed under a Creative Commons Attribution 2.0 License . The JISC logo is licensed under the terms of the Creative Commons Attribution-Non-Commercial-No Derivative Works 2.0 UK: England & Wales Licence. All reproductions must comply with the terms of that licence. The HEA logo is owned by the Higher Education Academy Limited may be freely distributed and copied for educational purposes only, provided that appropriate acknowledgement is given to the Higher Education Academy as the copyright holder and original publisher. The name and logo of University of Wales Newport is a trade mark and all rights in it are reserved. The name and logo should not be reproduced without the express authorisation of the University. Logic Equation Simplification