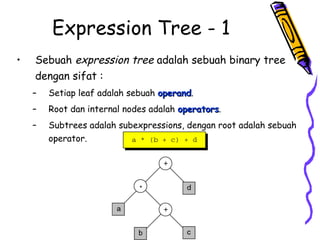
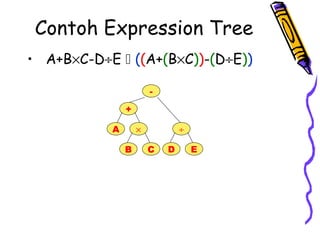
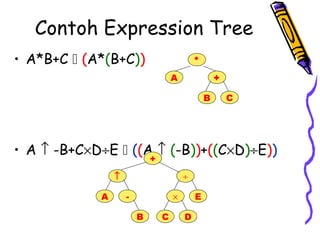
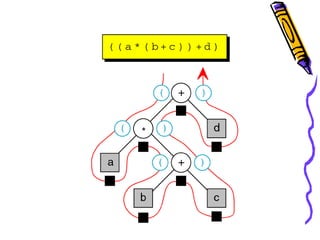
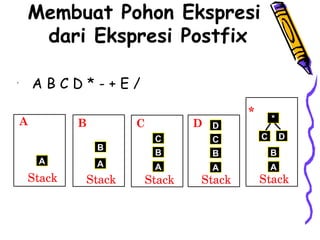
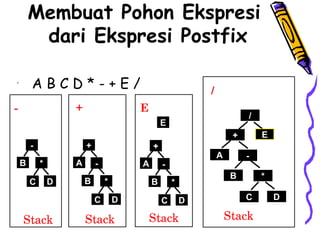
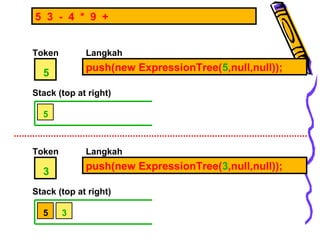
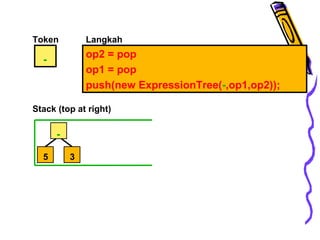
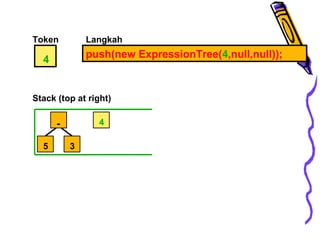
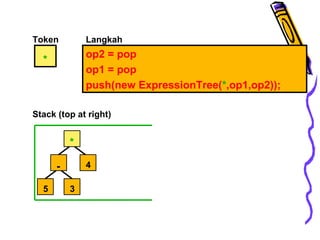
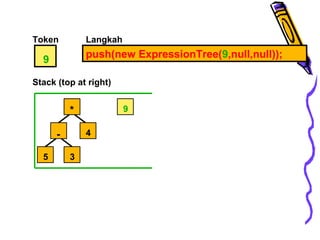
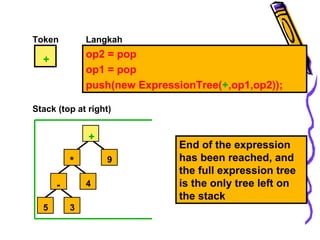
Dokumen ini membahas tentang pohon ekspresi dalam struktur data, termasuk cara membuat dan mengimplementasikan pohon ekspresi serta berbagai metode traversals (infix, postfix, prefix) yang menghasilkan format ekspresi yang berbeda. Terdapat juga penjelasan tentang konversi antara format infix, prefix, dan postfix, menggunakan stack serta pohon ekspresi. Selain itu, dokumen menyediakan contoh dan algoritma untuk membuat pohon ekspresi dari ekspresi postfix.

1. PertemuanPertemuan
Struktur DataStruktur Data
**Pohon Ekspresi *Pohon Ekspresi *
STMIK JAKARTA STI&KSTMIK JAKARTA STI&K
Disusun oleh :Disusun oleh :
Aqwam Rosadi KAqwam Rosadi K

2. 2
Kompetensi
• Mahasiswa mampu membuat dan
mengimplementasikan pohon
ekspresi
• Mahasiswa mampu mengimplementasi
pembuatan ekspresi dari pohon
ekspresi

3. Expression Tree - 1
• Sebuah expression tree adalah sebuah binary tree
dengan sifat :
– Setiap leaf adalah sebuah operandoperand.
– Root dan internal nodes adalah operatorsoperators.
– Subtrees adalah subexpressions, dengan root adalah sebuah
operator.

4. Expression Tree - 2
• Dalam expression tree, 3 cara traversals
akan membentuk 3 format ekspresi yang
berbeda yaitu : infixinfix, postfixpostfix, and prefixprefix.
– Inorder traversal menghasilkan infixinfix
expressionexpression
– Postorder traversal menghasilkan postfixpostfix
expressionexpression
– Preorder traversal menghasilkan prefixprefix
expressionexpression

5. Contoh Expression Tree
• A+B×C-D÷E  ((A+(B×C))-(D÷E))
+
A ÷
D E
-
×
B C

6. Contoh Expression Tree
• A*B+C  (A*(B+C))
• A ↑ -B+C×D÷E  ((A ↑ (-B))+((C×D)÷E))
*
A +
B C
↑
A
÷
× E
+
-
B C D

7. Infix Traversal
• Saat mencetak infix expression tree, kita
harus menambahkan kurung bukakurung buka pada awal
setiap ekspresi dan kurung tutupkurung tutup pada akhir
ekspresi.
– Dikarenakan root dari tree dan setiap
subtree dari tree menyatakan
subexpressionsubexpression, maka kita mencetak kurung
buka saat memulai sebuah tree atau
subtree dan kurung tutup saat semua anak
dari tree/subtree sudah diproses.

9. Algorithm infixinfix (val tree <tree pointer>)
if (tree not empty)
if (tree token is an operand)→
print (tree token)→
else
print (open parenthesis)
infixinfix (tree left)→
print (tree token)→
infixinfix (tree right)→
print (close parenthesis)
end if
end if
return
end infix
Infix Traversal

10. Postfix Traversal
• Menggunakan postorder traversal seperti pada tree.
• Tidak membutuhkan kurung
Algorithm postfixpostfix (val tree <tree pointer>)
if (tree not empty)
postfixpostfix (tree left)→
postfixpostfix (tree right)→
print (tree token)→
end if
return
end postfix

11. Prefix Traversal
• Menggunakan preorder traversal seperti pada tree.
• Tidak membutuhkan kurung
Algorithm prefixprefix (val tree <tree pointer>)
if (tree not empty)
print (tree token)→
prefixprefix (tree left)→
prefixprefix (tree right)→
end if
return
end prefix

12. Infix or postfix or prefix ?
• Bentuk infix 3+5*4. Berapa
hasilnya ?
• Bentuk prefix *+3 5 4. Berapa
hasilnya ?
• Bentuk 35+4*. Berapa hasilnya ?

13. Konversi bentuk infix,
prefix, postfix
• Ada 6 konversi yang dapat dikerjakan :
– infix -> prefix,
– infix -> postfix,
– prefix -> infix,
– prefix -> postfix,
– postfix -> prefix,
– postfix -> infix.
• Untuk 2 yang pertama menggunakan
stack, sedangkan 4 yang terakhir
menggunakan Expression Trees.

14. Membuat Pohon Ekspresi
dari Ekspresi Postfix
•
Menggunakan stack untuk menyimpan
operand
•
Tree yang dibuat :
–
Node yang berisi nama variabel menjadi
daun
–
Node yang berisi operator memiliki paling
sedikit 2 anak yang dapat berupa
operator lain atau node daun

15. Membuat Pohon Ekspresi
dari Ekspresi Postfix
•
A B C D * - + E /
B
B
Stack
A
A
Stack
A
B
C
Stack
A
D
Stack
C
B
A
C
D
*
Stack
B
A
C D
*

16. Membuat Pohon Ekspresi
dari Ekspresi Postfix
•
A B C D * - + E /
Stack
E
-
B
C D
-
*
Stack
+
A
B
C D
-
*
+
Stack
E
A
B
C D
-
*
+
Stack
/
/
E
A
B
C D
-
*
+

17. Membuat Pohon Ekspresi
dari Ekspresi Postfix
Ilustrasi Lain

18. 5 3 - 4 * 9 +
Token
5
push(new ExpressionTree(5,null,null));
Langkah
Stack (top at right)
5
Token
3
push(new ExpressionTree(3,null,null));
Langkah
Stack (top at right)
5 3

19. Token
-
op2 = pop
op1 = pop
push(new ExpressionTree(-,op1,op2));
Langkah
Stack (top at right)
5
-
3

20. Token
4
push(new ExpressionTree(4,null,null));
Langkah
Stack (top at right)
5
-
3
4

21. Token
*
op2 = pop
op1 = pop
push(new ExpressionTree(*,op1,op2));
Langkah
Stack (top at right)
5
-
3
4
*

22. Token
9
push(new ExpressionTree(9,null,null));
Langkah
Stack (top at right)
5
-
3
4
* 9

23. Token
+
op2 = pop
op1 = pop
push(new ExpressionTree(+,op1,op2));
Langkah
Stack (top at right)
5
-
3
4
* 9
+
End of the expression
has been reached, and
the full expression tree
is the only tree left on
the stack

24. Praktikum
• Membuat pohon ekspresi dari
ekspresi postfix
• Operasi traversal pada pohon
ekspresi
• Berupa algoritma & rancangan
program

25. “Watch your habits, for they become
your character. Develop your
character, for it becomes your
destiny”
(Perhatikan kebiasaanmu, karena itu
akan menjadi karaktermu. Bentuklah
karaktermu, karena itu akan
menentukan masa depanmu)