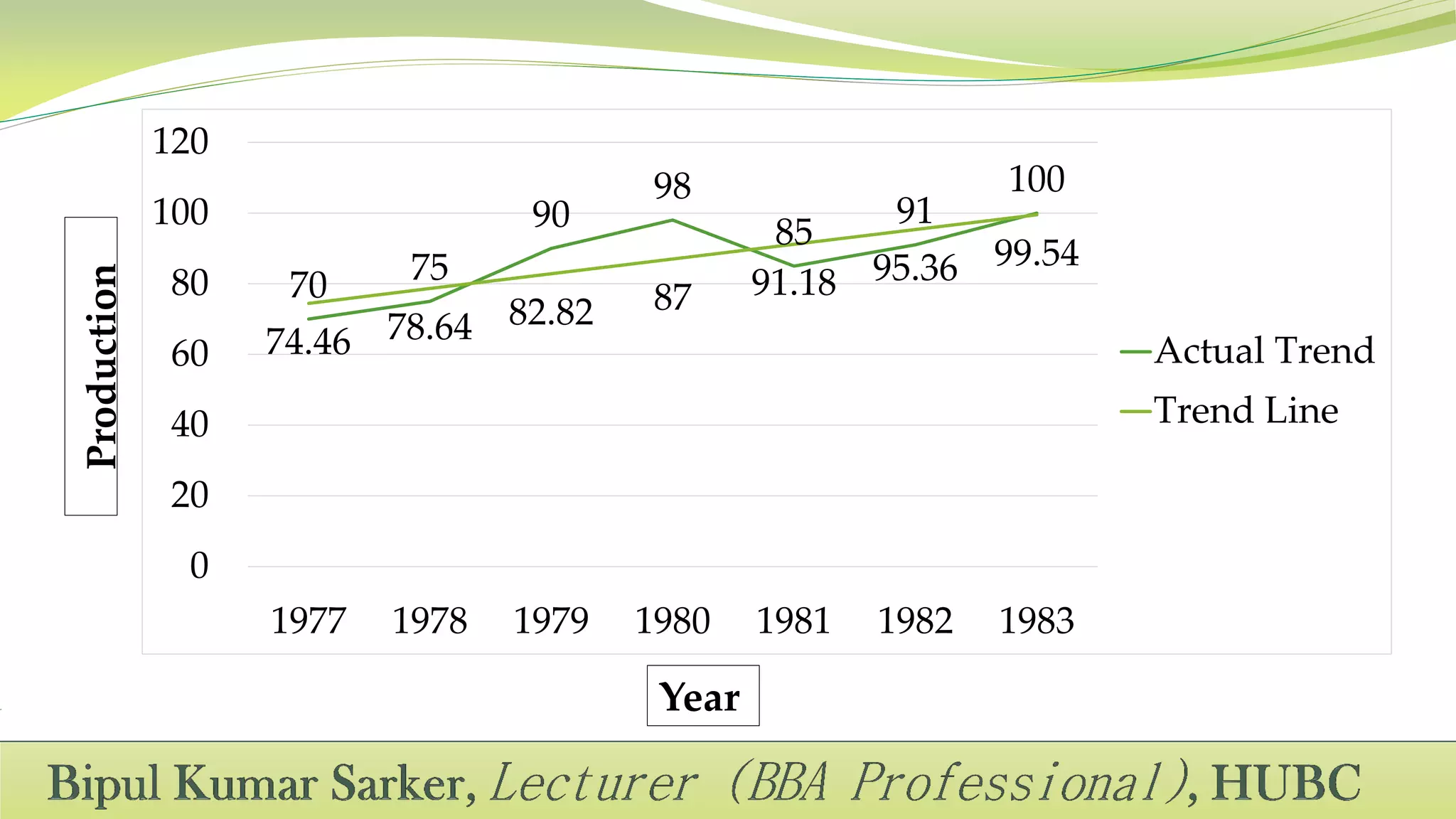
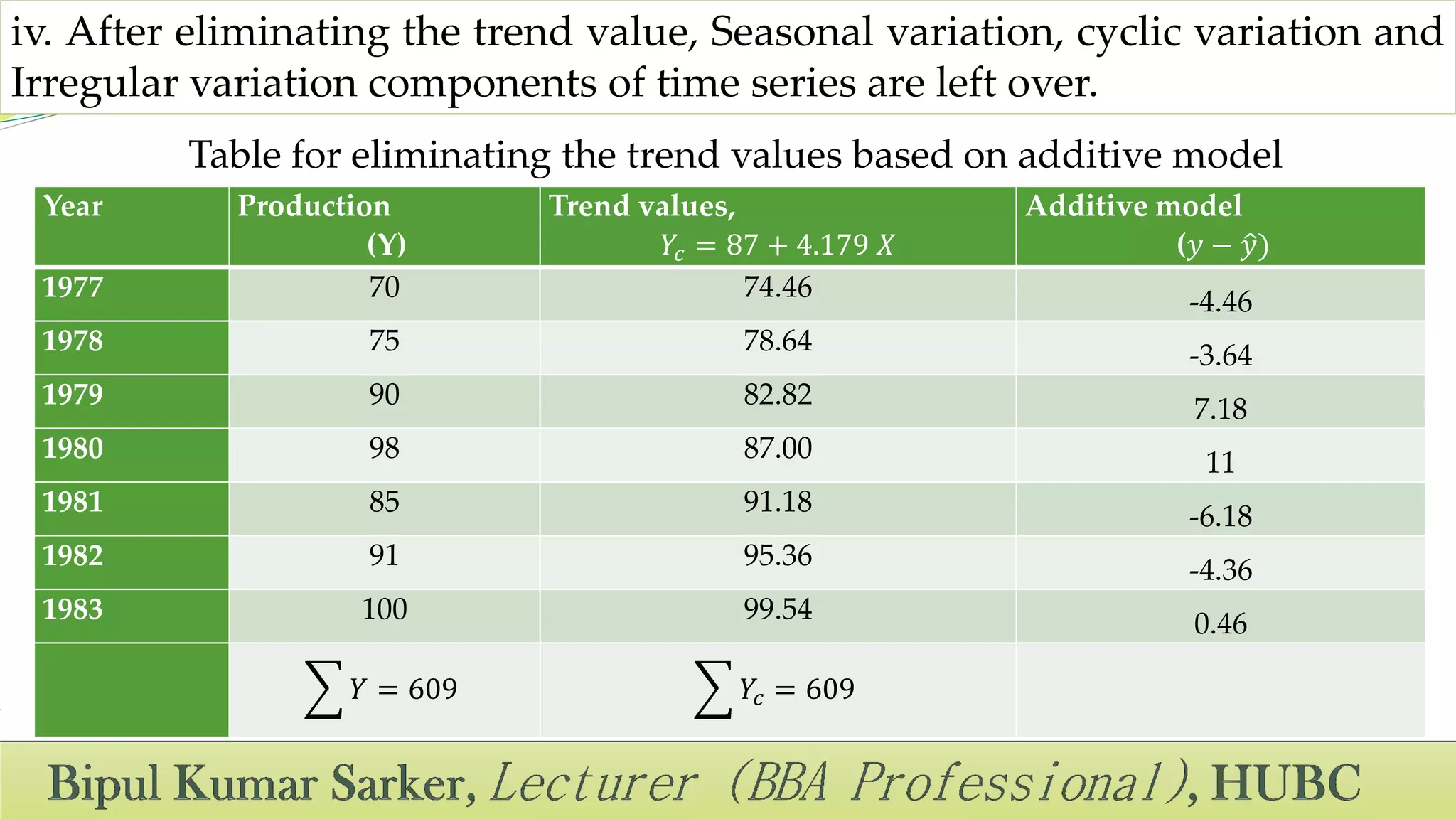
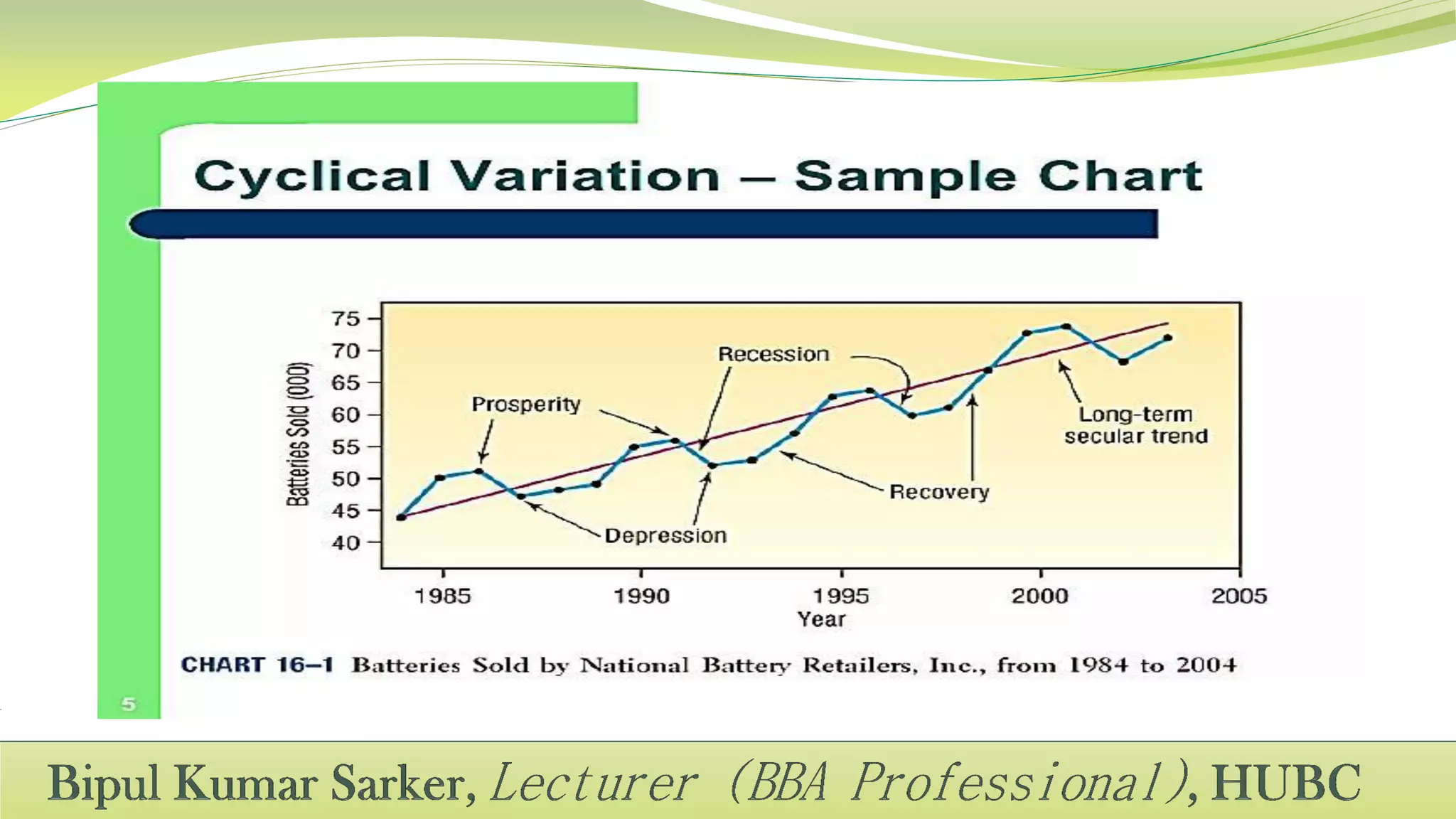
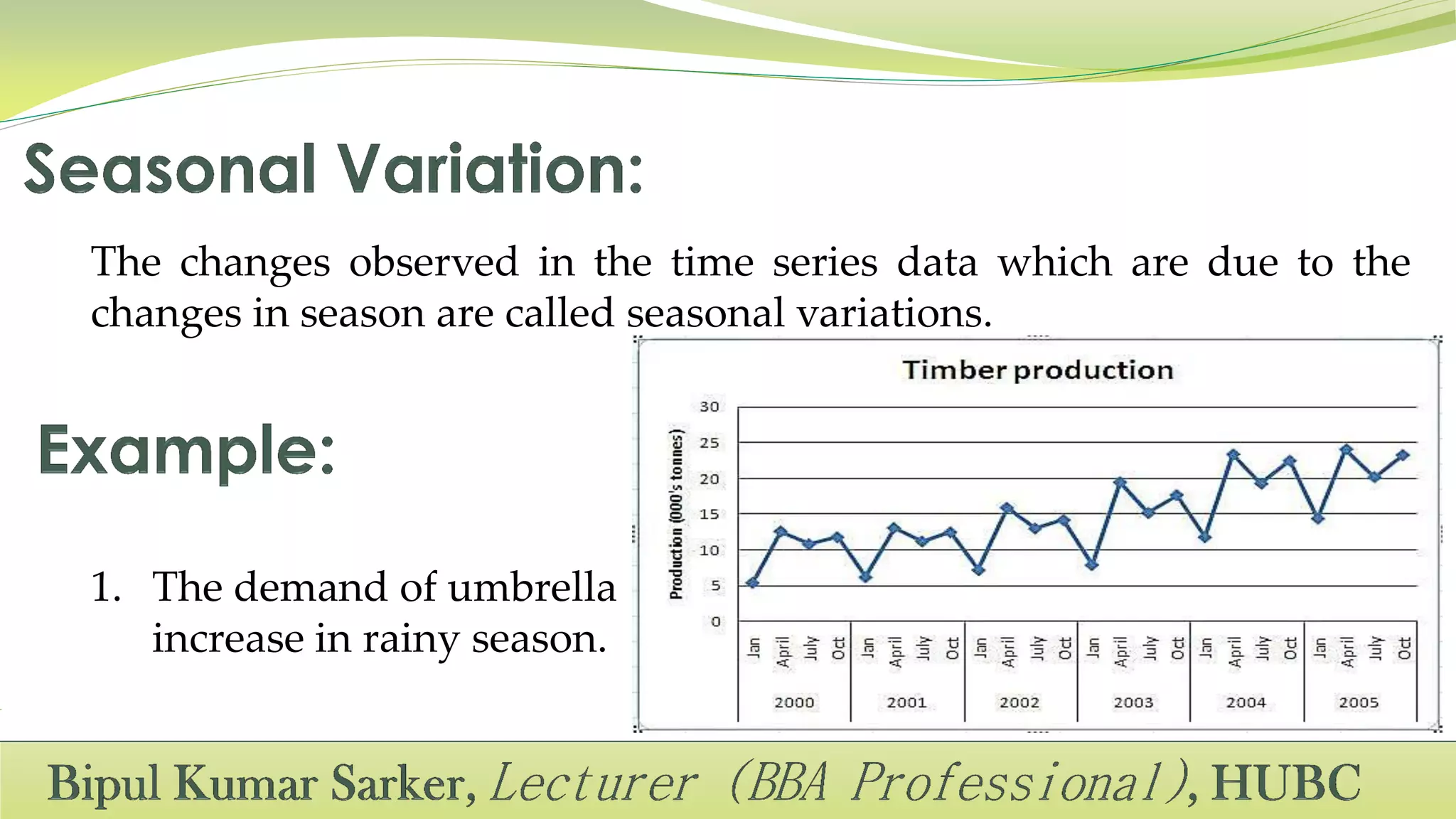
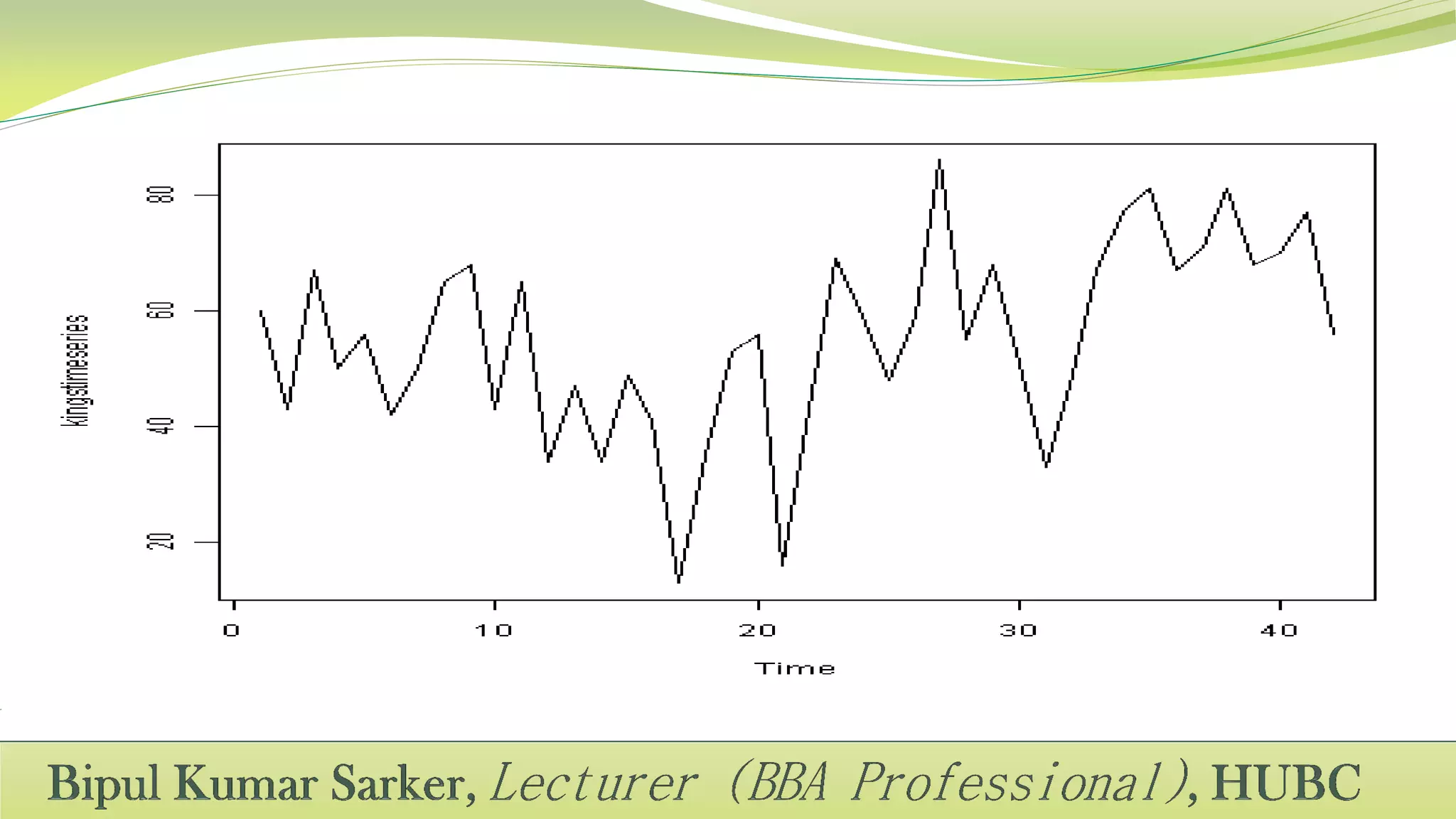
This document defines time series and its components. A time series is a set of observations recorded over successive time intervals. It has four main components: trend, seasonality, cycles, and irregular variations. Trend refers to the overall increasing or decreasing tendency over time. Seasonality refers to predictable changes that occur around the same time each year. Cycles have periods longer than a year. Irregular variations are random fluctuations. The document also discusses methods for analyzing time series components including additive, multiplicative, and mixed models.

2. A time series can be defined as ‘A set of observations of a variable recorded
at successive intervals or point of time’.
Mathematically, a time series is defined by the functional relationship
𝑌𝑡 = 𝑓 𝑡 ; 𝑡 = 𝑡1, 𝑡2, 𝑡3 … … … … … … … … … … . .
Where, 𝑌𝑡 is the value of the phenomenon at time t.

3. I. The selling amount (𝑌𝑡) of a particular Grocer’s shop in every day.
II. The no. of new born baby in Bangladesh (𝑌𝑡) in each year (t).

4. 1. Mean forecasting
2. Naïve forecasting
3. Linear trend forecasting
4. Non – Linear trend forecasting
5. Forecasting with exponential smoothing

5. 1. To study the past behavior of data.
2. To make forecasts for future.

8. 1. To study the past behavior of the phenomenon under consideration.
2. To forecast the behavior of the phenomenon in future which is
essential for future planning.
3. To compare the changes in the values of different phenomenon at
different time or places.
4. The segregation and study of the various components is of great
importance to the planner in business, policy making, decision
making and so forth.
5. To realize the actual current performance with respect to past and
future.

9. The change which are being in time, they are effected by
Economic, Social, Natural, Industrial and Political Reasons. These
reasons are called components of time series.
Components of time series:
There are four components of time series. Such as,
i. Secular Trend
ii. Seasonal Variation
iii. Cyclic variation
iv. Irregular Variation

11. The general tendency of a data set to increase or decrease or remain
stable over a period of time is called trend or secular trend or long
term movement of the data.
An upward tendency is seen in the population data while in the data
of birth, death epidemics e.t.c

12. There are two types of trend exist. Such as
I. Linear trend
II. Non-linear trend

13. If in a time series analysis, the time series values cluster more or less
around a straight line then the trend is called linear trend.
If in a time series analysis, the time series values not anyway lie
around any straight line is called the non-linear trend.

14. Cyclical variation are recurrent upward or downward movements in a
time series but the period of cycle is more than one year are called
cyclic variation.
Also these variation are not regular as seasonal variation.
The production of jute in Bangladesh which is influence by weather,
socio-economic condition, farmer’s personal view e.t.c

16. The changes observed in the time series data which are due to the
changes in season are called seasonal variations.
1. The demand of umbrella
increase in rainy season.

18. The fluctuations in a time series which are purely random,
unpredictable and are due to factors which are beyond the control of
human hands are called irregular variation.
i. Fluctuation in agricultural data due to floods, draughts e.t.c
ii. Fluctuation in the price of goods due to war.

20. Let us consider, the following components as,
𝑌𝑡 = 𝑣𝑎𝑙𝑢𝑒 𝑜𝑓 𝑡𝑖𝑚𝑒 𝑠𝑒𝑟𝑖𝑒𝑠 𝑎𝑡 𝑡𝑖𝑚𝑒 𝑡
𝑇𝑡 = 𝑇𝑟𝑒𝑛𝑑 𝑣𝑎𝑙𝑢𝑒 𝑎𝑡 𝑡𝑖𝑚𝑒 𝑡
𝑆𝑡 = 𝑠𝑒𝑎𝑠𝑜𝑛𝑎𝑙 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑜𝑛 𝑎𝑡 𝑡𝑖𝑚𝑒 𝑡
𝐶𝑡 = 𝐶𝑦𝑐𝑙𝑖𝑐 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑜𝑛 𝑎𝑡 𝑡𝑖𝑚𝑒 𝑡
𝑅𝑡 = 𝑅𝑎𝑛𝑑𝑜𝑚/𝐼𝑟𝑟𝑒𝑔𝑢𝑙𝑎𝑟 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑜𝑛 𝑎𝑡 𝑡𝑖𝑚𝑒 𝑡

21. For analysis the time series data, we have the following model:
1. Additive Model
2. Multiplicative Model
3. Mixed Model

22. We may set the additive model as,
𝒀 𝒕 = 𝑻 𝒕 + 𝑺 𝒕 + 𝑪 𝒕 + 𝑹 𝒕
Where,
𝐶𝑡 (and 𝑆𝑡 𝑖𝑓 𝑎𝑛𝑦) will have positive or negative values whether we
are in an above normal or below normal phase of the cycle and the total
of the values for any cycle would be zero.
𝑅𝑡 will also have positive or negative values and in the long run 𝑅𝑡 = 0

23. We may write the multiplicative model as
𝒀 𝒕 = 𝑻 𝒕 × 𝑺 𝒕 × 𝑪 𝒕 × 𝑹 𝒕
Where,
𝑆𝑡, 𝐶𝑡 𝑎𝑛𝑑 𝑅𝑡 are indices fluctuating above or below unity and the
geometric means of long run period are unity.

24. The mixed model can be written as
𝑌𝑡 = 𝑇𝑡 × 𝐶𝑡 + 𝑆𝑡 × 𝑅𝑡
𝑌𝑡 = 𝑇𝑡 + 𝑆𝑡 × 𝐶𝑡. 𝑅𝑡

26. 1. Graphical Method
2. Semi- Average Method
3. Moving Average Method
4. Least Square Method / Curve Fitting Method

27. Fit a Trend line to the following data, by the free-hand method.
Year 1980 1981 1982 1983 1984 1985 1986
Sales 85 110 105 110 140 180 205

28. Fitting trend line by Graphical method
Fig: Trend Line By Graphically
85
110 105 110
140
180
205
0
100
200
300
1980 1981 1982 1983 1984 1985 1986
Sales
Sales
Scale:
On the, OX- axis 5 square = 1 year
OY- axis 1 square = 10 ton

29. Fit a trend line to the following data by the method of semi-average.
Year 1992 1993 1994 1995 1996 1997 1998 1999 2000
Sales 85 110 105 110 140 180 205 82 84

30. Here, the number of years n=9 (odd) and therefore, two parts are
obtained by omitting the value corresponding to the middle time point
1996.
Table for calculation of semi-averages
Year Production (in
lac ton)
Semi-total Semi-Average
1992 60
267 66.751993 65
1994 70
1995 72
1996 73
1997 70
316 79.01998 80
1999 82
2000 84

31. Find out four year moving average from the following data:
Year 1 2 3 4 5 6 7 8 9 10 11 12
Value 53 79 76 66 69 94 105 87 79 104 98 97

32. Calculation of trend by moving- average method
Year Value 4-yearly
Moving
4- yearly moving average (centered)
1 53
2 79
3 76 68.50 70.500
4 66 72.50 74.375
5 69 76.25 79.875
6 94 83.50 86.125
7 105 88.75 90.000
8 87 91.25 92.500
9 79 93.75 92.875
10 104 92.00 93.250
11 98
12 97

33. The production of a fertilizer factory (in thousand tons) are given below:
Year 1977 1978 1979 1980 1981 1982 1983
Production 70 75 90 98 85 91 100
I. Compute the linear trend vales by the least square method and plot the value in a chart.
II. Estimate the probable production of 1985.
III. What is the monthly and quarterly fertilizer production?
IV. After eliminating the trend values what components of the time series are thus left over?
V. Eliminating the trend values based on additive model.

34. Solution:
Let us consider, time (x) = 𝑇𝑖𝑚𝑒 − 1980
And Production = Y
Year Production (Y) X = Time -
1980
XY 𝑋2
Trend values,
𝑌𝑐 = 𝑋87 + 4.179 𝑋
1977 70 -3 -210 9 74.46
1978 75 -2 -150 4 78.64
1979 90 -1 -90 1 82.82
1980 98 0 0 0 87.00
1981 85 1 85 1 91.18
1982 91 2 182 4 95.36
1983 100 3 300 9 99.54
𝑌 = 609 𝑋 = 0 𝑋𝑌 = 17 𝑋2
= 28 𝑌𝑐 = 609

35. Let the equation of the linear trend is,
𝒀 = 𝒂 + 𝒃𝑿
Where,
x denotes time
𝑌𝑐 𝑖𝑠 𝑡𝑕𝑒 𝑡𝑟𝑒𝑛𝑑 𝑣𝑎𝑙𝑢𝑒 𝑜𝑓 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒 𝑎𝑡 𝑡𝑖𝑚𝑒 𝑡
a and b are constants

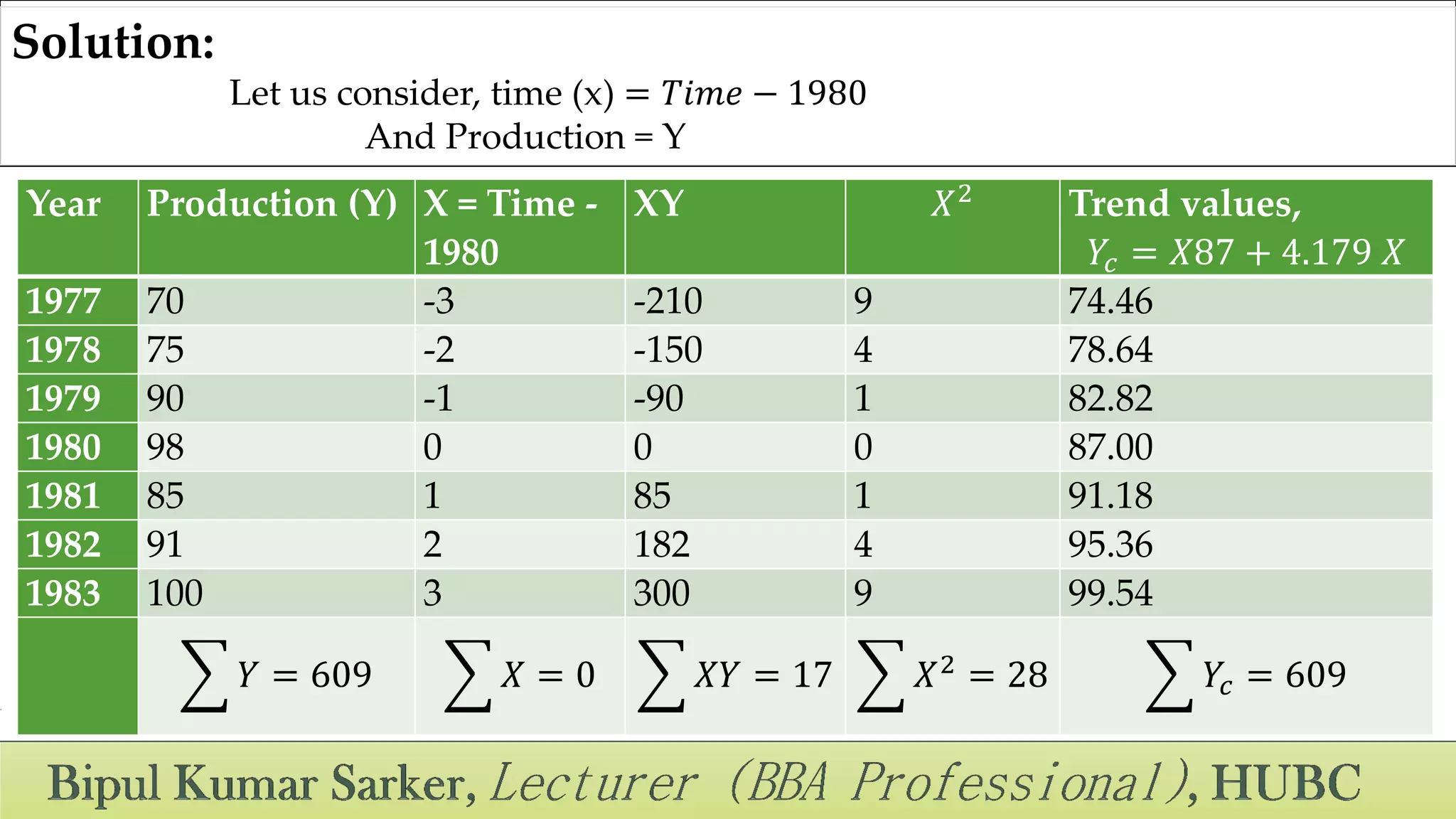
36. Here, 𝑏 =
𝑋𝑌−
𝑋 𝑌
𝑛
𝑥2−
( 𝑥)2
𝑛
=
𝑋𝑌
𝑥2 =
17
28
= 4.18
𝑎 = 𝑌 − 𝑏𝑋 = 𝑌 =
𝑌
𝑛
=
609
7
= 87
[since 𝑥 = 0 ]
[since 𝑥 = 0 ]
So the estimated equation of the linear trend is,
𝒀 𝒄 = 𝟖𝟕 + 𝟒. 𝟏𝟖 𝑿

37. 70 75
90
98
85
91
100
74.46 78.64 82.82 87 91.18 95.36 99.54
0
20
40
60
80
100
120
1977 1978 1979 1980 1981 1982 1983
Actual Trend
Trend Line
Production
Year

38. ii. Estimate the probable production in 1985,
For the year 1985, coded time, 𝑋 = 𝑌𝑒𝑎𝑟 − 1985 = 1985 − 1980 = 5
So, the estimated probable production for the year 1985 is
𝑌1985 = 87 + 4.18 × 5 = 107.895

39. iii. We have the estimated trend line equation,
𝑌 = 87 + 4.18 𝑋
The monthly increase in fertilizer production
𝑏
12
=
4.18
12
= 0.348
The quarterly increase in fertilizer production
𝑏
4
=
4.18
4
= 1.045

40. Table for eliminating the trend values based on additive model
iv. After eliminating the trend value, Seasonal variation, cyclic variation and
Irregular variation components of time series are left over.
Year Production
(Y)
Trend values,
𝑌𝑐 = 87 + 4.179 𝑋
Additive model
(𝑦 − 𝑦)
1977 70 74.46 -4.46
1978 75 78.64 -3.64
1979 90 82.82 7.18
1980 98 87.00 11
1981 85 91.18 -6.18
1982 91 95.36 -4.36
1983 100 99.54 0.46
𝑌 = 609 𝑌𝑐 = 609