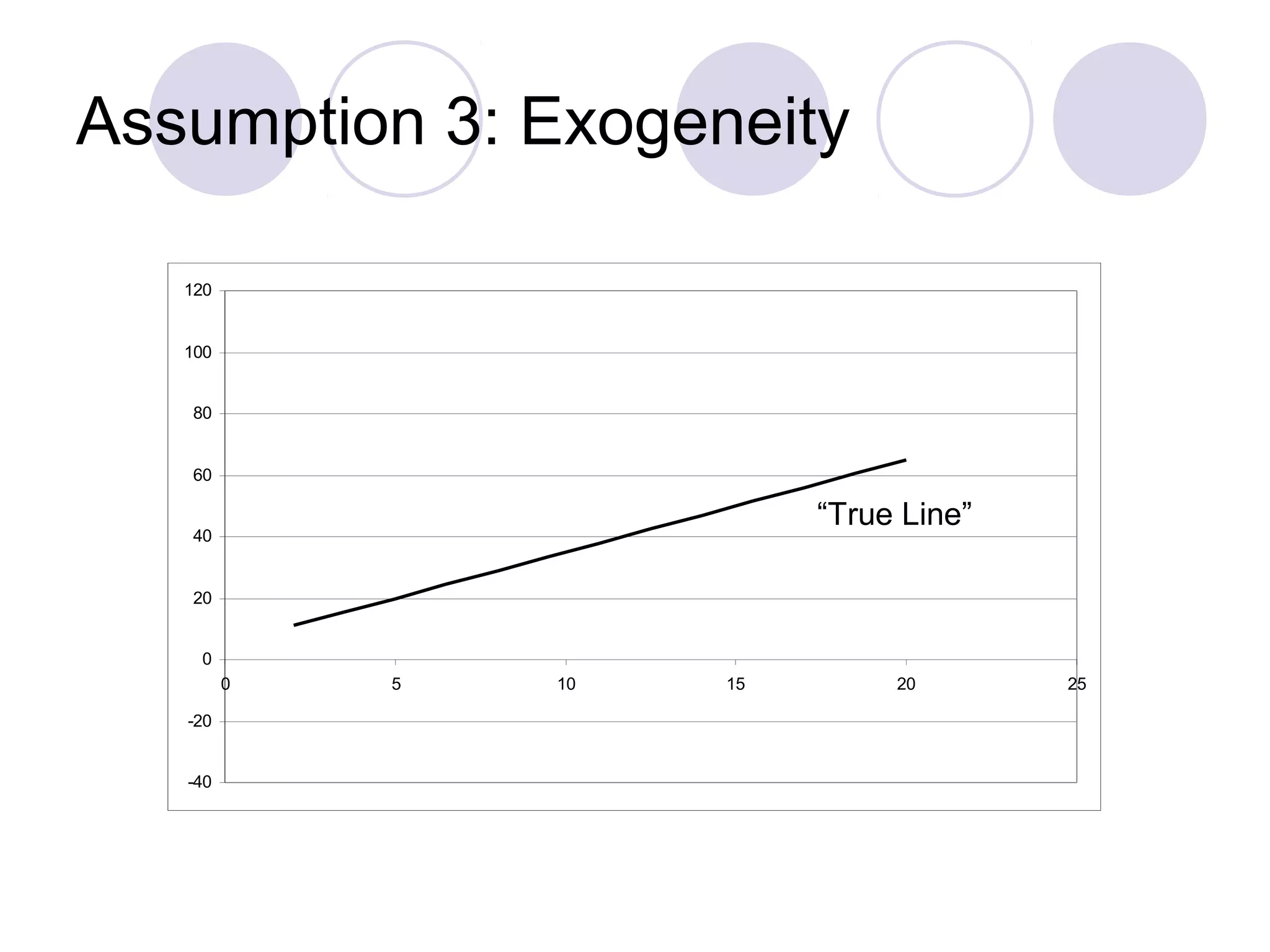
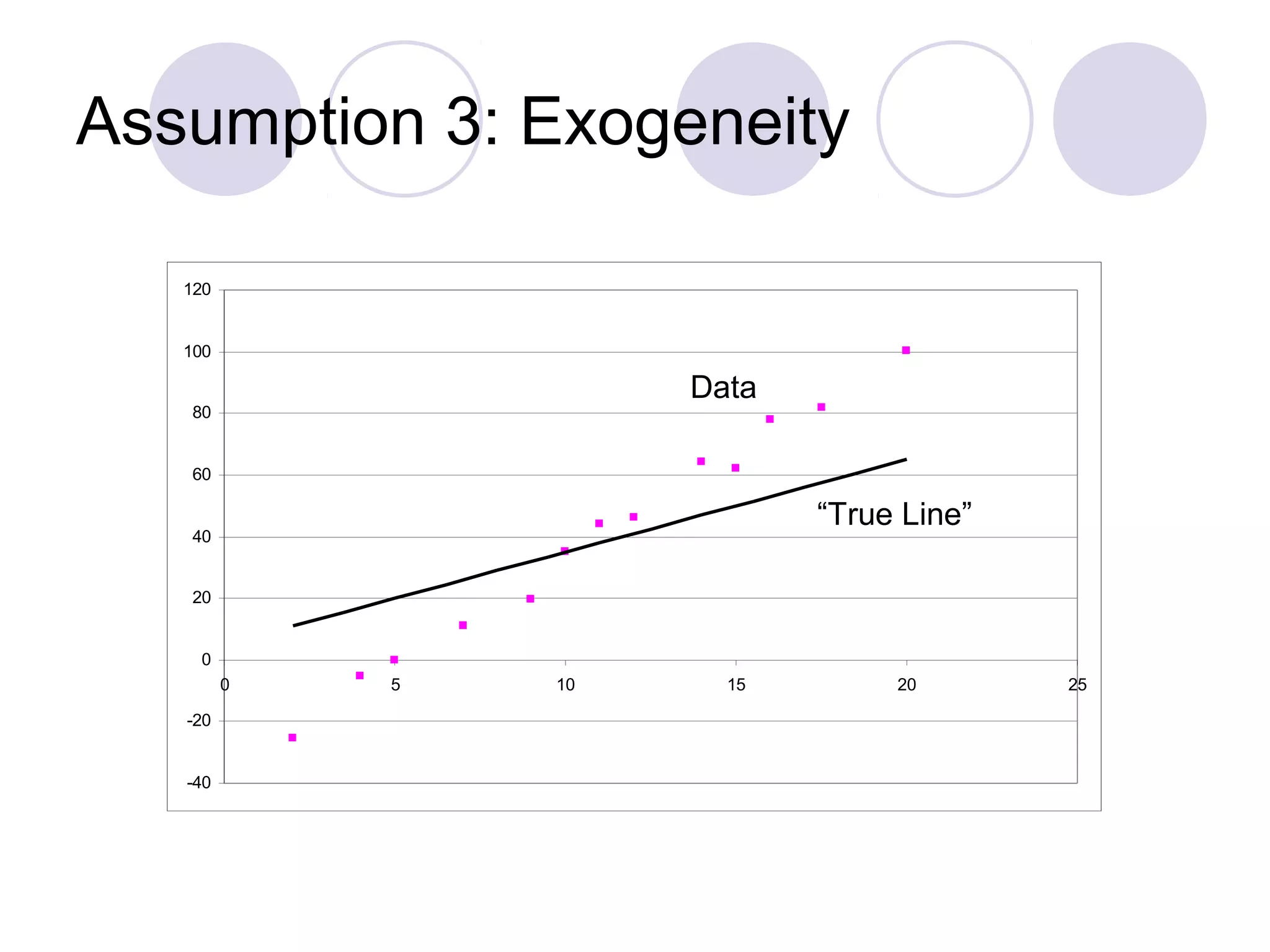
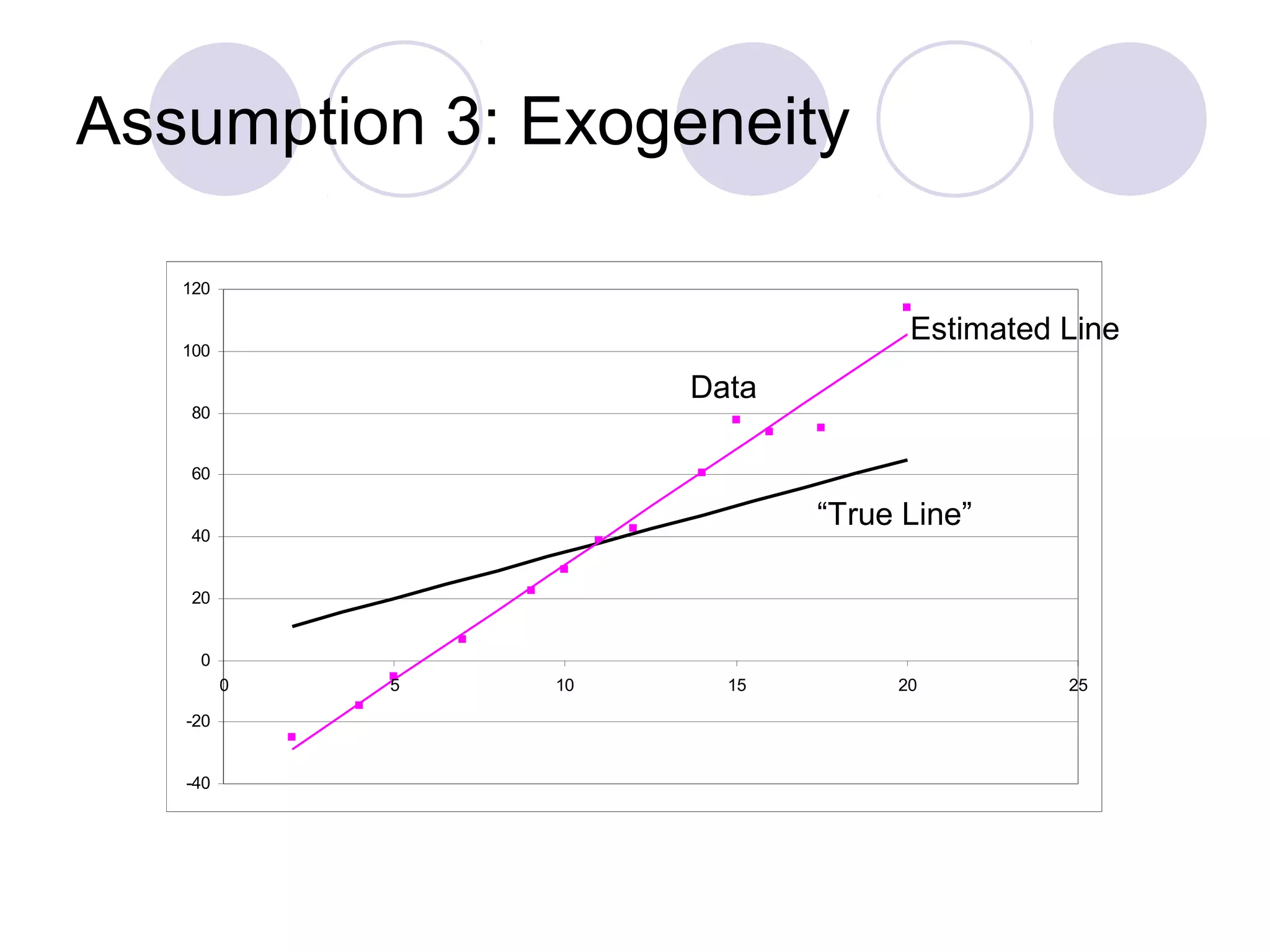
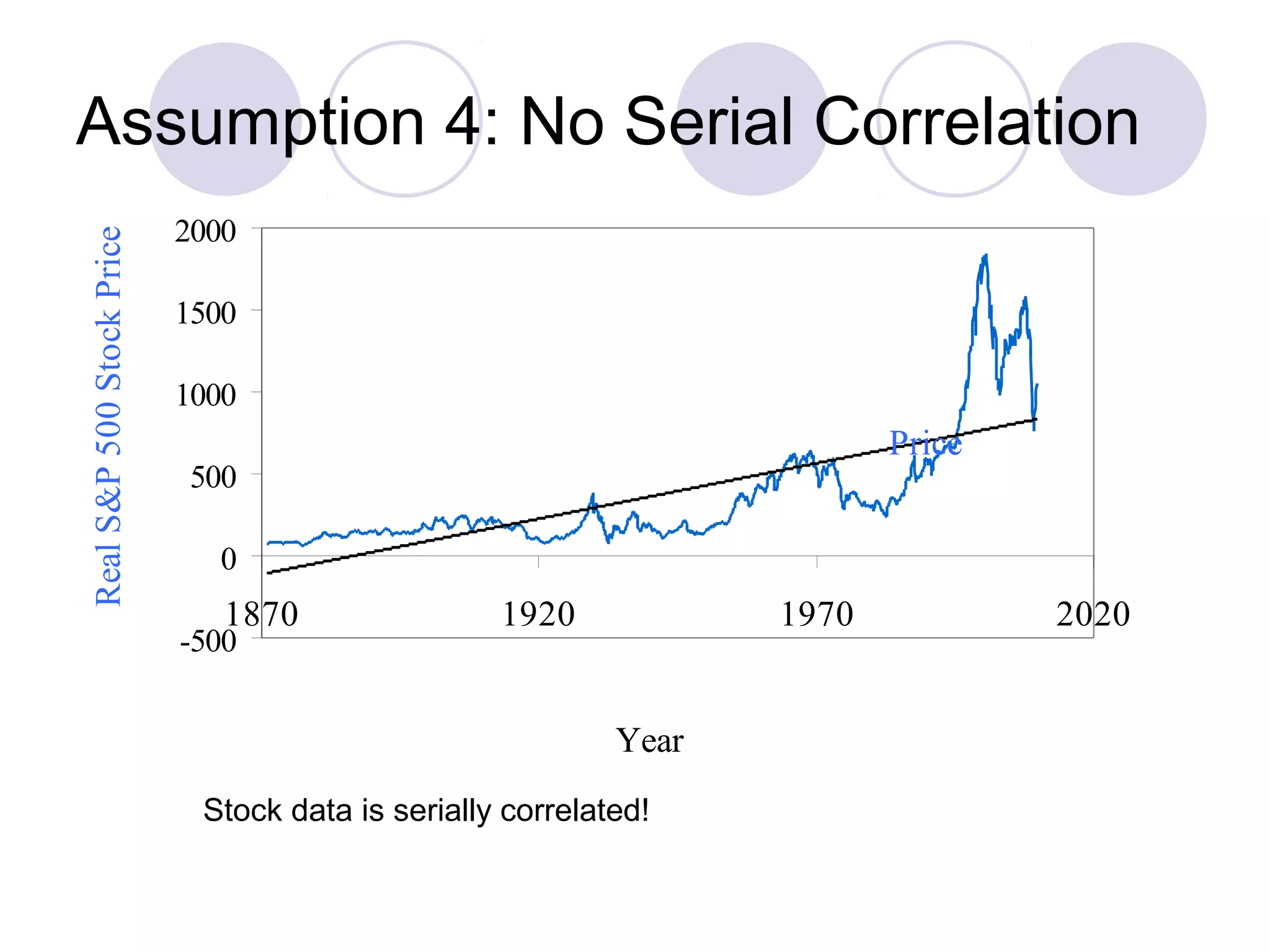
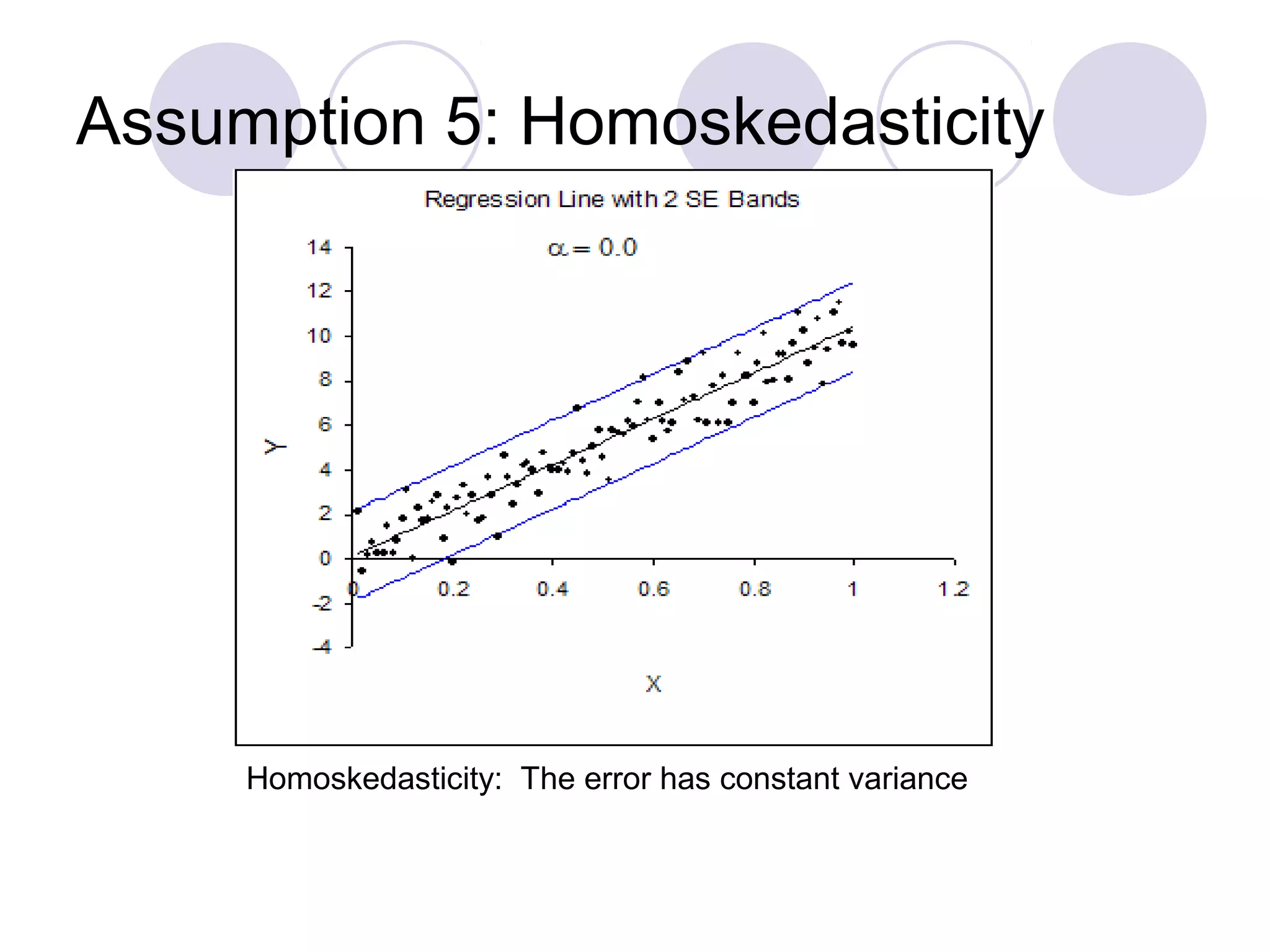
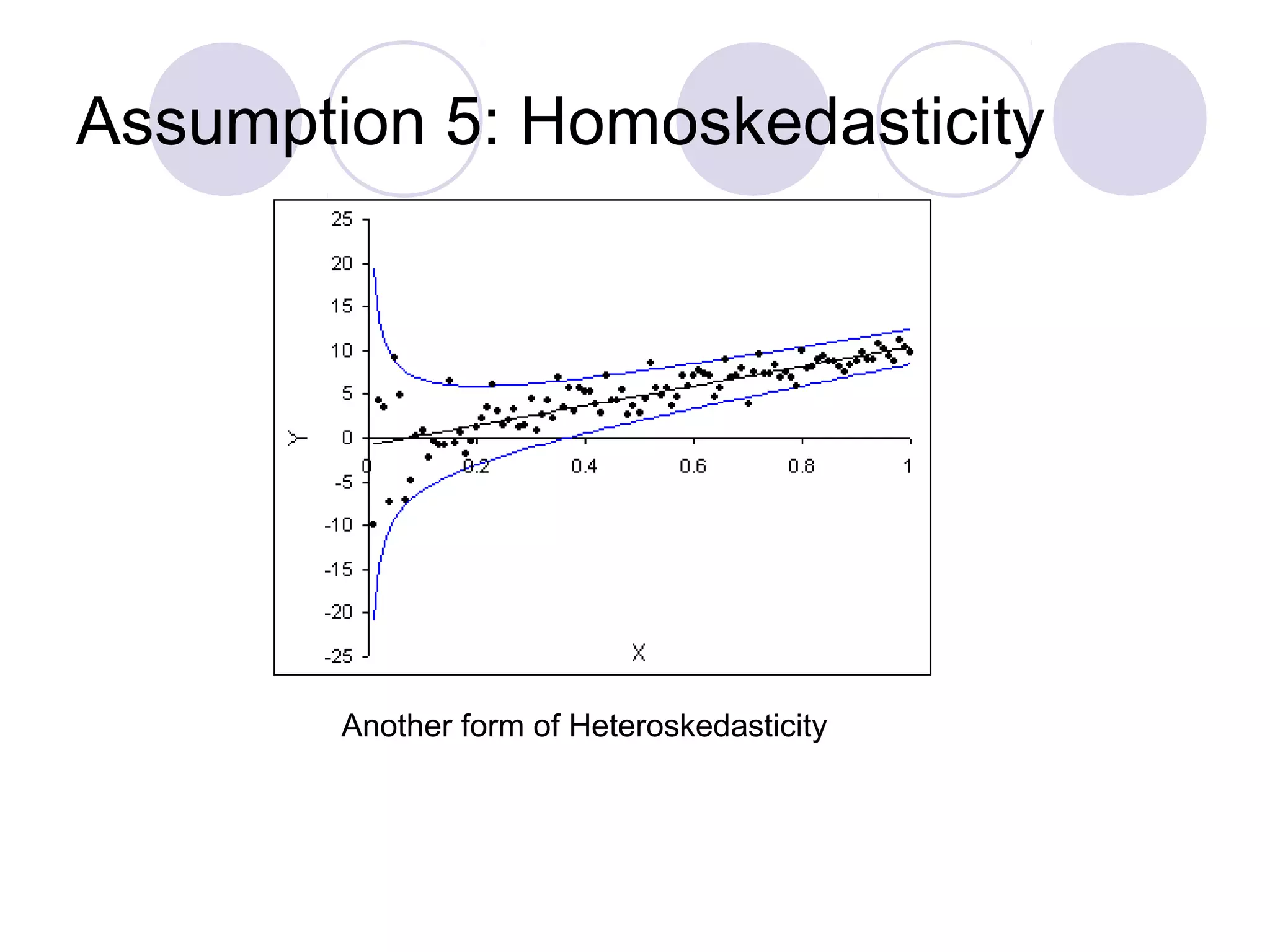
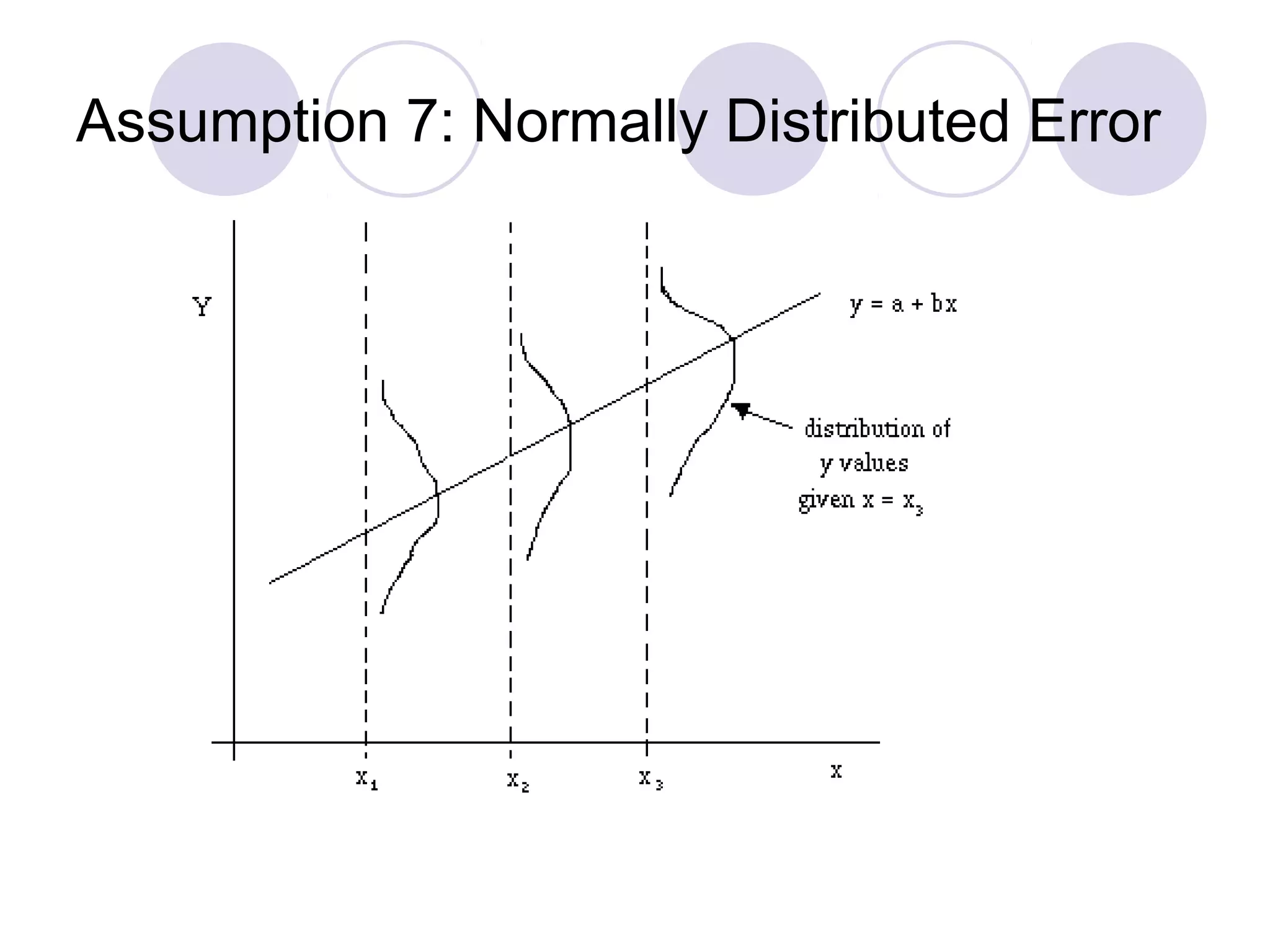
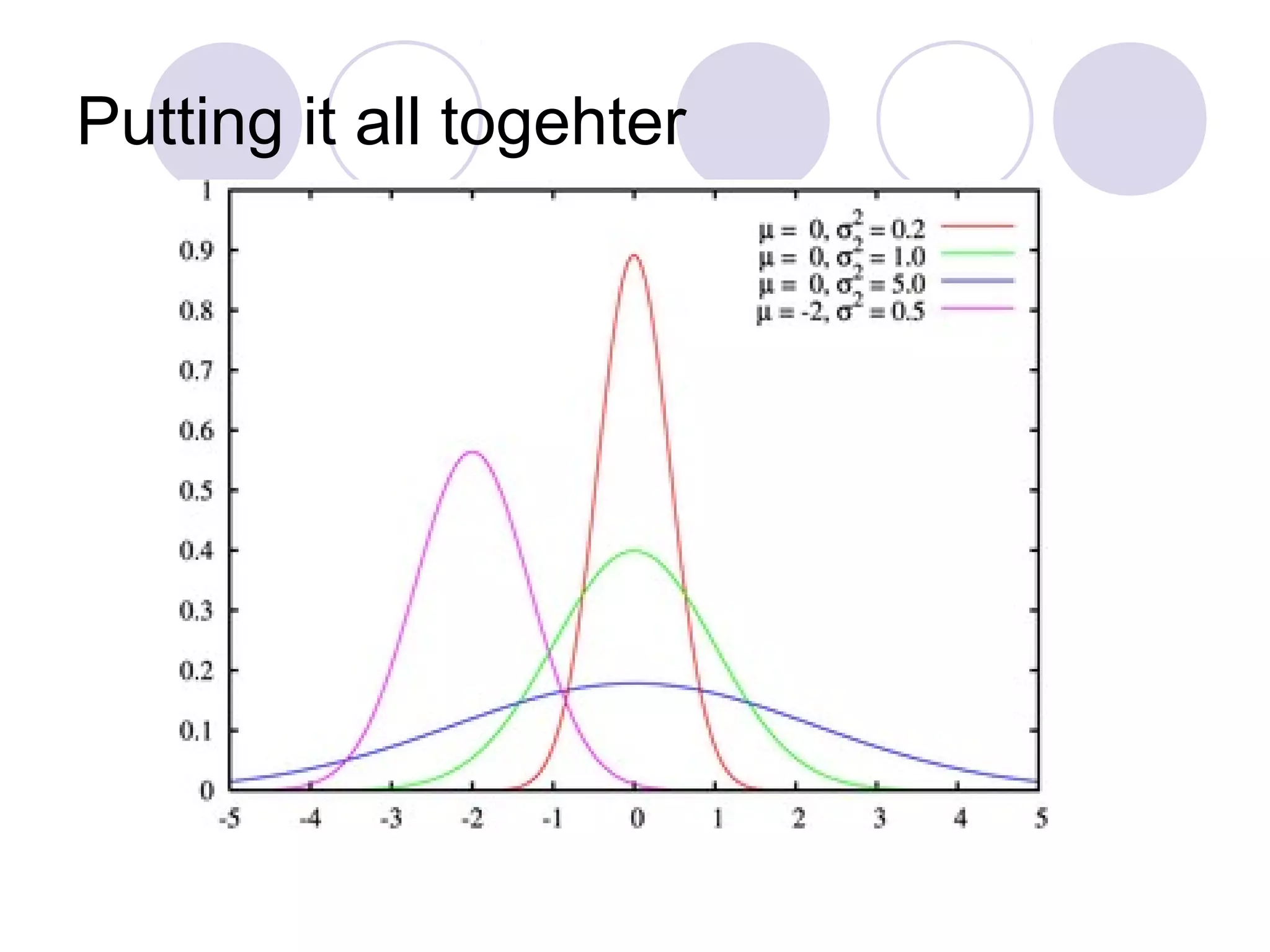
This document summarizes the key assumptions and properties of Ordinary Least Squares (OLS) regression. OLS aims to minimize the sum of squared residuals by estimating the beta coefficients. It provides the best linear unbiased estimates if its assumptions are met. The key assumptions are: 1) the regression is linear in parameters; 2) the error term has a mean of zero; 3) the error term is uncorrelated with the independent variables; 4) there is no serial correlation or autocorrelation in the error term; 5) the error term has constant variance (homoskedasticity); and 6) there is no perfect multicollinearity among independent variables. When all assumptions are met, OLS estimates

1. Lecture 4
Econ 488

2. Ordinary Least Squares (OLS)
Yi = β 0 + β1 X 1i + β 2 X 2i + ... + β K X Ki + ε i
 Objective
of OLS  Minimize the sum of
squared residuals:
min n 2

ˆ ∑ ei
β i =1
where
 Remember
ˆ
ei = Yi − Yi
that OLS is not the only possible
estimator of the βs.
 But OLS is the best estimator under certain
assumptions…

3. Classical Assumptions
 1.
Regression is linear in parameters
 2. Error term has zero population mean
 3. Error term is not correlated with X’s
 4. No serial correlation
 5. No heteroskedasticity
 6. No perfect multicollinearity
 and we usually add:
 7. Error term is normally distributed

4. Assumption 1: Linearity
 The

regression model:
A) is linear

It can be written as
Yi = β 0 + β1 X 1i + β 2 X 2i + ... + β K X Ki + ε i
This doesn’t mean that the theory must be linear
 For example… suppose we believe that CEO salary is
related to the firm’s sales and CEO’s tenure.
 We might believe the model is:
log( salary ) i = β 0 + β1 log( salesi ) + β 2tenurei + β 3tenure 2 i + ε i


5. Assumption 1: Linearity
 The

regression model:
B) is correctly specified
The model must have the right variables
 No omitted variables
 The model must have the correct functional form
 This is all untestable  We need to rely on economic
theory.


6. Assumption 1: Linearity
 The

regression model:
C) must have an additive error term

The model must have + εi

7. Assumption 2: E(εi)=0
 Error
term has a zero population mean
 E(εi)=0
 Each
observation has a random error with
a mean of zero
 What if E(εi)≠0?
 This
is actually fixed by adding a constant
(AKA intercept) term

8. Assumption 2: E(εi)=0
 Example:
Suppose instead the mean of εi
was -4.
 Then we know E(εi+4)=0
 We
can add 4 to the error term and
subtract 4 from the constant term:
 Yi =β0+ β1Xi+εi
 Yi
=(β0-4)+ β1Xi+(εi+4)

9. Assumption 2: E(εi)=0
 Yi
=β0+ β1Xi+εi
 Yi
=(β0-4)+ β1Xi+(εi+4)
 We
can rewrite:
 Yi =β0*+ β1Xi+εi*
 Where
 Now
β0*= β0-4
and
εi*=εi+4
E(εi*)=0, so we are OK.

10. Assumption 3: Exogeneity
 Important!!
 All
explanatory variables are uncorrelated
with the error term
 E(εi|X1i,X2i,…, XKi,)=0
 Explanatory
variables are determined
outside of the model (They are
exogenous)

11. Assumption 3: Exogeneity
 What
happens if assumption 3 is violated?
 Suppose we have the model,
 Yi =β0+ β1Xi+εi
 Suppose
 When
well.
Xi and εi are positively correlated
Xi is large, εi tends to be large as

12. Assumption 3: Exogeneity
120
100
“True” Line
80
60
“True Line”
40
20
0
0
-20
-40
5
10
15
20
25

13. Assumption 3: Exogeneity
120
100
Data
Data
80
“True” Line
60
“True Line”
“True Line”
40
20
0
0
-20
-40
5
10
15
20
25

14. Assumption 3: Exogeneity
120
Estimated Line
100
Data
80
60
“True Line”
40
20
0
0
-20
-40
5
10
15
20
25

15. Assumption 3: Exogeneity
 Why
would x and ε be correlated?
 Suppose you are trying to study the
relationship between the price of a
hamburger and the quantity sold across a
wide variety of Ventura County
restaurants.

16. Assumption 3: Exogeneity
 We
estimate the relationship using the
following model:
 salesi= β0+β1pricei+εi
 What’s
the problem?

17. Assumption 3: Exogeneity
 What’s
 What
the problem?
else determines sales of hamburgers?
 How would you decide between buying a burger
at McDonald’s ($0.89) or a burger at TGI
Fridays ($9.99)?
 Quality differs
 sales = β +β price +ε  quality isn’t an X variable
i
0
1
i
i
even though it should be.
 It becomes part of ε
i

18. Assumption 3: Exogeneity
 What’s
 But
the problem?
price and quality are highly positively
correlated
 Therefore x and ε are also positively correlated.
 This means that the estimate of β will be too
1
high
 This is called “Omitted Variables Bias” (More in
Chapter 6)

19. Assumption 4: No Serial Correlation
 Serial
Correlation: The error terms across
observations are correlated with each
other
 i.e. ε1 is correlated with ε2, etc.
 This
is most important in time series
 If errors are serially correlated, an
increase in the error term in one time
period affects the error term in the next.

20. Assumption 4: No Serial Correlation
The assumption that there is no serial
correlation can be unrealistic in time series
 Think of data from a stock market…


21. Real S&P 500 Stock Price Index
Assumption 4: No Serial Correlation
2000
1500
1000
Price
500
0
1870
-500
1920
1970
Year
Stock data is serially correlated!
2020

22. Assumption 5: Homoskedasticity
 Homoskedasticity:
The error has a
constant variance
 This is what we want…as opposed to
 Heteroskedasticity: The variance of the
error depends on the values of Xs.

23. Assumption 5: Homoskedasticity
Homoskedasticity: The error has constant variance

24. Assumption 5: Homoskedasticity
Heteroskedasticity: Spread of error depends on X.

25. Assumption 5: Homoskedasticity
Another form of Heteroskedasticity

26. Assumption 6: No Perfect Multicollinearity
 Two
variables are perfectly collinear if one
can be determined perfectly from the other
(i.e. if you know the value of x, you can
always find the value of z).
 Example: If we regress income on age,
and include both age in months and age in
years.
 But
age in years = age in months/12
 e.g. if we know someone is 246 months old, we
also know that they are 20.5 years old.

27. Assumption 6: No Perfect Multicollinearity
 What’s
wrong with this?
 incomei= β0 + β1agemonthsi +
β2ageyearsi + εi
 What is β1?
 It is the change in income associated with
a one unit increase in “age in months,”
holding age in years constant.
 But
if you hold age in years constant, age in
months doesn’t change!

28. Assumption 6: No Perfect Multicollinearity
 β1 =
Δincome/Δagemonths
 Holding
Δageyears = 0
 If Δageyears = 0; then Δagemonths = 0
 So β1 = Δincome/0
 It
is undefined!

29. Assumption 6: No Perfect Multicollinearity
 When
more than one independent variable
is a perfect linear combination of the other
independent variables, it is called Perfect
MultiCollinearity
 Example: Total Cholesterol, HDL and LDL
 Total Cholesterol = LDL + HDL
 Can’t include all three as independent
variables in a regression.
 Solution: Drop one of the variables.

30. Assumption 7: Normally Distributed Error

31. Assumption 7: Normally Distributed Error
 This
is required not required for OLS, but it
is important for hypothesis testing
 More on this assumption next time.

32. Putting it all together
 Last
class, we talked about how to compare
estimators. We want:
ˆ
 1. β is unbiased.


ˆ
E (β ) = β
on average, the estimator is equal to the population
value
ˆ
 2. β

is efficient
The variance of the estimator is as small as possible

33. Putting it all togehter

34. Gauss-Markov Theorem
 Given
OLS assumptions 1 through 6, the
OLS estimator of βk is the minimum
variance estimator from the set of all linear
unbiased estimators of βk for k=0,1,2,…,K
 OLS
is BLUE
 The Best, Linear, Unbiased Estimator

35. Gauss-Markov Theorem
 What
happens if we add assumption 7?
 Given assumptions 1 through 7, OLS is
the best unbiased estimator
 Even out of the non-linear estimators
 OLS is BUE?

36. Gauss-Markov Theorem
 With
Assumptions 1-7 OLS is:
ˆ
 1. Unbiased: E ( β ) = β
 2. Minimum Variance – the sampling distribution
is as small as possible
 3. Consistent – as n∞, the estimators
converge to the true parameters

 4.
As n increases, variance gets smaller, so each estimate
approaches the true value of β.
Normally Distributed. You can apply
statistical tests to them.