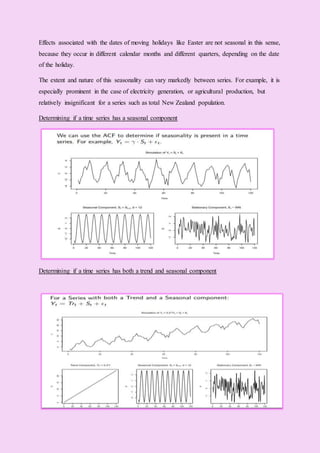
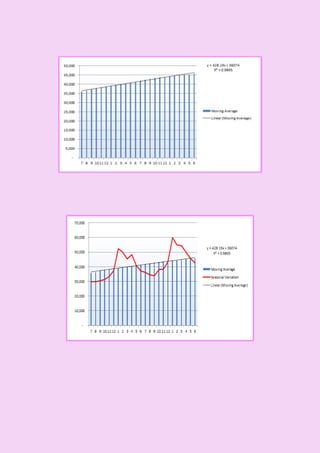
This document discusses trend and seasonal components in time series analysis. It defines trend as the long-term movement in a time series due to underlying economic or socioeconomic factors. Methods for estimating trends include moving averages and least squares. Seasonal components refer to regular fluctuations that occur within the same period each year, such as monthly or quarterly patterns driven by weather, holidays, or other seasonal factors. The document provides examples of trend and seasonal patterns and methods for determining if components are present in a time series, including fitting trend lines using least squares.

1. STATISTICS
TREND AND SEASONAL COMPONENTS
NAME : DWI PUSPITA RINI
NIM : 2201824596
CLASS : LC53
UNIVERSITAS BINA NUSANTARA
JAKARTA
2018

2. TREND COMPONENT (SECULAR TREND or GENERAL
TREND)
What is the trend?
Trend estimates reveal the smooth, relatively slowly changing features in a time series. They
are usually estimated by applying repeated moving averages.
How to use the trend
The trend cycle component shows the fundamental movement of the series, reflecting the
prevailing economic conditions in an economic series. It merges any cyclical movements
present with the underlying trend:
Underlying trend
Most economic time series have a long-term underlying trend present. It is often associated
with some basic characteristic of the economy, such as population growth. In some series the
trend may be steadily upwards, while in others it may show considerable variability. In
general the trend has little effect on the short-term month-to-month movements of the series,
but it is the most important component for determining the general level and broader
movement of the activity as measured by the series.
The secular trend is the main component of a time series which results from long term effect
of socio-economic and political factors. This trend may show the growth or decline in a time
series over a long period. This is the type of tendency which continues to persist for a very
long period. Prices, export and imports data, for example, reflect obviously increasing
tendencies over time.
The trend is the long term pattern of a time series. A trend can be positive or negative
depending on whether the time series exhibits an increasing long term pattern or a decreasing
long term pattern. If a time series does not show an increasing or decreasing pattern then the
series is stationary in the mean.

3. Trend Component
A long-term increase or decrease in the data which might not be linear. Sometimes the trend
might change direction as time increases.
Trend
Long term behavior e.g. several years
TREND
The trend is the long-term movement of a time series. Any increase or decrease in the values
of a variable occurring over a period of several years gives a trend. If the values of a
variables remain statutory over several years, then no trend can be observed in the time
series. To study the growth in industrial production from the year 1995 to 2005, we need to
find the trend values in industrial production for this time period which may be increasing or
decreasing. These trends may be either linear or non-linear. There are other types of trends
like parabolic (or quadratic) and logarithmic (or exponential). However we are more
concerned here with straight line (i.e. linear) trends.
The various methods of fitting a straight line to a time series such as free hand method, the
method of semi-averages, the method of moving averages and the method of least squares.
a. The Freehand Method
It is the simplest method of finding a trend line. The procedure involves first the
plotting of the time series on a graph and fitting a straight line through the plotted
points in such a way that the straight line shows the trends of the series.
b. The Method of Semi-averages
When the method of semi-averages is used, the given time series is divided into two
parts preferably with the same number of years. The average of each part is calculated
and then a trend line through these average is filled.
c. The method of moving average
The method of moving averages is used not only to fit trend lines but also to seasonal
and cyclical variation.

4. d. Effective Application of Moving Average Method
To ensure result of moving average method to be appropriate and effective, it is
required to ascertain first whether a regular periodic cycle in the time series exists. In
several cases one would find that there is a certain regularity in the series to allow the
use of the moving average method. If may be also noted that if the basis nature of the
time series is linear, it will give a linear trend. In case of curvilinear nature, the trend
will be curve. Moreover moving average method helps to element seasonal
fluctuation, for a time series.
e. Method of Least squares
Among the method of fitting straight line to a series of data, this method is the most
frequently used method. The equation of a straight line is Y = a+ b´ where X is the
time period, say, year and Y is the value of the item measured against time, a is the Y-
intercept and b is the coefficient of X indicating slope of the trend line.
Determining if a time series has a trend component

5. SEASONAL COMPONENT (SEASONAL MOVEMENTS)
What is the seasonal component?
It is the seasonal patterns found in many sub-annual (quarterly or monthly) economic series.
It is reasonably stable in terms of annual timing, direction, and magnitude.
Seasonality occurs when the time series exhibits regular fluctuations during the same month
(or months) every year, or during the same quarter every year. For instance, retail sales peak
during the month of December.
These are short term movements occurring in a data due to seasonal factors. The short term is
generally considered as a period in which changes occur in a time series with variations in
weather or festivities. For example, it is commonly observed that the consumption of ice-
cream during summer us generally high and hence sales of an ice-cream dealer would be
higher in some months of the year while relatively lower during winter months. Employment,
output, export etc. are subjected to change due to variation in weather. Similarly sales of
garments, umbrella, greeting cards and fire-work are subjected to large variation during
festivals like Valentine’s Day, Eid, Christmas, New Year etc. These types of variation in a
time series are isolated only when the series is provided biannually, quarterly or monthly.
Seasonal component
Exists when a series exhibits regular fluctuations based on the season (e.g. every
month/quarter/year). Seasonality is always of a fixed and known period.
Seasonal
Regular behavior within a 12 month period
How does the seasonal component arise?
Possible causes include:
 Natural factors (eg seasonal weather patterns).
 Administrative measures (eg starting and ending dates of the school year).
 Social/cultural/religious traditions (eg fixed holidays such as Christmas).
 The length of the months (28, 29, 30 or 31 days) or quarters (90, 91 or 92 days).

6. Effects associated with the dates of moving holidays like Easter are not seasonal in this sense,
because they occur in different calendar months and different quarters, depending on the date
of the holiday.
The extent and nature of this seasonality can vary markedly between series. For example, it is
especially prominent in the case of electricity generation, or agricultural production, but
relatively insignificant for a series such as total New Zealand population.
Determining if a time series has a seasonal component
Determining if a time series has both a trend and seasonal component

7. EXAMPLE :
TREND
Year: 1991 1992 1993 1994 1995 1996 1997
Profit: 60 72 75 65 80 85 90
Fit a straight line trend by the method of least squares.
Answer: Y = 75.286 + 4.321x, 4.321, 92.57
SEASONAL

9. SOURCE
http://archive.stats.govt.nz/methods/data-analysis/seasonal-adjustment/the-underlying-
model.aspx#trend
http://www.abs.gov.au/websitedbs/D3310114.nsf/home/Time+Series+Analysis:+The+Basics
Brockwell, P. J., & Davis, R. A. (1991). Time Series: Theory and Methods (2nd ed.). New
York: Springer-Verlag