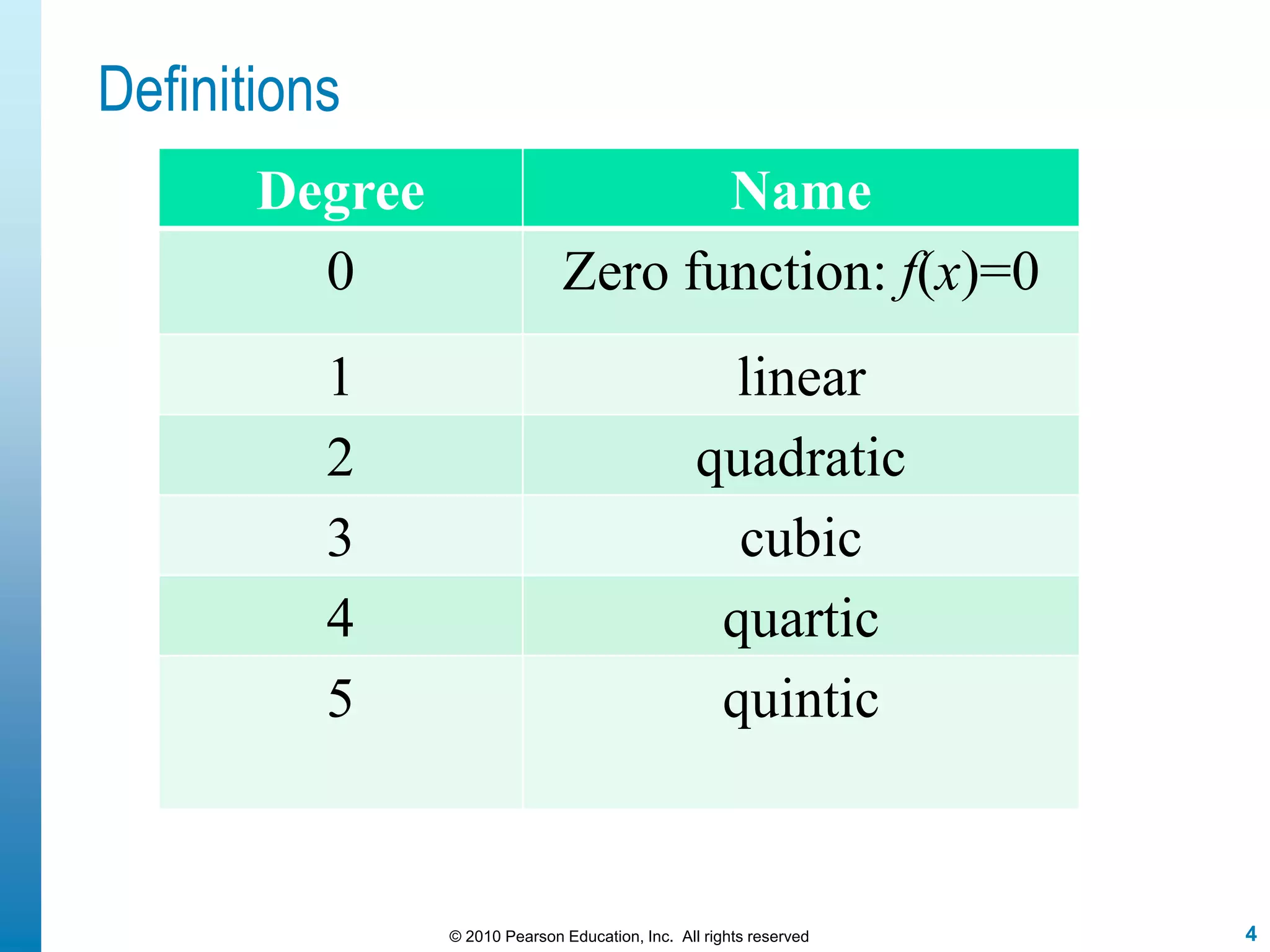
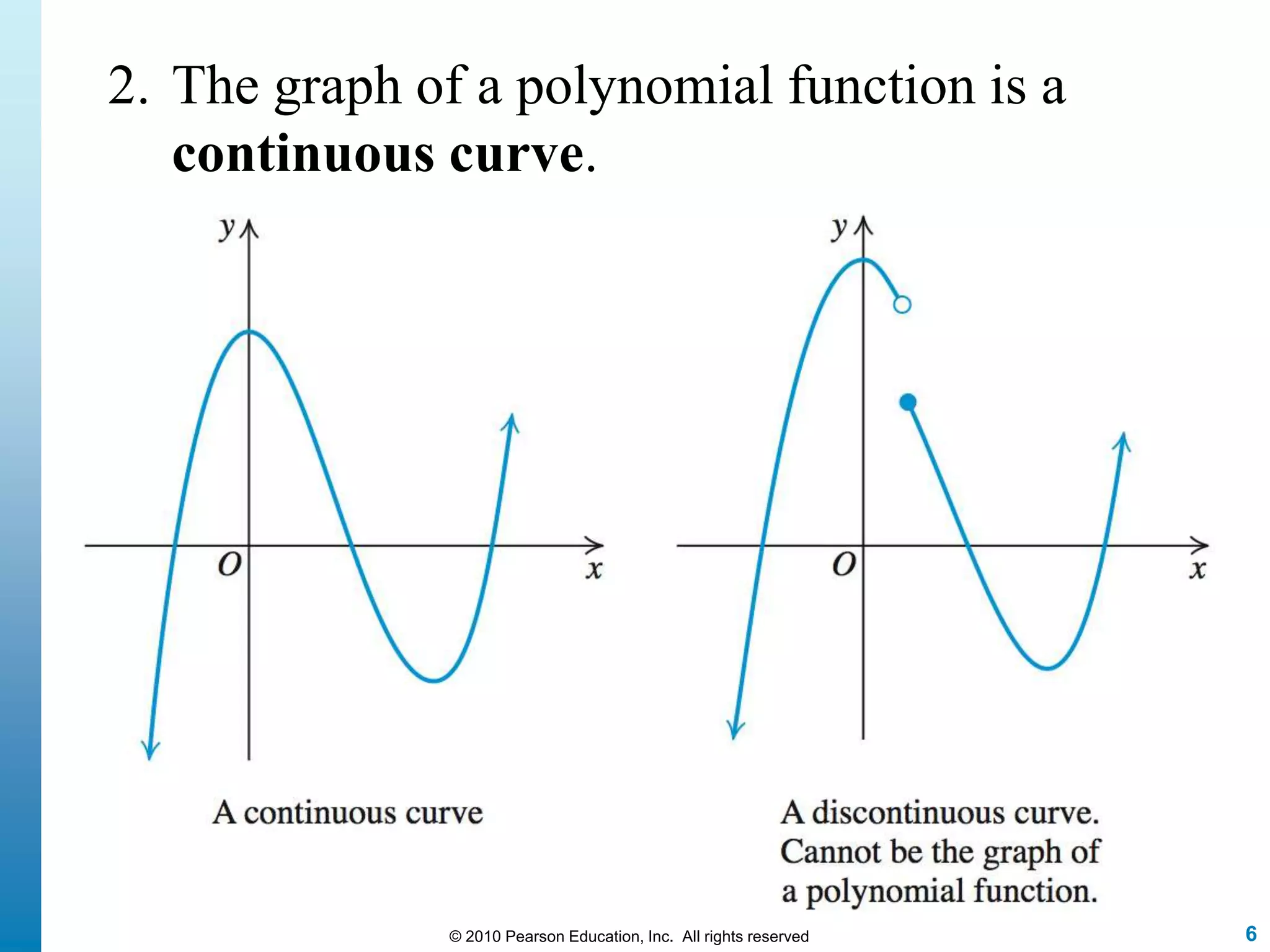
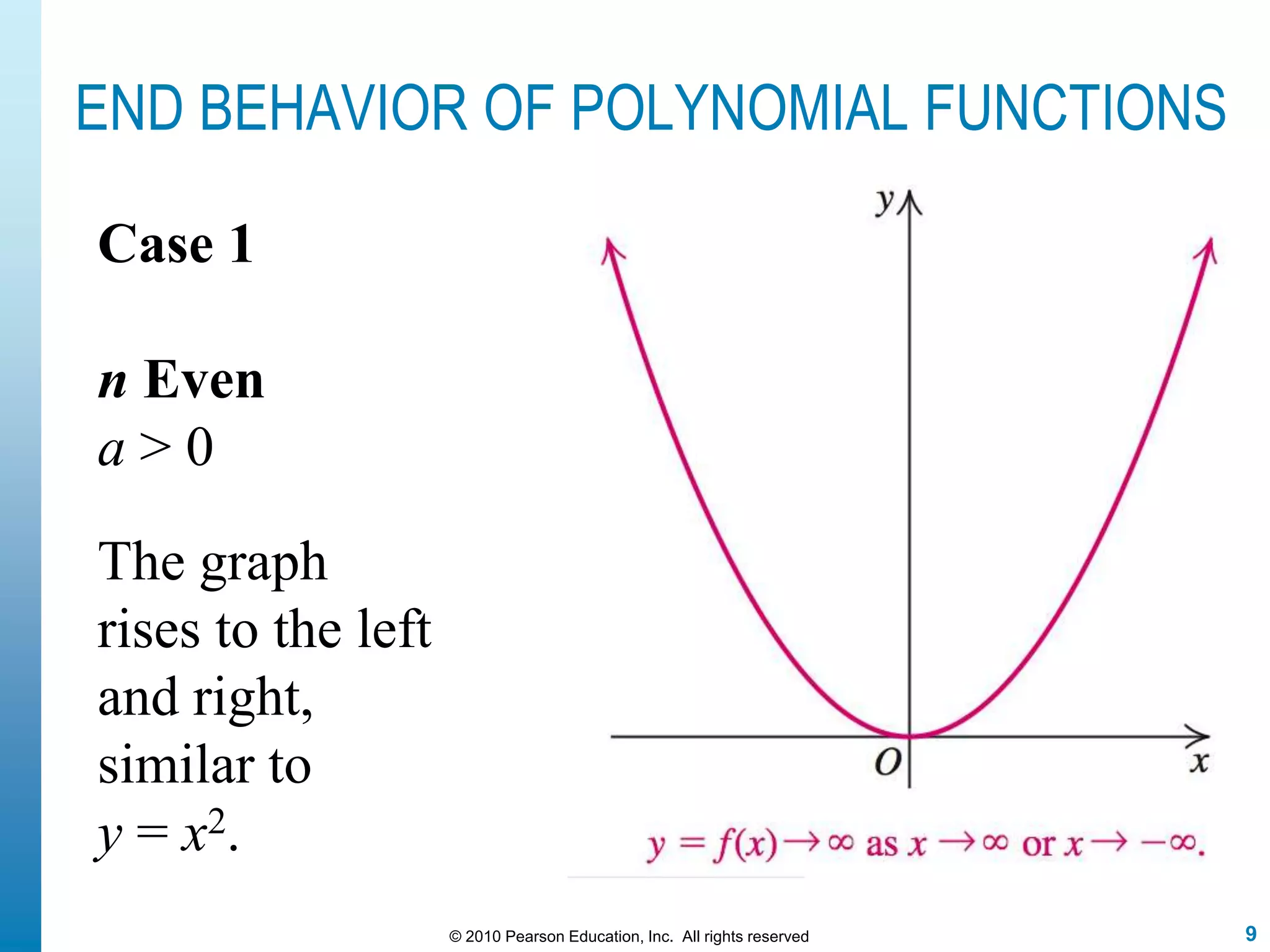
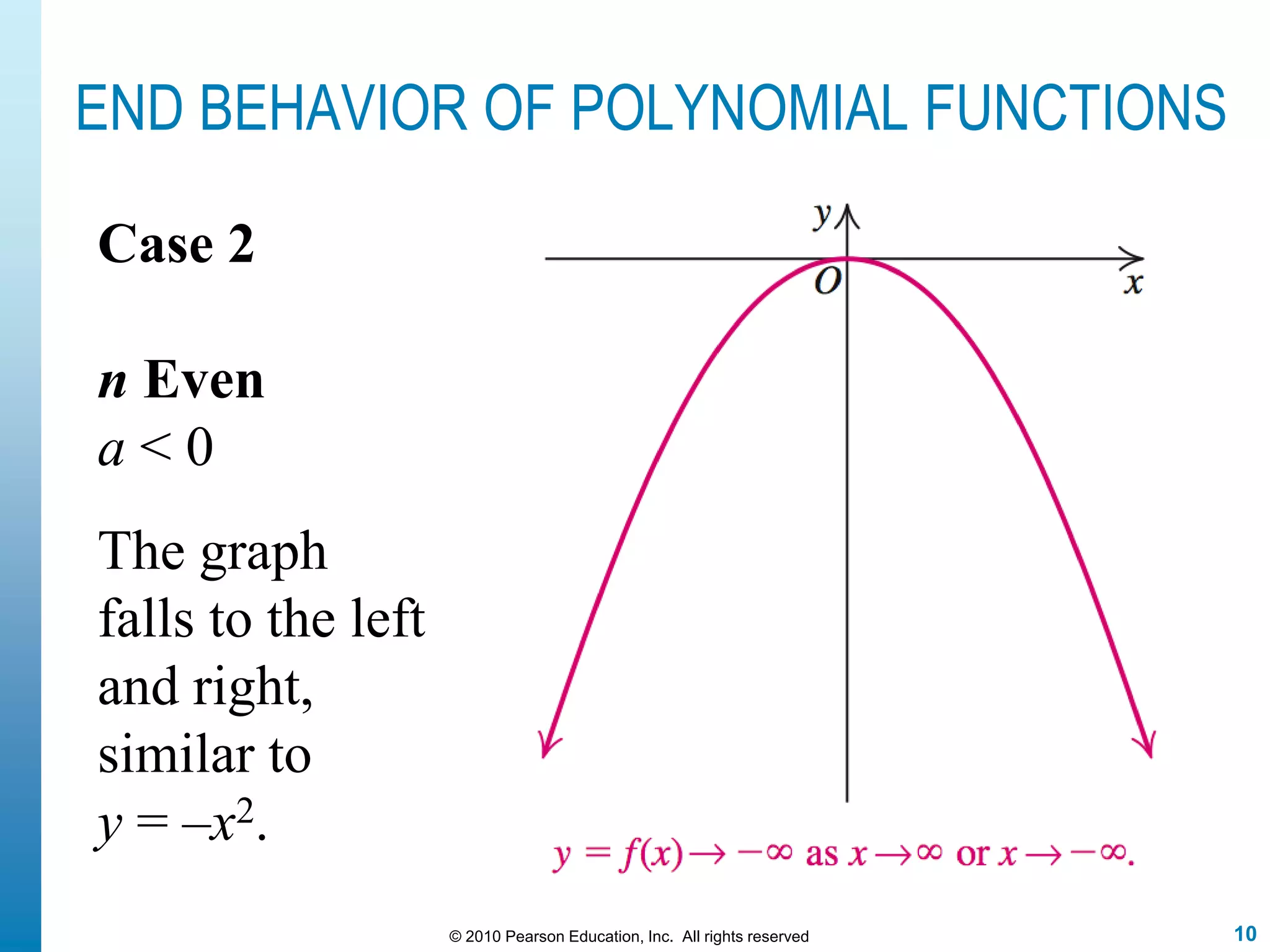
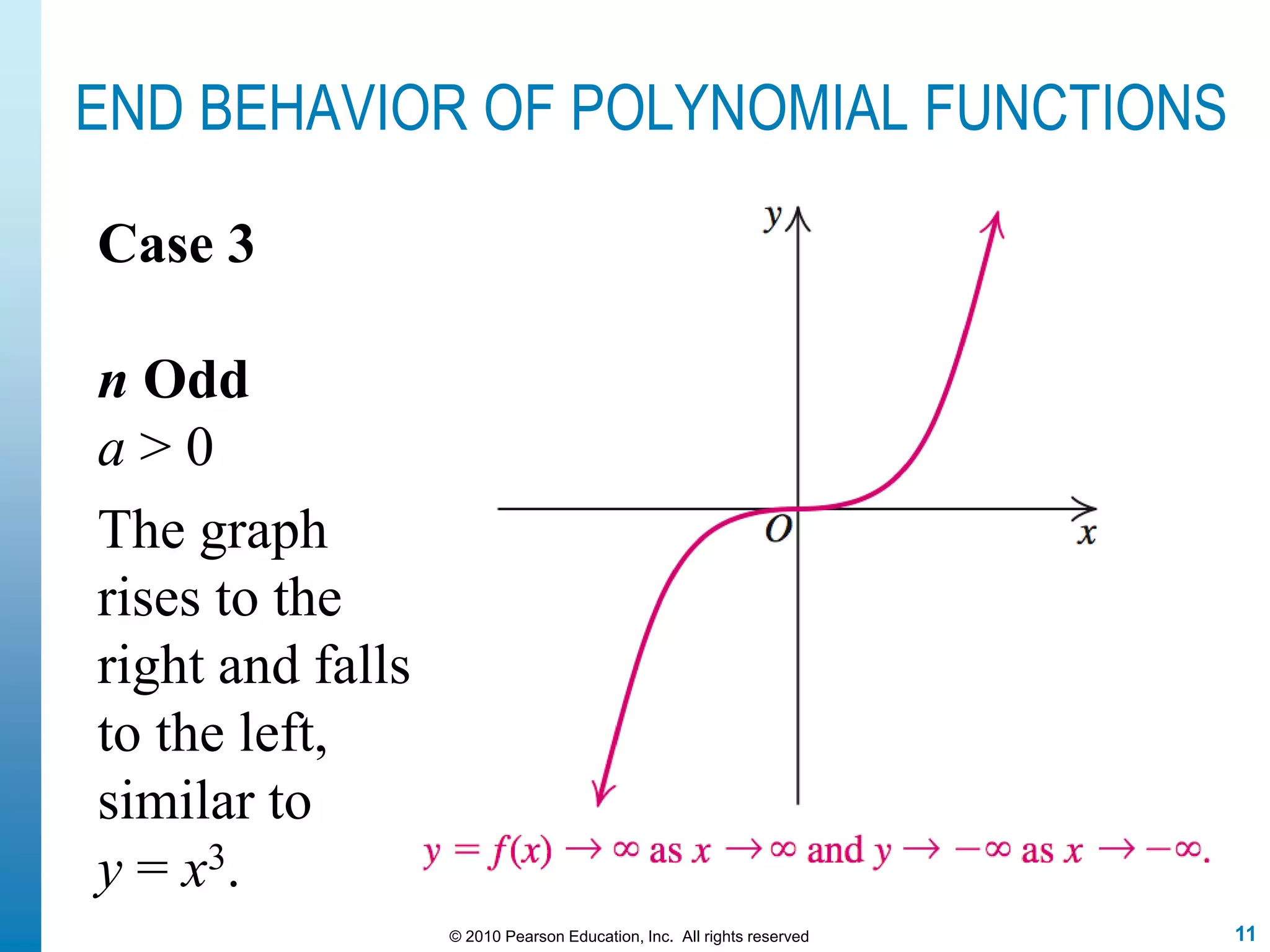
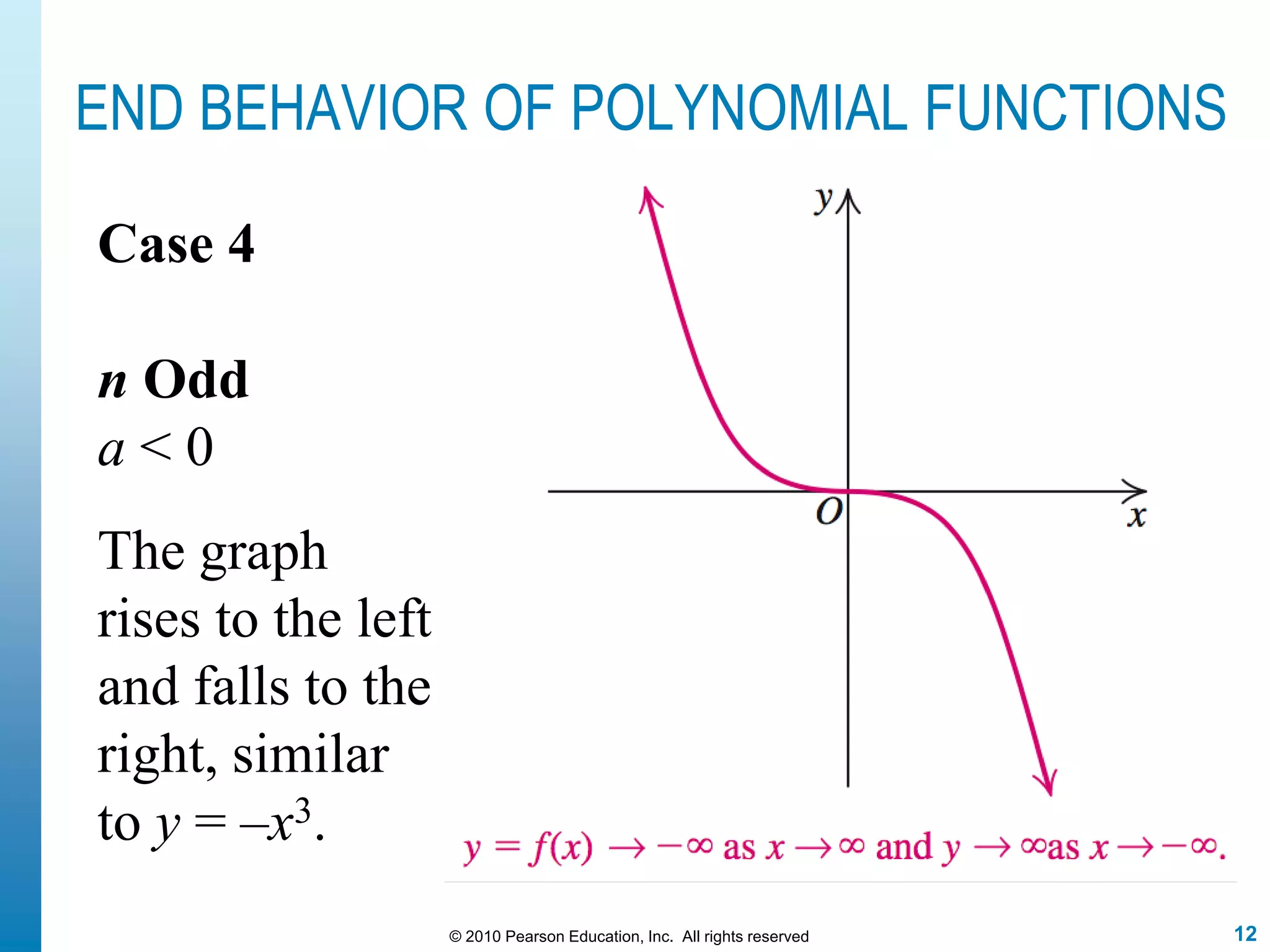
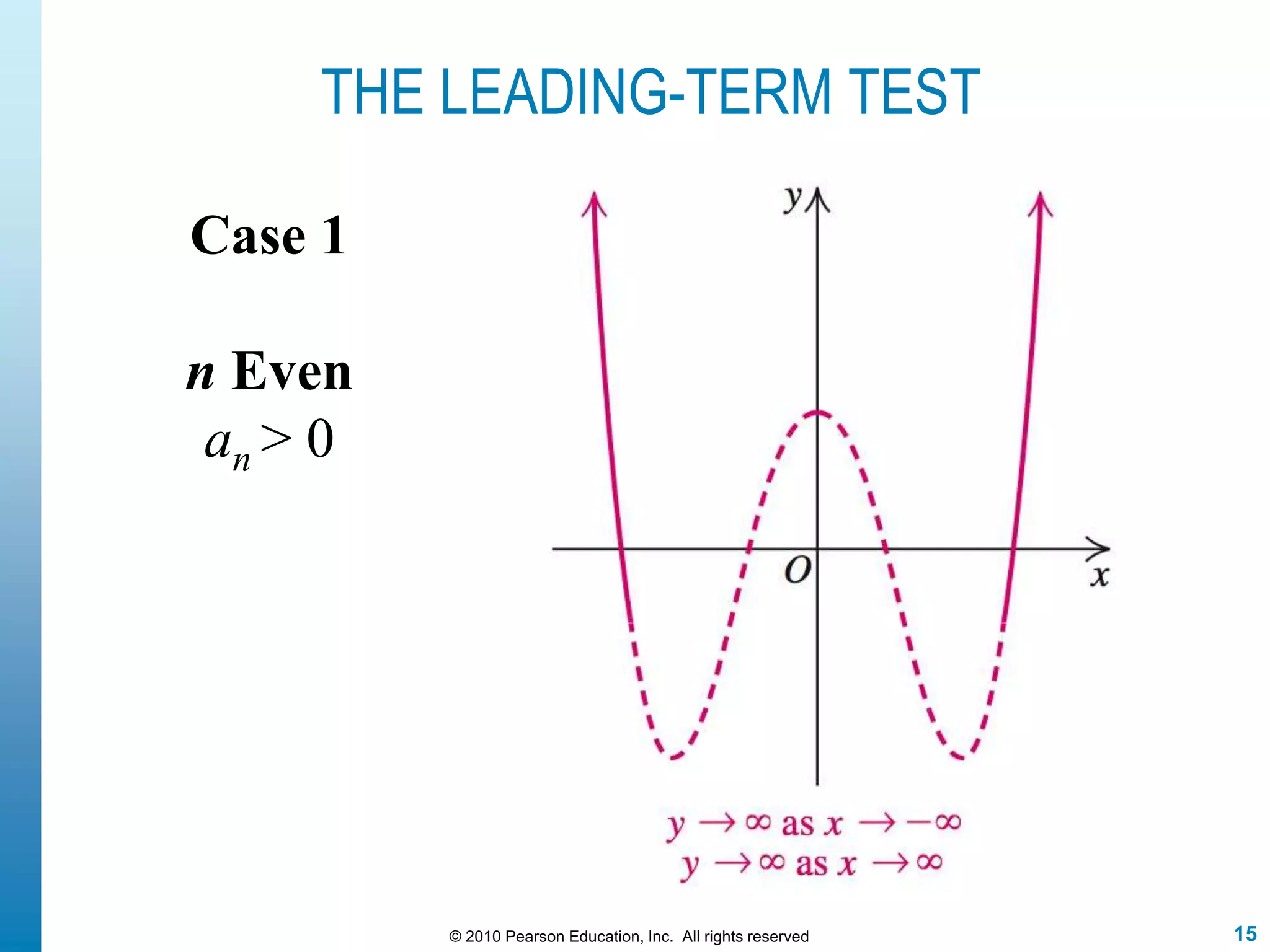
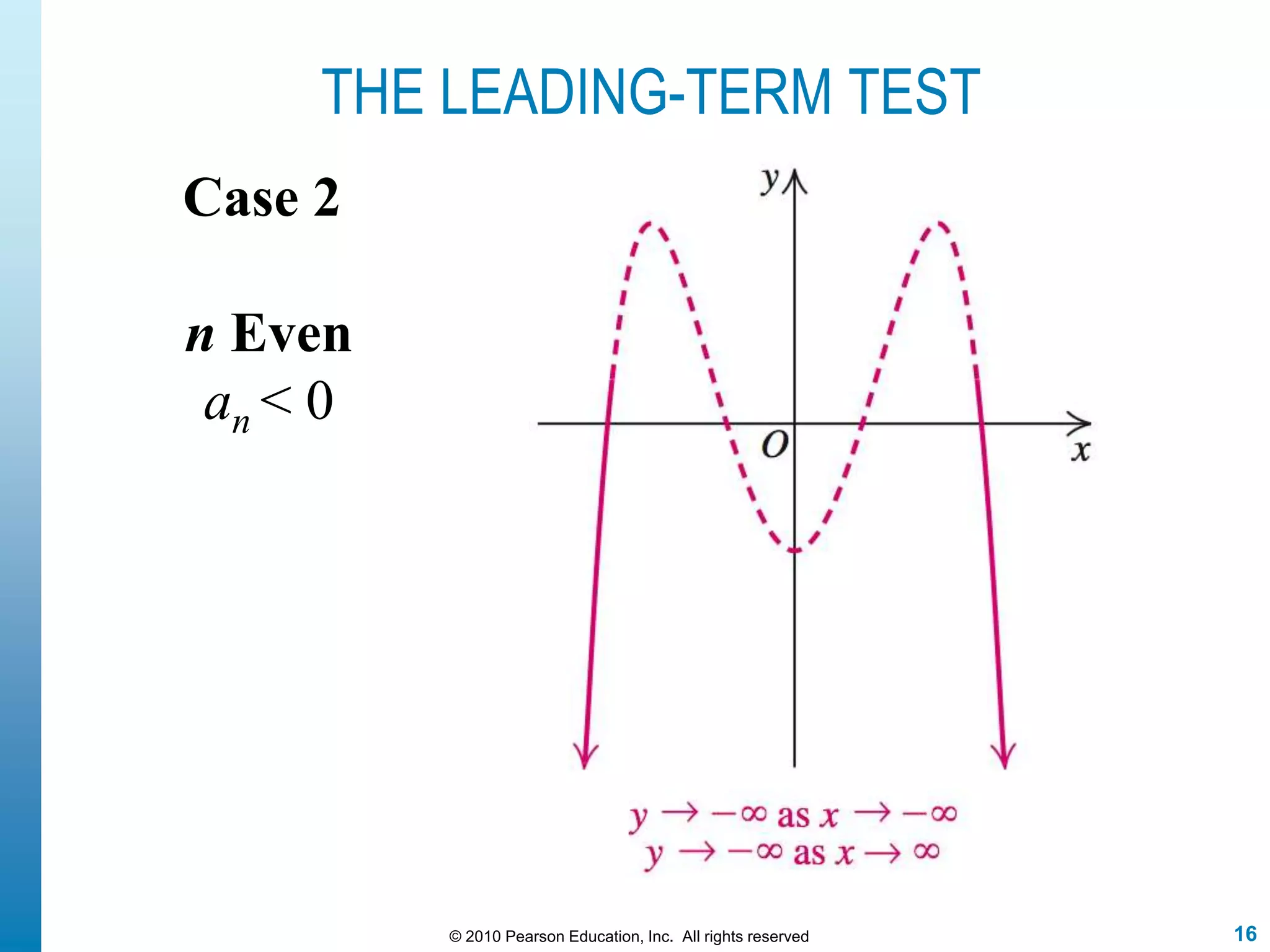
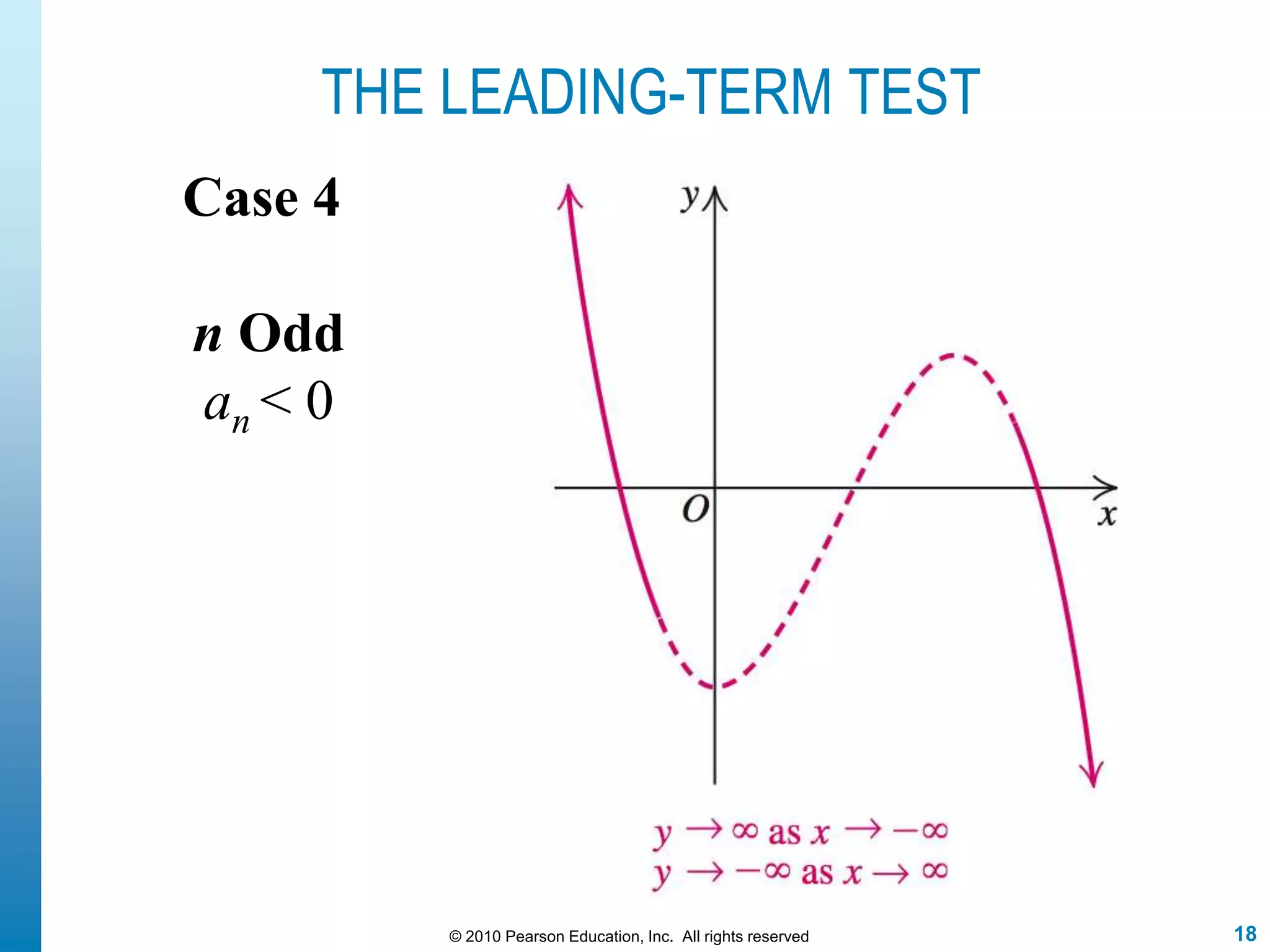
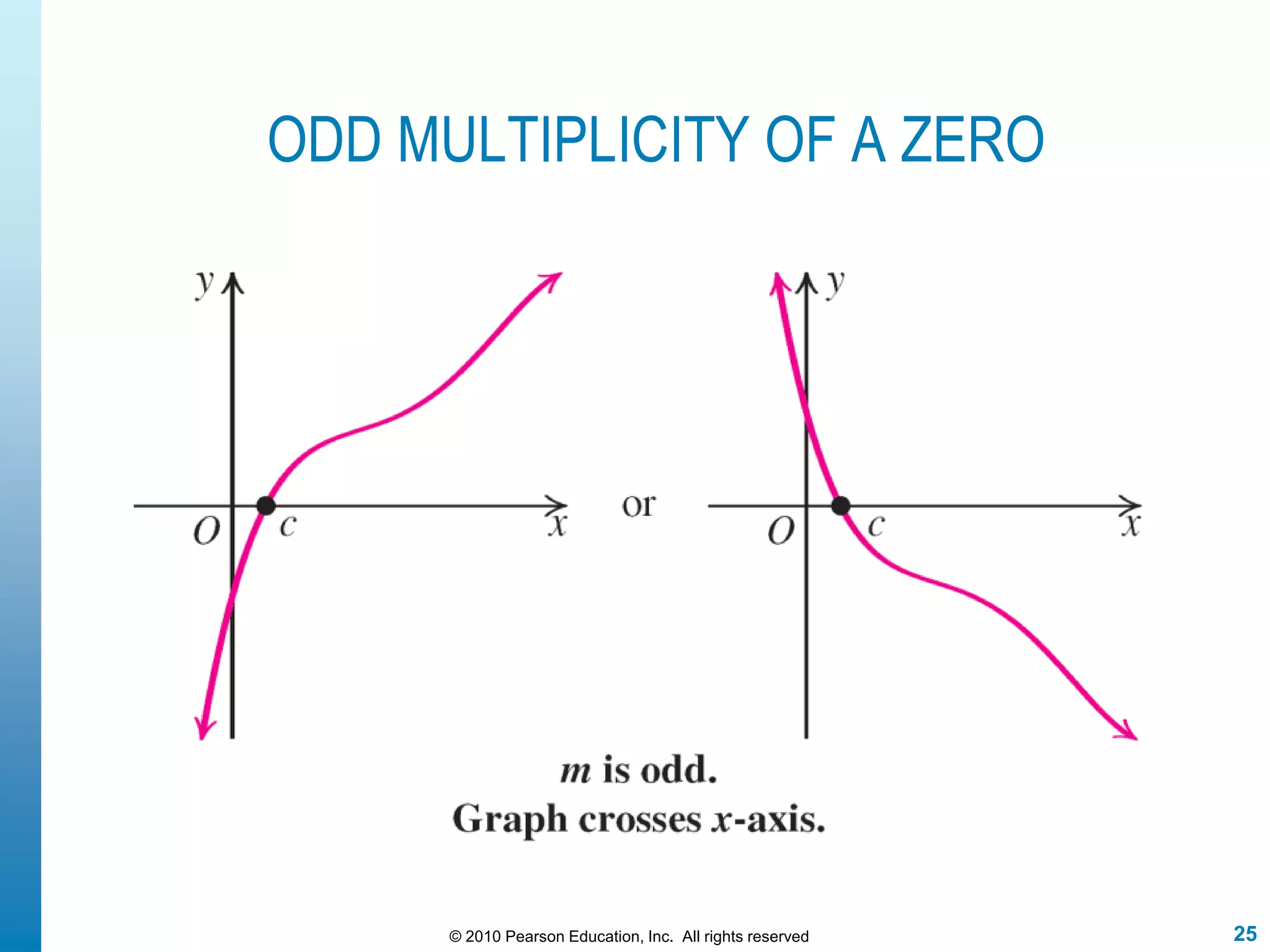
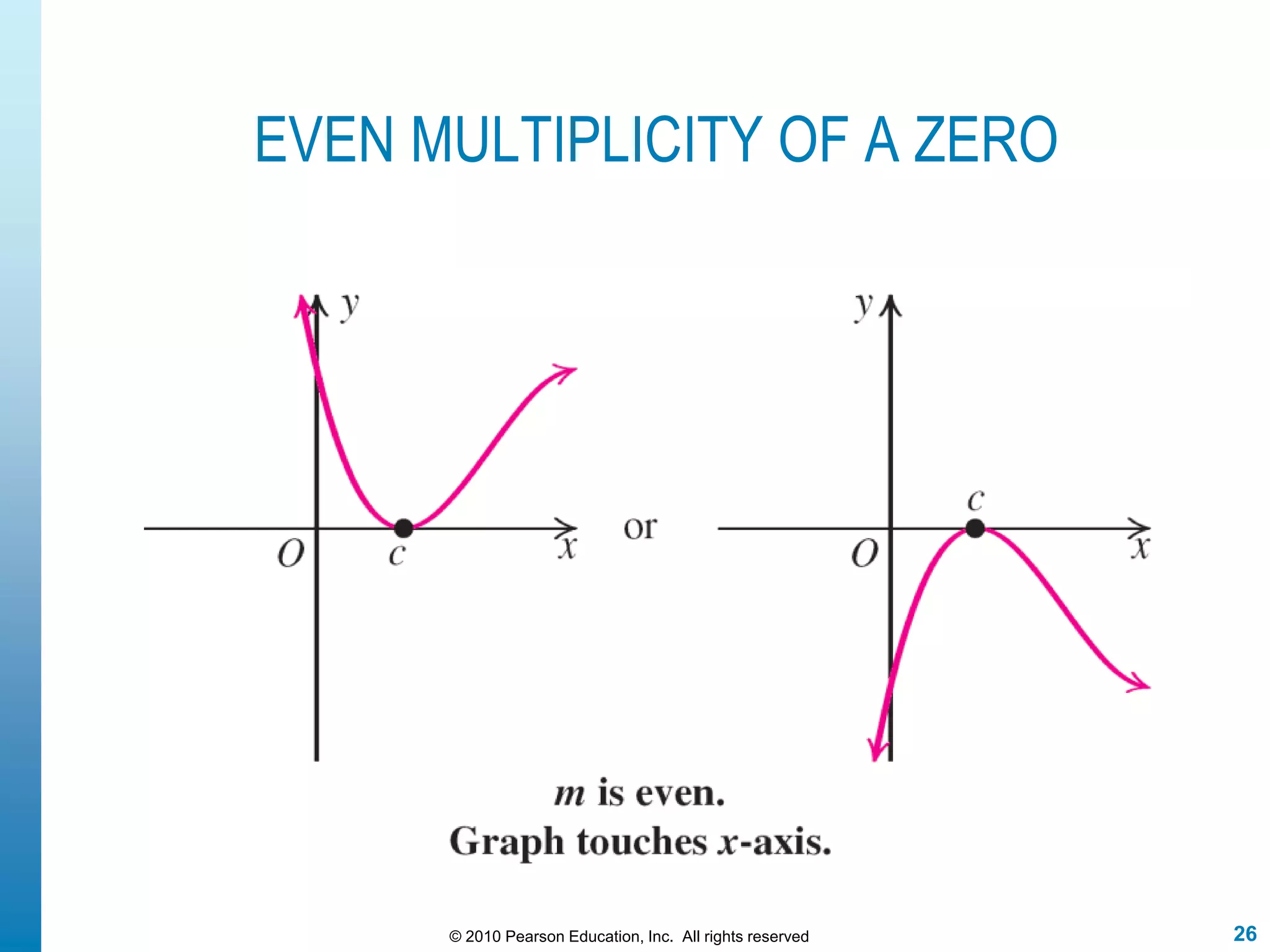
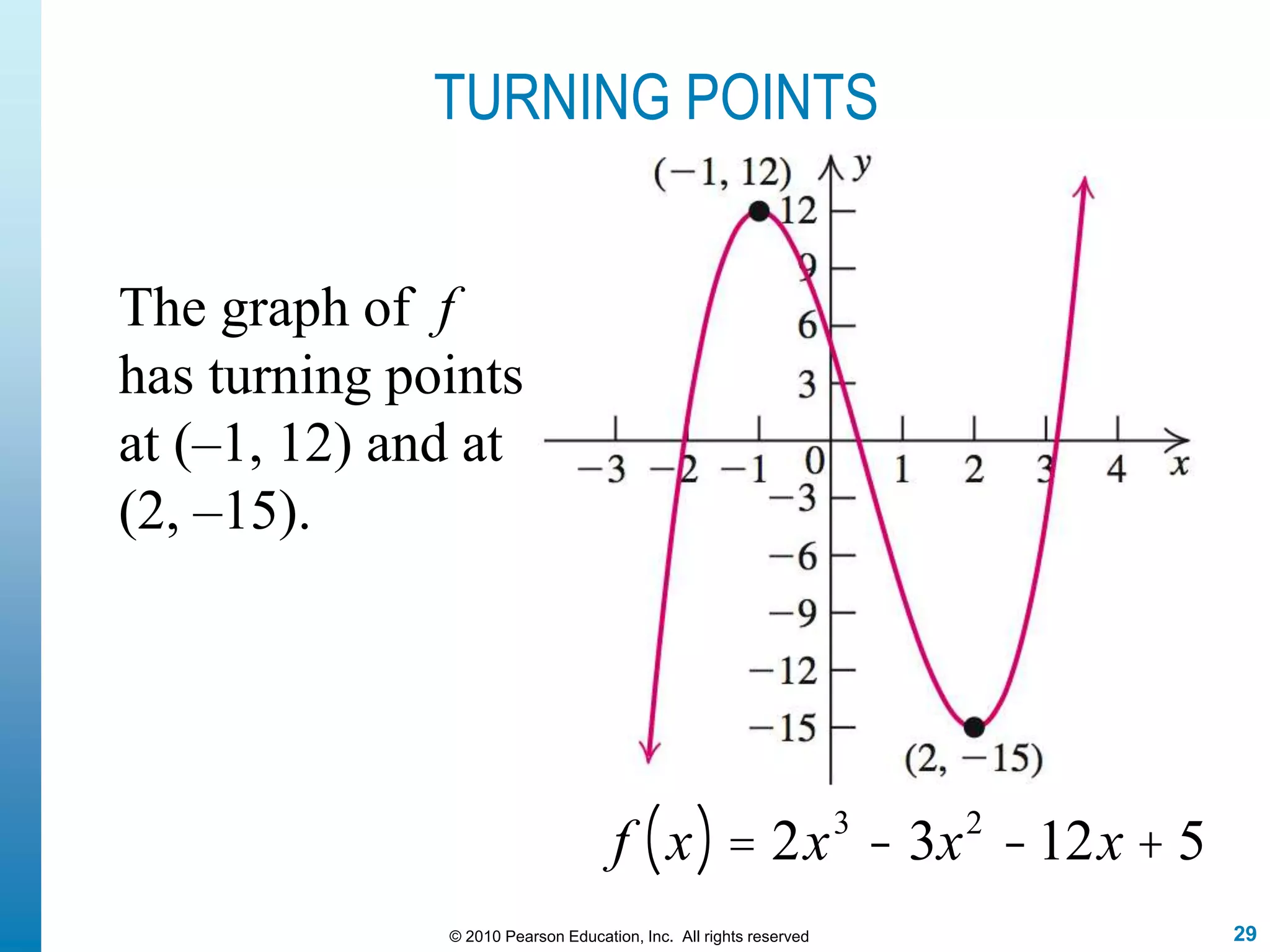
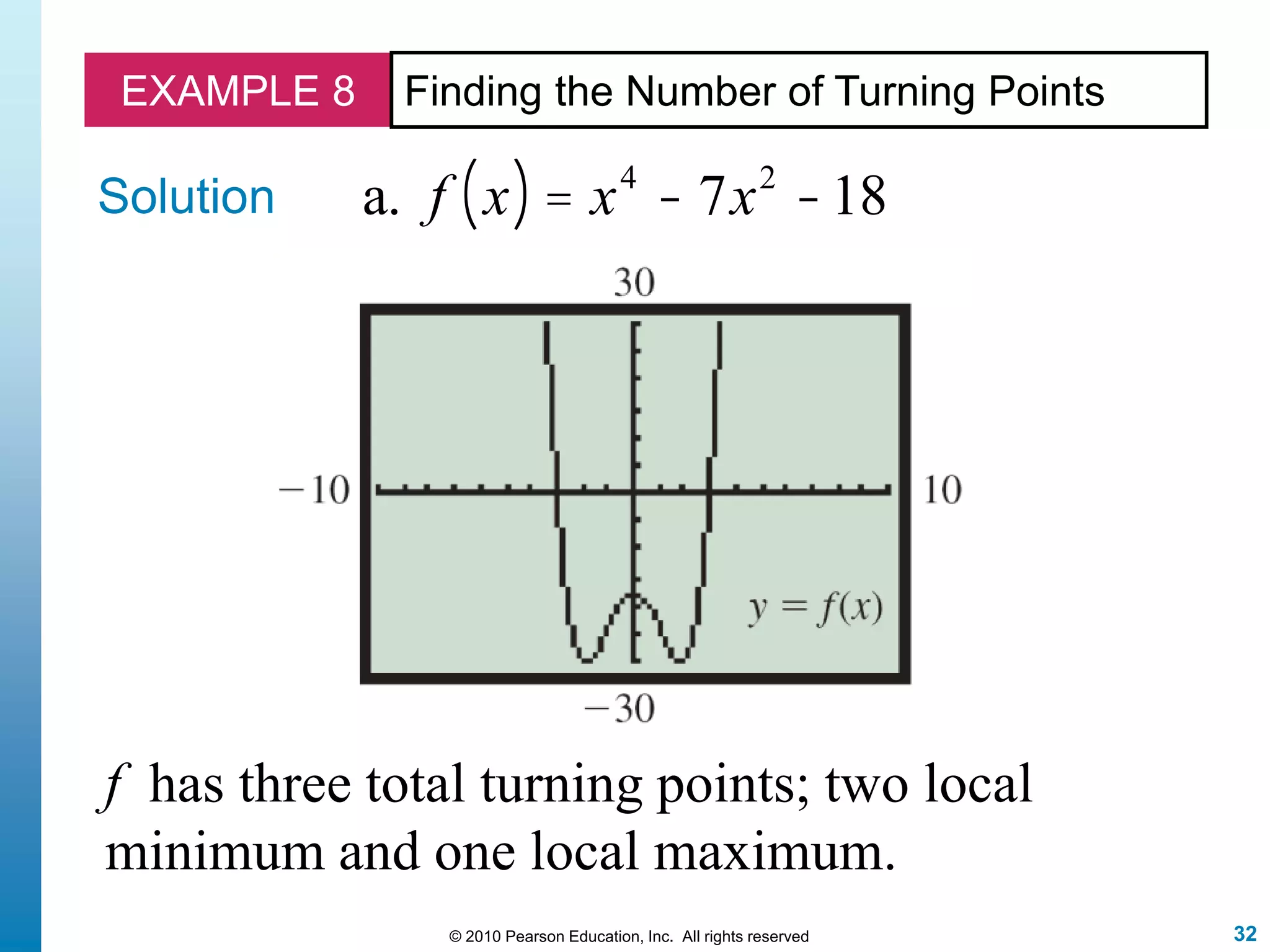
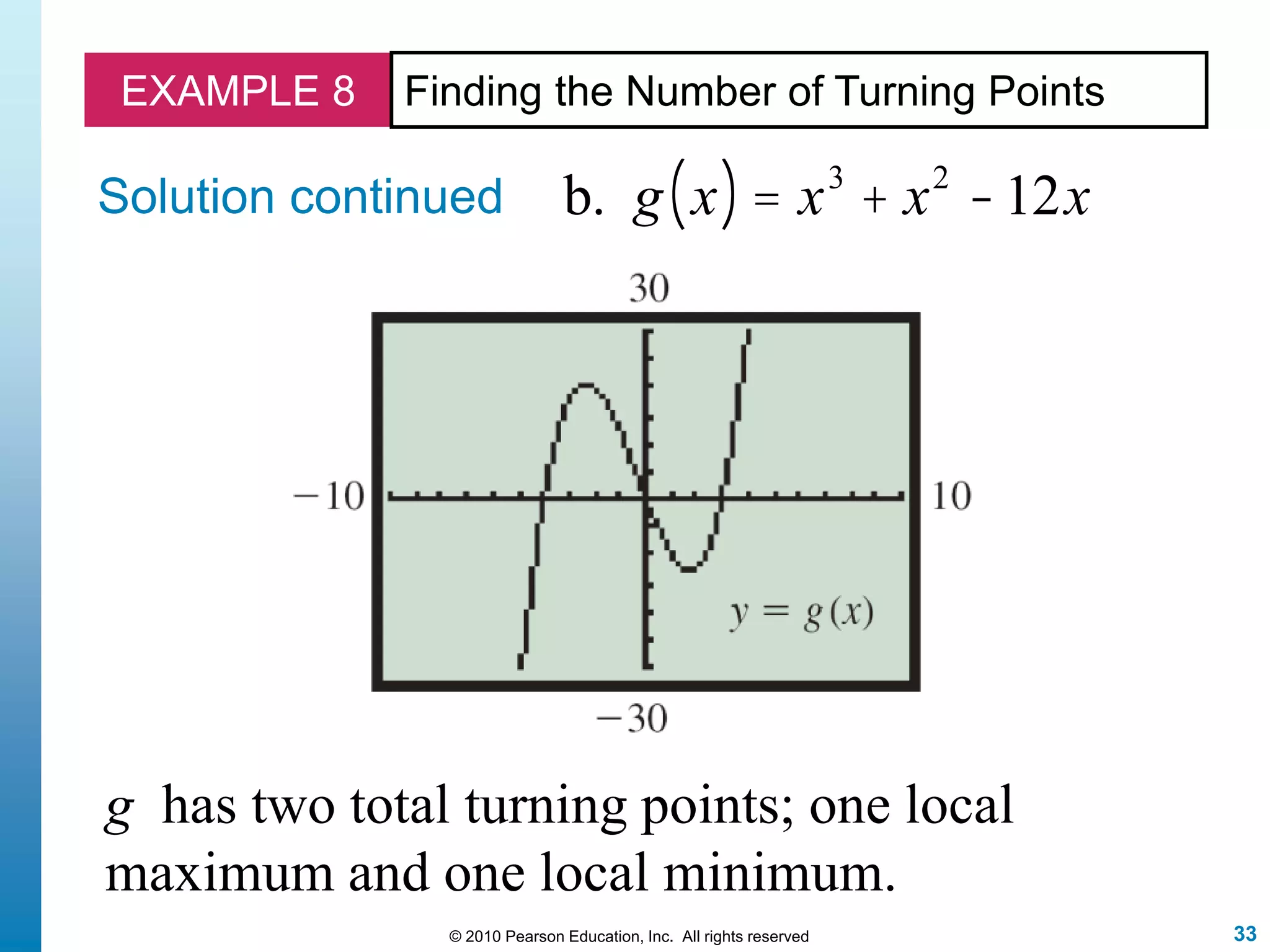
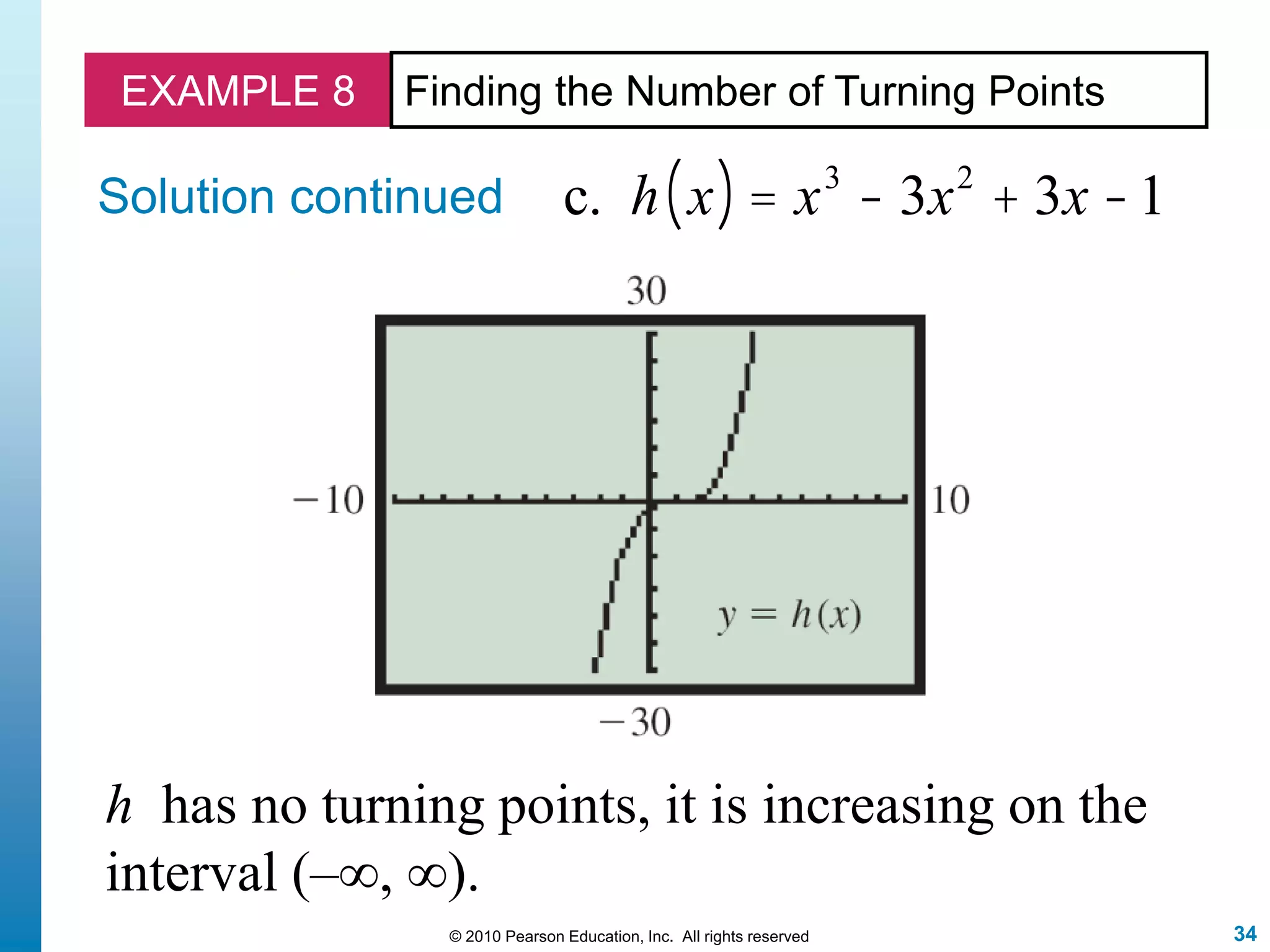
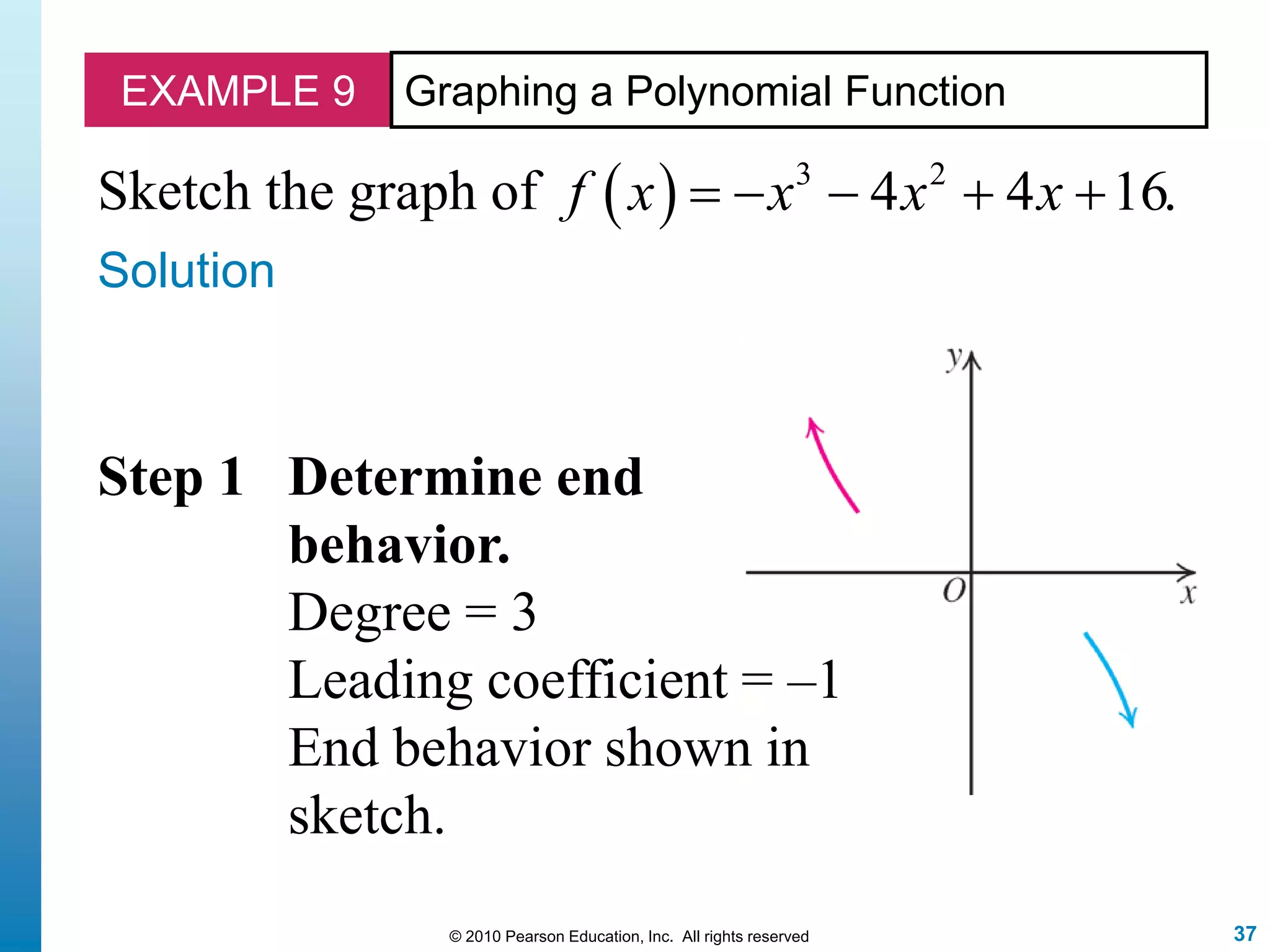
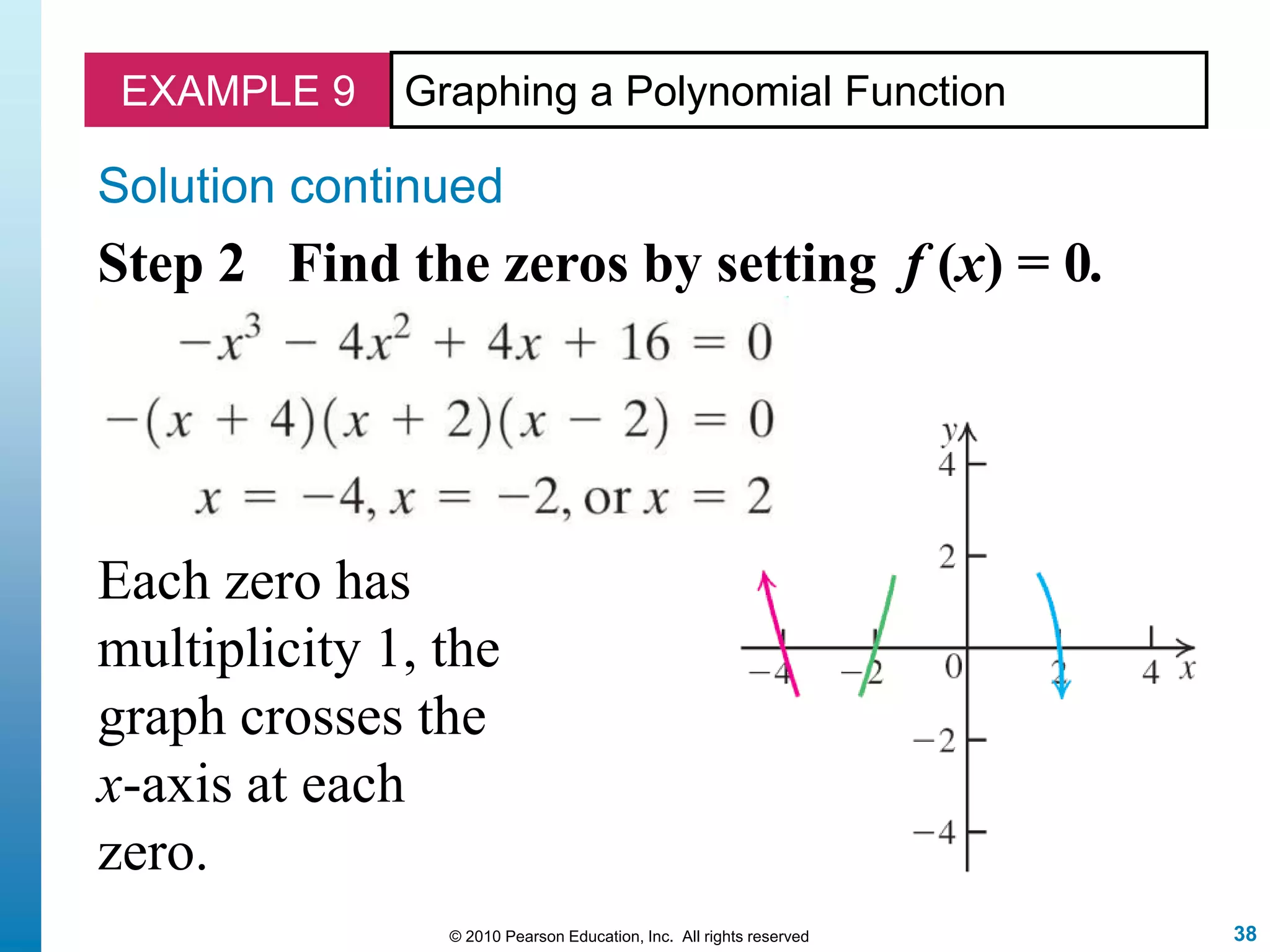
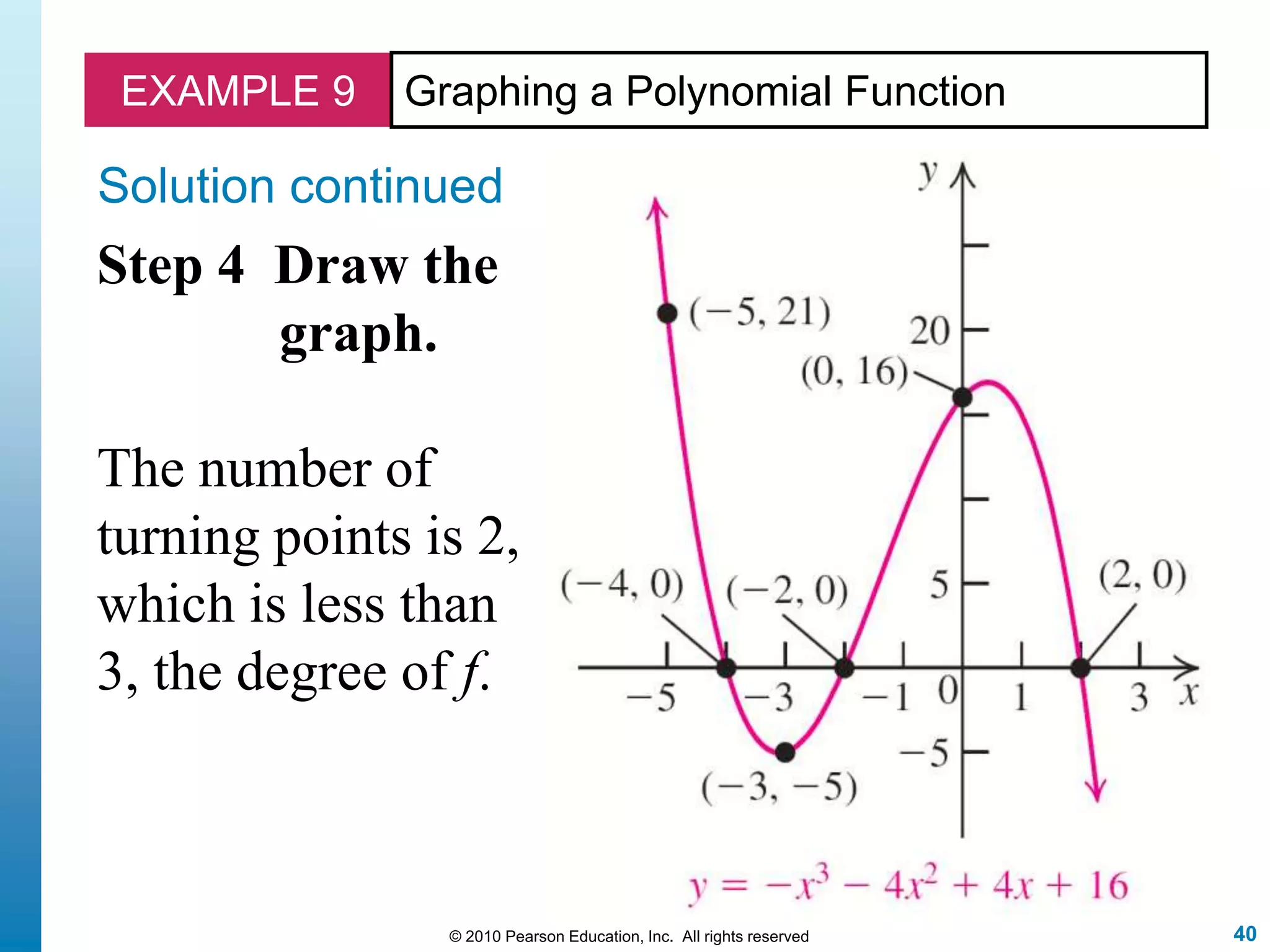
This document discusses polynomial functions. It defines polynomial functions as functions of the form f(x) = anx^n + an-1x^(n-1) + ... + a1x + a0, where n is a nonnegative integer and the coefficients are real numbers. It discusses key properties of polynomial functions including their domain, continuity, end behavior determined by the leading term, real zeros, turning points, and graphing. The document provides examples illustrating these concepts.