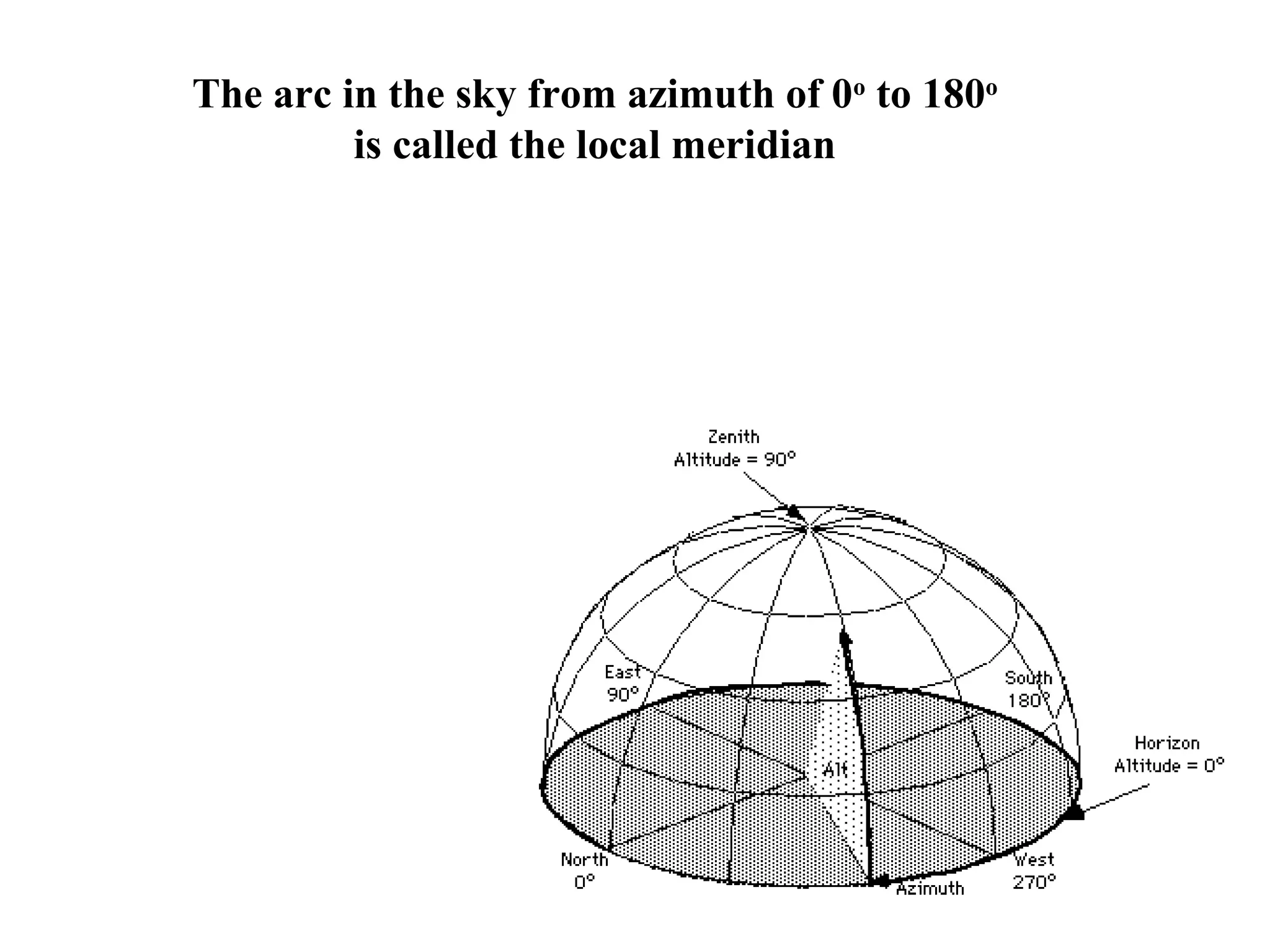
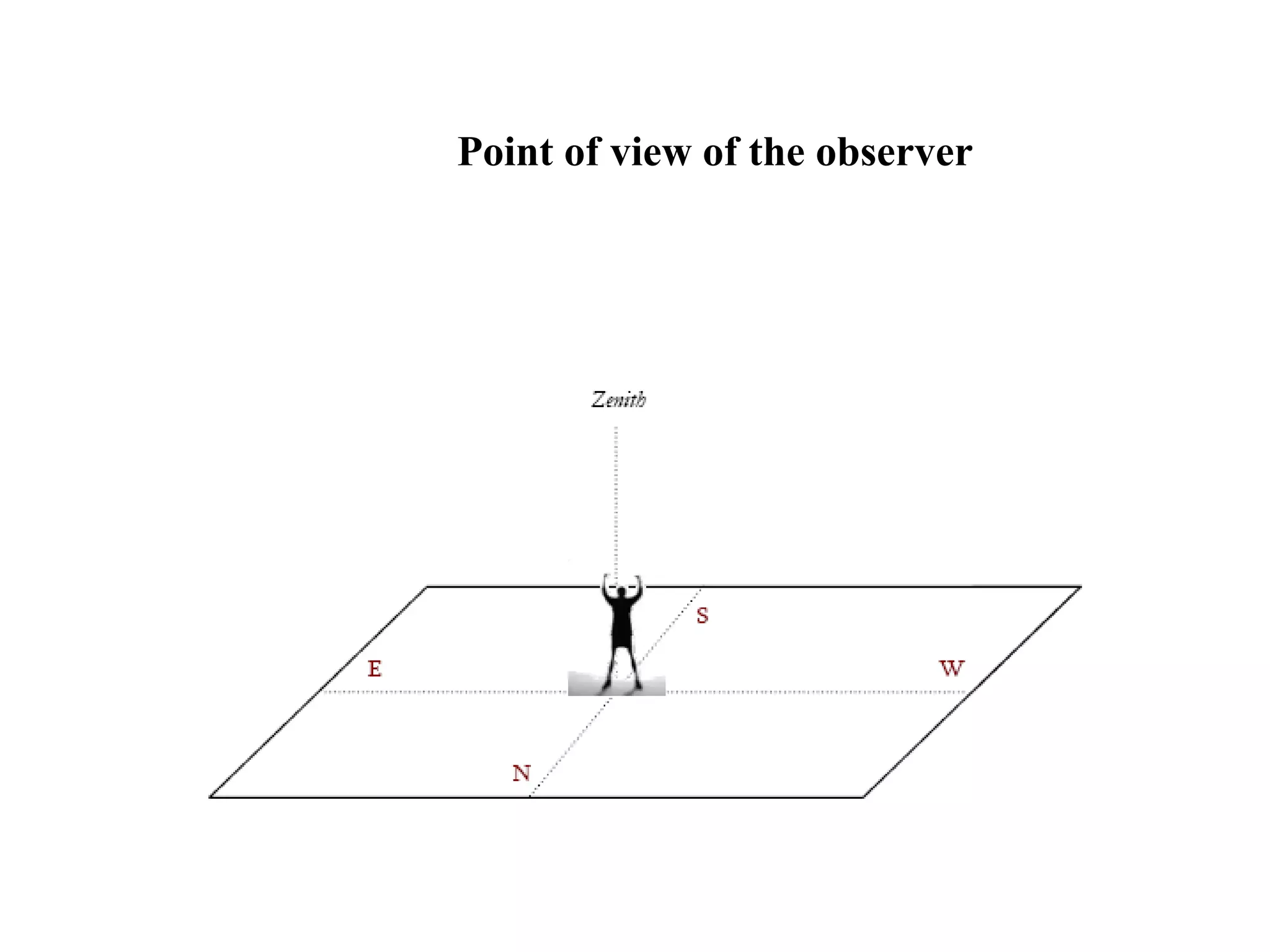
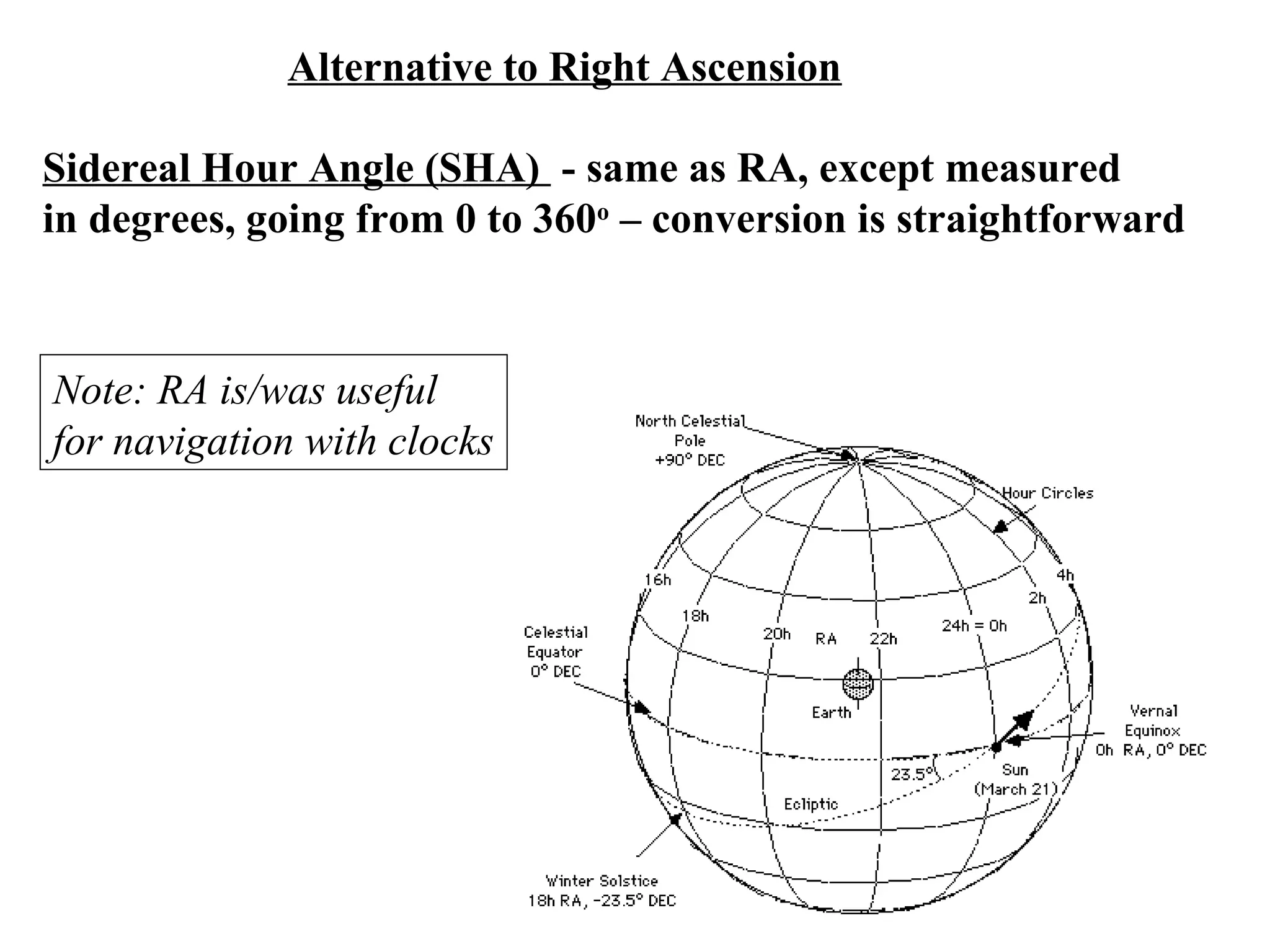
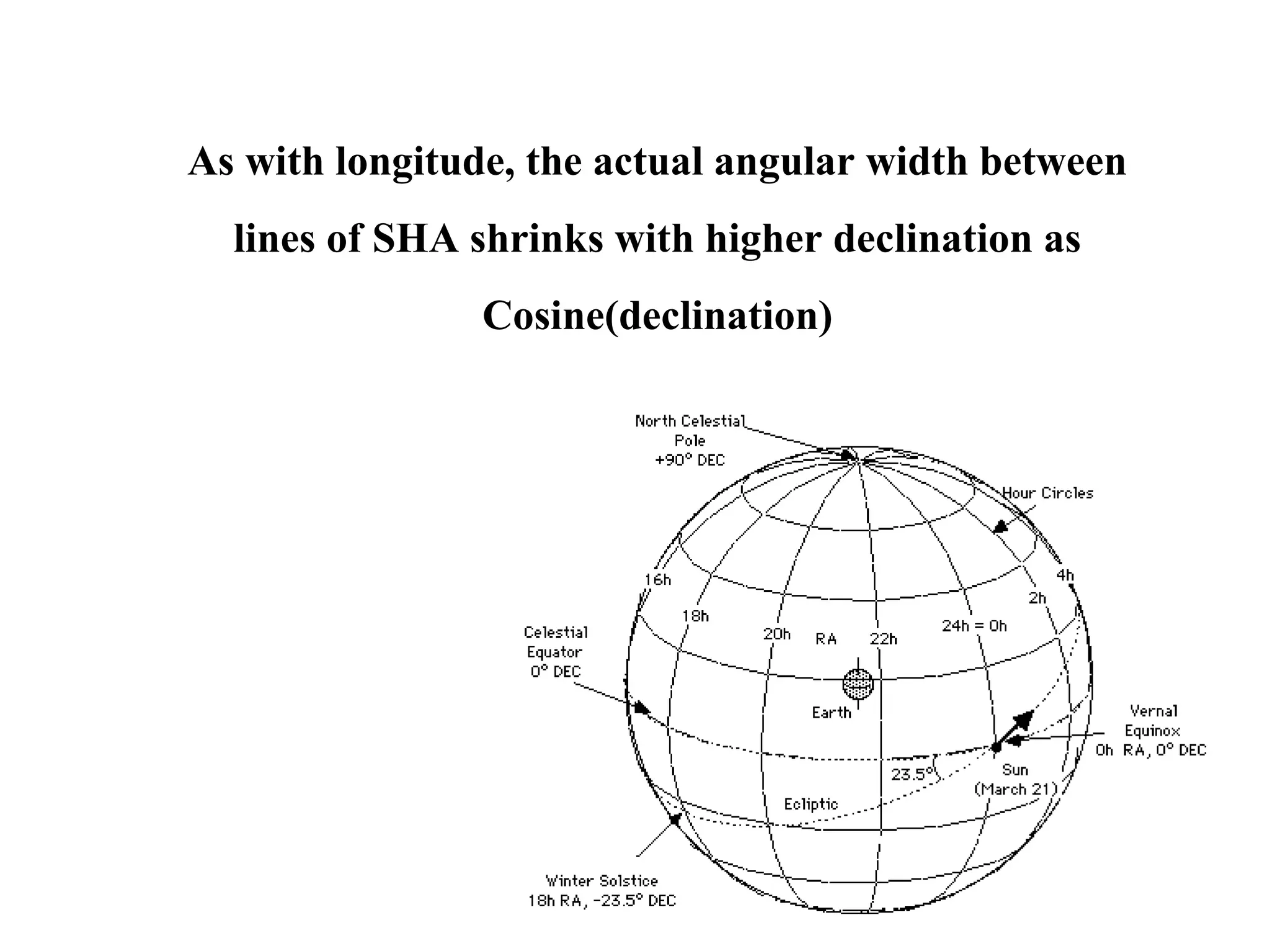
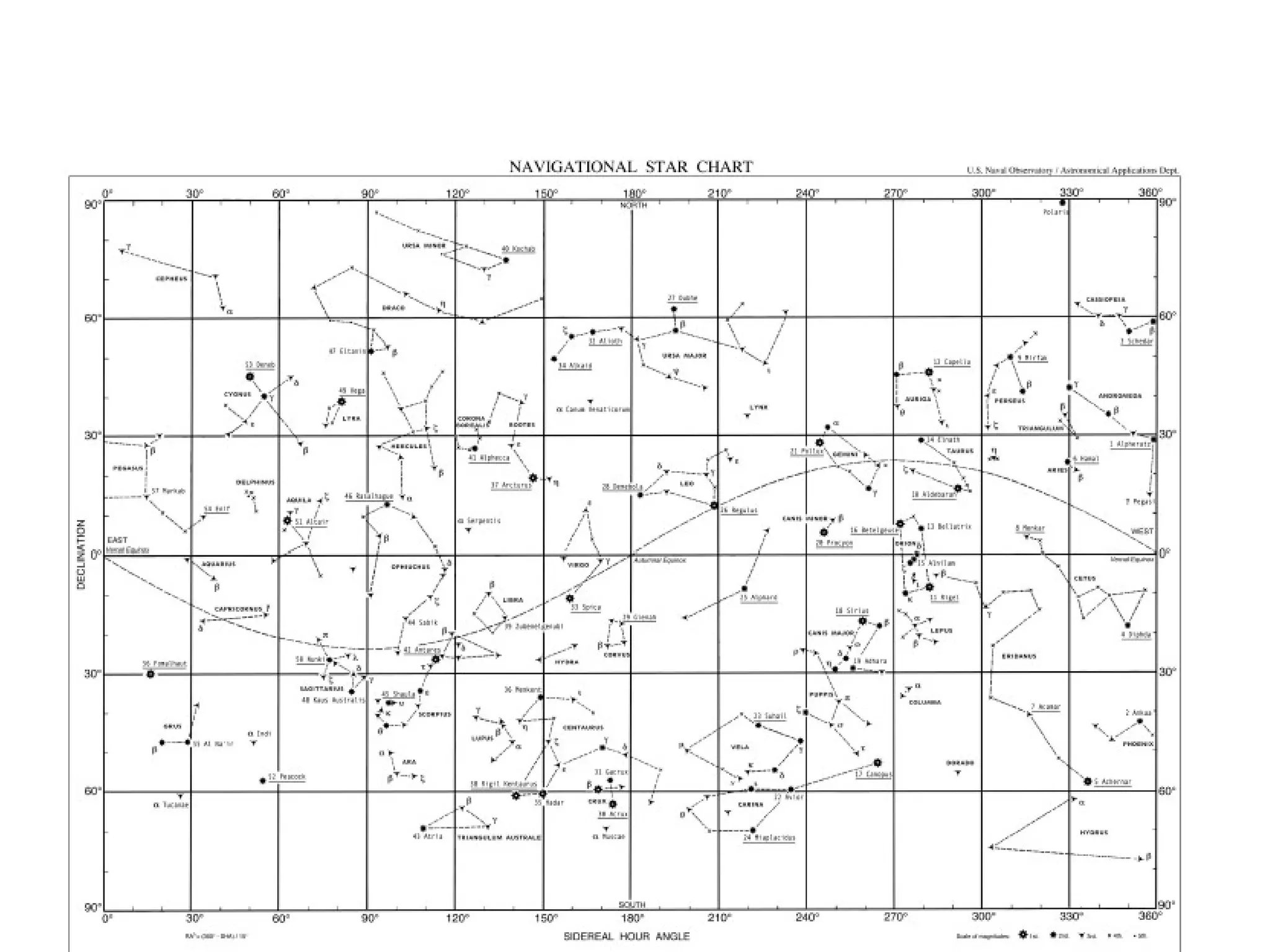
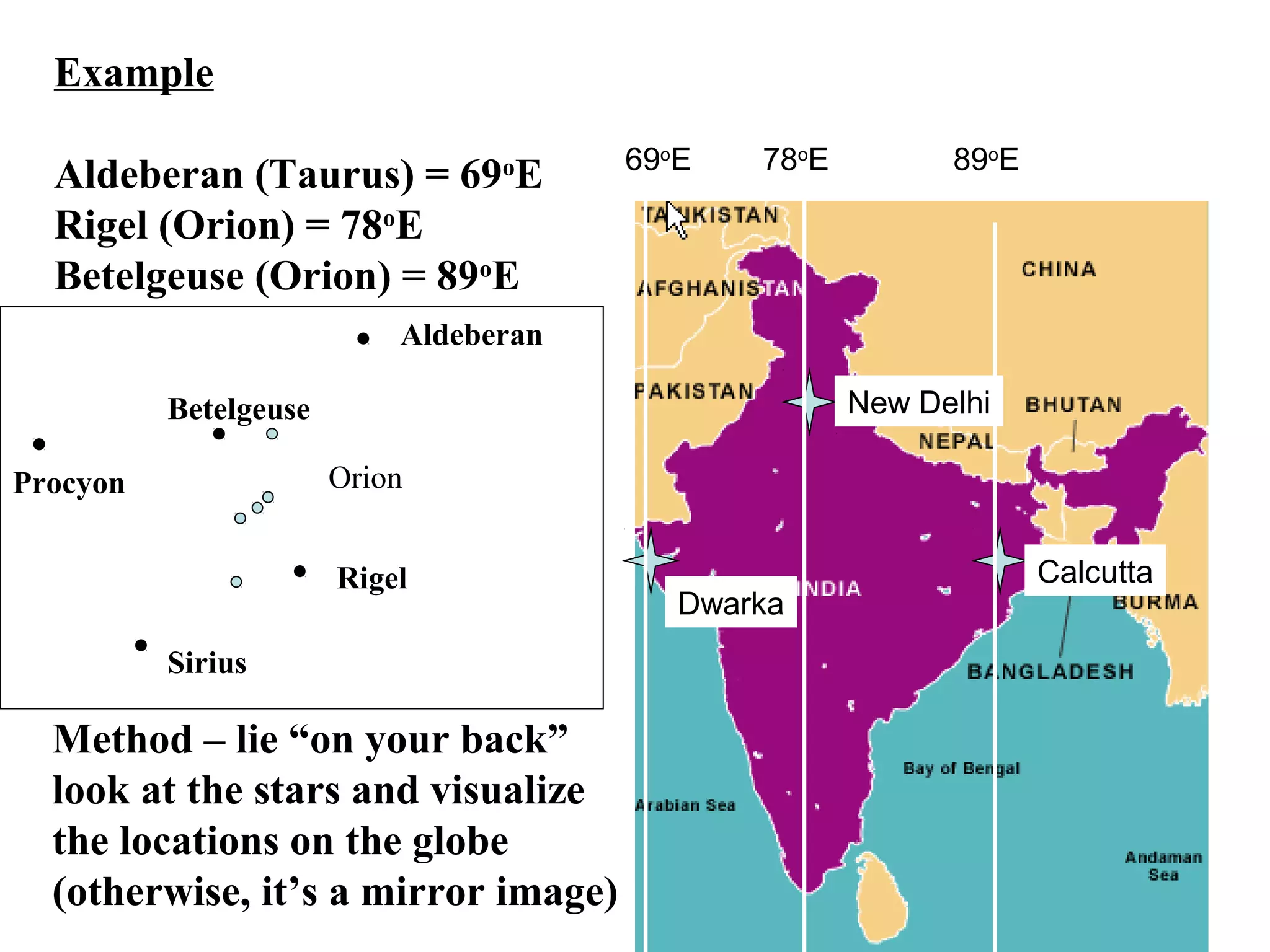
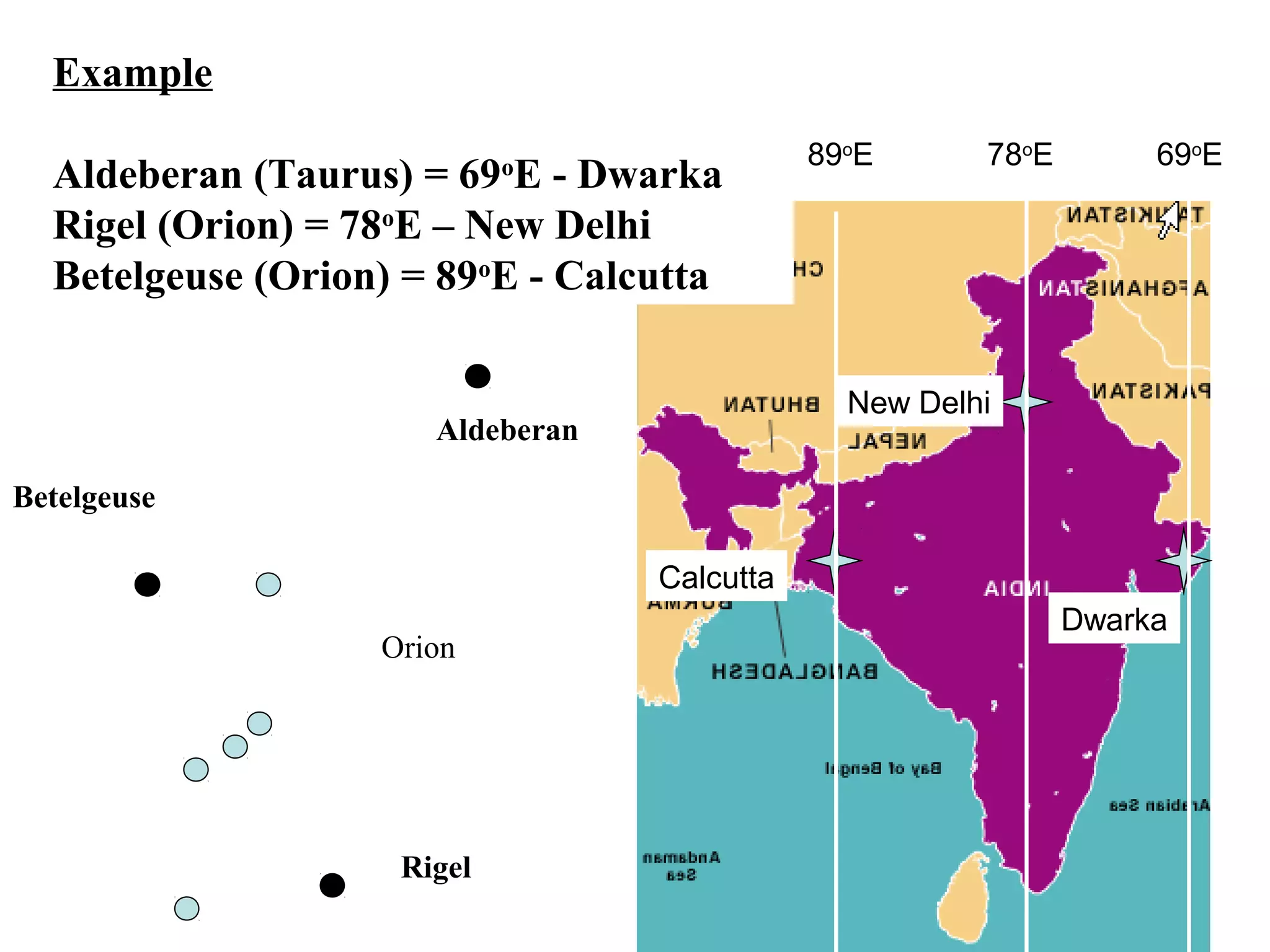
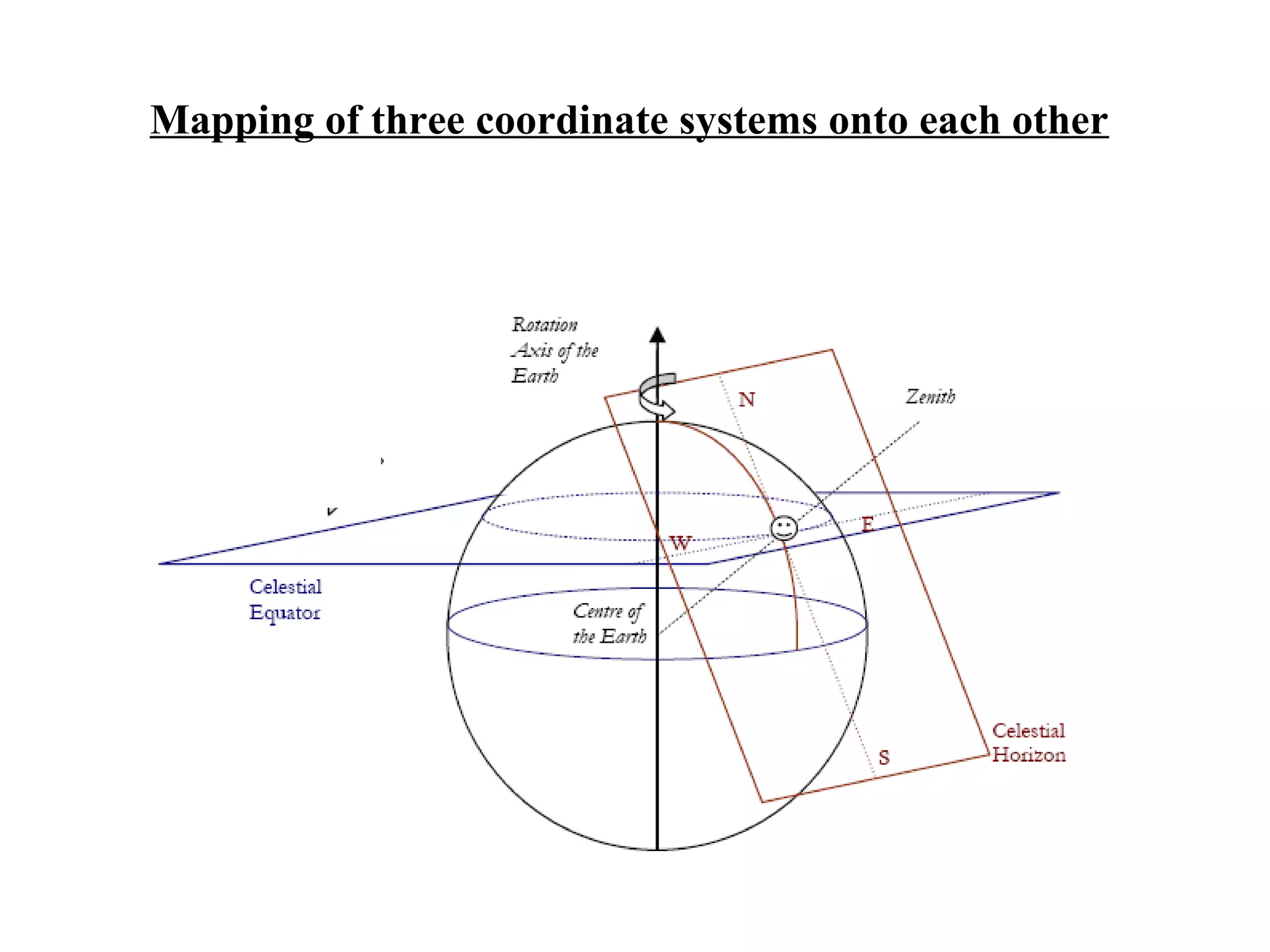
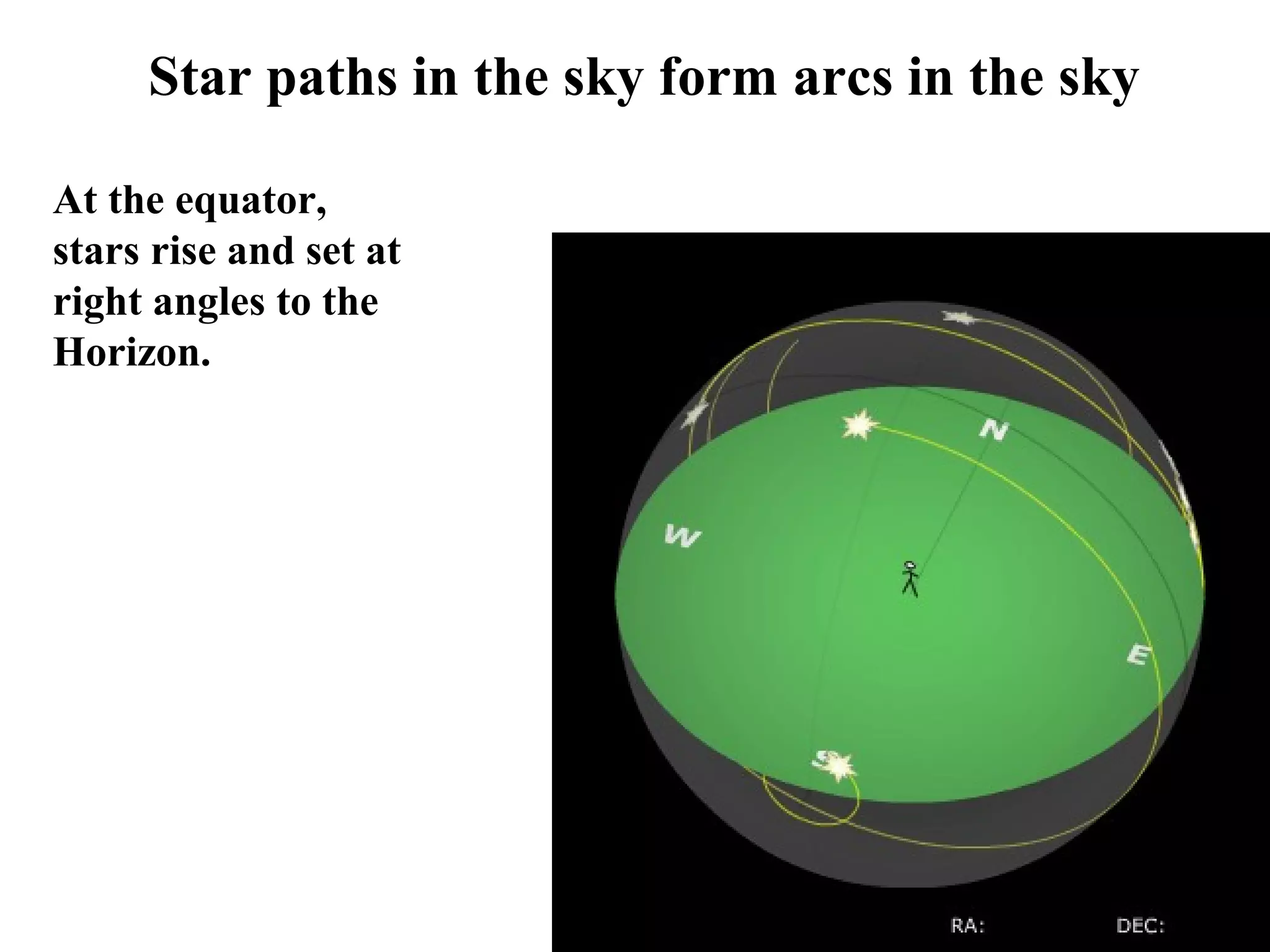
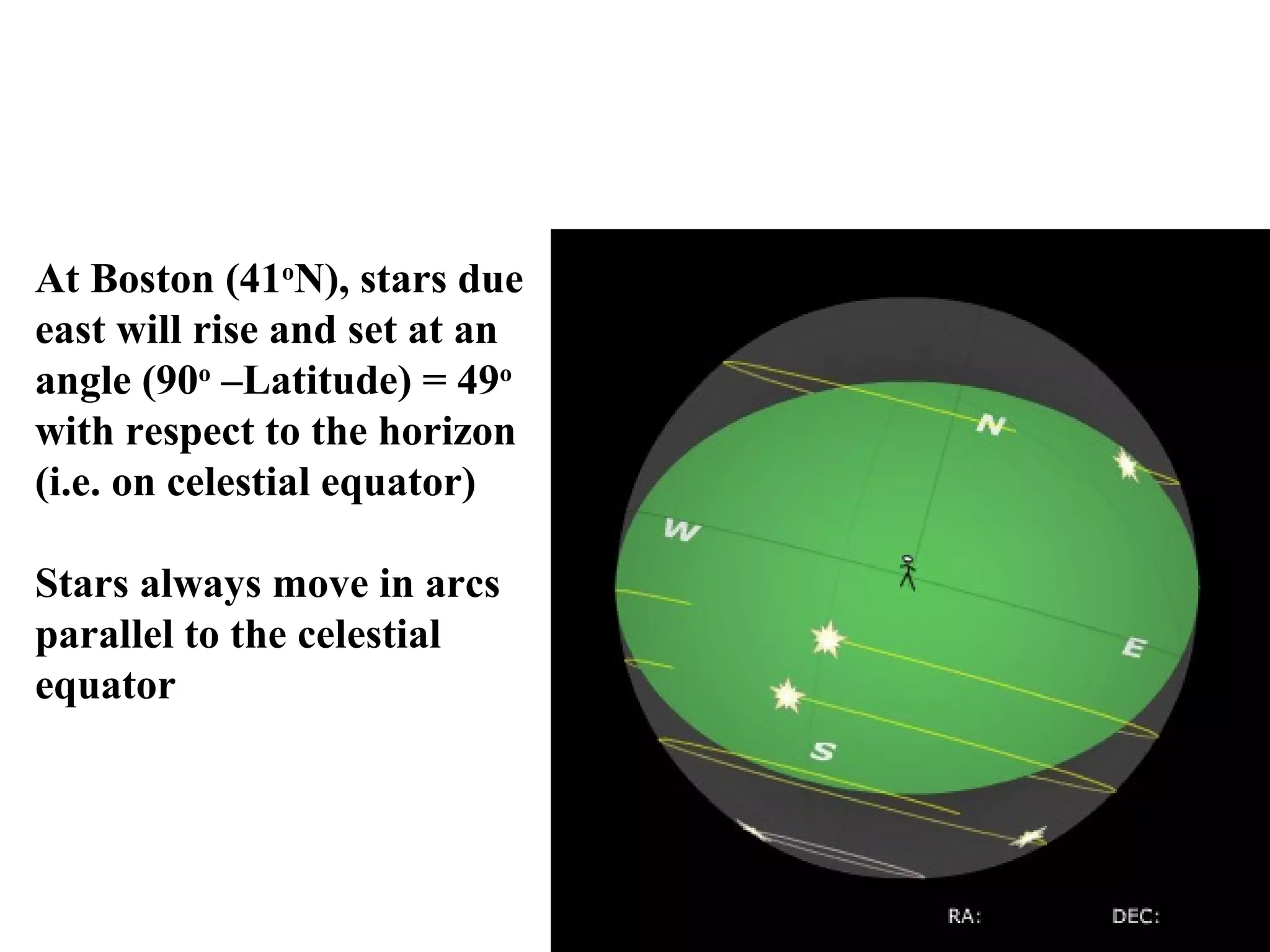
The document discusses coordinate systems used in celestial navigation including altitude-azimuth, latitude-longitude on Earth, and declination-right ascension in the sky. It explains how the three systems relate and how celestial objects move relative to observers on Earth. Major star groupings are described that can help navigators identify locations, including the Big Dipper, Summer Triangle, Orion, and winter constellations like Gemini and Leo. Specific stars are given for each constellation with their declinations and right ascensions or stellar longitudes to allow plotting positions.

1. Basics of Celestial Navigation -
stars
• Coordinate systems
– Observer based – azimuth and altitude
– Earth based – latitude and longitude
– Celestial – declination and right ascension (or
sidereal hour angle)
• Relationship among three – star pillars
• Motions of the stars in the sky
• Major star groupings

2. Comments on coordinate systems
• All three are basically ways of describing locations on a
sphere – inherently two dimensional
– Requires two parameters (e.g. latitude and longitude)
• Reality – three dimensionality
– Height of observer
– Oblateness of earth, mountains
– Stars at different distances (parallax)
• What you see in the sky depends on
– Date of year
– Time
– Latitude
– Longitude
– Which is how we can use the stars to navigate!!

3. Altitude-Azimuth coordinate system
Based on what an observer sees in the sky.
Zenith = point directly above the observer (90o
)
Nadir = point directly below the observer (-90o
) – can’t be seen
Horizon = plane (0o
)
Altitude = angle above the horizon to an object (star, sun, etc)
(range = 0o
to 90o
)
Azimuth = angle from
true north (clockwise)
to the perpendicular arc
from star to horizon
(range = 0o
to 360o
)
Note: lines of azimuth
converge at zenith

4. The arc in the sky from azimuth of 0o
to 180o
is called the local meridian

5. Point of view of the observer

6. Latitude
Latitude – angle from the equator (0o
) north (positive) or
south (negative) to a point on the earth – (range = 90o
= north
pole to – 90o
= south pole). 1 minute of latitude is always =
1 nautical mile (1.151 statute miles)
Note: It’s more
common to express
Latitude as 26o
S or
42o
N

7. Longitude
Longitude = angle from the prime meridian (=0o
) parallel
to the equator to a point on earth (range = -180o
to 0 to
+180o
) East of PM = positive, West of PM is negative.
Distance between lines of longitude depend on latitude!!
Note: sometimes
positive longitude
is expressed as
West, but this is
inconsistent with
math conventions.
Avoid confusion:
40o
W or 40o
E

8. Comments on longitude
Location of prime meridian is arbitrary = Greenwich
observatory in UK
1 minute of longitude = 1 nautical mile * cosine(latitude)
Lines of longitude converge at the north and south poles
To find longitude typically requires a clock, although there
is a technique, called the lunar method that relies on the fact
that the moon moves ½ of a degree per hour.

9. Celestial coordinates - some definitions
North celestial pole = point in sky directly above north pole
on earth (i.e. zenith of north pole)
South celestial pole = zenith of south pole on earth
Celestial equator – circle
surrounding equator on earth
Ecliptic – path followed
by the sun through the
sky over the course of
the year against a
“fixed” background of
stars

10. Declination – angle from celestial equator (=0o
), positive
going north (north celestial pole = + 90o
), negative going
south (south celestial pole = - 90o
)
Right ascension (RA) – angle from celestial “prime meridian” –
equivalent of celestial longitude
RA – typically expressed
as a time going east – 0 to
24 hours is 360o
“Prime meridian” – point
where sun is located at
the vernal equinox (spring)
(called vernal equinoctial
colure)

11. Declination and “star pillars”
Declination “maps” onto latitude –
At some point a star of a given
declination will pass over the zenith
at a point on the earth at its corresponding latitude.
This happens once every
24 hours

12. Alternative to Right Ascension
Sidereal Hour Angle (SHA) - same as RA, except measured
in degrees, going from 0 to 360o
– conversion is straightforward
Note: RA is/was useful
for navigation with clocks

13. As with longitude, the actual angular width between
lines of SHA shrinks with higher declination as
Cosine(declination)

15. John Huth’s alternative to SHA, RA
Use same convention as for terrestrial longitude, with
positive and negative angles. Prime meridian corresponds
to 0o
for SHA
Same as SHA for 0o
to 180o
and (360o
– SHA) for values
of SHA from 180o
to 360o
Why? Easy to remember,
and allows you to associate
star coordinates with points
on earth. Makes it easier to
visualize and memorize.
Also – declination and latitude
go together.

16. New Delhi
Calcutta
Dwarka
69o
E 78o
E 89o
E
Example
Aldeberan (Taurus) = 69o
E
Rigel (Orion) = 78o
E
Betelgeuse (Orion) = 89o
E
Aldeberan
Betelgeuse
Rigel
Sirius
Procyon Orion
Method – lie “on your back”
look at the stars and visualize
the locations on the globe
(otherwise, it’s a mirror image)

17. Dwarka
New Delhi
Calcutta
69o
E78o
E89o
E
Aldeberan
Betelgeuse
Rigel
Orion
Example
Aldeberan (Taurus) = 69o
E - Dwarka
Rigel (Orion) = 78o
E – New Delhi
Betelgeuse (Orion) = 89o
E - Calcutta

18. Can associate star coordinates with latitude and
Longitude of locations on earth
Note: don’t expect alignment with any star – this is just
a way to memorize coordinates

19. Important Point
• Mariners had to/have to rely on tables for
star coordinates
• You can memorize major navigational star
coordinates and eliminate tables
• Helps identify stars, too
• On a desert island, with only a watch, can
identify latitude and longitude – along with
your memory!
• Tell that to the creators of “Lost”!!

20. Mapping of three coordinate systems onto each other

21. How stars move through the sky
• Stars move in arcs that parallel the
celestial equator – angle perpendicular to
celestial equator is the declination
• Star move across the sky at 15o
per hour
(4 minutes per degree)
• Each day star positions move 1o
west
• Stars on the celestial equator rise and set
with angles of (90o
– Latitude)
• Some stars are “circumpolar” – never set

22. Star paths in the sky form arcs in the sky
At the equator,
stars rise and set at
right angles to the
Horizon.

23. At Boston (41o
N), stars due
east will rise and set at an
angle (90o
–Latitude) = 49o
with respect to the horizon
(i.e. on celestial equator)
Stars always move in arcs
parallel to the celestial
equator

24. Paths of stars as seen
from the N. Arctic Circle
66o
N – few stars rise and
set – most make complete
circles

25. θ
Rising/setting angle is (90o
– Latitude) due
east/west – along celestial equator
Angles are smaller the further N/S one goes

26. Relation between Azimuth, Latitude and Declination of
rising and setting stars
)cos(
)sin(
)cos(
L
d
Rz =
Where Rz = rising azimuth
d = declination
L = Latitude
So – at equator, L=0, cos(L) = 1, rising azimuth is the
declination of the star – exploited by Polynesians in
star compasses (near the equator cos(L) close to 1
Can use this to find latitude, if you’re willing to do the
math, and find the azimuth of a rising star, knowing
the star’s declination.

27. Notes on azimuth – when )cos()sin( Ld >
Then star is either circumpolar or below the horizon
Example – at latitude 45o
N, cos(L)=0.707, the star
Capella (declination = 46o
) just becomes circumpolar
Then cos(Rz) is just slightly greater than 1.
Largest rising/setting angles for Rz = 90/270 degrees
(along celestial equator)

28. Circumpolar stars – never set

29. Knowing a star’s declination, can get latitude
from horizon grazing stars.
Horizon (est)
Min. star height
Polar distance =
(90o
– Declination)
Latitude = (polar distance – minimum height)

30. Some star groupings
• If you can locate stars and know the
declination you can find your latitude.
• With a watch, and SHA (or “stellar
longitude”), you can find your longitude
(must know date).
• Clustering into constellations and their
stories help locate stars by name.

31. Big dipper
Arcturus
Spica
“Arc to Arcturus, spike to Spica”
After sunset:
Spring/summer
Arcturus (Decl = 19o
N)
and Spica (Decl = 11o
S)
“alone” in this part of
the sky (“longitude” =
146o
W and 159o
W
respectively)

32. Deneb Vega
Altair
Antares
Scorpio
Summer triangle and Antares
Antares is only
visible for a short
period (hours) in
mid summer.
Declination = 26o
S
Good candidate for a
horizon grazing star in
the summer

33. Altair
Vega
Deneb
Summer
Triangle
Cygnus/
Northern
Cross
Summer triangle, northern cross (Cygnus)
Vega (Decl = 39o
N) and Deneb (Decl = 45o
) straddle zenith
in Boston (Latitude = 42o
), Altair is 9o
N

34. Dubhe
Schedar
Cassiopeia
Big dipper/Ursa major
Polaris
Finding Polaris from the big dipper
Schedar (Decl = 56o
)
and Dubhe (Decl = 62o
)
are circumpolar for Boston
Also can be used as
the basis for a “clock”
(project)

35. Aldeberan
Betelgeuse
Rigel
Sirius
Procyon Orion
Constellation story about Orion
Pleiades
Winter constellations – Zeus’ daughters, Pleiades (24N, 57E)
are guarded by Taurus (Aldeberan = orange eye – 17N, 69E), from
Orion, the hunter (Betelgeuse = 7N, 89E, Rigel 8S,78E), followed
by hunting dogs Canis Minor (Procyon = 5N, 115E) and
Canis Major (Sirius = 17S and 101E)
Mintaka – right star
in belt is on the equator

36. Time lapse image of Orion
Sirius
Betelgeuse
Rigel
Arcturus

37. Regulus
Leo Pollux
Gemini
Procyon
Late winter/early spring constellations
Pollux/Procyon line (115E) forms good north-south arc
Pollux (28N, 115E) is readily recognized with twin Castor
Regulus (12N, 152E)
marks start of sparsely populated
region of stars in N. hemisphere –
closest is Arcturus (142W)