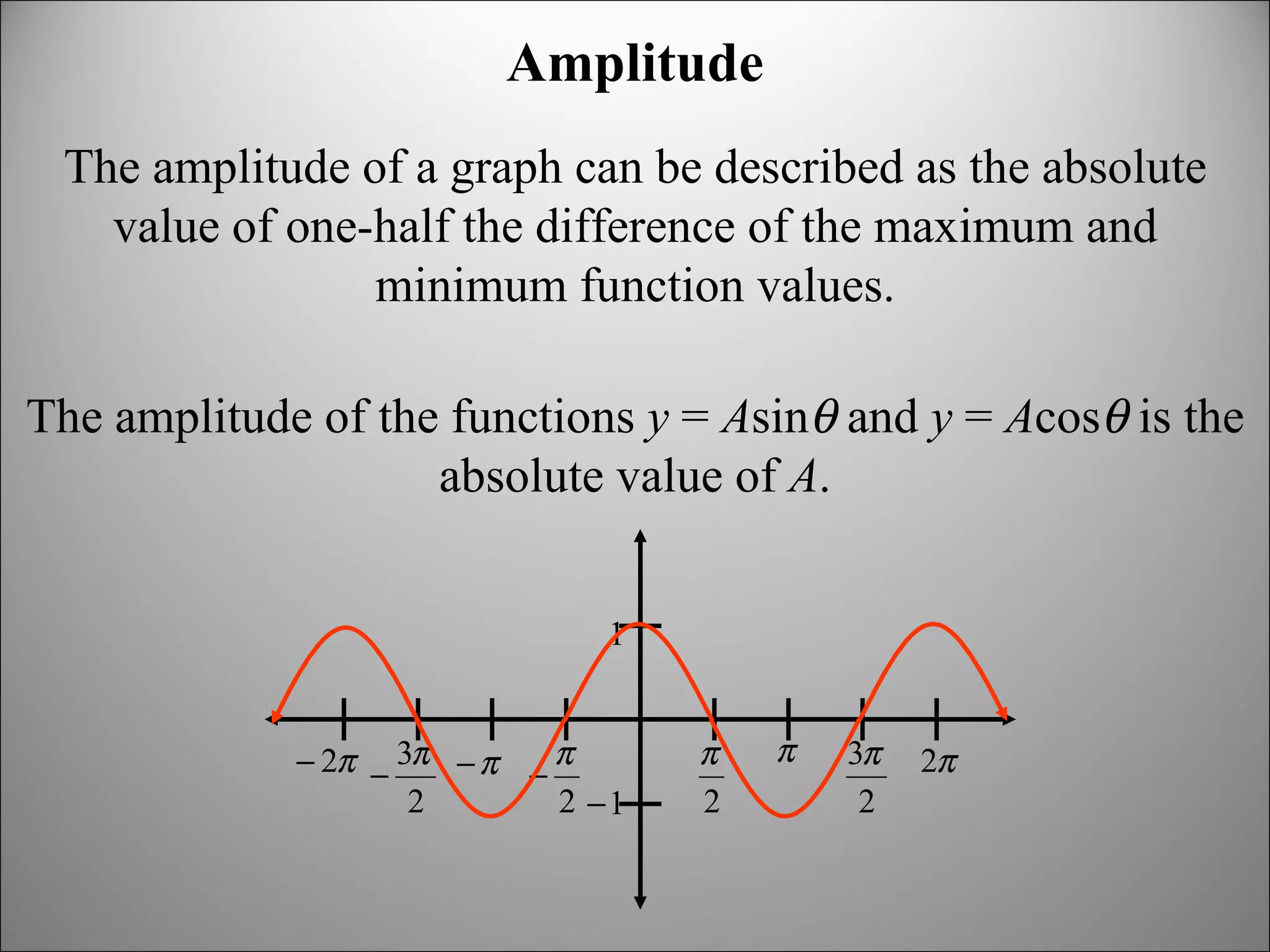
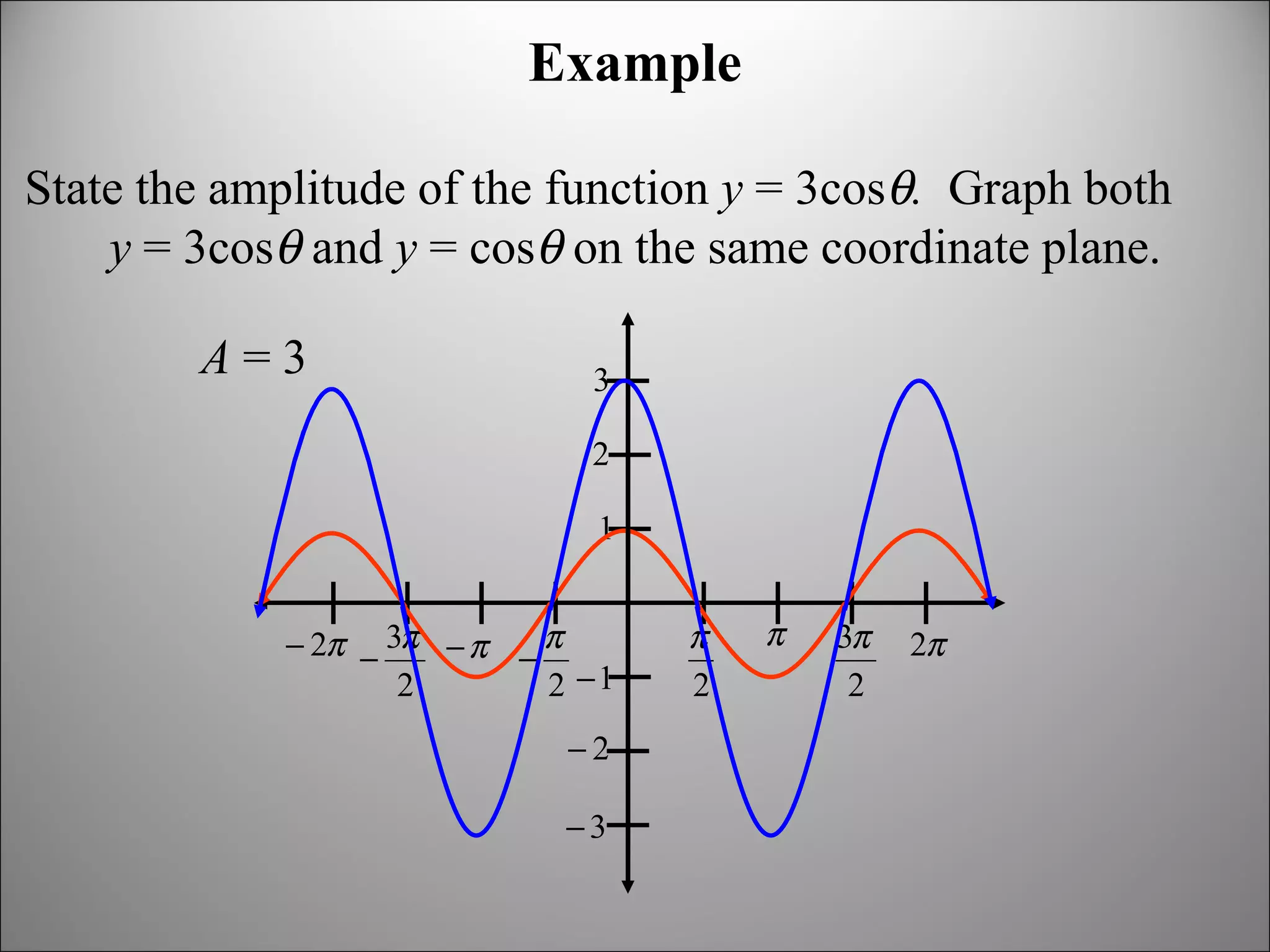
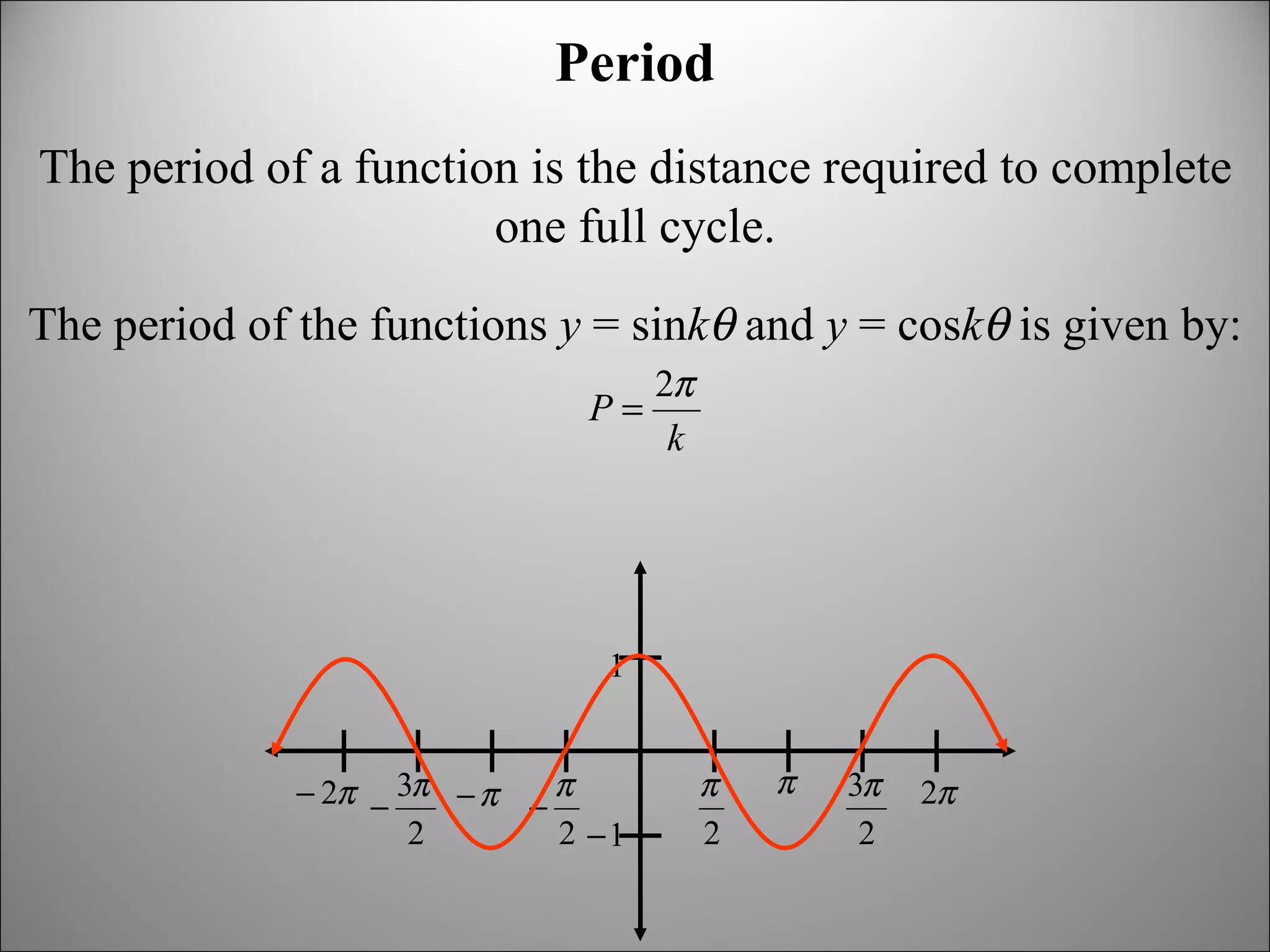
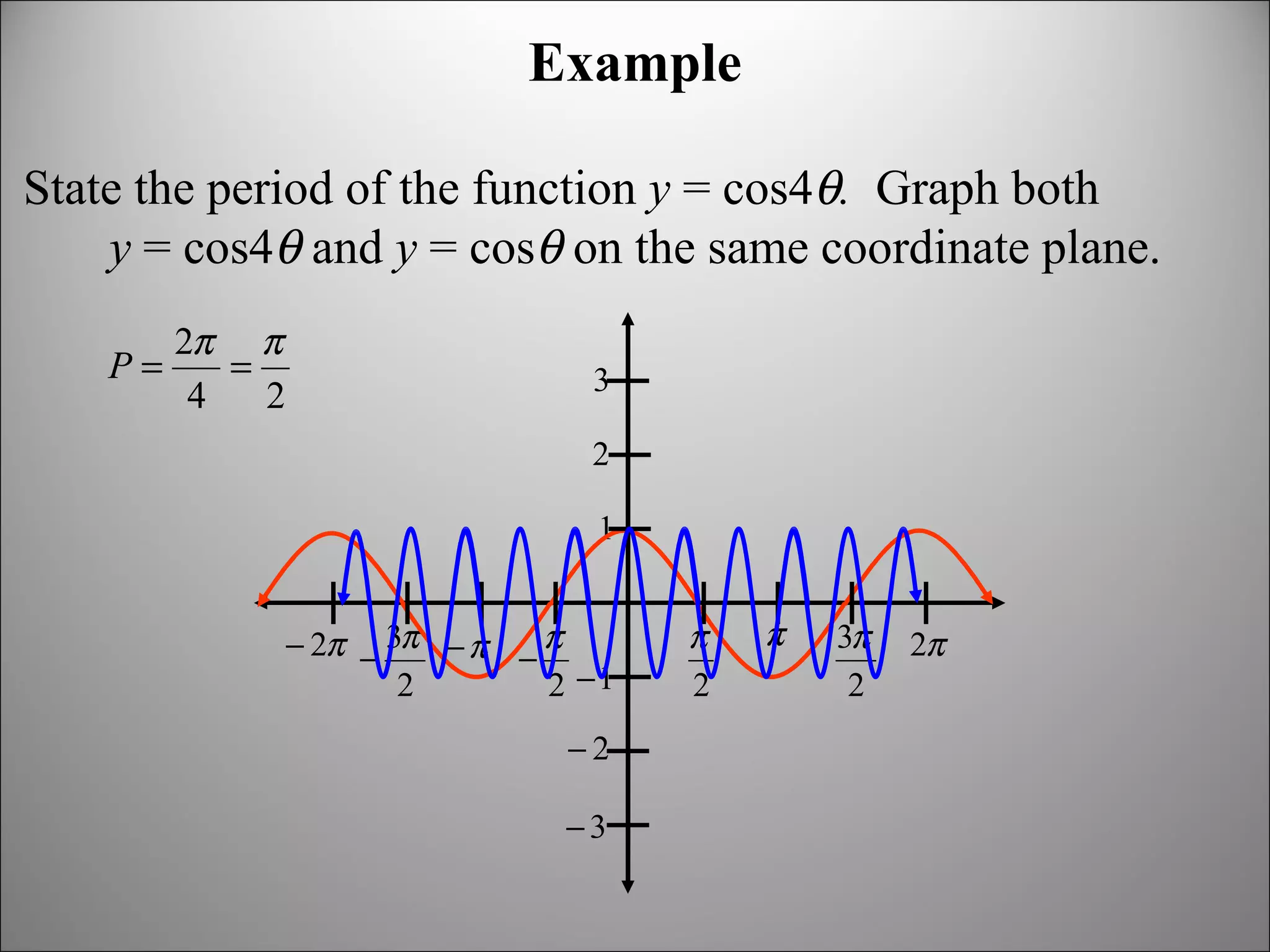
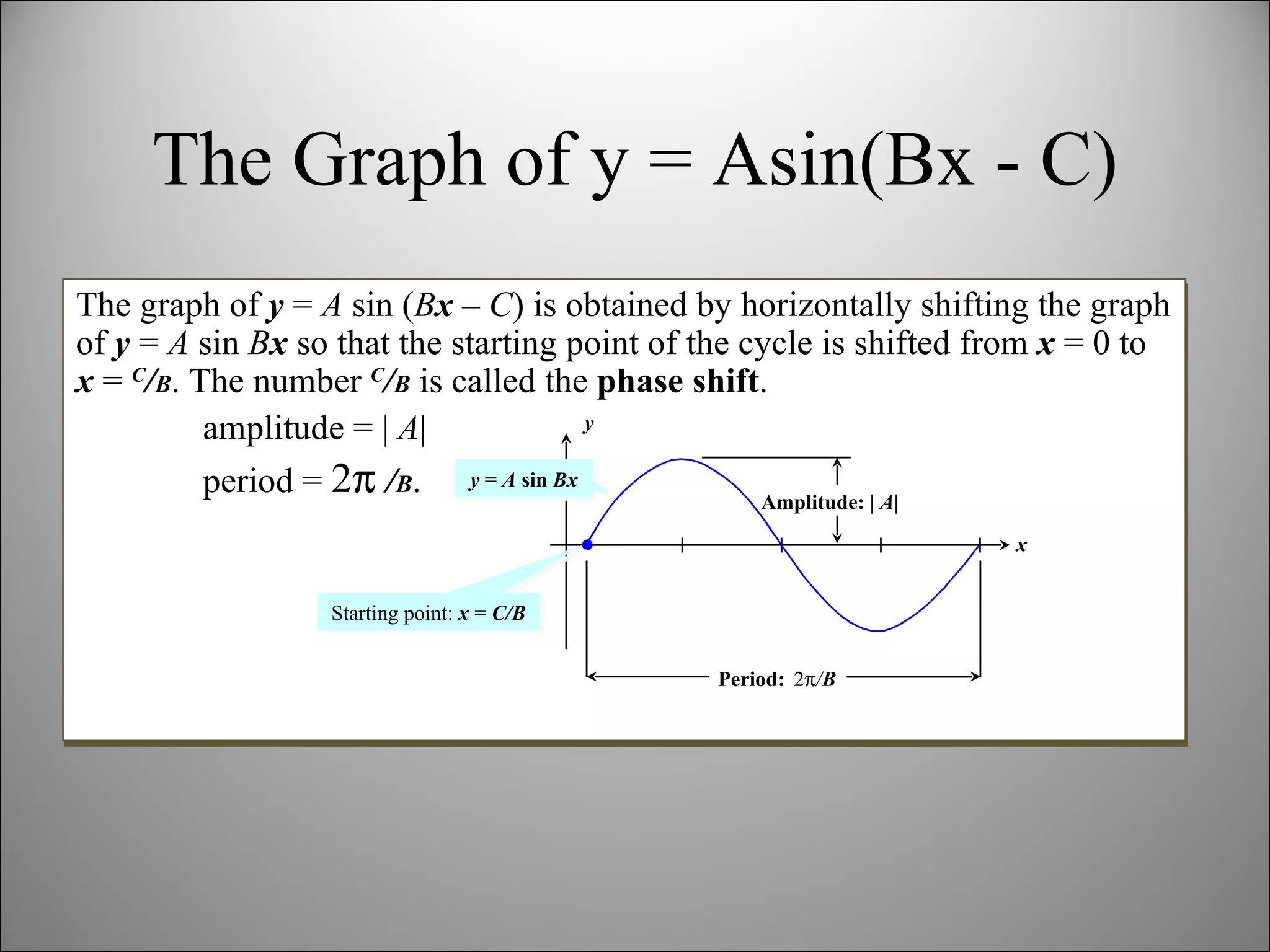
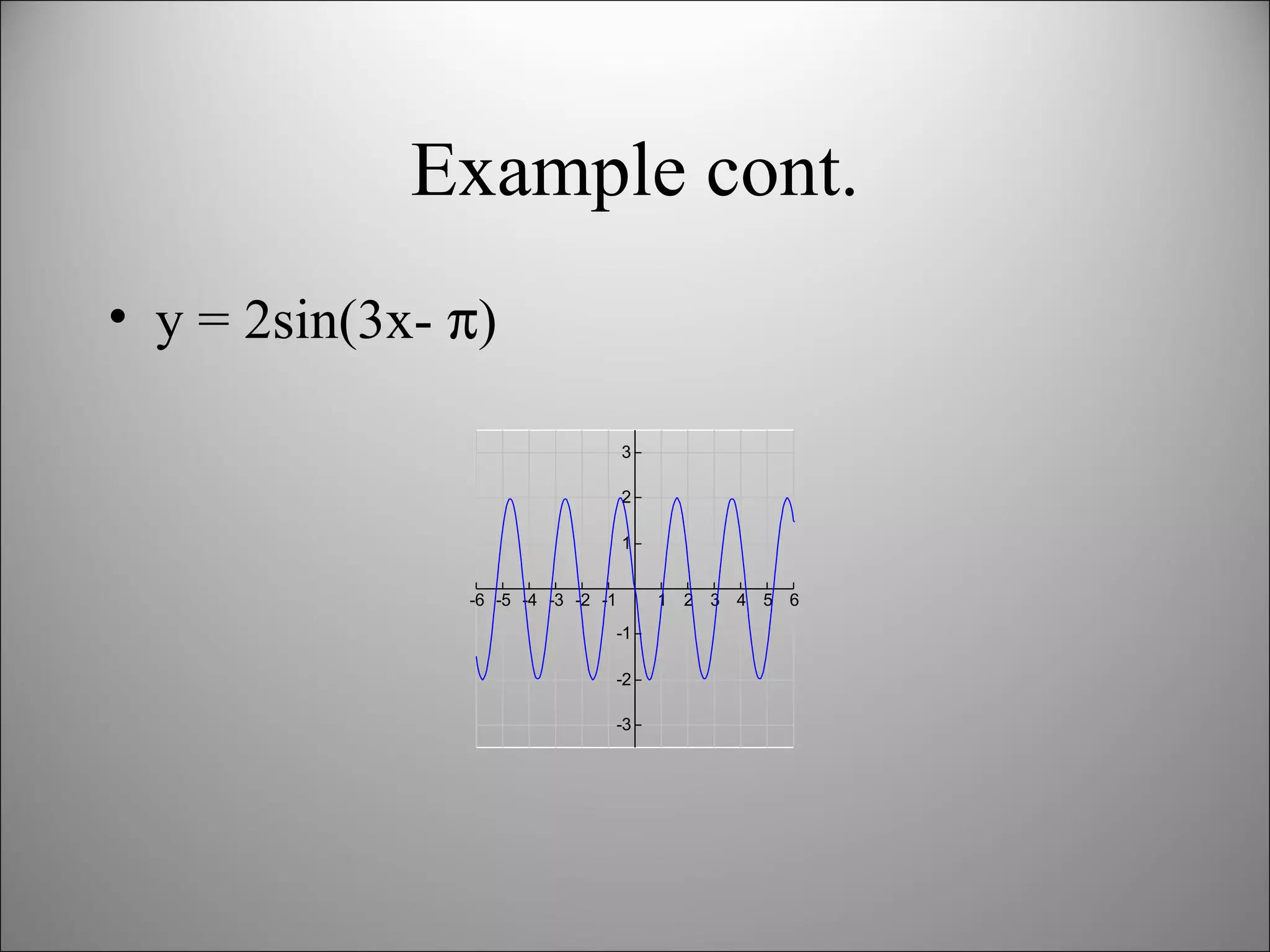
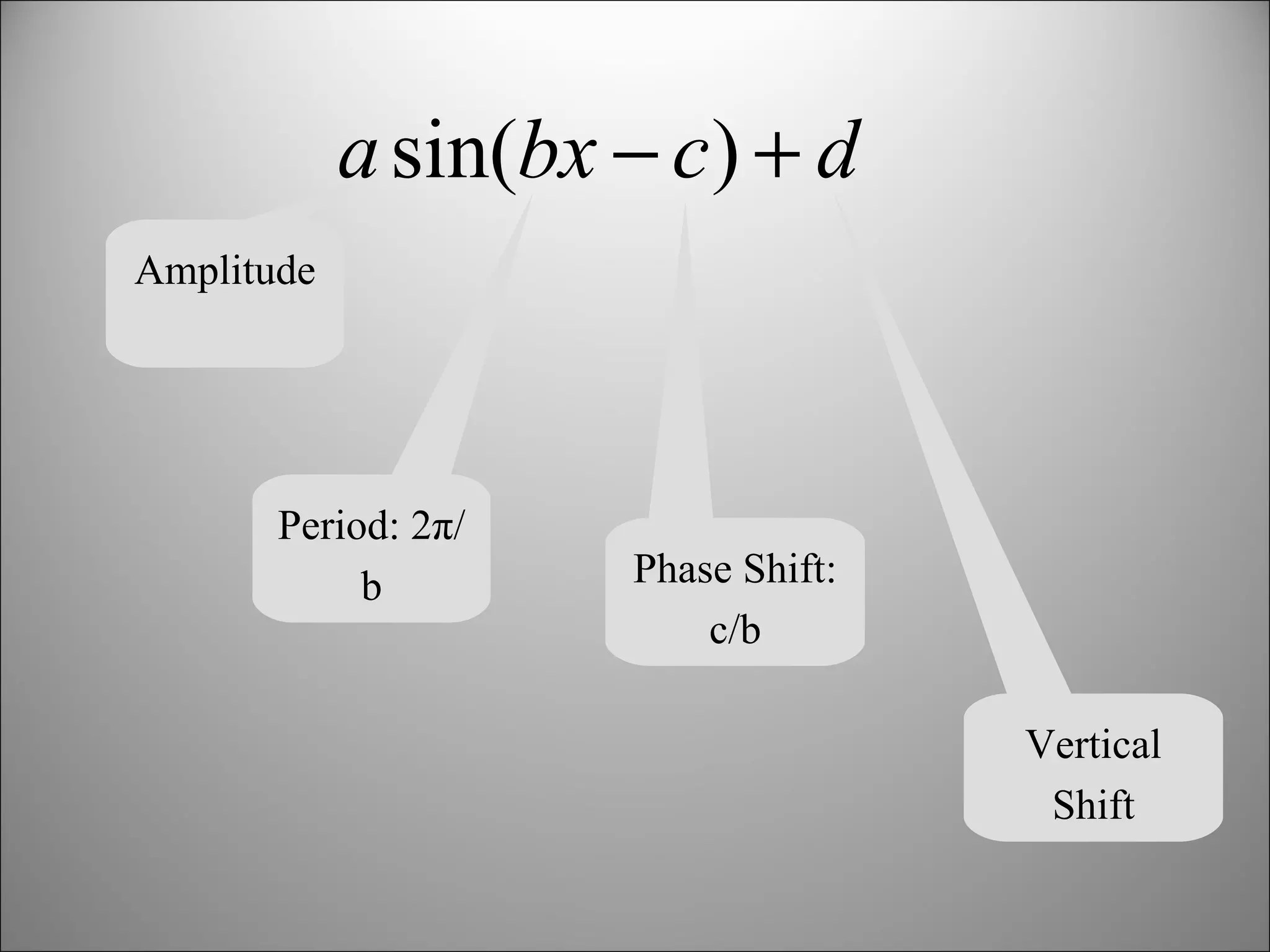
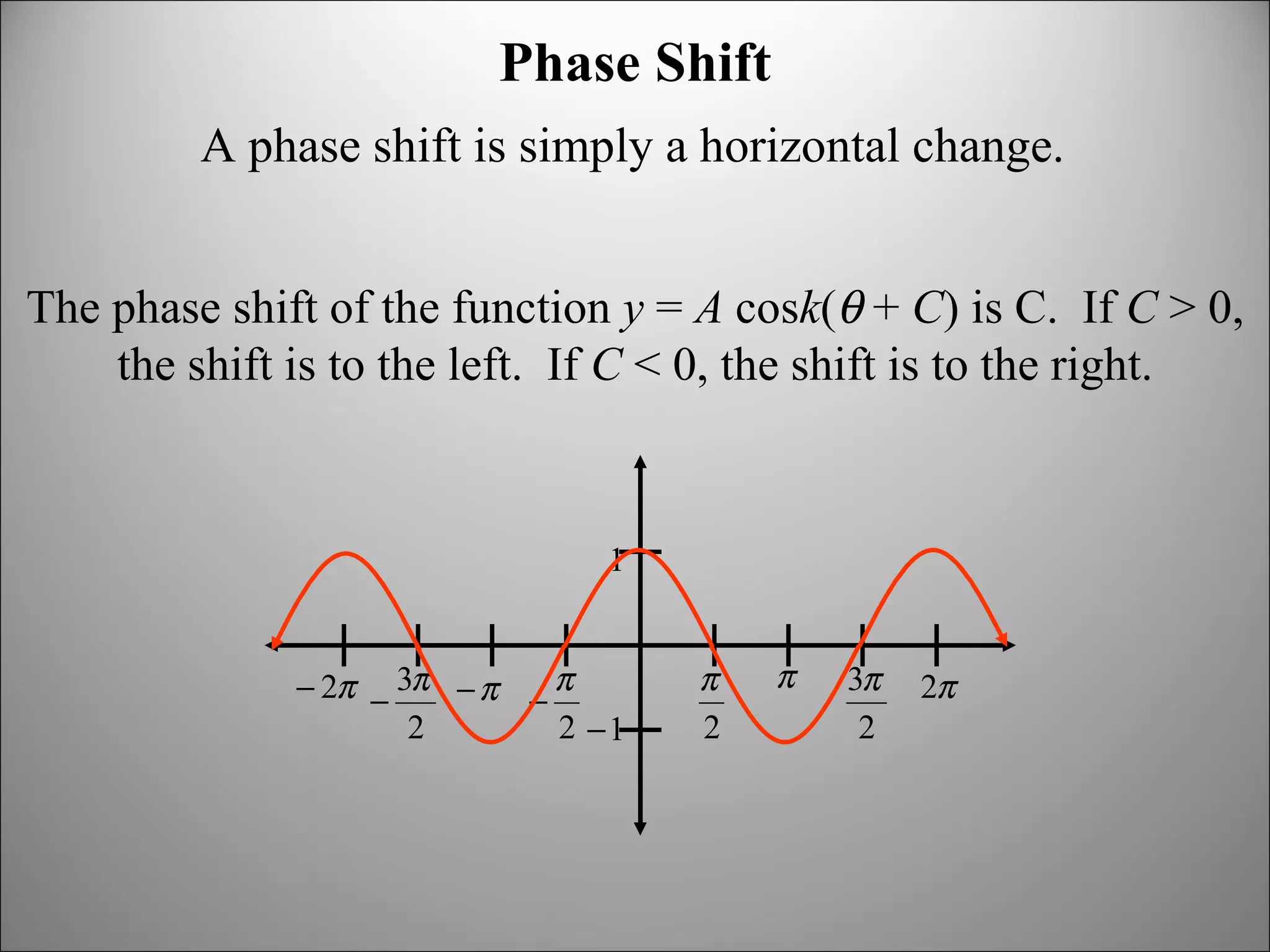
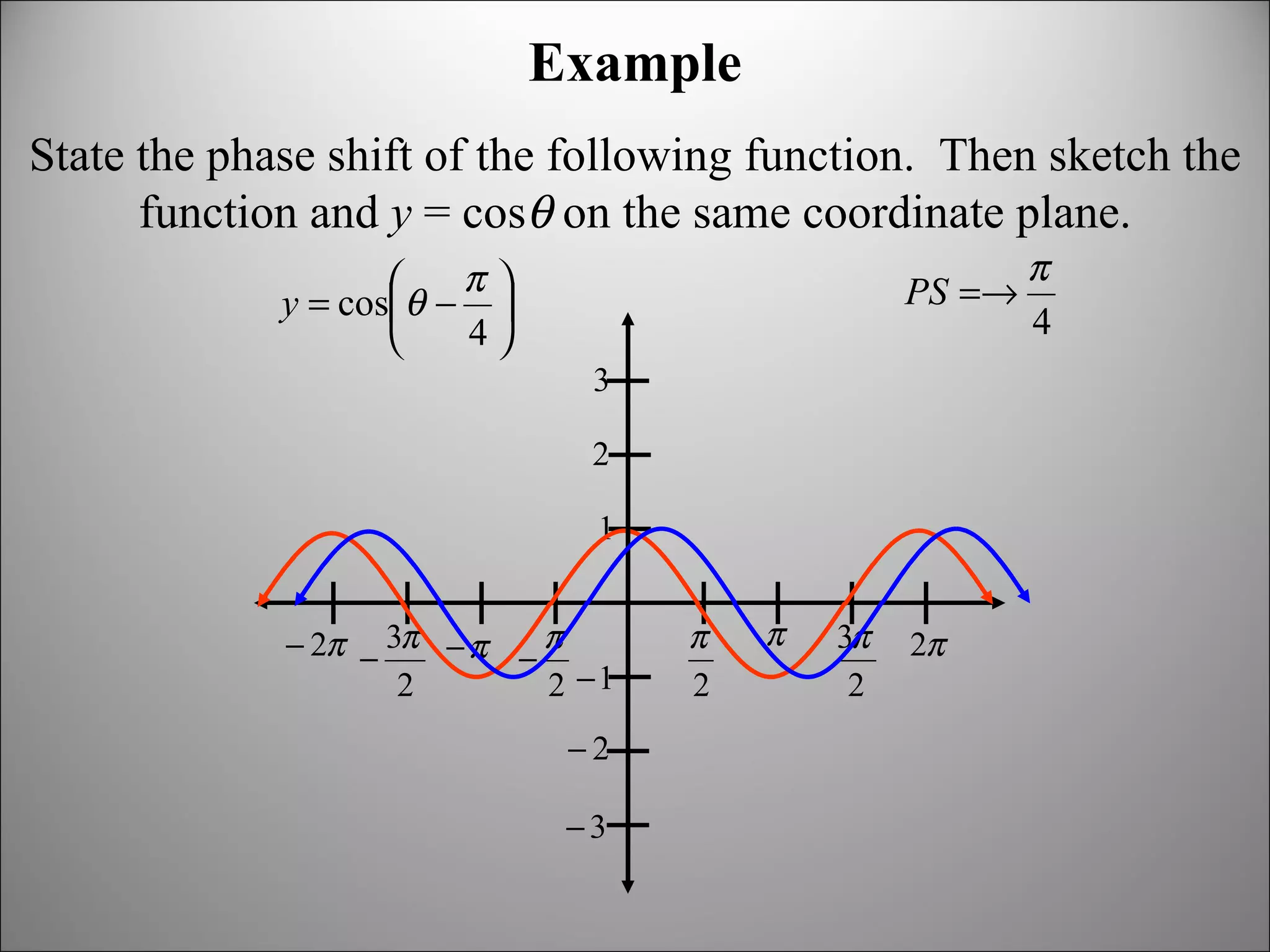
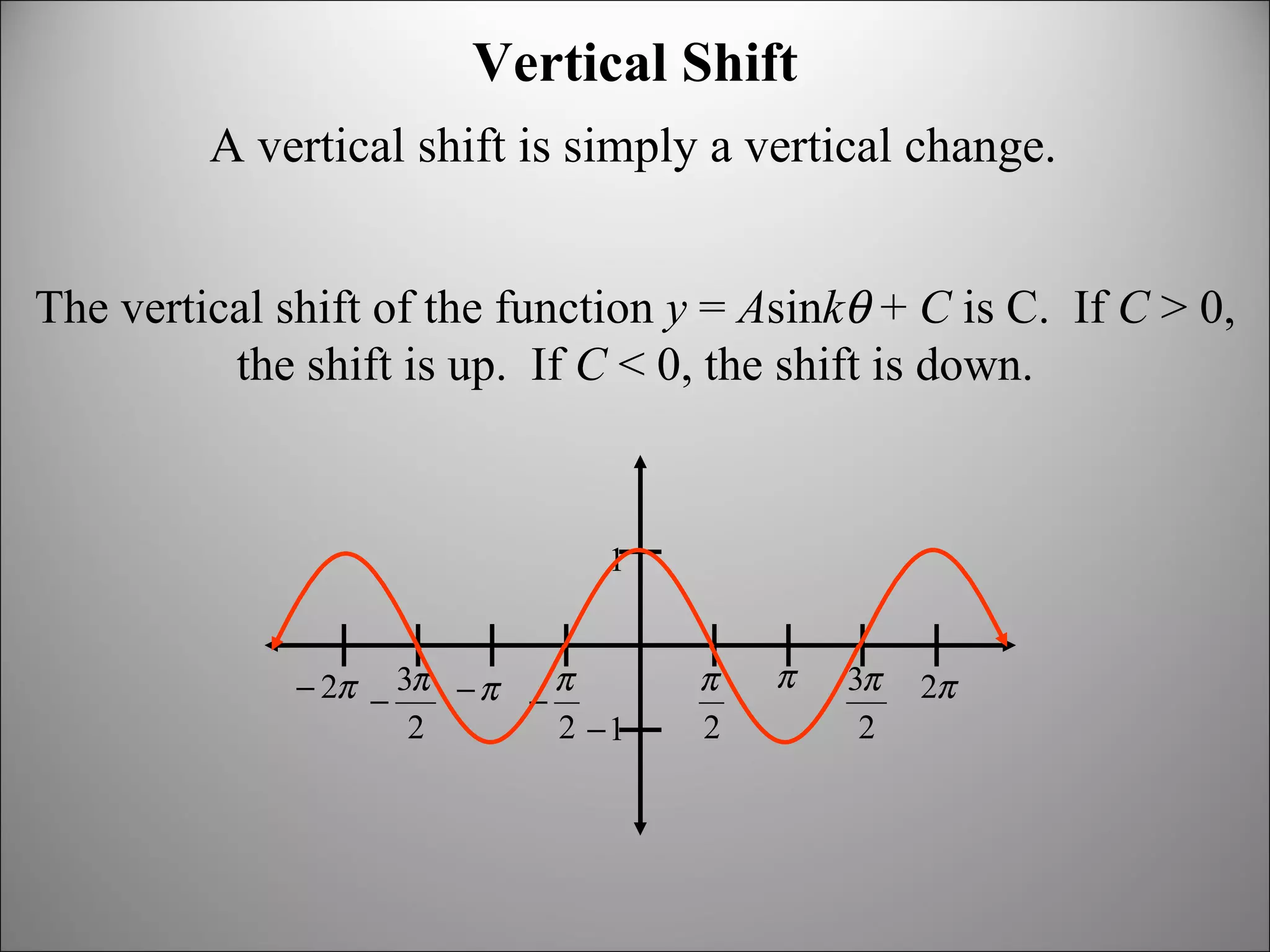
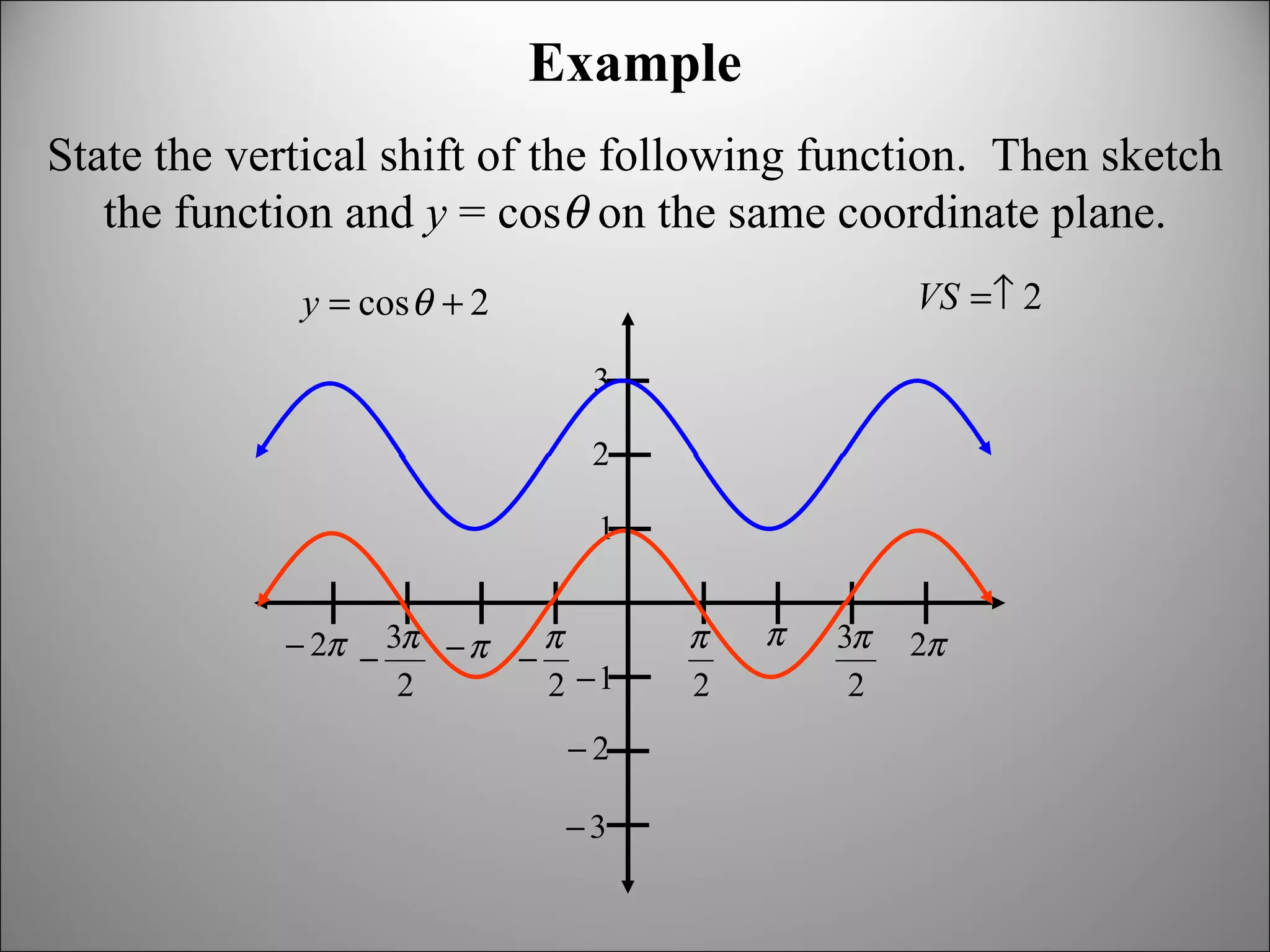
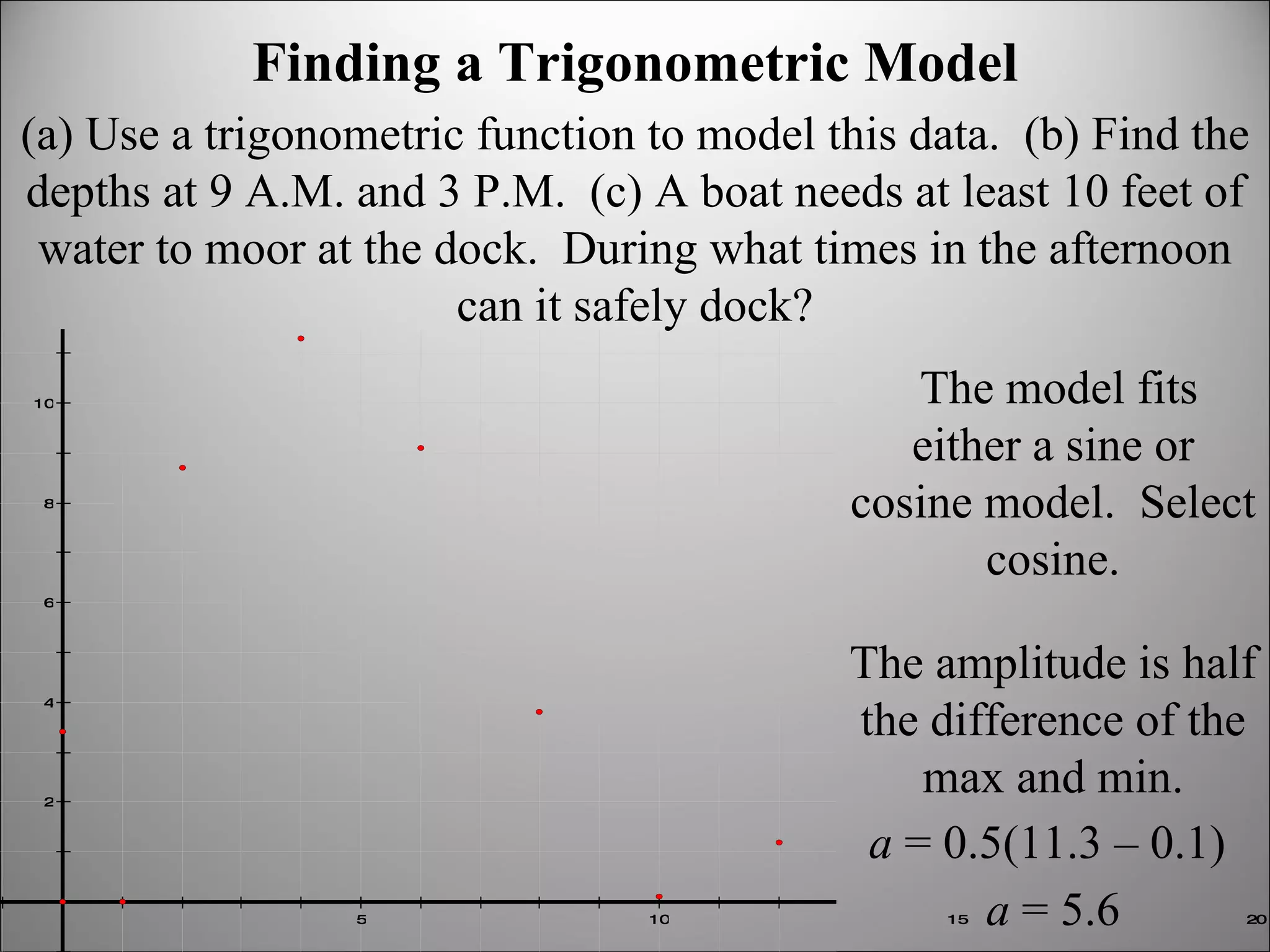
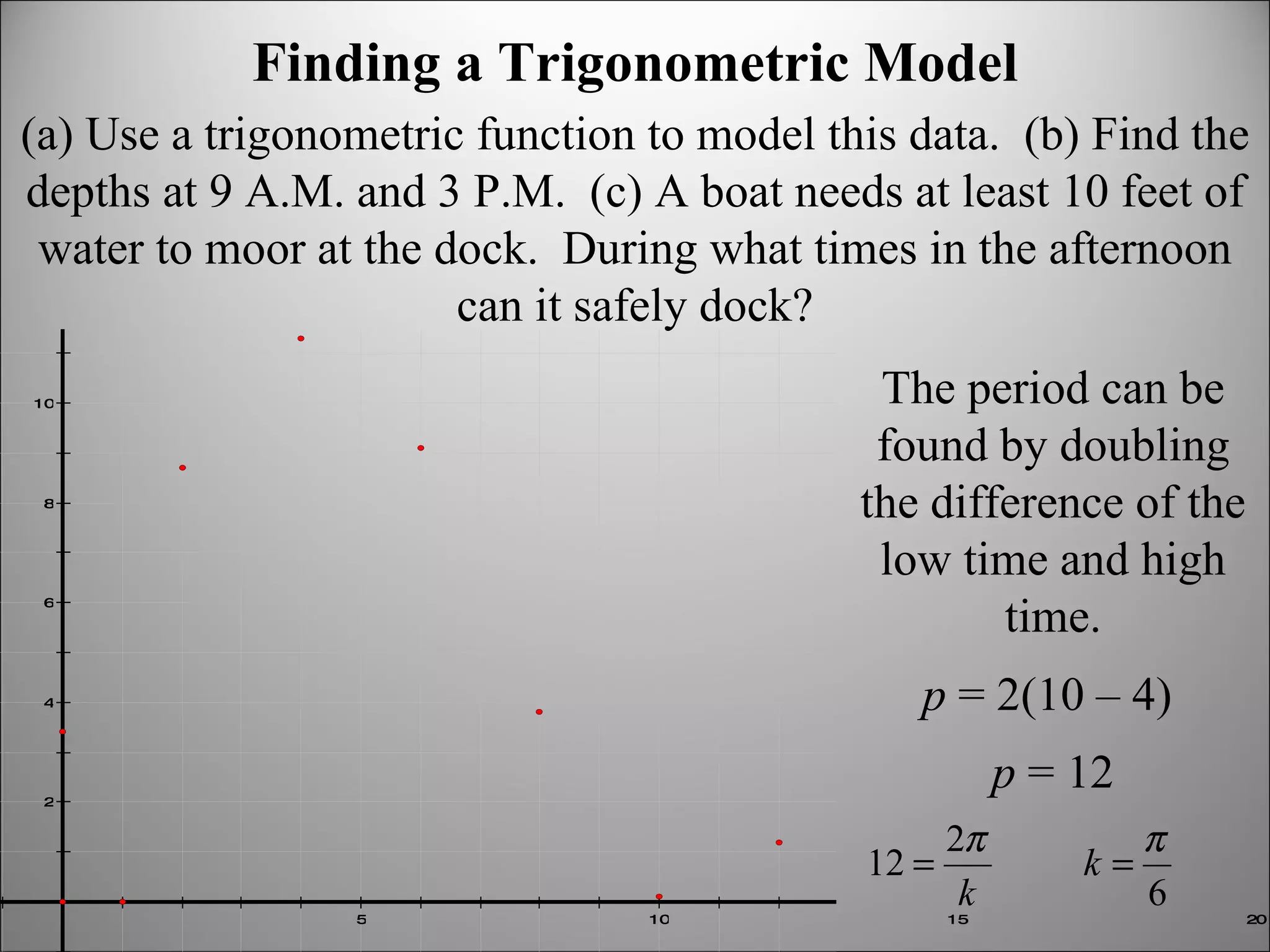
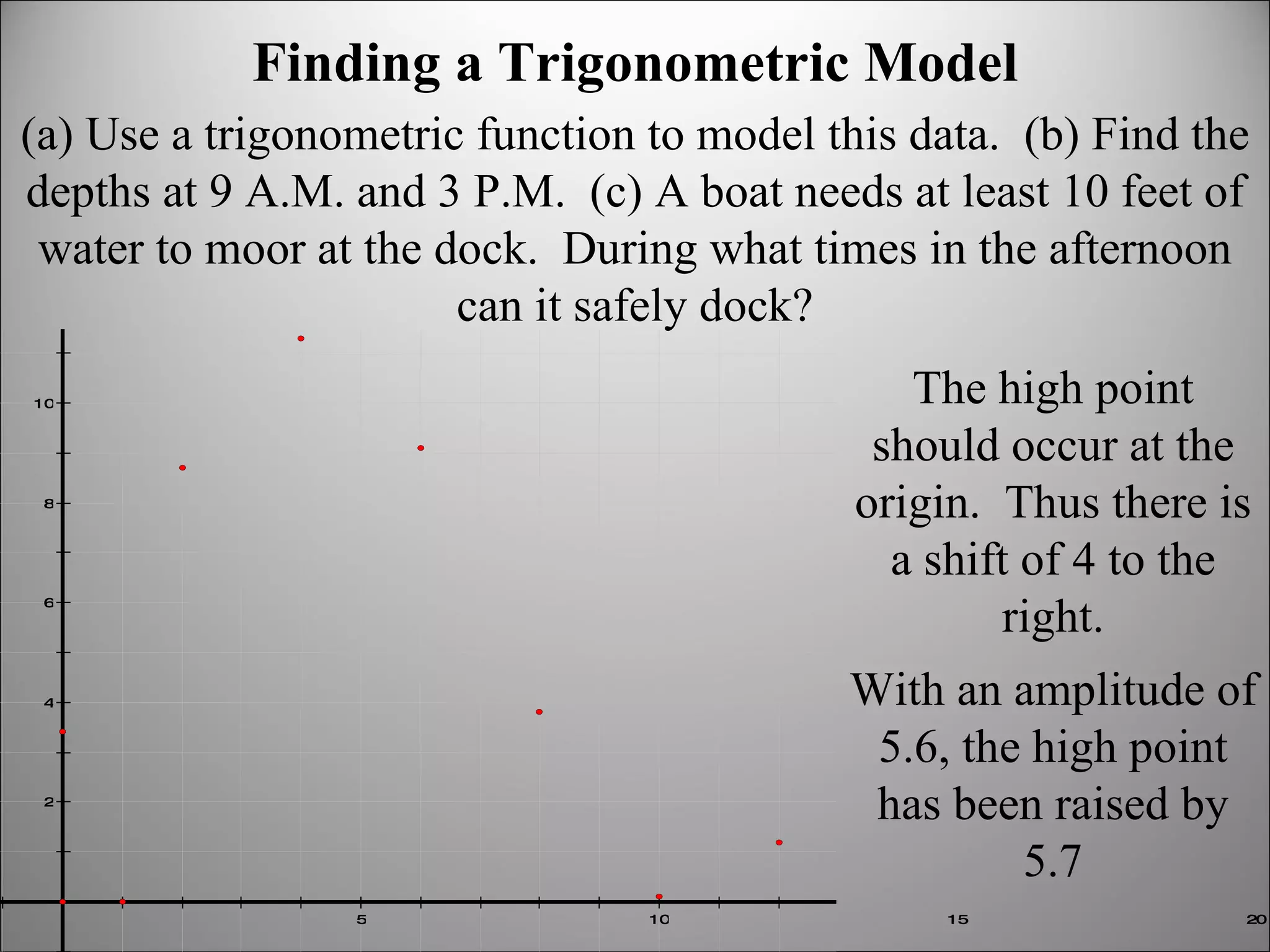
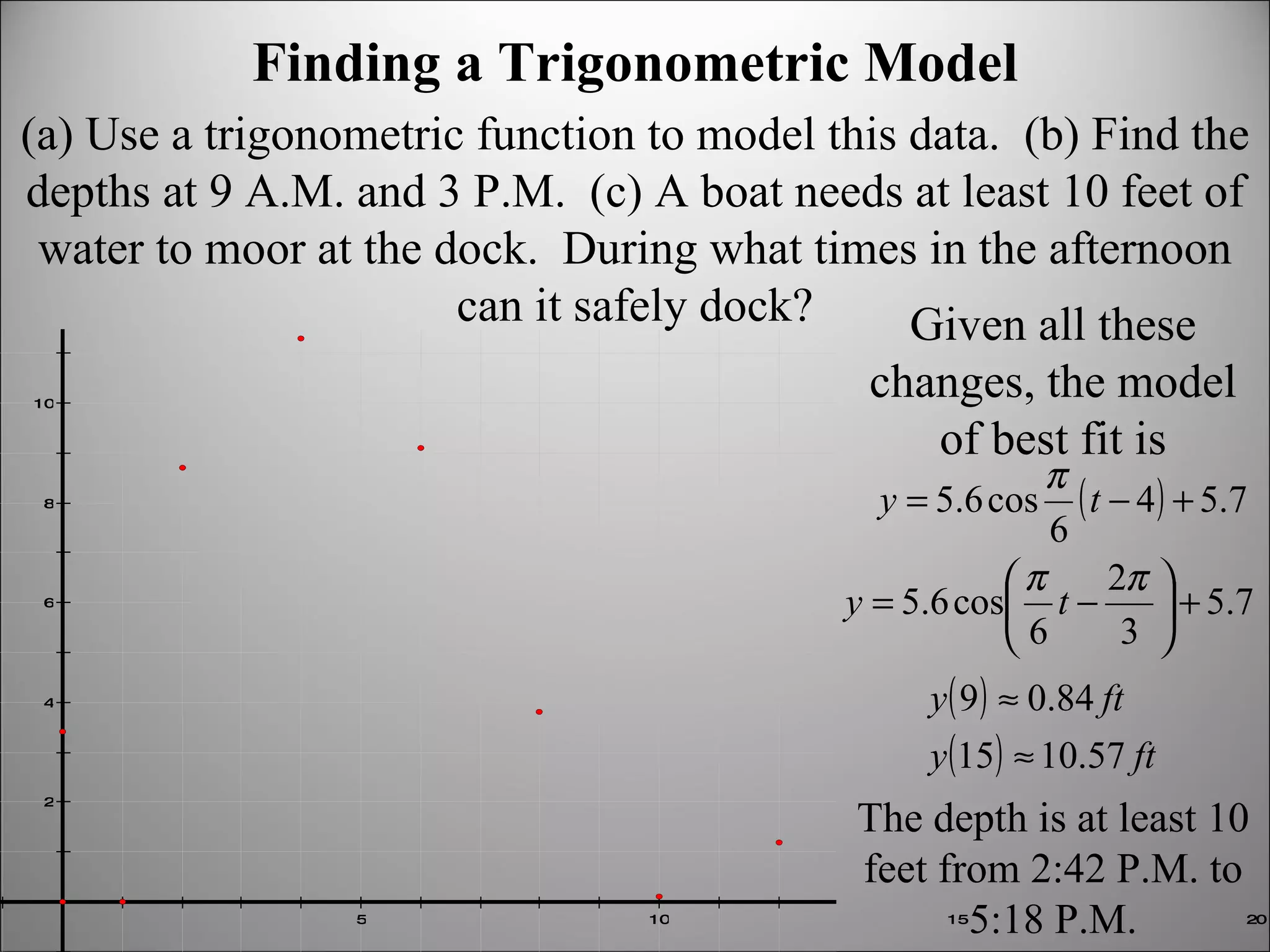
The document discusses trigonometric graphs and identities. It covers graphing sine and cosine functions including amplitude, period, translations involving phase shift and vertical shift. It also provides an example of using trigonometric functions to model real-life tidal data and finds the depth at specific times as well as time periods when a boat can safely dock.

1. Chapter 14 Trigonometric Graphs and Identities 14.1 Graphing Trig Functions

2. Graphs of Sine and Cosine Functions Objectives: to sketch the graphs of basic sine and cosine functions; to use amplitude and period to help sketch the graphs of sine and cosine functions; to sketch translations of the graphs of sine and cosine functions; to use sine and cosine functions to model real-life data.

3. Graph of Sine Domain: All Real Numbers Range: [-1, 1] Symmetry: Origin

4. Graph of Cosine Domain: All Real Numbers Range: [-1, 1] Symmetry: y -axis

5. Amplitude The amplitude of the functions y = A sin  and y = A cos  is the absolute value of A . The amplitude of a graph can be described as the absolute value of one-half the difference of the maximum and minimum function values.

6. Example State the amplitude of the function y = 3cos  . Graph both y = 3cos  and y = cos  on the same coordinate plane. A = 3

7. Period The period of a function is the distance required to complete one full cycle. The period of the functions y = sin k  and y = cos k  is given by:

8. Example State the period of the function y = cos4  . Graph both y = cos4  and y = cos  on the same coordinate plane.

9. Amplitudes and Periods

10. 14.2 Translations of Trig Graphs

11. The graph of y = A sin ( B x – C ) is obtained by horizontally shifting the graph of y = A sin B x so that the starting point of the cycle is shifted from x = 0 to x = C / B . The number C / B is called the phase shift . amplitude = | A | period = 2  / B . x y Amplitude: | A | Period: 2  / B The Graph of y = Asin(Bx - C) y = A sin Bx Starting point: x = C/B

12. Example Determine the amplitude, period, and phase shift of y = 2sin(3x-  ) Solution: Amplitude = |A| = 2 period = 2  /B = 2  /3 phase shift = C/B =  /3

13. Example cont. y = 2sin(3x-  )

14. Amplitude Period: 2 π /b Phase Shift: c/b Vertical Shift

15. Phase Shift A phase shift is simply a horizontal change. The phase shift of the function y = A cos k (  + C ) is C. If C > 0, the shift is to the left. If C < 0, the shift is to the right.

16. Example State the phase shift of the following function. Then sketch the function and y = cos  on the same coordinate plane.

17. Vertical Shift A vertical shift is simply a vertical change. The vertical shift of the function y = A sin k  + C is C. If C > 0, the shift is up. If C < 0, the shift is down.

18. Example State the vertical shift of the following function. Then sketch the function and y = cos  on the same coordinate plane.

19. Practice State the amplitude, period, phase shift, and vertical shift of the following function.

20. Finding a Trigonometric Model Throughout the day, the depth of water at the end of a dock in Bar Harbor, Maine, varies with the tides. The table below shows the depths (in feet) at various times during the morning. (a) Use a trigonometric function to model this data. (b) Find the depths at 9 A.M. and 3 P.M. (c) A boat needs at least 10 feet of water to moor at the dock. During what times in the afternoon can it safely dock? Begin by graphing the data. Let the time be the independent variable and the depth be the dependent variable. Time, t Depth, y Midnight 3.4 2 A.M. 8.7 4 A.M. 11.3 6 A.M. 9.1 8 A.M. 3.8 10 A.M. 0.1 Noon 1.2

21. Finding a Trigonometric Model (a) Use a trigonometric function to model this data. (b) Find the depths at 9 A.M. and 3 P.M. (c) A boat needs at least 10 feet of water to moor at the dock. During what times in the afternoon can it safely dock? The model fits either a sine or cosine model. Select cosine. The amplitude is half the difference of the max and min. a = 0.5(11.3 – 0.1) a = 5.6

22. Finding a Trigonometric Model (a) Use a trigonometric function to model this data. (b) Find the depths at 9 A.M. and 3 P.M. (c) A boat needs at least 10 feet of water to moor at the dock. During what times in the afternoon can it safely dock? The period can be found by doubling the difference of the low time and high time. p = 2(10 – 4) p = 12

23. Finding a Trigonometric Model (a) Use a trigonometric function to model this data. (b) Find the depths at 9 A.M. and 3 P.M. (c) A boat needs at least 10 feet of water to moor at the dock. During what times in the afternoon can it safely dock? The high point should occur at the origin. Thus there is a shift of 4 to the right. With an amplitude of 5.6, the high point has been raised by 5.7

24. Finding a Trigonometric Model (a) Use a trigonometric function to model this data. (b) Find the depths at 9 A.M. and 3 P.M. (c) A boat needs at least 10 feet of water to moor at the dock. During what times in the afternoon can it safely dock? Given all these changes, the model of best fit is The depth is at least 10 feet from 2:42 P.M. to 5:18 P.M.

25. Homework 14.1 pg 767 #’s 15, 18, 21, 24, 27, 30, 33 14.2 pg 774 #’s 19-24 all