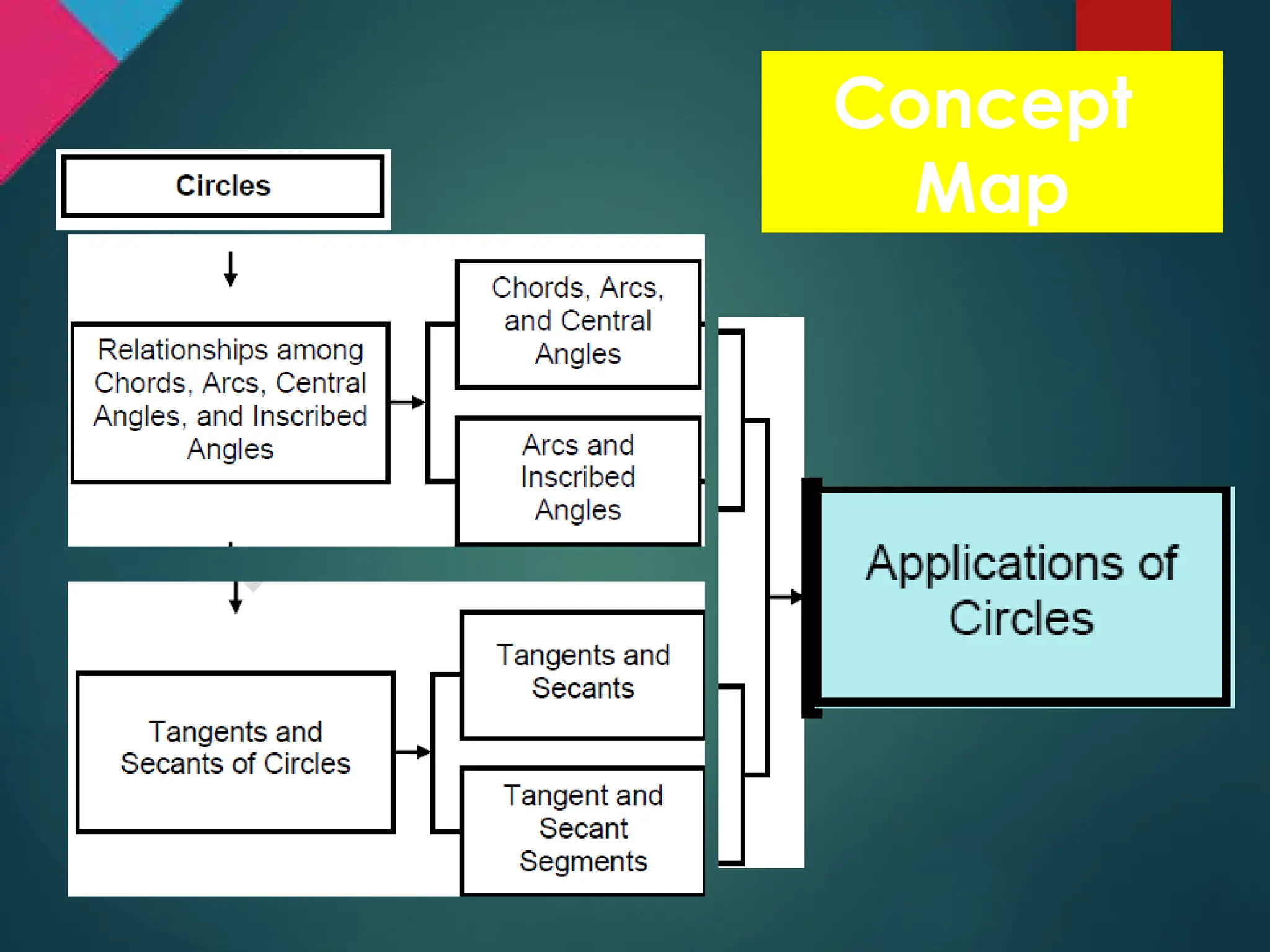
The document outlines a group activity focused on solving word problems related to circles, incorporating directions, review questions, and problem-solving strategies. It includes various problems involving circumference, angles formed by circles, and geometric relationships, along with examples and corresponding answers. The material emphasizes collaborative learning and applying Polya's four-step process for effective problem-solving.

1. SOLVING
WORD
PROBLEMS
CIRCLES

2. Concept
Map

3. OBJECTIVE:
Solve
problems on
circles.
(M10GE-Iif-2)
?

4. REVIEW:What’s the Word? That’s the Word!
Directions:
Work by group. Solve the
unknown. Find the letter that
corresponds to your answer.(3
minutes)
Scor
e-
Tab
Grou
p
Yell…

5. REVIEW:What’s the Word? That’s the Word!
Directions:
Work by group. Solve the unknown. Find the letter that
corresponds to your answer. (3 minutes)
1.
C=
?
2.
3. 4.
6
45
Length of
A
B
No. 4 3 1 2 4 3
Letter
Letter Possible
Answers
A 52.5
E 47
F 45
G 40
L 37.8
N 35.2
O 31.4
P 8.1
R 4.7
paper
timer

6. REVIEW: What’s the Word? That’s the Word
Directions:
Work by group. Solve the unknown. Find the letter that
corresponds to your answer.
1.
C=
?
C= 10
(3.14)
C=
31.4
Letter O
No. 4 3 1 2 4 3
Letter
Letter Possible
Answers
A 52.5
E 47
F 45
G 40
L 37.8
N 35.2
O 31.4
P 8.1
R 4.7
O
Circumference - distance around the
circle

7. REVIEW:What’s the Word? That’s the Word!
Directions:
Work by group. Solve the unknown. Find the letter that
corresponds to your answer.
l= 4.7
Letter: R
No. 4 3 1 2 4 3
Letter O
Letter Possible
Answers
A 52.5
E 47
F 45
G 40
L 37.8
N 35.2
O 31.4
P 8.1
R 4.7
R

8. REVIEW:What’s the Word? That’s the Word!
Directions:
Work by group. Solve the unknown. Find the letter that
corresponds to your answer.
3.
The measure of an angle formed by secants
intersecting inside the circle equals one-half the sum
of the measures of the arc intercepted by the angle
and its vertical angle pair.
= ( + )
= ( 45 + 49)
= ( 94)
=47
Letter: E
No. 4 3 1 2 4 3
Letter O R
Letter Possible
Answers
A 52.5
E 47
F 45
G 40
L 37.8
N 35.2
O 31.4
P 8.1
R 4.7
E
E
siic

9. REVIEW:What’s the Word? That’s the Word!
Directions:
Work by group. Solve the unknown. Find the letter that
corresponds to your answer.
4.
No. 4 3 1 2 4 3
Letter E O R E
Letter Possible
Answers
A 52.5
E 47
F 45
G 40
L 37.8
N 35.2
O 31.4
P 8.1
R 4.7
The measure of an angle formed by two
tangents from a common external point is
equal to one-half the difference of the major
arc minus the minor arc.
= ( - )
= (220 - 140)
= (80)
=40
Letter: G G G
2Tfc
exp

10. No. 4 3 1 2 4 3
Letter
REVIEW:What’s the Word? That’s the Word!
The word is
GEORGE.
G E O R G E

11. Polya’s 4-step Process for Problem
Solving
Step 1: Understand the problem.
.
Step 2: Devise a plan (translate).
Step 3: Carry out the plan (solve).
Step 4: Look back (check)
LS

12. ACTIVITY:We Can Do This! Part 1 (8
members)
Scoring:
1 – Given & Unknown
1 – Solution
1 – Answer
Total: 3 points
Groups 1, 2 & 3 Visual
Groups 4, 5 & 6
Kinesthetic
Presentations:
2 presentations in every problem and explain
the answer
1 Visual Group
1 Kinesthetic Group
Dw
L

13. ACTIVITY:
Lala cycled to Banisil National
High School. Find the distance
travelled by Lala if her bicycle
wheels rotated 840 times and the
radius is 0.25 m.
Problem 1 (5 minutes)
We Can Do This! Part 1 (8
members)
Yell
Pick 2
P
Answer: 1,318.8
m
Perf
Score

14. Perf
ACTIVITY:
Lala cycled to
Busok National High
School. Find the distance
travelled by Lala if her
bicycle wheels rotated
840 times and the radius is
0.25 m.
Problem 1 (5 minutes)
We Can Do This! Part 1 (8
members)
Y &
Game
s
2....
r
P
Sc
Answer: 1,318.8
m
Given:
r = 0.25 m
rev = 840
Unknown:
C = ?
C = 2 r
C = 2(3.14)(0.25m)
C = 1.57 m (for 1 rev)

15. ACTIVITY:
Pedro watched a bakukang
crawl through an arc of 12° along
the rim of his watermelon, which
was cut in half. If the radius of the
watermelon was 9 inches, how far
did the bug crawl?
Problem 2 (5 minutes)
We Can Do This! Part 2 (4
members)
Answer: 1.884 in
Yell
Pick 2
P
Perf
Score

16. Perf
ACTIVITY:
Pedro watched
a bakukang crawl
through an arc of 12°
along the rim of his
watermelon, which
was cut in half. If the
radius of the
watermelon was 9
inches, how far did
the bug crawl?
Problem 2 (5 minutes)
We Can Do This! Part 2 (4
members)
Y
2....
r
P
Sc
Answer: 1.884 in
𝐴
360
=
𝑙
2 𝜋 𝑟
12
360
=
𝑙
2 𝜋(9)
1
30
=
𝑙
18 𝜋
Given:
r = 9 in
degree = 12
Unknown:
= ?

17. ACTIVITY:
Two straight pipes intersect the
school circular garden and
intercept non-adjacent arcs that
measure 38° and 40°. What is the
supplementary angle formed by two
intersecting pipes?
Problem 3 (5 minutes)
We Can Do This! Part 3 (2
members)
Answer: 141°
Yell
Pick 2
P
Perf
Score

18. Perf
ACTIVITY:
Two straight
pipes intersect the
school circular
garden and
intercept non-
adjacent arcs that
measure 38° and 40°.
What is the
supplementary angle
formed by two
intersecting pipes?
Problem 3 (5 minutes)
We Can Do This! Part 3 (2
members)
Y
2....
r
P
Sc
Answer: 141°
x = (40 + 38 )
40
38
Given: Non-adjacent arcs that measure 38° and
40°
Unknown: x = angle formed by secants intersecting
inside the circle
y = supplementary angle formed by two
intersecting pipes
x
y
x = (78)
x = (78)
x = y =
y =
Note: The measure of a central angle is
equal to the measure of its intercepted

19. ACTIVITY:
In Rizal Plaza, the maintenance
person stands outside from a circular
monument. If you assume her lines of
sight form tangents to the monument
and make an angle of 40°, what is the
measure of the arc of the monument
that her lines of sight intersect?
Problem 4 (5 minutes)
We Can Do This! Part 4
( Individual)
Answer: 140
° Score
Yell
Pick 2
P
Perf
Score

20. Perf
ACTIVITY:
In Bonifacio Plaza,
the maintenance person
stands outside from a
circular monument. If you
assume her lines of sight
form tangents to the
monument and make an
angle of 40°, what is the
measure of the arc of the
monument that her lines of
sight intersect?
Problem 4 (5 minutes)
We Can Do This! Part 4
( Individual)
Y
2....
r
P
Sc
Answer: 140
°
Score
4
40 = (major arc - major
arc)
x
40 = (360 )
360 - x
40 = (360)
40 = 180 - x
x = 140
Given: Angle formed by two tangents from a
common external point = 4
Unknown: x = measure of the arc of the
monument that her lines of sight
intersect

21. QUIZ
BOWL
Loss

22. Problem 1 (2 points for 1 minute)
Answer: 39.81
m
Eugenio ran around a
circular field 3 times. If he ran
a total distance of 750 m,
radius of the field?
# 3
Scor
e

23. Problem 1 (2 points for 1 minute)
Answer: 39.81
m
Eugenio
ran around a
circular field 3
times. If he
ran a total
distance of
750 m, radius
of the field?
# 3
Scor
e
3𝐶=750𝑚
𝐶=250𝑚
250
250
2 𝜋
=𝑟

24. Problem 2 (2 points for 1 minute)
Answer: 18.84
m
Eulah has a circular
garden that she separates
into three equal parts. If the
radius of the garden is 9 m,
what is the length of the arc
of each part?
# 7
Scor
e

25. Problem 2 (2 points for 1 minute)
Answer: 18.84
m
Eulah has a
circular garden
that she
separates into
three equal parts.
If the radius of the
garden is 9 m,
what is the length
of the arc of
each part?
# 7
Scor
e
1
𝐴
360
=
𝑙
2 𝜋 𝑟
120
360
=
𝑙
2 𝜋(9)
1
3
=
𝑙
18 𝜋

26. Problem 3 (3 points for 30 seconds)
Answer: 120 °
Jessa has a necklace
with a circular pendant
hanging from a chain around
her neck. The chain is tangent
to the pendant. If the chain is
extended as shown in the
diagram on the right, it forms
an angle of 60° below the
pendant. What is the measure
of the arc at the bottom of the
pendant?
# 1
Scor
e

27. Problem 3 (3 points for 30 seconds)
Answer: 120 °
Jessa has a
necklace with a
circular pendant
hanging from a chain
around her neck. The
chain is tangent to the
pendant. If the chain
is extended as shown
in the diagram on the
right, it forms an angle
of 60° below the
pendant. What is the
measure of the arc at
the bottom of the
pendant?
# 1
Scor
e
60
60 = (major arc - major
arc)
x
60 = (360 )
60 = (360)
60 = 180 - x
x = 120

28. Problem 4 (3 points for 30 seconds)
Answer: 78.5
2
A piece of plywood that is
100 cm2
is cut into a circular
shape. What is the maximum
area of a circle that can be
contained in that plywood?
# 5
Scor
e

29. Problem 4 (3 points for 30 seconds)
Answer: 78.5
2
A piece of
plywood that is
100 cm2
is cut
into a circular
shape. What is
the maximum
area of a circle
that can be
contained in that
plywood?
# 5
Scor
e
A =
A =
10 cm
A = (3.14)( )

30. Problem 5 (5 points for 1 minute)
Answer: 91.65
The figure shows a sketch a circular
children’s park and different pathways
from the main road. If the distance from
the main road to Gate 2 is 70 m and the
length of the pathway from Gate 2 to the
Exit is 50 m, about how far from the main
road is Gate 1?
# 1
Scor
e

31. Problem 5 (5 points for 1 minute)
Answer: b=91.65
The figure
shows a sketch a
circular children’s
park and different
pathways from the
main road. If the
distance from the
main road to Gate
2 is 70 m and the
length of the
pathway from Gate
2 to the Exit is 50 m,
about how far from
the main road is
# 1
Scor
e
70 m
50 m
?
b = 95
m
?
a = 25
m
c2
=
(95 m)2
= (25m)
9,025 m2
= 625m
= 9,025 m2
- 625m
= 8,400 m2

32. Content, graphics and text
belong to the rightful
owner.
No copyright intended