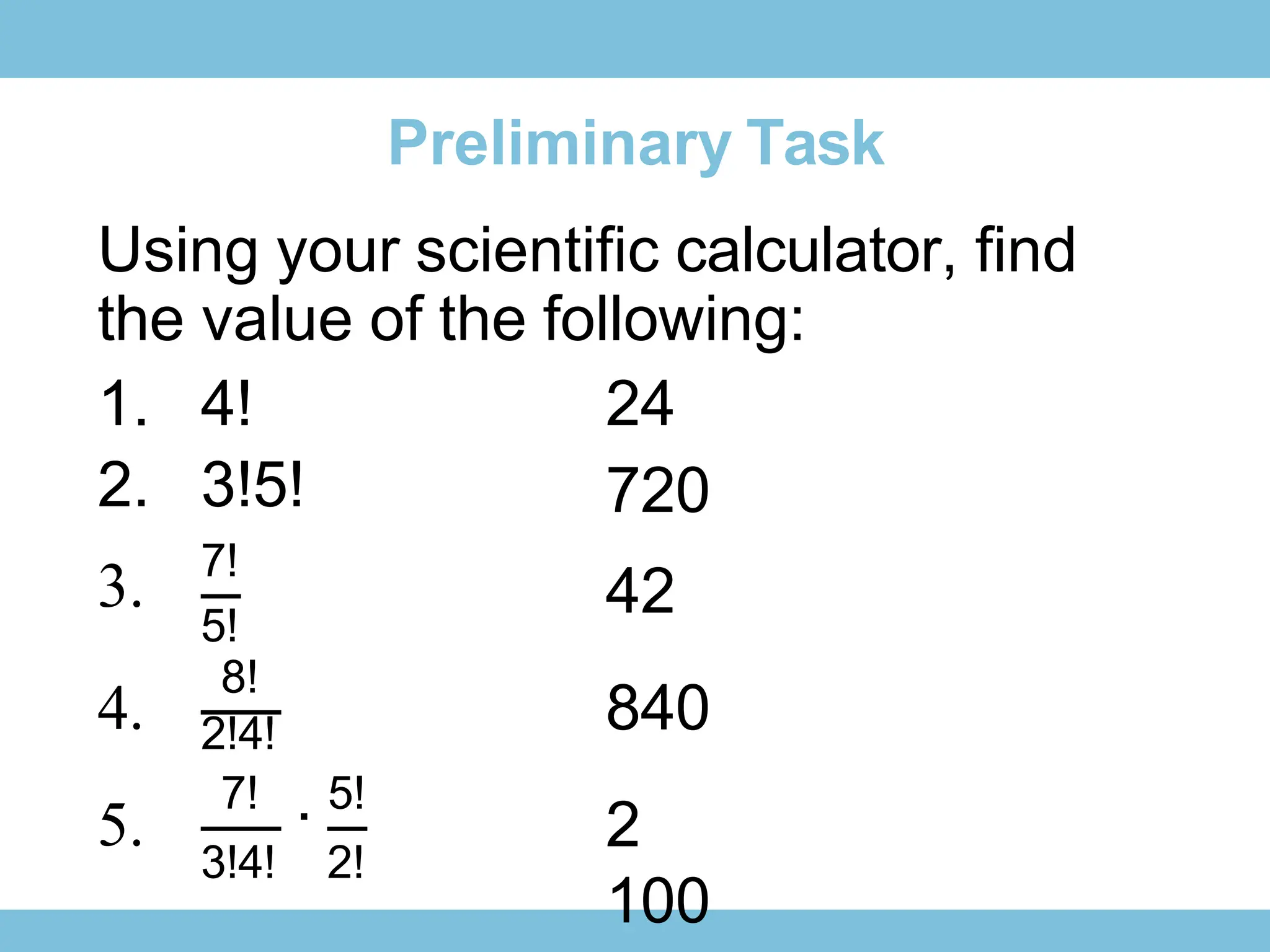
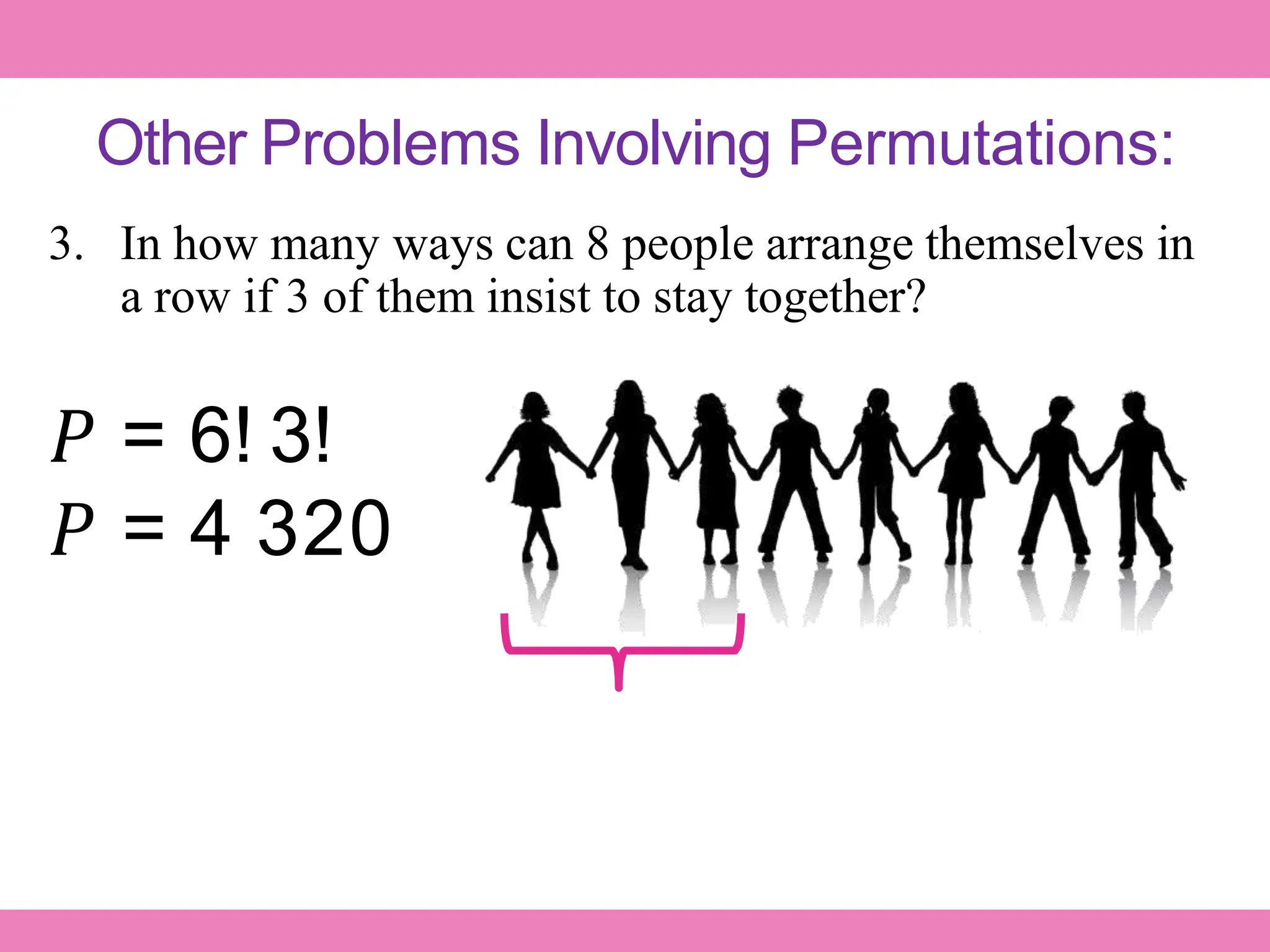
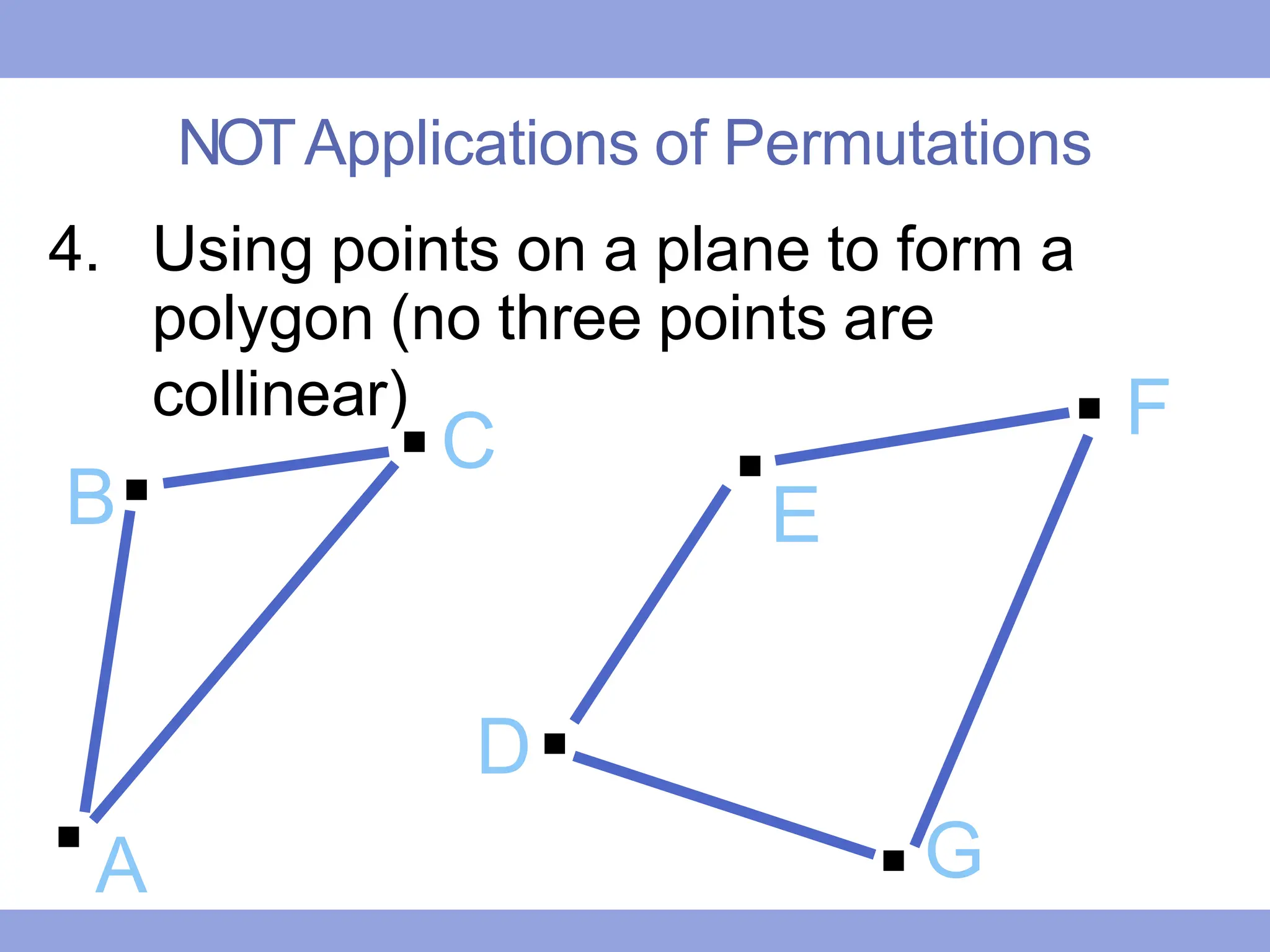
The document discusses permutations, outlining their definitions, types, and calculations using factorials. It provides examples of how to calculate permutations for different scenarios, including arrangements of objects and distinguishable permutations with identical items. Additionally, it explores applications of permutations in various contexts, such as organizing books, seating arrangements, and selecting contest winners.

2. Note
Please prepare your
scientific calculator as it will
be used in our discussion.

3. PERMUTATION
An arrangement of objects in a definite
order or the ordered arrangement of
distinguishable objects without
allowing repetitions among the objects.

4. Preliminary Task
Using your scientific calculator, find
the value of the following:
1. 4!
2. 3!5!
3. 7!
24
720
42
840
2
100
5!
8!
4.
5.
2!4!
7!
∙ 5!
3!4! 2!

5. What is meant by 𝑛! (𝑛 factorial)
𝑛! = 𝑛(𝑛 − 1)(𝑛 − 2)(𝑛 − 3) …
Example:
4! = 4 3 2
1
4! = 24

6. Types of Permutation
1. Permutation of 𝑛 objects
2. Distinguishable Permutation
3. Permutation of 𝑛 objects taken 𝑟 at a
time
4. Circular Permutation

7. Permutation of 𝑛 objects
𝒏𝑷
𝒏
= 𝒏!
(The permutation of 𝑛 objects
is equal to 𝑛 factorial)

8. How many arrangements are there?
1. Arranging different 3 portraits on a
wall
𝟑! = 𝟔

9. How many arrangements are there?
2.Arranging 4 persons in a row for a picture
taking
𝟒! = 𝟐𝟒
3.Arranging 5 different figurines in a shelf
𝟓! = 𝟏𝟐𝟎
4.Arranging 6 different potted plants in a row
𝟔! = 𝟕𝟐𝟎
5.Arranging the digits of the number 123456789
𝟗! = 𝟑𝟔𝟐 𝟖𝟖𝟎
6.Arranging the letters of the word
CHAIRWOMEN
𝟏𝟎! = 𝟑 𝟔𝟐𝟖 𝟖𝟎𝟎

10. Distinguishable Permutation
𝑷 =
𝒏!
𝒑!𝒒!𝒓!
There are repeated (or identical) objects
in the set.

11. How many arrangements are there?
1. Arranging the digits in the number 09778210229
𝑃 =
11!
2! 2! 2! 3!
= 831
600
2. Drawing one by one and arranging in a row 4
identical blue, 5 identical yellow, and 3
identical red balls in a bag
𝑃 =
12!
3! 4! 5!
= 27
720

12. How many arrangements are there?
3. Arranging the letters in the word
LOLLIPOP 𝑃 =
8!
3! 2! 2!
= 1680
4. Arranging these canned
goods
𝑃 =
10!
3! 4!
= 25
200

13. Permutation of 𝑛 objects taken 𝑟
𝒏𝑷𝒓 =
𝒏!
𝒏−𝒓 !
Permutation of 𝑛 taken 𝑟 at a time
where
𝑛 ≥ 𝑟

14. How many arrangements are there?
1. Choosing 3 posters to hang on a wall from 5
posters you are keeping
𝒏 𝒓
𝑷 =
𝒏!
𝒏−𝒓 !
𝟓!
𝟓
𝟑
𝑷 =
𝟓−𝟑 !
𝟓!
𝟓𝑷𝟑 =
𝟐!
𝟓𝑷𝟑 = 𝟔
𝟎
Notation: 5P3 / P(5,3) Calculator: 5 shift 𝒏𝑷𝒓 3

15. How many arrangements are there?
2. Taking two-letter word, without repetition of letters,
from the letters of the word COVID
Examples: CO, OC, VD, …
𝒏 𝒓
𝑷 =
𝒏!
𝒏−𝒓 !
𝟓!
𝟓
𝟐
𝑷 =
𝟓−𝟐 !
𝟓
𝟐
𝑷 = 𝟓!
𝟑!
𝟓𝑷𝟐 = 𝟐
𝟎
Notation: 5P2 / P(5,2) Calculator: 5 shift 𝒏𝑷𝒓 2
=

16. How many arrangements are there?
3. Taking four-digit numbers, without repetition of
digits, from the number 345678
Examples: 3456, 6534, 6745, …
𝒏 𝒓
𝑷 =
𝒏!
𝒏−𝒓 !
𝟔!
𝟔
𝟒
𝑷 =
𝟔−𝟒 !
𝟔
𝟒
𝑷 = 𝟔!
𝟐!
𝟔𝑷𝟒 = 𝟑𝟔𝟎
Notation: 6P4 / P(6,4) Calculator: 6 shift 𝒏𝑷𝒓 4
=

17. How many arrangements are there?
4. Pirena, Amihan, Alena, and Danaya competing for
1st, 2nd, and 3rd places in spoken poetry
Example: Danaya–1st, Alena–2nd, Amihan–3rd
𝒏 𝒓
𝑷 =
𝒏!
𝒏−𝒓 !
𝟒!
𝟒
𝟑
𝑷 =
𝟒−𝟑 !
𝟒!
𝟒𝑷𝟑 =
𝟏!
𝟒𝑷𝟑 = 𝟐
𝟒
Notation: 4P3 / P(4,3) Calculator: 4 shift 𝒏𝑷𝒓 3
=

18. How many arrangements are there?
5. Electing Chairperson, Vice Chairperson,
Secretary, Treasurer, Auditor, PRO, and Peace
Officer from a group of 20 people
𝒏 𝒓
𝑷 =
𝒏!
𝒏−𝒓 !
𝟐𝟎!
𝟐𝟎
𝟕
𝑷 =
𝟐𝟎−𝟕
!𝟐𝟎!
𝟐𝟎𝑷𝟕 =
𝟏𝟑
!
𝟐𝟎𝑷𝟕 = 𝟑𝟗𝟎 𝟕𝟎𝟎 𝟖𝟎𝟎
Notation: 20P7 / P(20,7) Calculator: 20 shift 𝒏𝑷𝒓 7
=

19. Circular Permutation
𝑷 = (𝒏 − 𝟏)!

20. How many arrangements are there?
How many ways can 5 people sit around a
circular table?
𝑃 = (5 − 1)!
𝑃 = 4!
𝑃 = 24

22. Other Problems Involving Permutations:
1. There are 3 different History books, 4 different
English books, and 8 different Science books. In
how many ways can the books be arranged if
books of the same subjects must be placed
together?
𝑃 = 3! 4! 8! 3!
𝑃 = 34 836
480

23. Other Problems Involving Permutations:
2. Three couples want to have their pictures taken. In how
many ways can they arrange themselves in a row if
couples must stay together?
𝑃 = 3! 2!
𝑃 = 12

24. Other Problems Involving Permutations:
3. In how many ways can 8 people arrange themselves in
a row if 3 of them insist to stay together?
𝑃 = 6! 3!
𝑃 = 4 320

25. Other Problems Involving Permutations:
4. In how many ways can the letters of the word
ALGORITHM be arranged if the vowel letters are
placed together?
Example: AOILGRTHM
𝑃 = 7! 3!
𝑃 = 30
240

26. Other Problems Involving Permutations:
5. In how many ways can the letters of the word
TIKTOKERIST be arranged if the consonant letters
are placed together?
Example: TKTKRSTIOEI
𝑃 = ∙
5! 7!
2! 2! 3!
𝑃 = 25
200

27. Other Problems Involving Permutations:
6. In how many ways can 7 people be seated around a
circular table if 3 of them insist on sitting beside each
other?
𝑃 = 5 − 1 ! ∙ 3!
𝑃 = 144

29. Applications of Permutations
1.Using passwords
022988, 228890
2.Using PIN of ATM cards
1357, 3715
3.Winning in a contest
Erika – 1st, Carrie – 2nd, Agatha –
3rd Agatha – 1st, Erika – 2nd, Carrie
– 3rd

30. Applications of Permutations
4.Electing officers in an organization
Gerald – President, Julia – VP, Bea –
Secretary Bea – President, Gerald – VP,
Julia – Secretary
5.Assigning of telephone/mobile
numbers 09778210229,
09228210779
6.Assigning plate numbers of vehicles
ABY 8512, BAY 1258

32. NOTApplications of Permutations
1.Selecting numbers in a lottery
6-12-25-32-34-41, 34-25-41-6-32-12
2.Selecting fruits for salad
apple, pineapple, grapes, papaya,
pears papaya, pears, apple,
pineapple, grapes
3.Choosing members of a committee
Marissa, Ellice, Gabriel,
Lucinda Lucinda, Gabriel,

33. NOTApplications of Permutations
4. Using points on a plane to form a
polygon (no three points are
collinear) .
.
. . .
B
A
C
D.
E
.G
F