Downloaded 686 times
SR
Uploaded bySrinivasan R
14,032 views
Machine learning Lecture 3
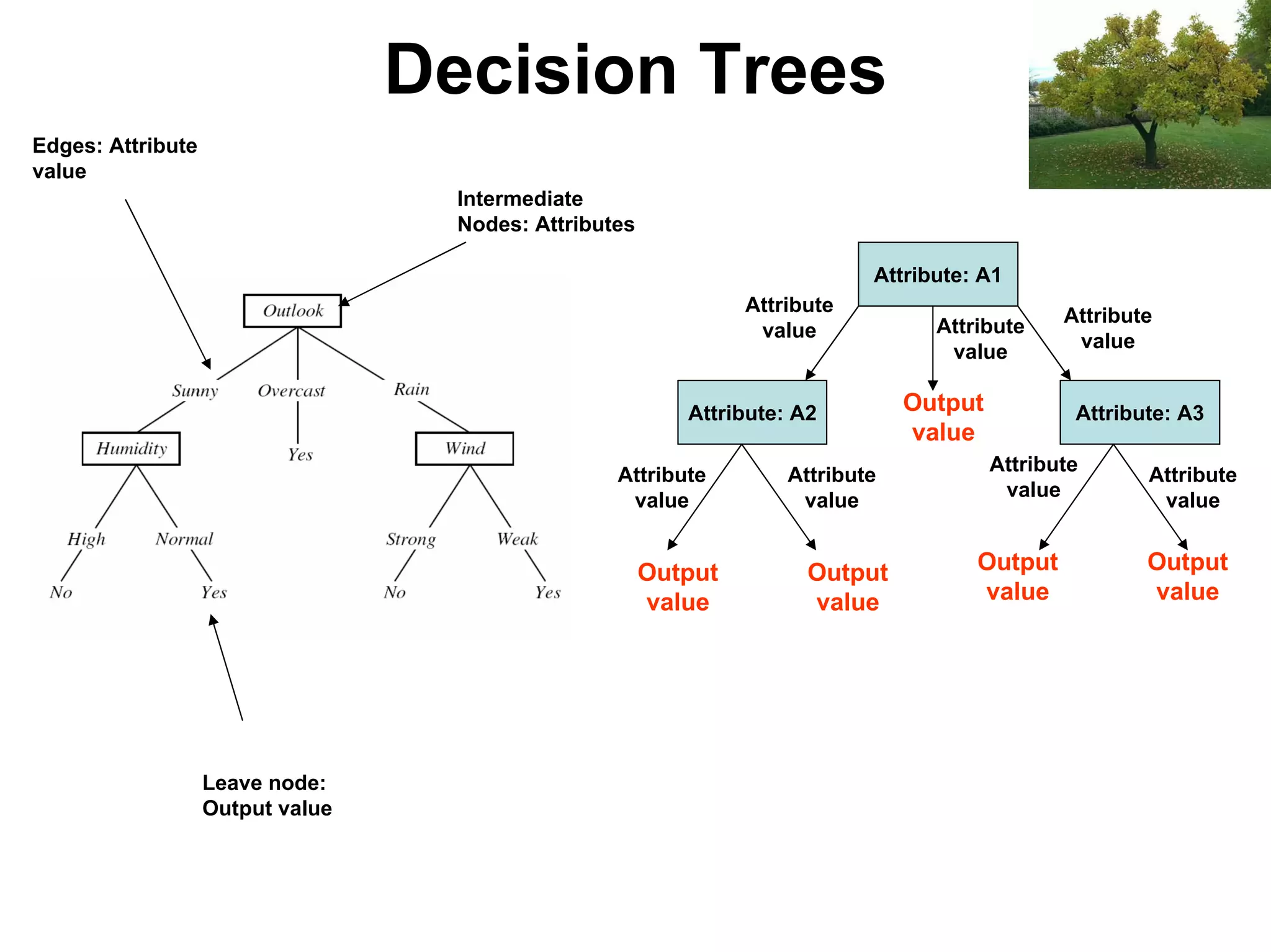
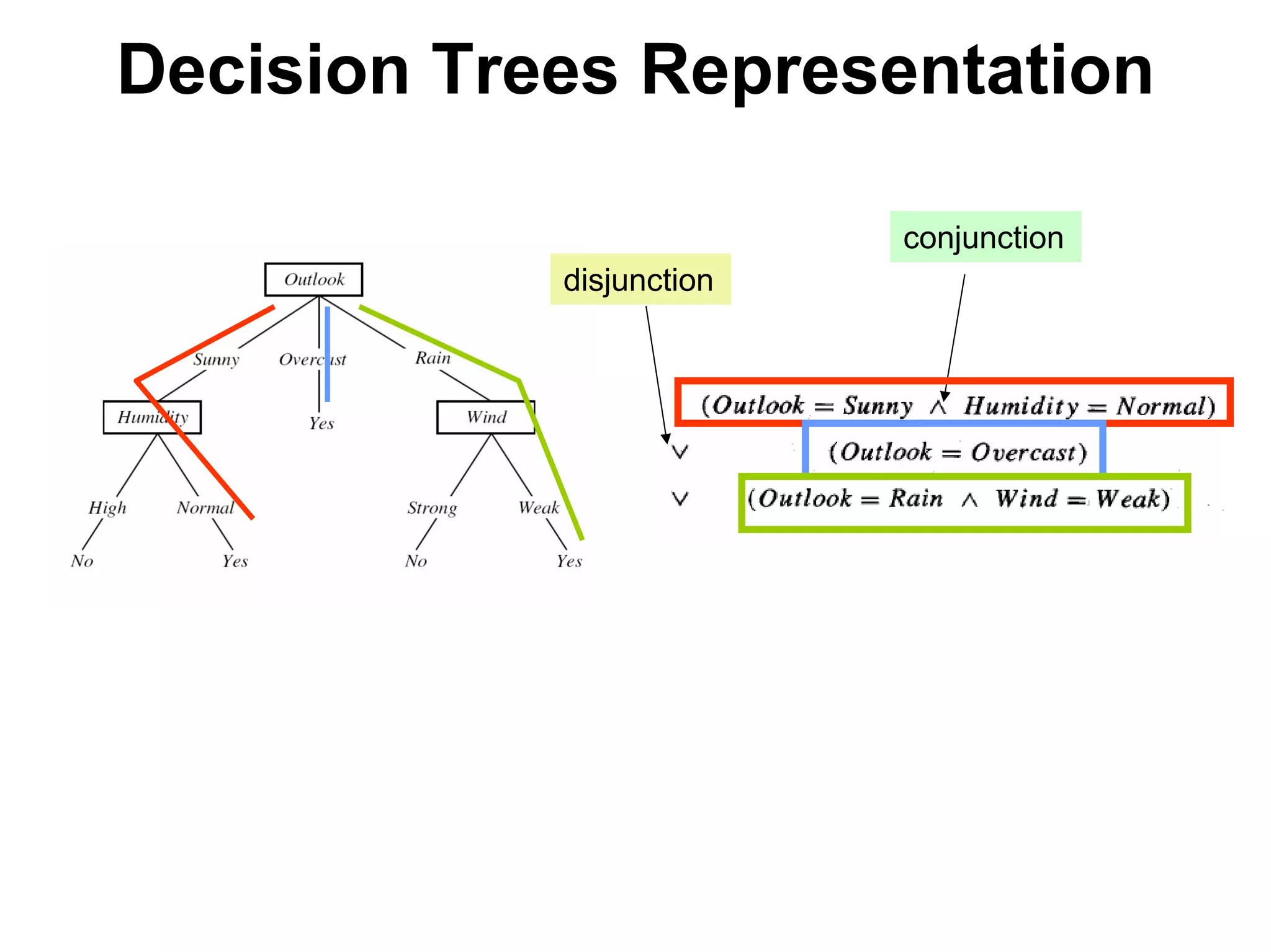
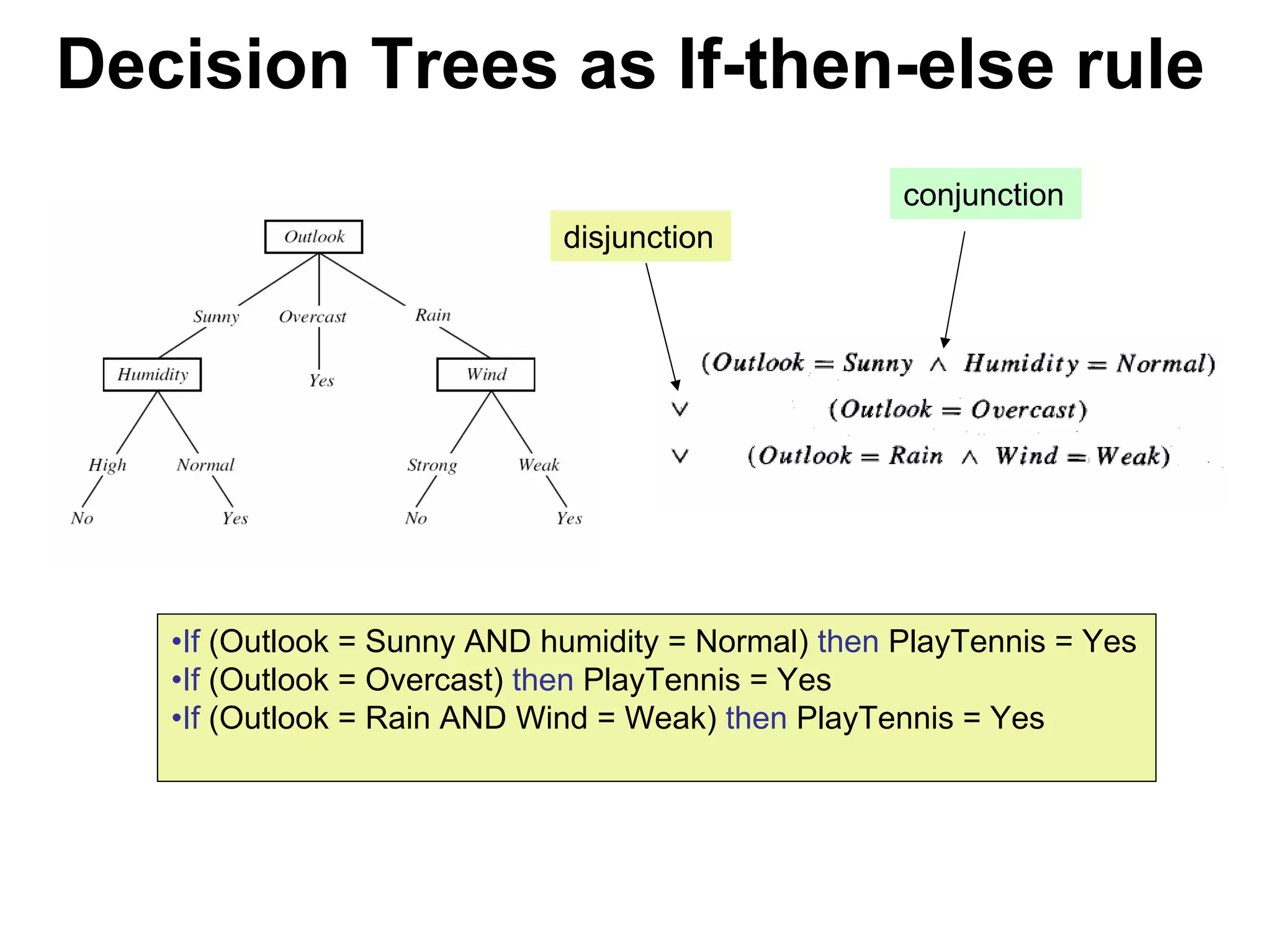
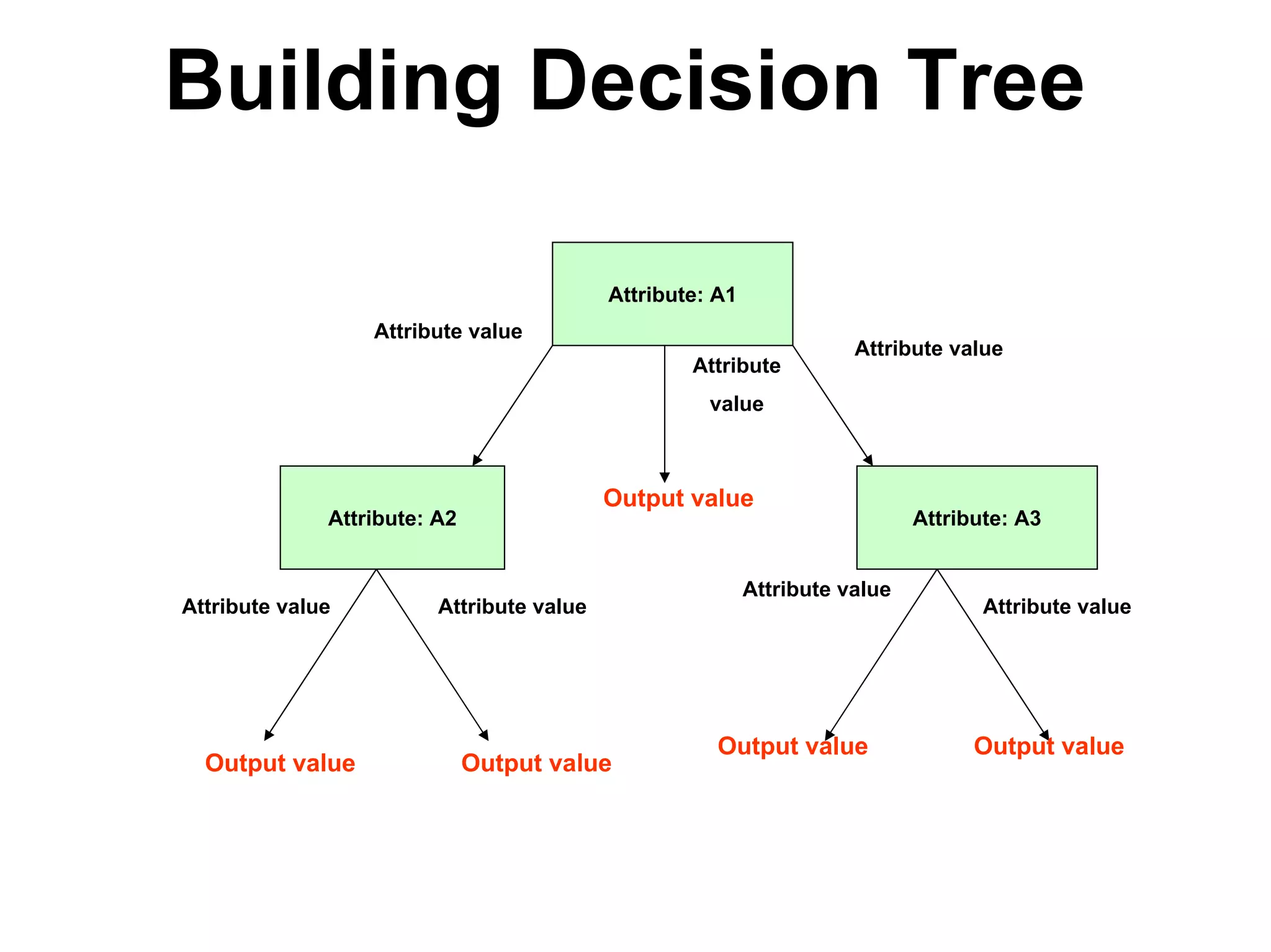
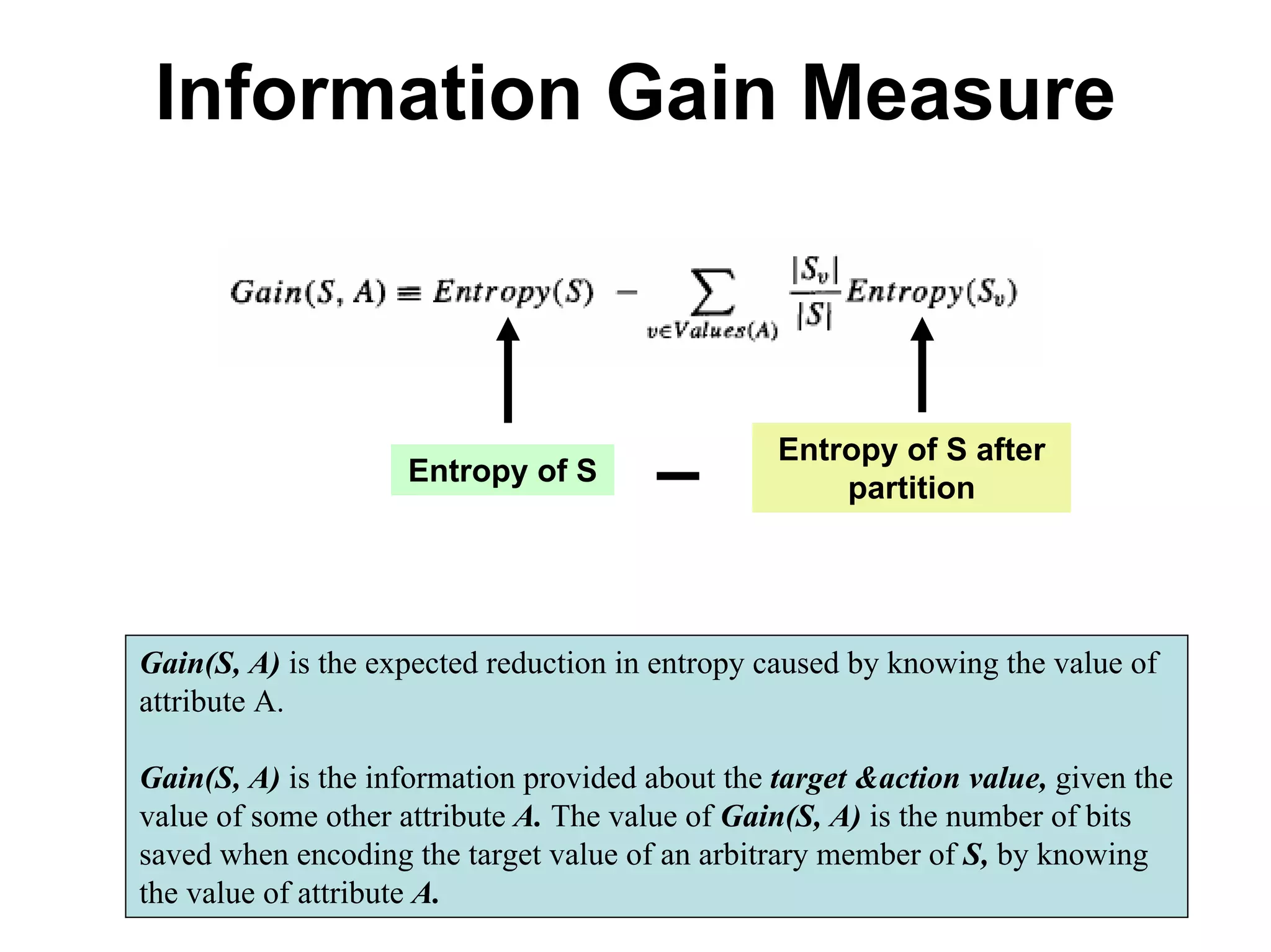
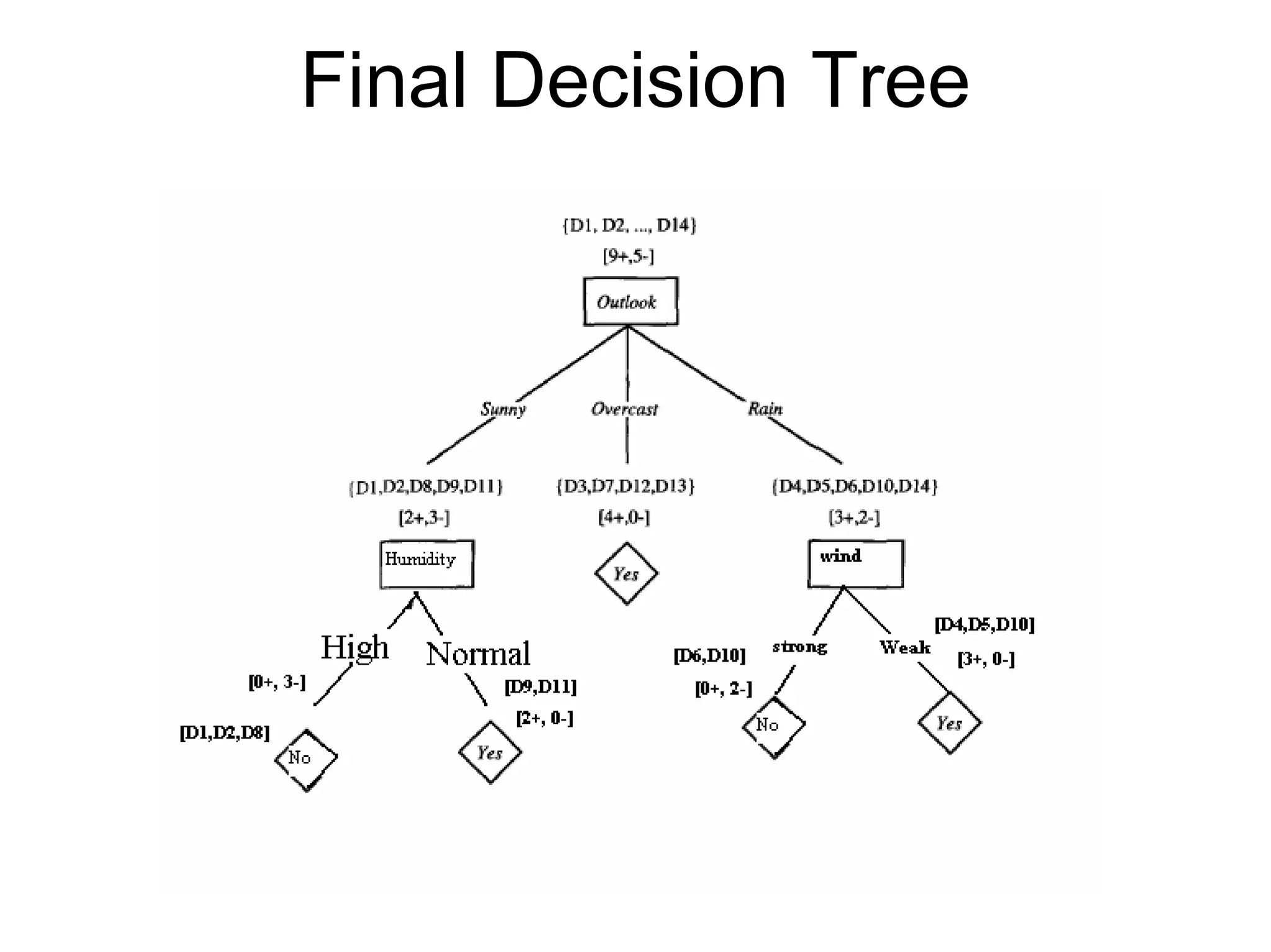
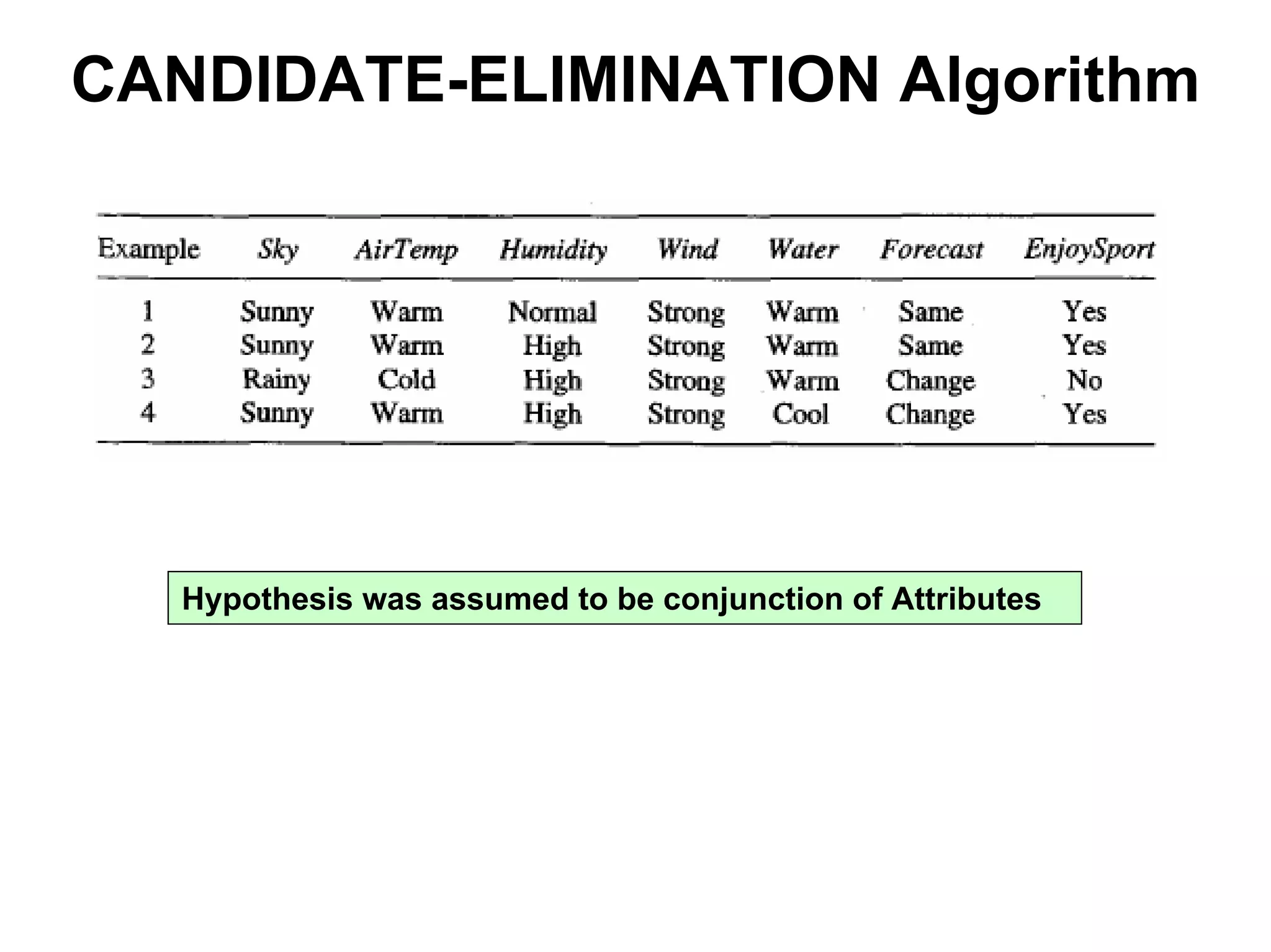
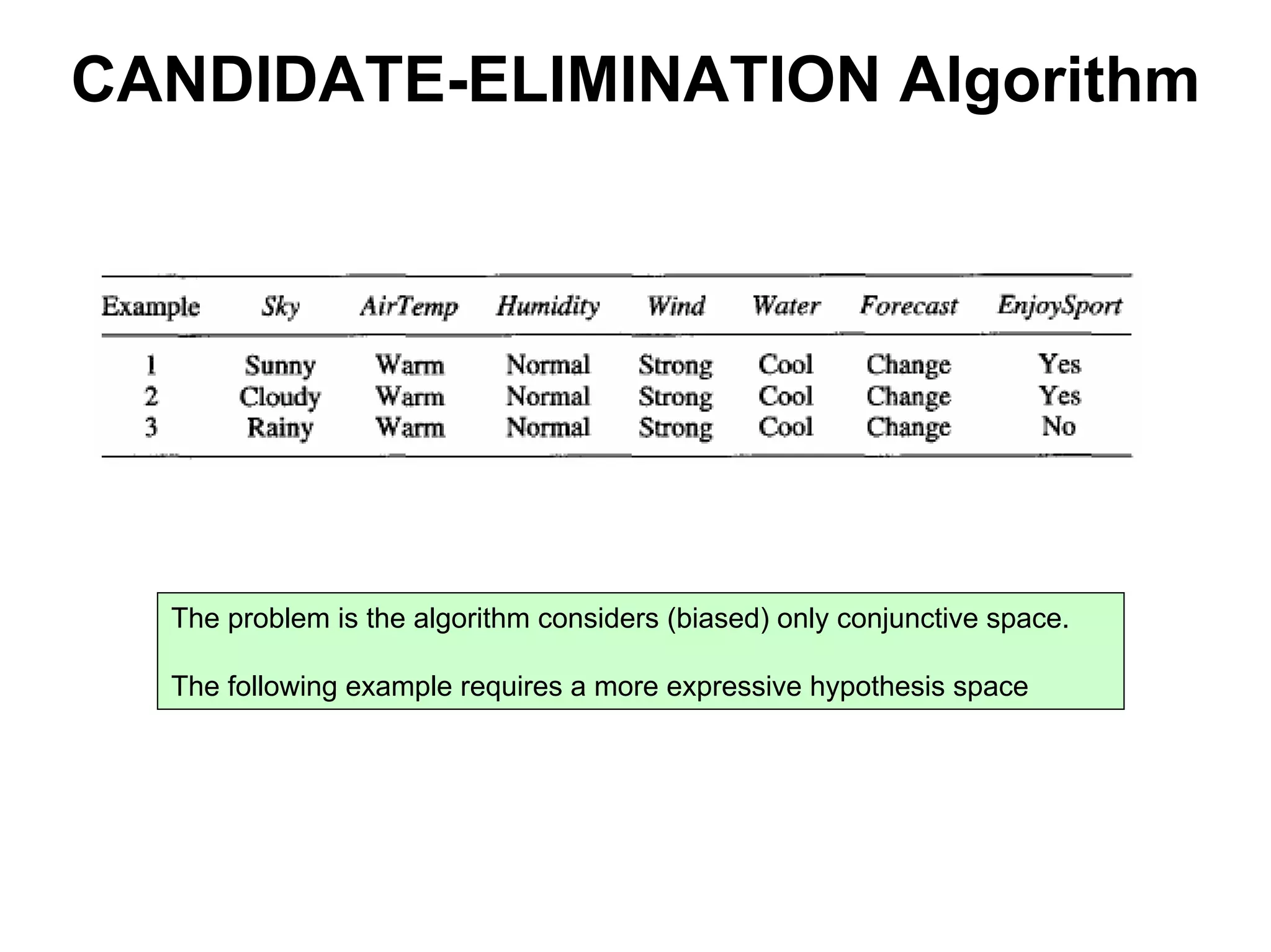
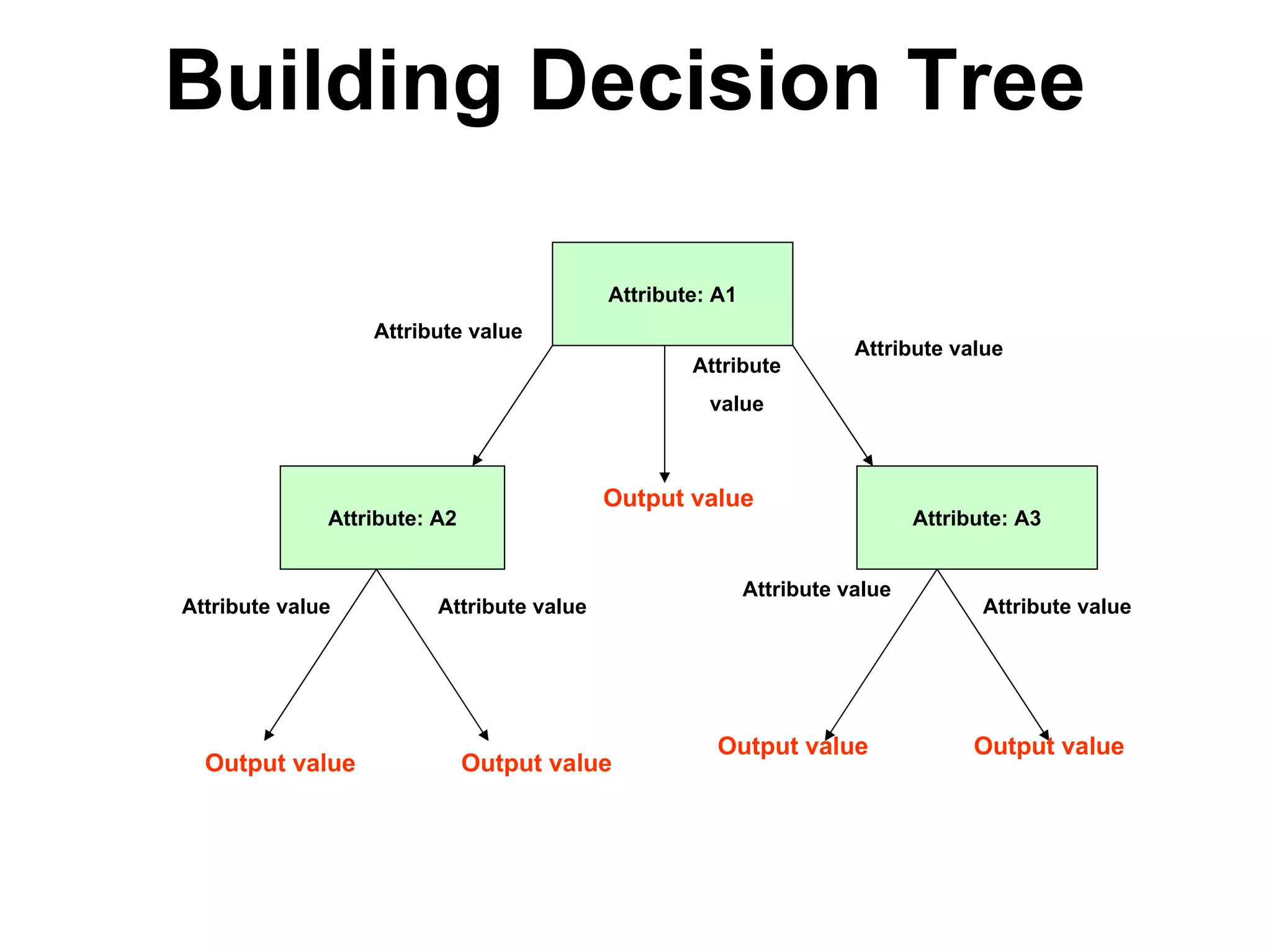
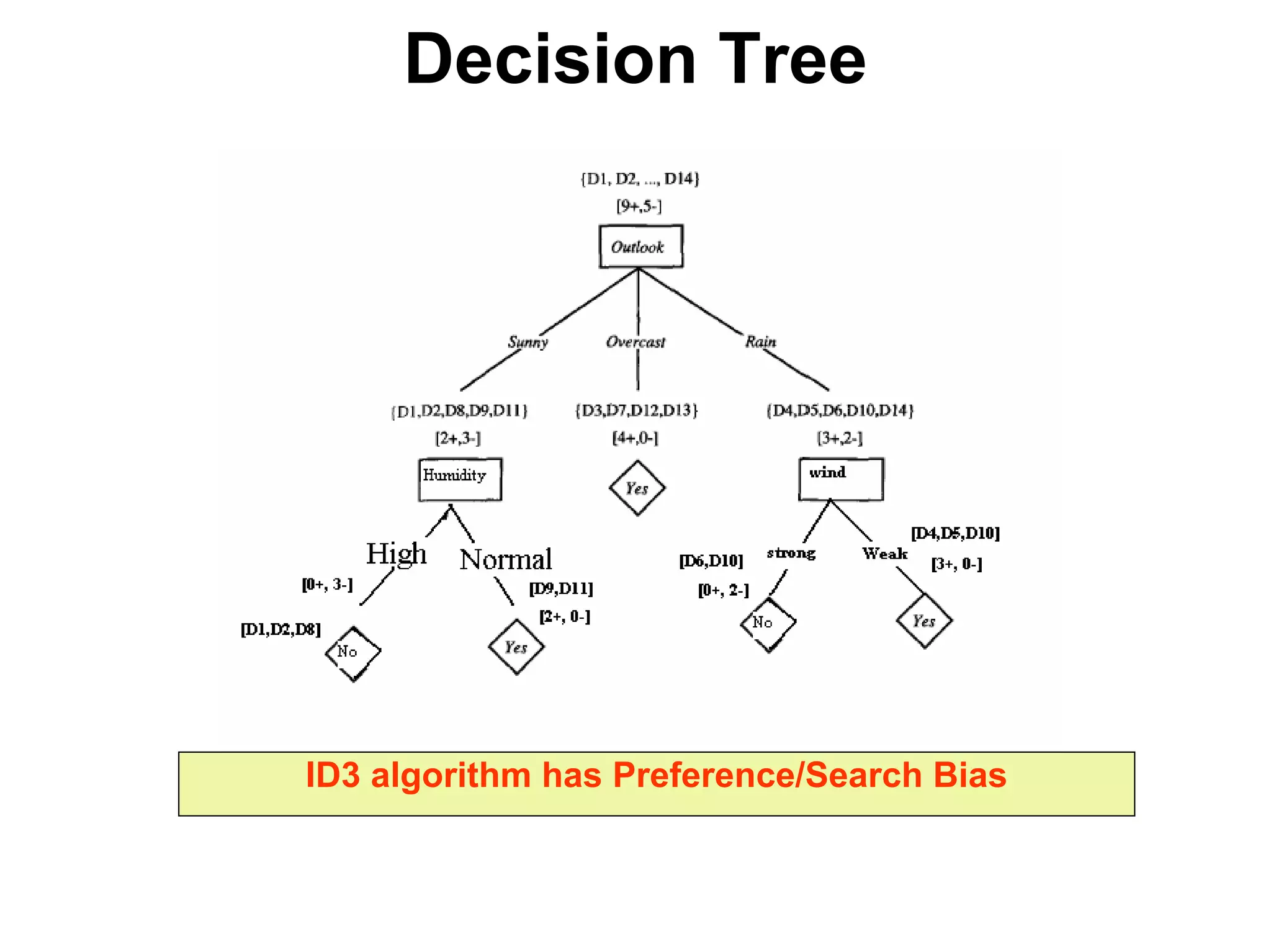
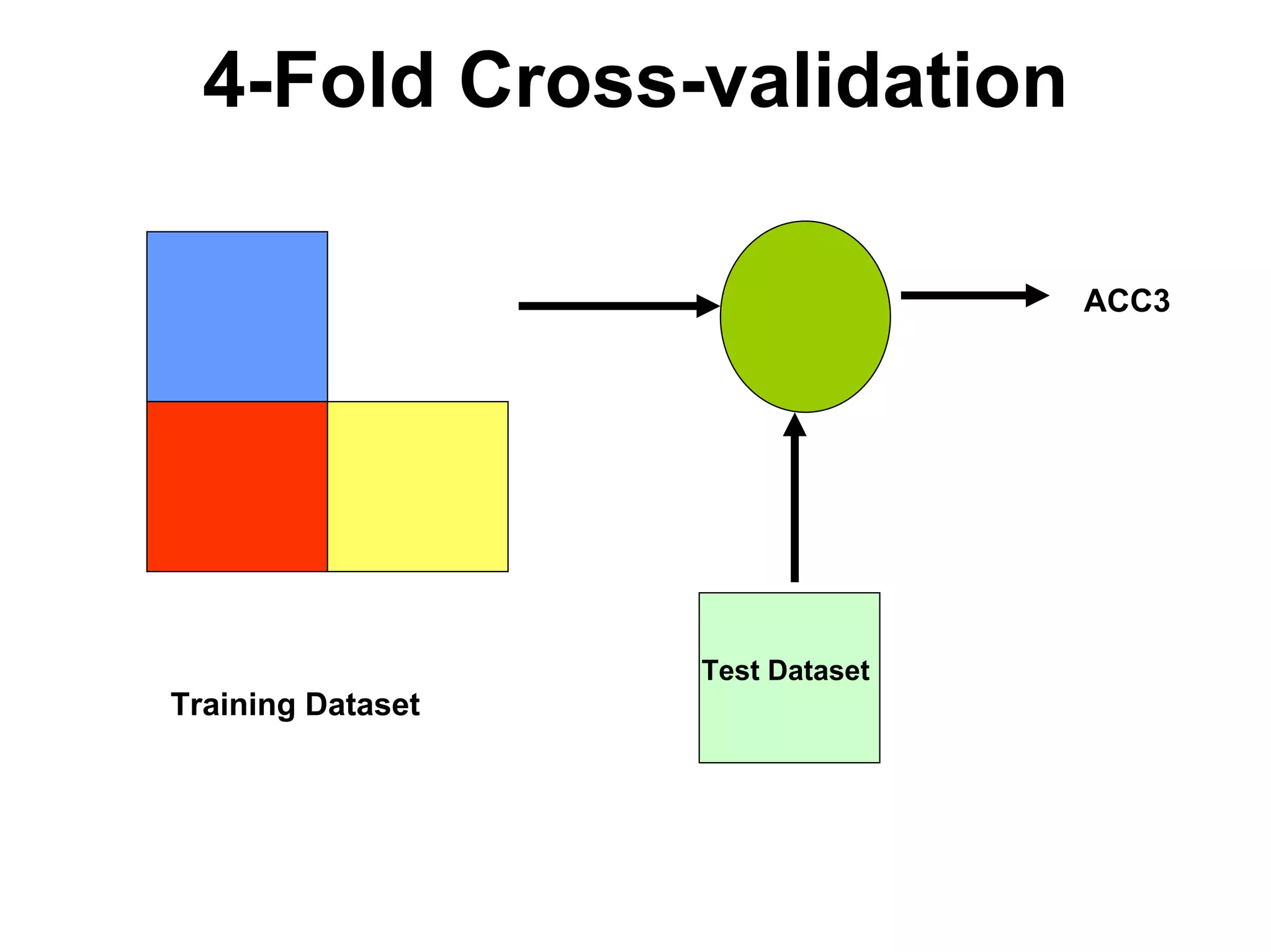
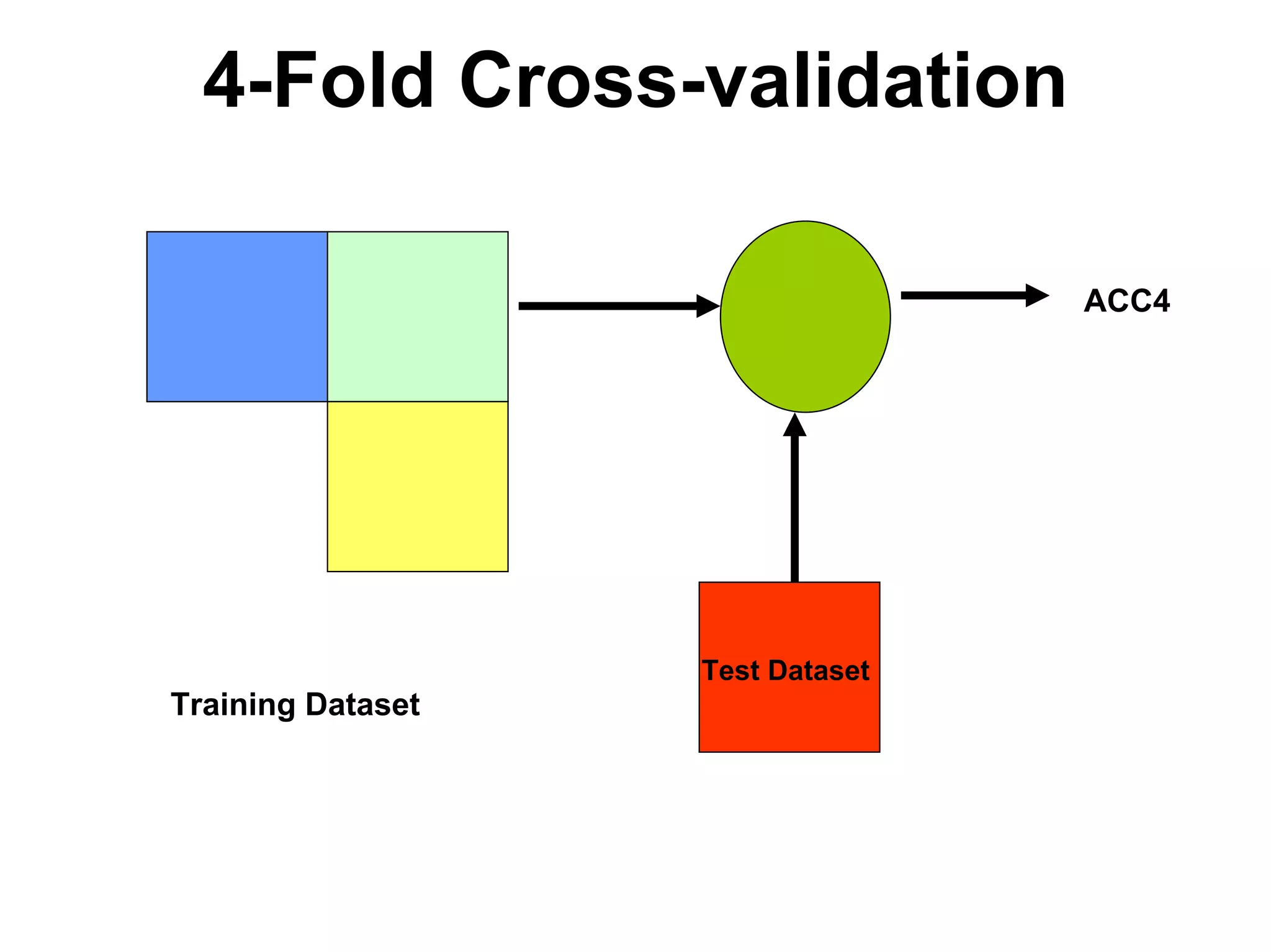
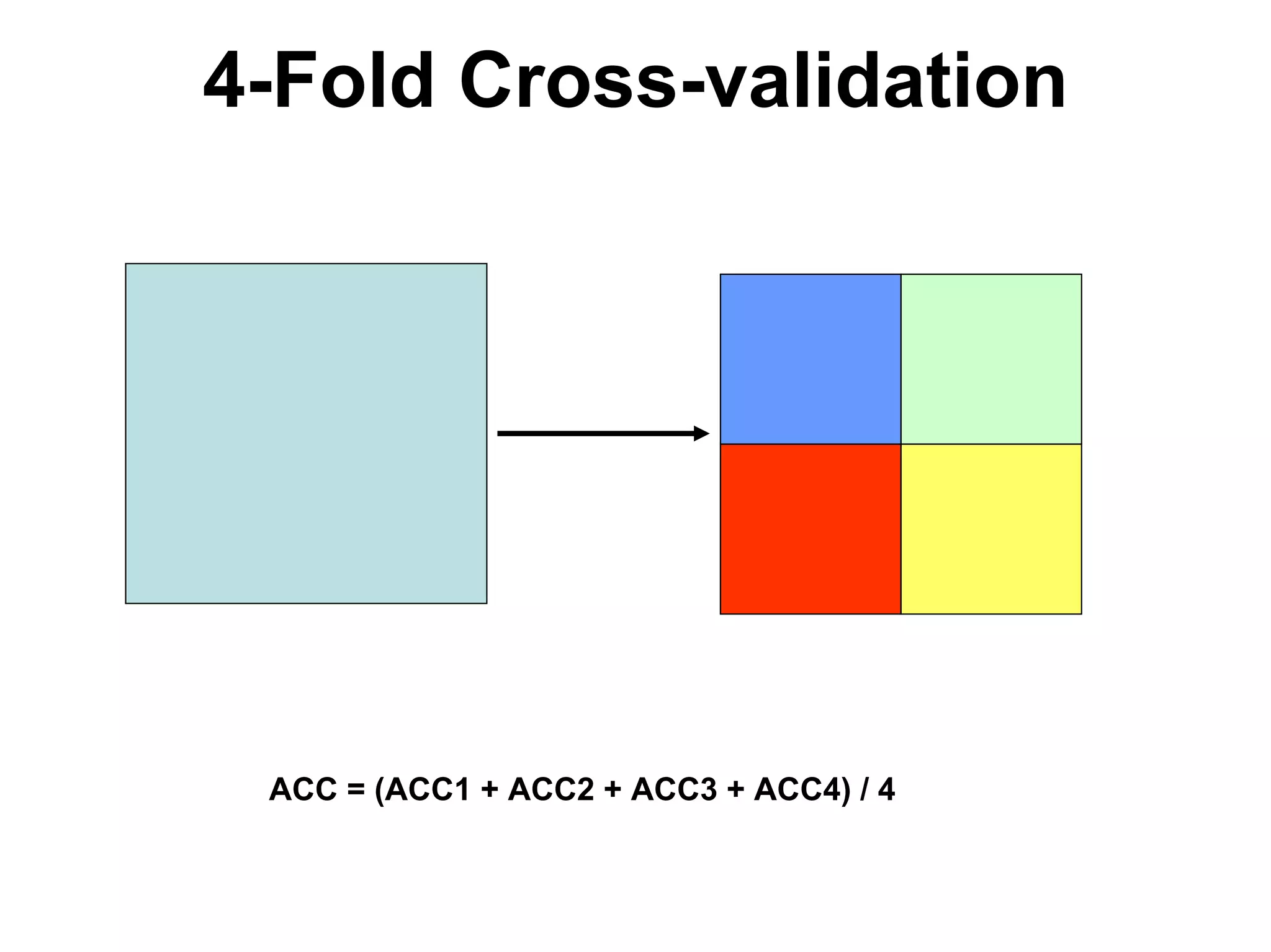
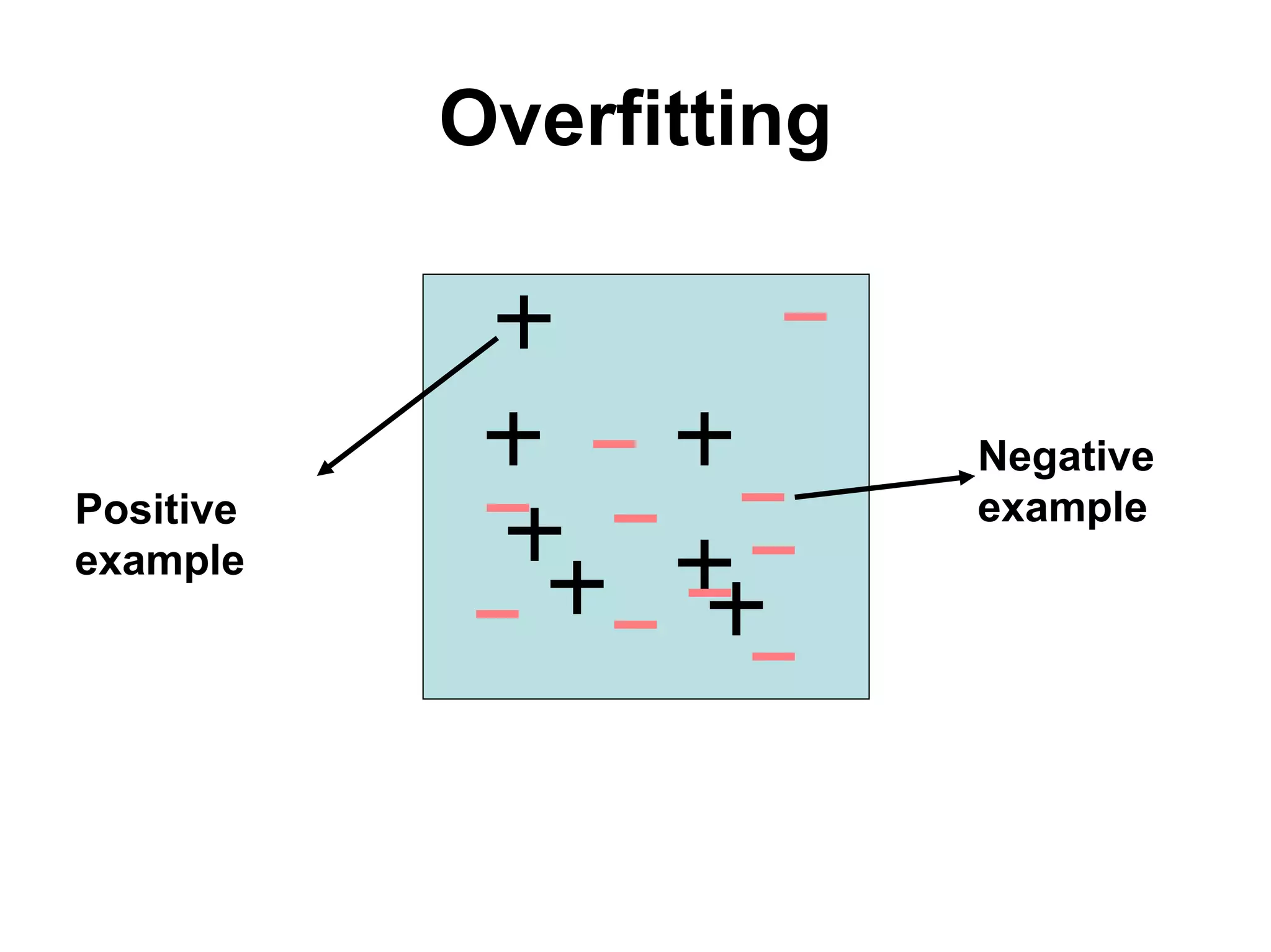
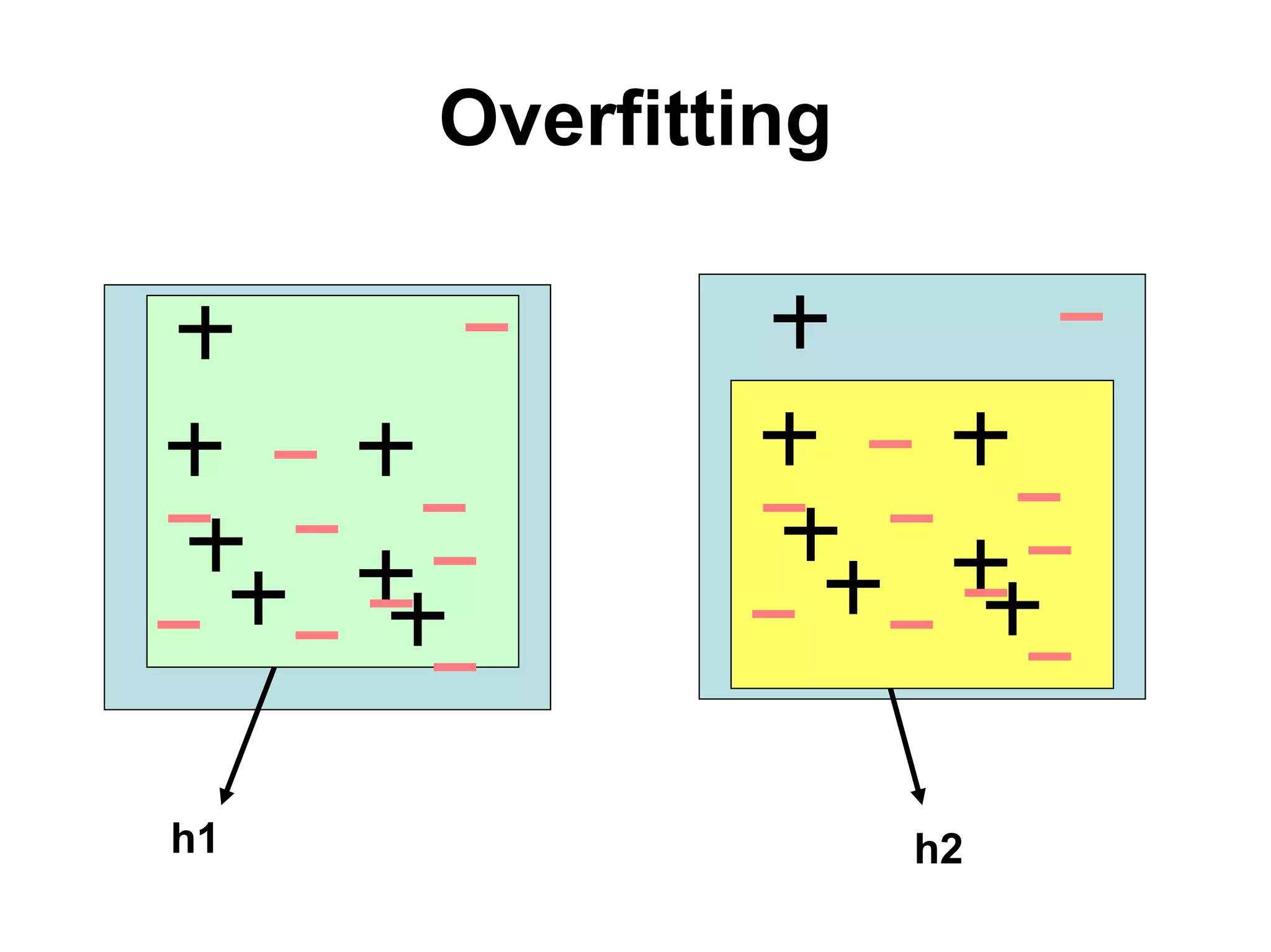
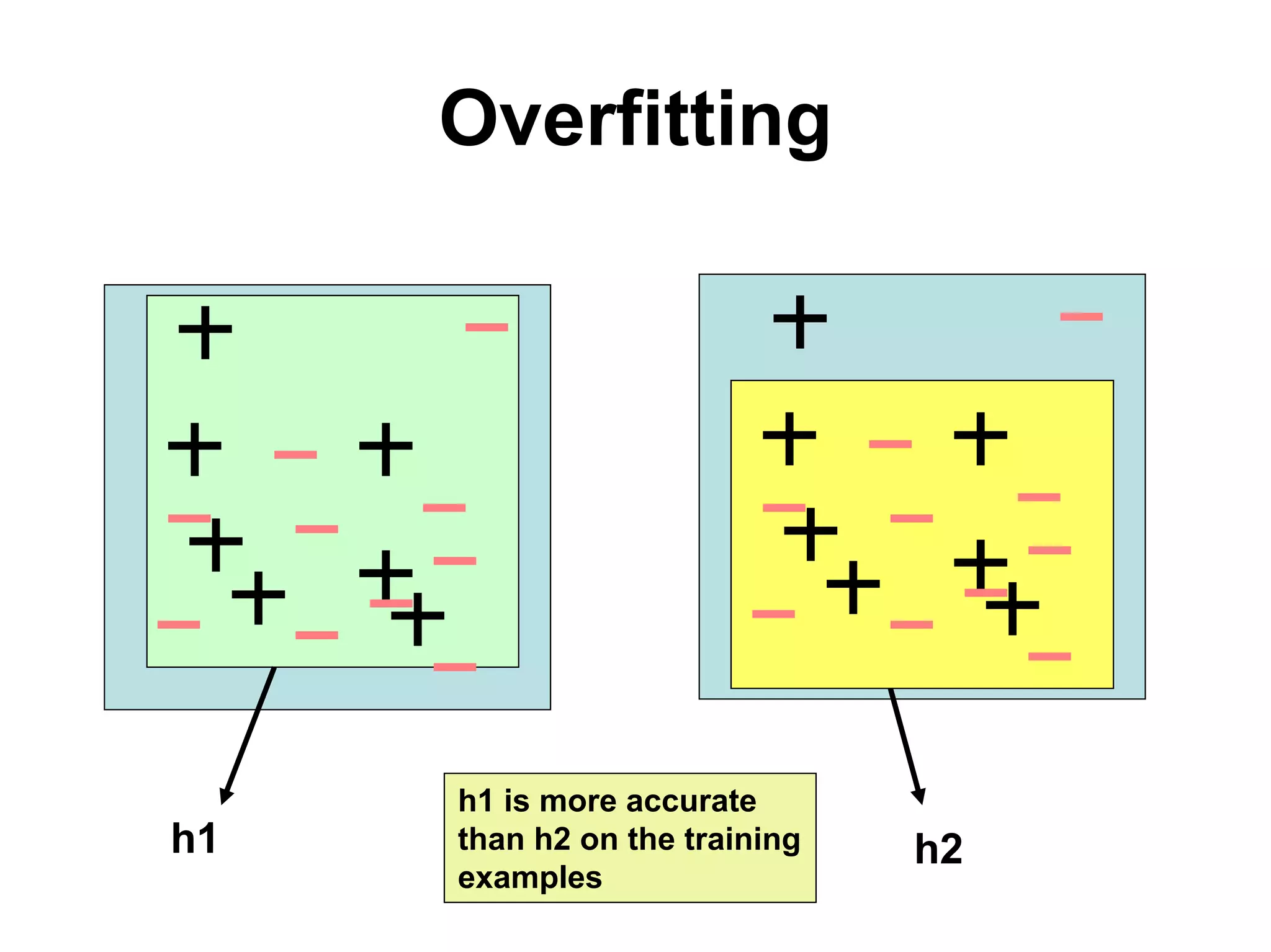
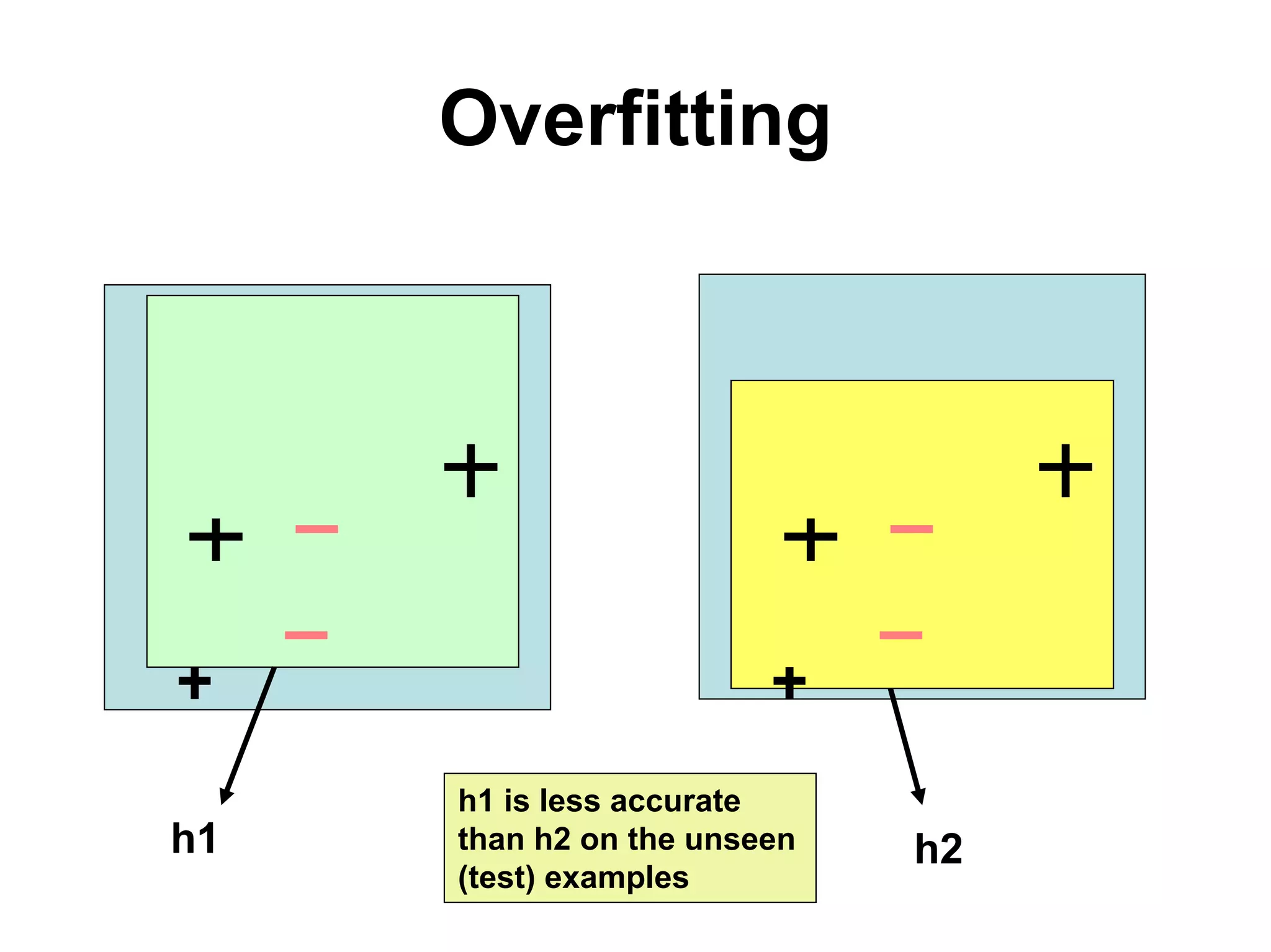
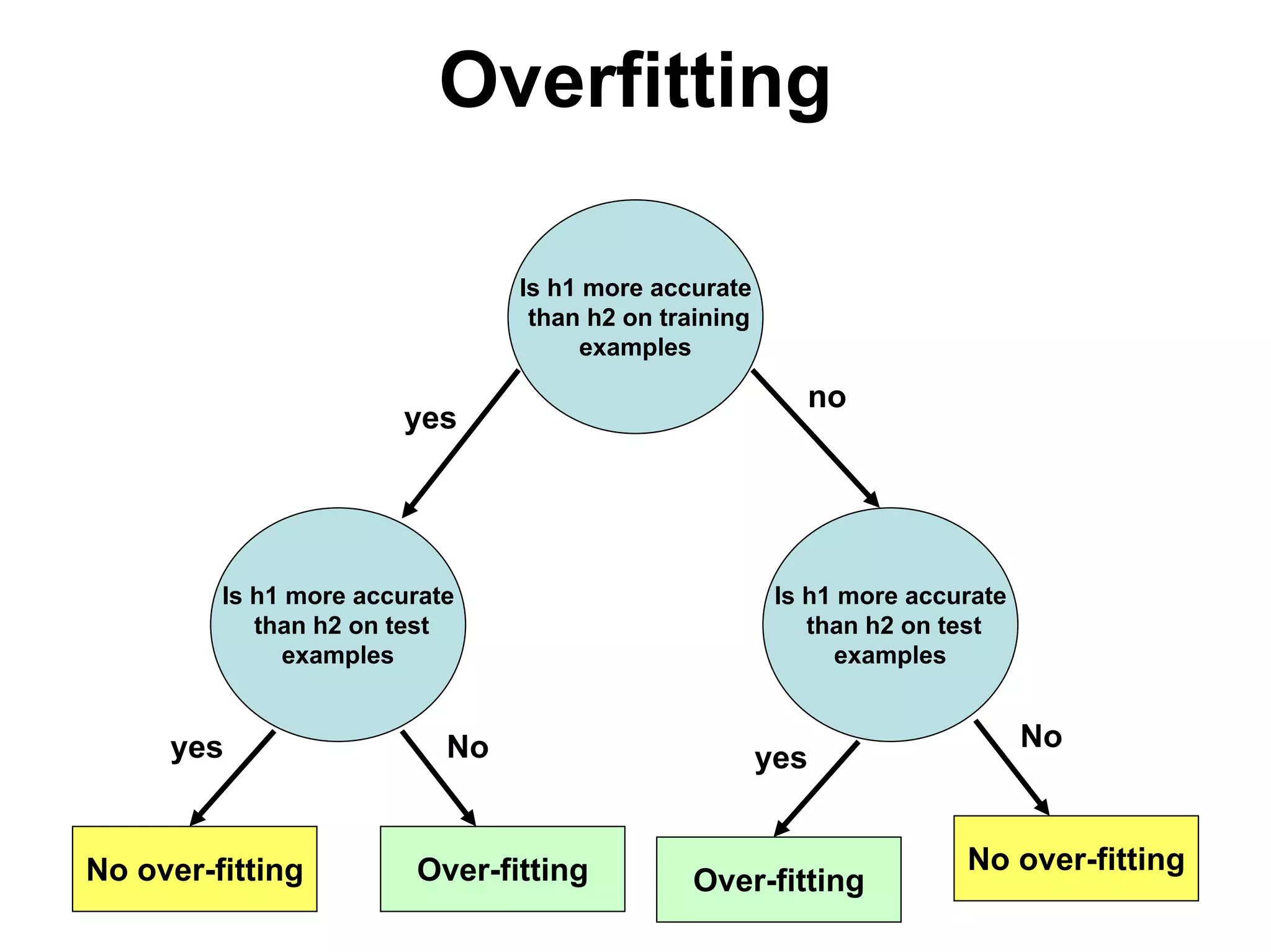
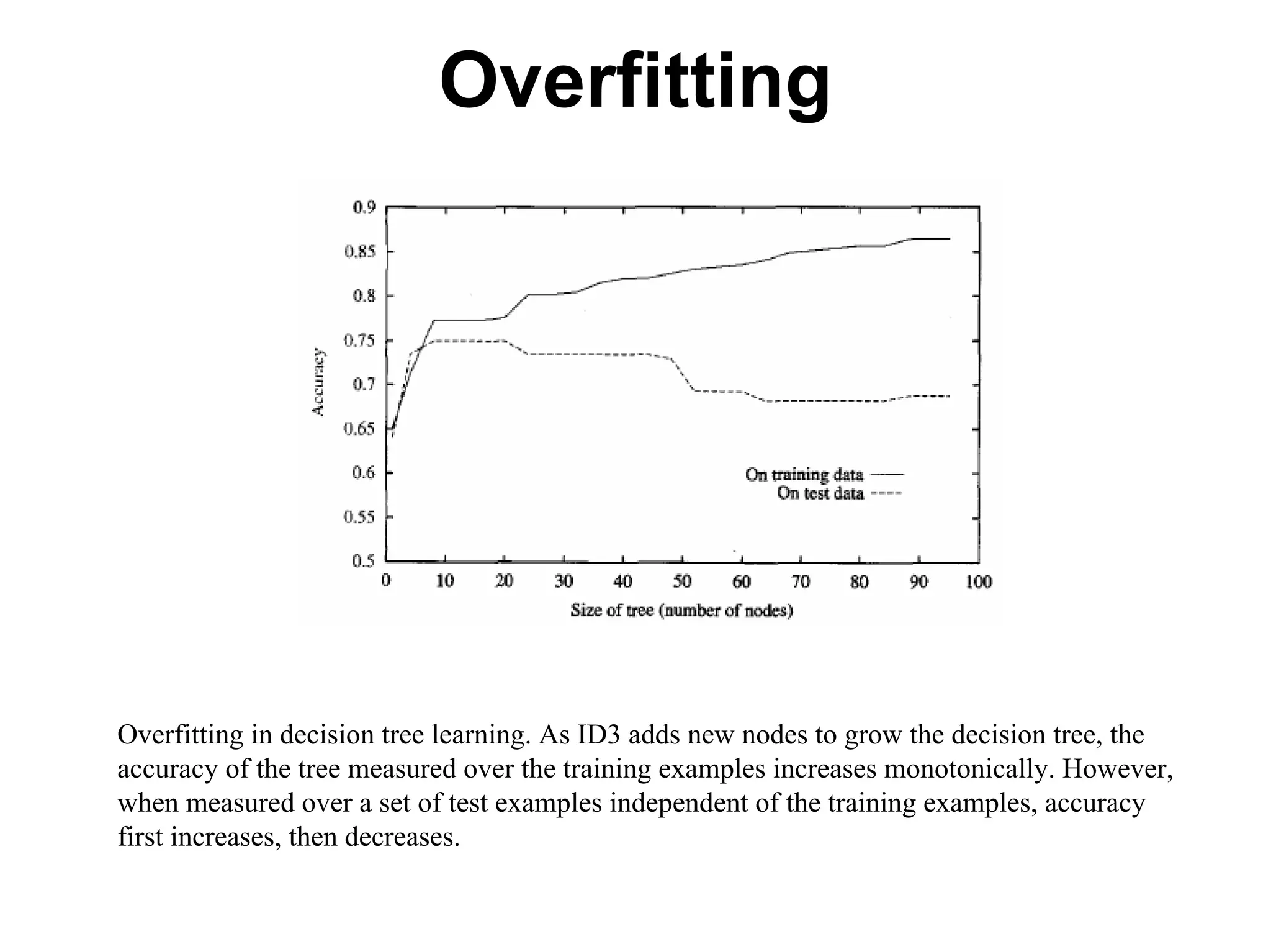
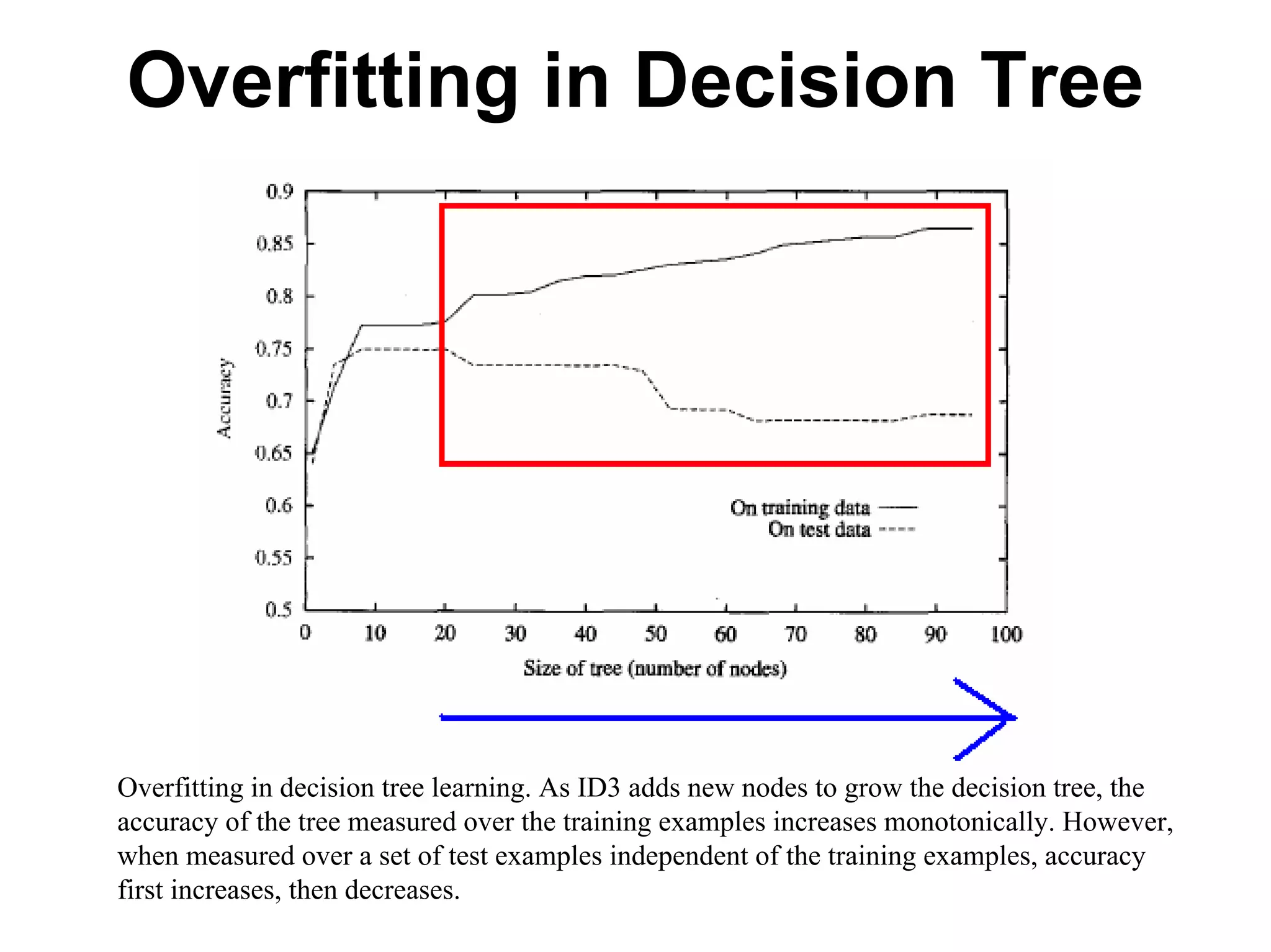
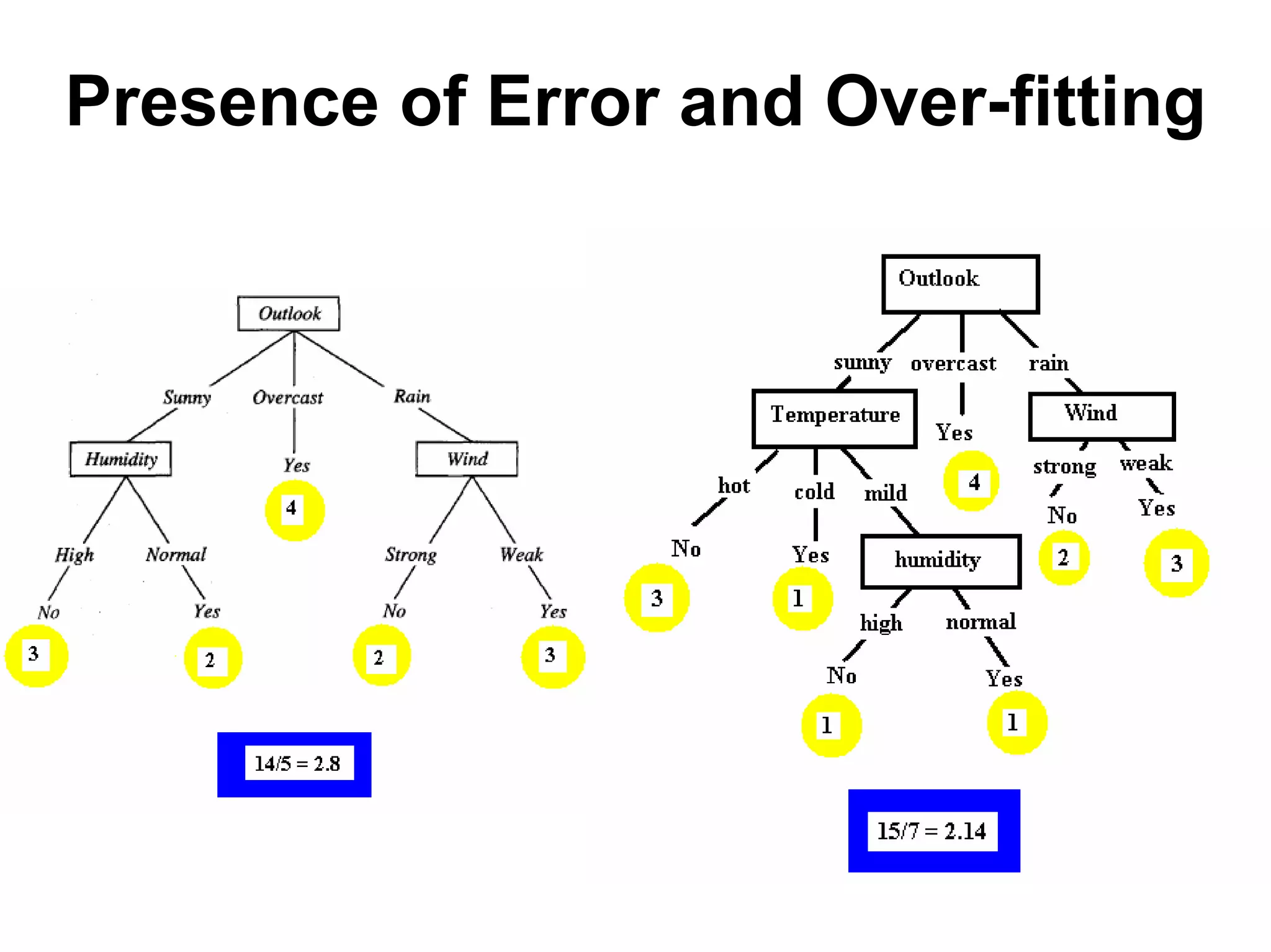
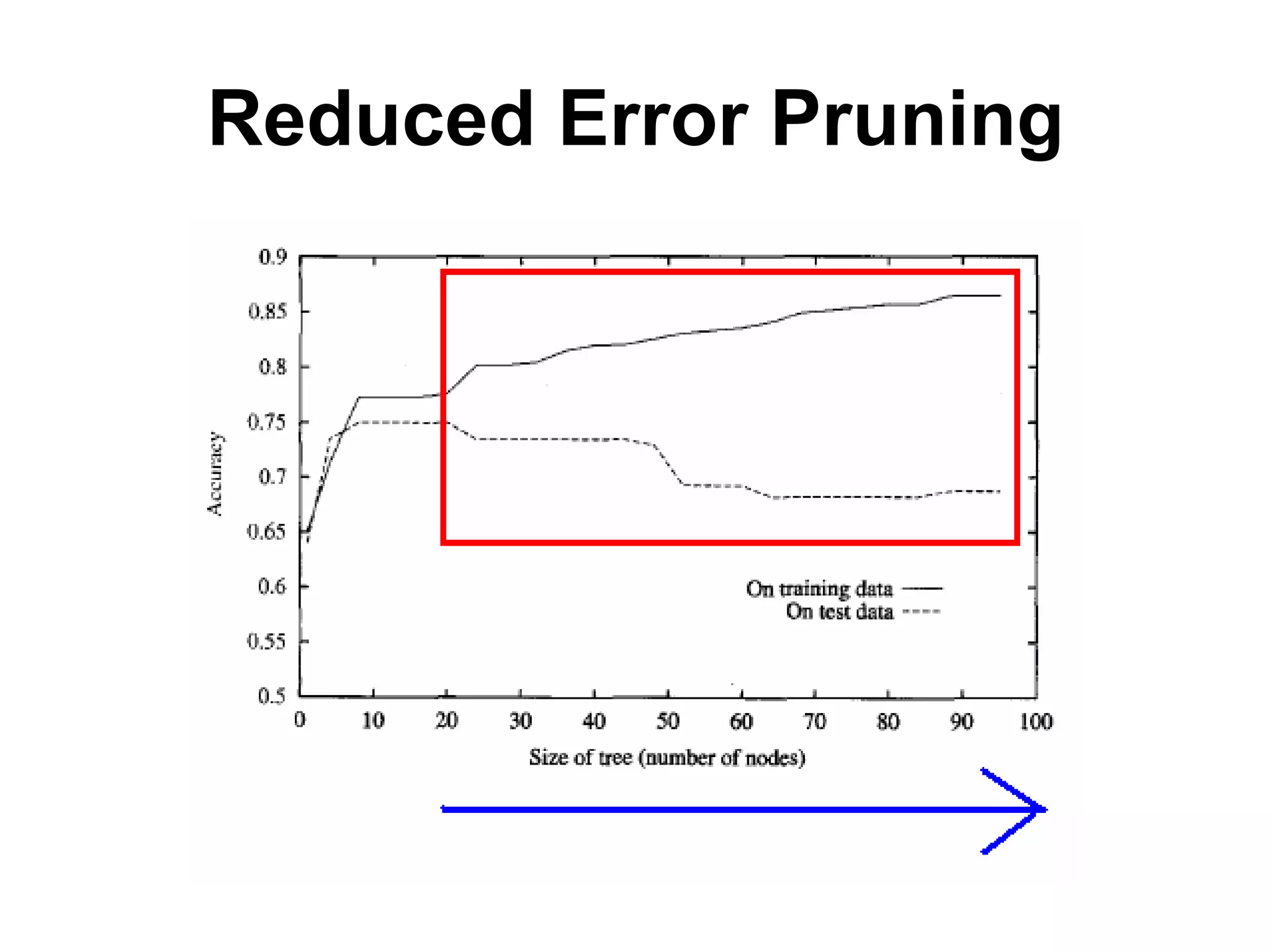
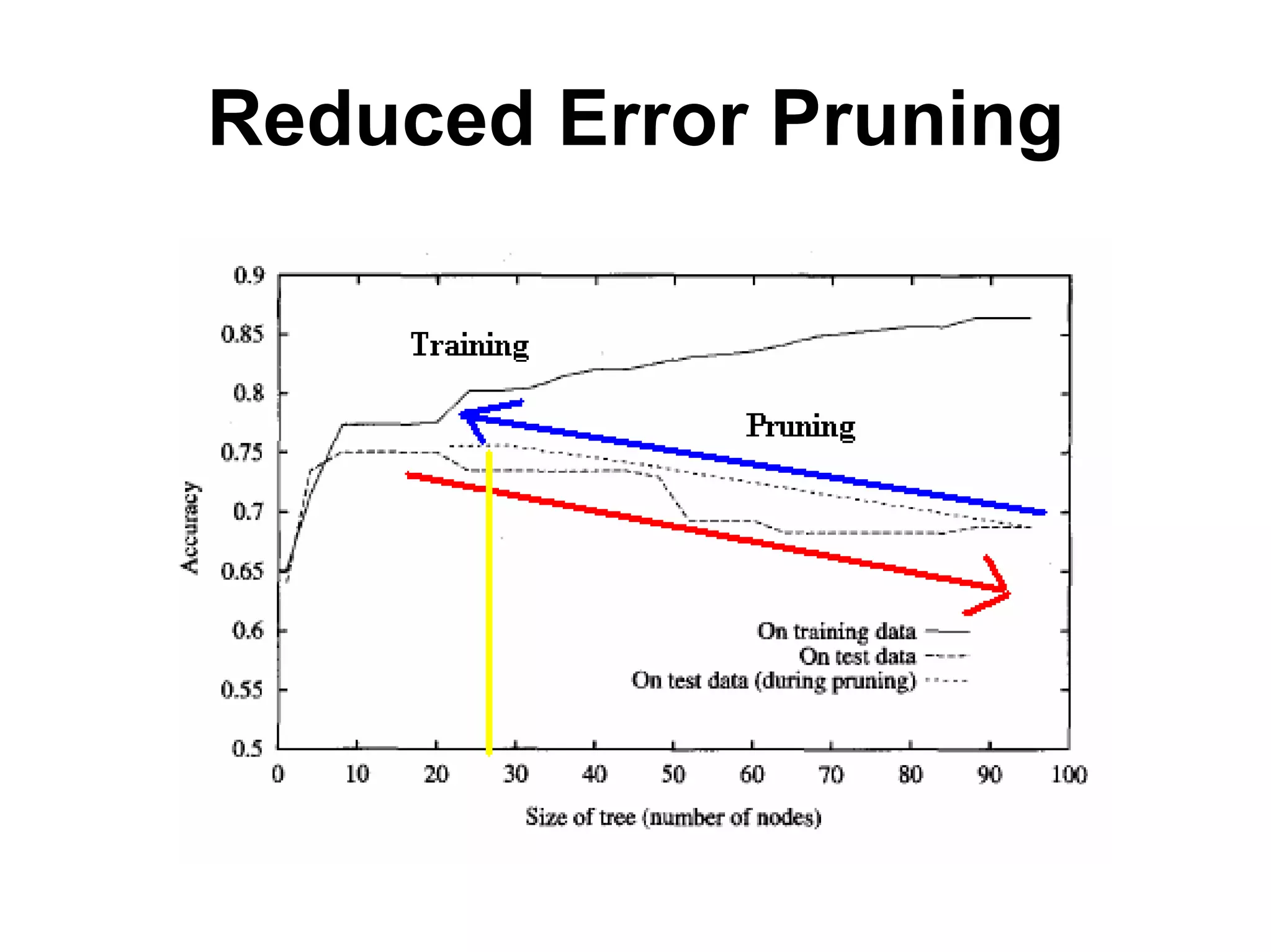
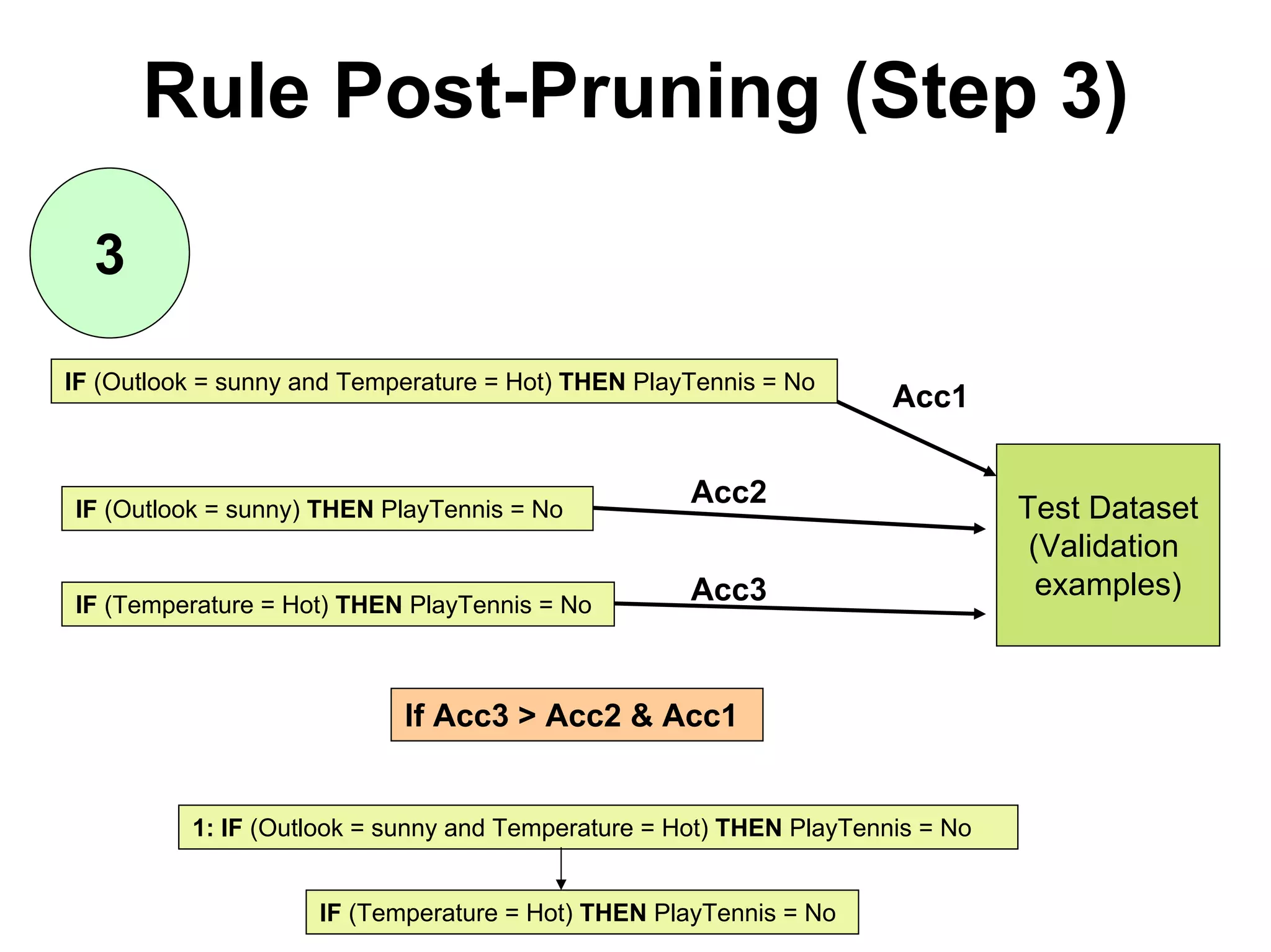
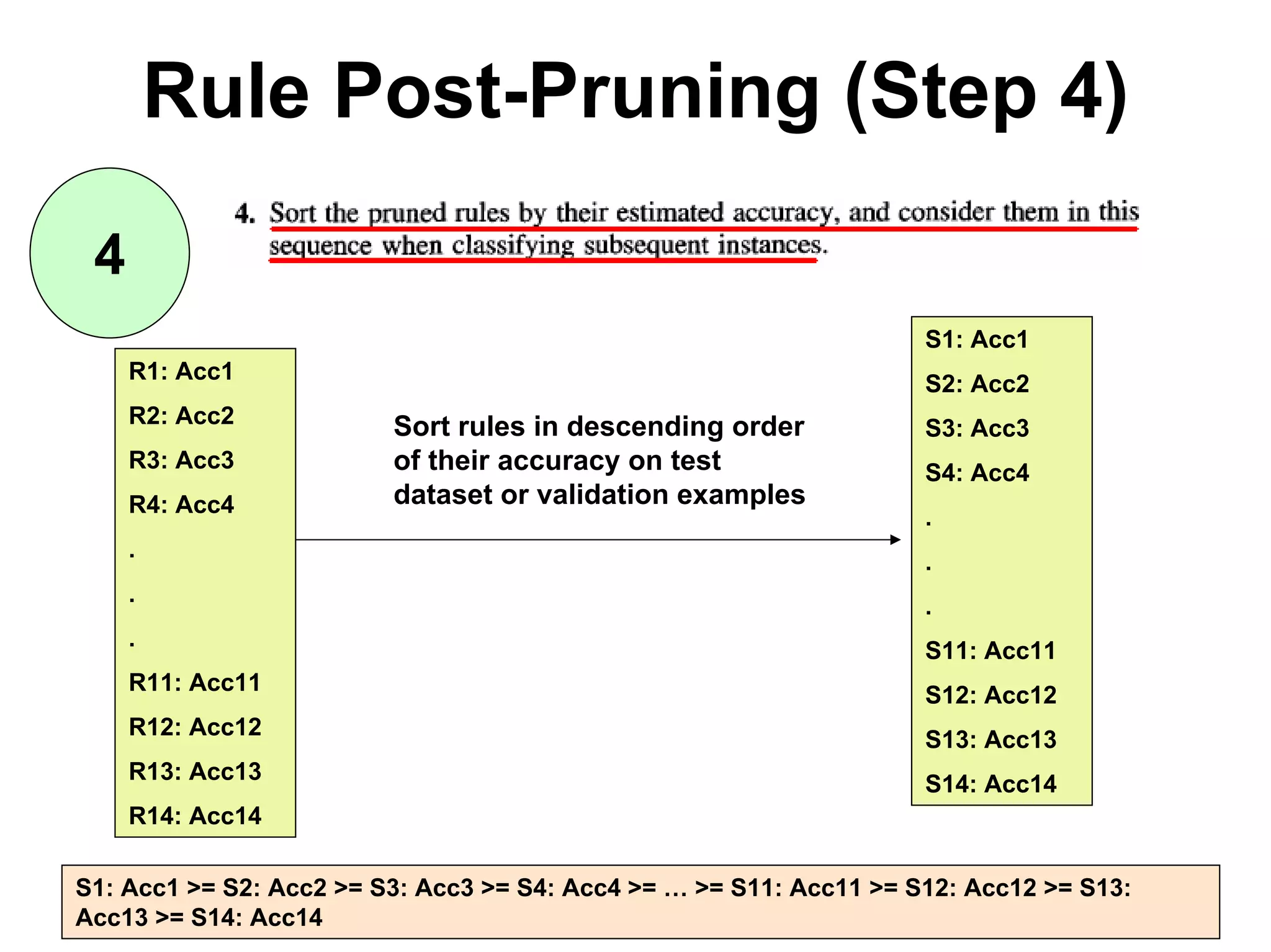
The document discusses a lecture on machine learning algorithms. It covers recapping the ID3 algorithm, machine learning biases including language bias and preference bias, and decision tree learning. It also compares the ID3 and CANDIDATE-ELIMINATION algorithms, noting that ID3 has a preference bias while CANDIDATE-ELIMINATION has a restriction bias.
