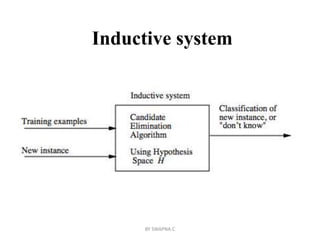
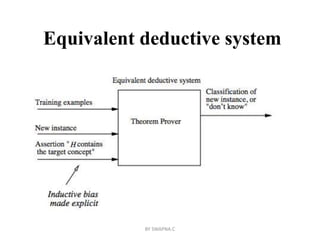
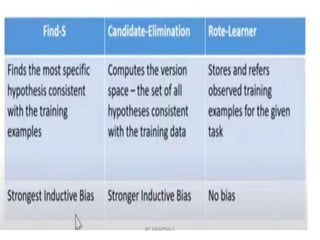
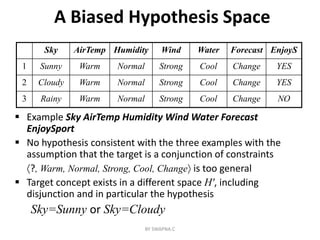
This document discusses inductive bias in machine learning. It defines inductive bias as the assumptions that allow an inductive learning system to generalize beyond its training data. Without some biases, a learning system cannot rationally classify new examples. The document compares different learning algorithms based on the strength of their inductive biases, from weak biases like rote learning to stronger biases like preferring more specific hypotheses. It argues that all inductive learning systems require some inductive biases to generalize at all.

1. INDUCTIVE BIAS
Swapna.C
Asst.Prof.
IT Dept.
Sridevi Women’s Engineering College

2. INDUCTIVE BIAS
• What if the target concept is not contained in the hypothesis
space?
• Can we avoid this difficulty by using a hypothesis space that
includes every possible hypothesis? How does the size of this
hypothesis space influence the ability of the algorithm to
generalize to unobserved instances?
• How does the size of the hypothesis space influence the
number of training examples that must be observed?
• These are fundamental questions for inductive inference in
general. Here we examine them in the context of the
CANDIDATE-ELIMINATION Algorithm. As we shall see,
though, the conclusions we draw from this analysis will apply
to any concept learning system that outputs any hypothesis
consistent with the training data.
BY SWAPNA.C

3. Inductive Bias
• Need to make assumptions
-Experience alone doesn’t allow us to make
conclusions about unseen data instances.
Two types of bias:
-Restriction: Limit the hypothesis space.
-Preference: Impose ordering on hypothesis
space.
BY SWAPNA.C

4. A Biased Hypothesis Space
 Example Sky AirTemp Humidity Wind Water Forecast
EnjoySport
 No hypothesis consistent with the three examples with the
assumption that the target is a conjunction of constraints
?, Warm, Normal, Strong, Cool, Change is too general
 Target concept exists in a different space H', including
disjunction and in particular the hypothesis
Sky=Sunny or Sky=Cloudy
Sky AirTemp Humidity Wind Water Forecast EnjoyS
1 Sunny Warm Normal Strong Cool Change YES
2 Cloudy Warm Normal Strong Cool Change YES
3 Rainy Warm Normal Strong Cool Change NO
BY SWAPNA.C

5. An Unbiased Learner
• The target concept is in the hypothesis space H is to
provide a hypothesis space capable of representing
every teachable concept; that is, it is capable of
representing every possible subset of the instances X.
In general, the set of all subsets of a set X is called
the powerset of X.
• In the EnjoySport learning task, for example, the
size of the instance space X of days described by the
six available attributes is 96. How many possible
concepts can be defined over this set of instances? In
other words, how large is the power set of X?
BY SWAPNA.C

6. In general, the number of distinct subsets that
can be defined over a set X containing
|X|elements (i.e., the size of the power set of
X) is2^|X| . Thus, there are 2^96, or
approximately 10^28 distinct target concepts
that could be defined over this instance space
and that our learner might be called upon to
learn.
• our conjunctive hypothesis space is able to
represent only 973 of these-a very biased
hypothesis space indeed!
BY SWAPNA.C

7. • Ex: Enjoysport learning task.
• H' correspond to the power set of X.
• For instance, the target concept "Sky = Sunny
or Sky = Cloudy" could then be described as
• (Sunny, ?, ?, ?, ?, ?) v (Cloudy, ?, ?, ?, ?, ?)
• we present three positive examples (x1, x2, x3)
and two negative examples (x4, x5) to the
learner. At this point, the S boundary of the
version space will contain the hypothesis
which is just the disjunction of the positive
examples because this is the most specific
possible hypothesis that covers these three
examples.
BY SWAPNA.C

8. • Similarly, the G boundary will consist of the
hypothesis that rules out only the observed
negative examples
• The problem here is that with this very
expressive hypothesis representation, the S
boundary will always be simply the
disjunction of the observed positive examples,
while the G boundary will always be the
negated disjunction of the observed negative
examples.
BY SWAPNA.C

9. No generalization without bias!
• VS after presenting three positive instances x1, x2, x3, and two
negative instances x4, x5
S = {(x1 v x2 v x3)}
G = {¬(x4 v x5)}
… all subsets including x1 x2 x3 and not including x4 x5
• We can only classify precisely examples already seen!
• Take a majority vote?
– Unseen instances, e.g. x, are classified positive (and
negative) by half of the hypothesis
– For any hypothesis h that classifies x as positive, there is a
complementary hypothesis ¬h that classifies x as negative
BY SWAPNA.C

10. The Futility of Bias-Free Learning
• A fundamental property of inductive inference:
a learner that makes no a priori assumptions
regarding the identity of the target concept has
no rational basis for classifying any unseen
instances.
• The key idea we wish to capture here is the
policy by which the learner generalizes beyond
the observed training data, to infer the
classification of new instances.
BY SWAPNA.C

11. • Therefore, consider the general setting in
which an arbitrary learning algorithm L is
provided an arbitrary set of training data D, =
{(x, c(x))} of some arbitrary target concept c.
After training, L is asked to classify a new
instance xi.
• Let L(xi, D,) denote the classification (e.g.,
positive or negative) that L assigns to xi after
learning from the training data D, We can
describe this inductive inference step
performed by L as follows where the notation
y |-- z indicates that z is inductively inferred
from y.
BY SWAPNA.C

12. • we define the inductive bias of L to be the set
of assumptions B such that for all new
instances xi (B ^ D ^ xi) |- L(xi, D)
• where the notation y |- z indicates that z
follows deductively from y (i.e., that z
is provable from y). Thus, we define the
inductive bias of a learner as the set of
additional assumptions B sufficient to justify
its inductive inferences as deductive
inferences.
BY SWAPNA.C

13. Inductive bias: definition
• Given:
– a concept learning algorithm L for a set of instances X
– a concept c defined over X
– a set of training examples for c: Dc = {x, c(x)}
– L(xi, Dc) outcome of classification of xi after learning
• Inductive inference ( ≻ ):
Dc  xi ≻ L(xi, Dc)
• The inductive bias is defined as a minimal set of assumptions
B, such that (|− for deduction)
 (xi  X) [ (B  Dc  xi) |− L(xi, Dc) ]
BY SWAPNA.C

14. Inductive and Deductive Reasoning
Inductive Reasoning
• Specific to General
• Logically true
• May or may not be
realistically true
• Example:
• St1: Mango is fruit(Specific)
• St2: The box is full of
fruits(Specific)
• Con:The box is full of
mangoes(General)
Deductive Reasoning
• General to Specific
• Logically true
• Realistically true
• Example:
• St1: All mangoes are
fruits.(General)
• St2: All fruits have
seeds.(General)
• Con: Mangoes have
seeds.(Specific)
BY SWAPNA.C

15. Inductive system
BY SWAPNA.C

16. Equivalent deductive system
BY SWAPNA.C

17. Advantages
• One advantage of viewing inductive inference
systems in terms of their inductive bias is that
it provides a nonprocedural means of
characterizing their policy for generalizing
beyond the observed data.
• A second advantage is that it allows
comparison of different learners according to
the strength of the inductive bias they employ.
Consider, for example, the following three
learning algorithms, which are listed from
weakest to strongest bias.
BY SWAPNA.C

18. 1. ROTE-LEARNER: Learning corresponds simply to
storing each observed training example in memory.
Subsequent instances are classified by looking them up
in memory. If the instance is found in memory, the
stored classification is returned. Otherwise, the system
refuses to classify the new instance.
2. CANDIDATE-ELIMINATION Algorithm New
instances are classified only in the case where all
members of the current version space agree on the
classification. Otherwise, the system refuses to classify
the new instance.
3. FIND-S: This algorithm, described earlier, finds the
most specific hypothesis consistent with the training
examples. It then uses this hypothesis to classify all
subsequent instances. BY SWAPNA.C

19. BY SWAPNA.C

20. • The ROTE-LEARNER has no inductive bias. The
classifications it provides for new instances
follow deductively from the observed training
examples, with no additional assumptions
required.
• The CANDIDATE-ELIMINATION Algorithm has a
stronger inductive bias: that the target
concept can be represented in its hypothesis
space.
• The FIND-S algorithm has an even stronger
inductive bias.
BY SWAPNA.C

21. • Some inductive biases correspond to
categorical assumptions that completely rule
out certain concepts, such as the bias "the
hypothesis space H includes the target
concept."
• Other inductive biases merely rank order the
hypotheses by stating preferences such as
"more specific hypotheses are preferred over
more general hypotheses."
BY SWAPNA.C