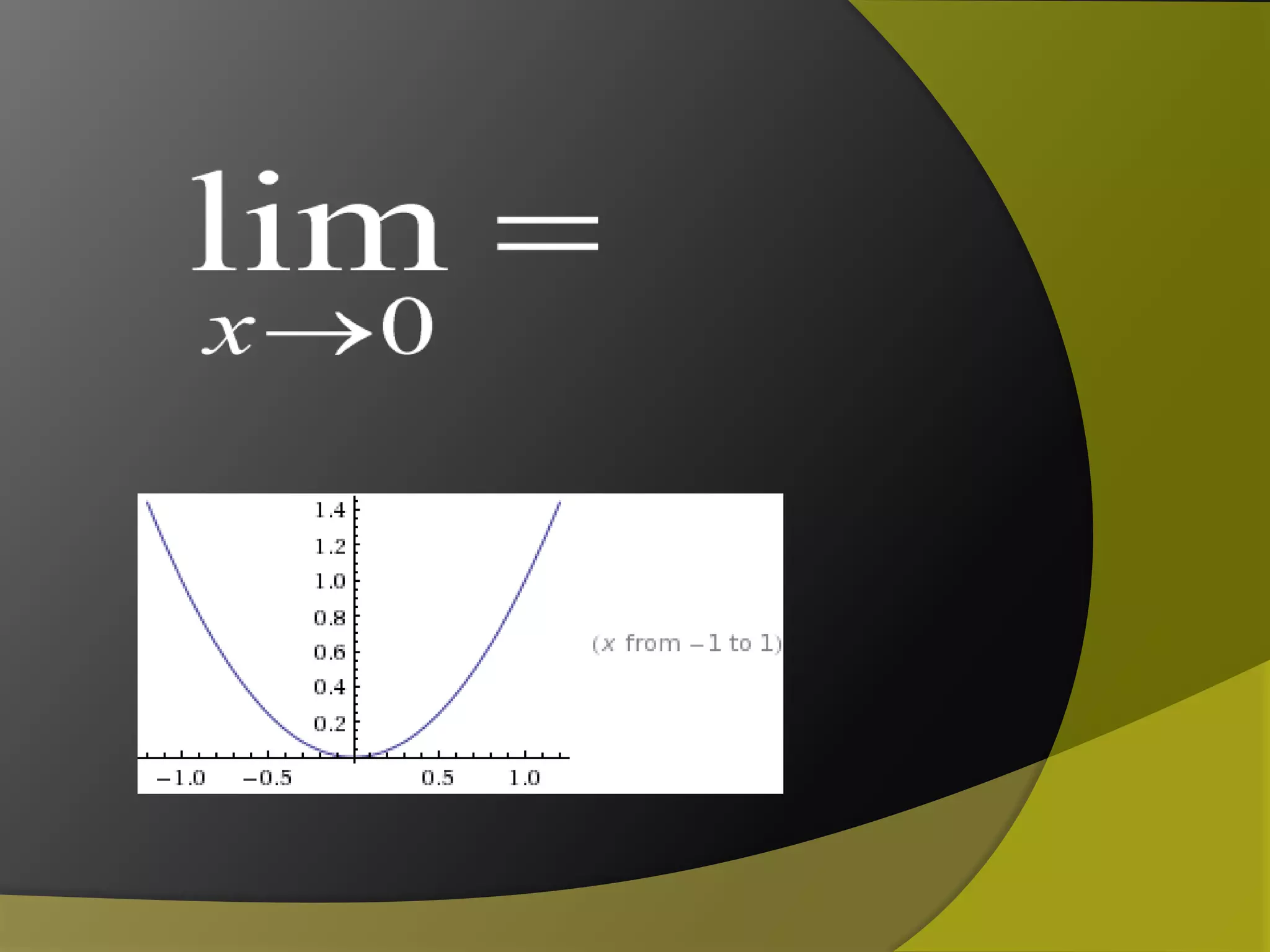
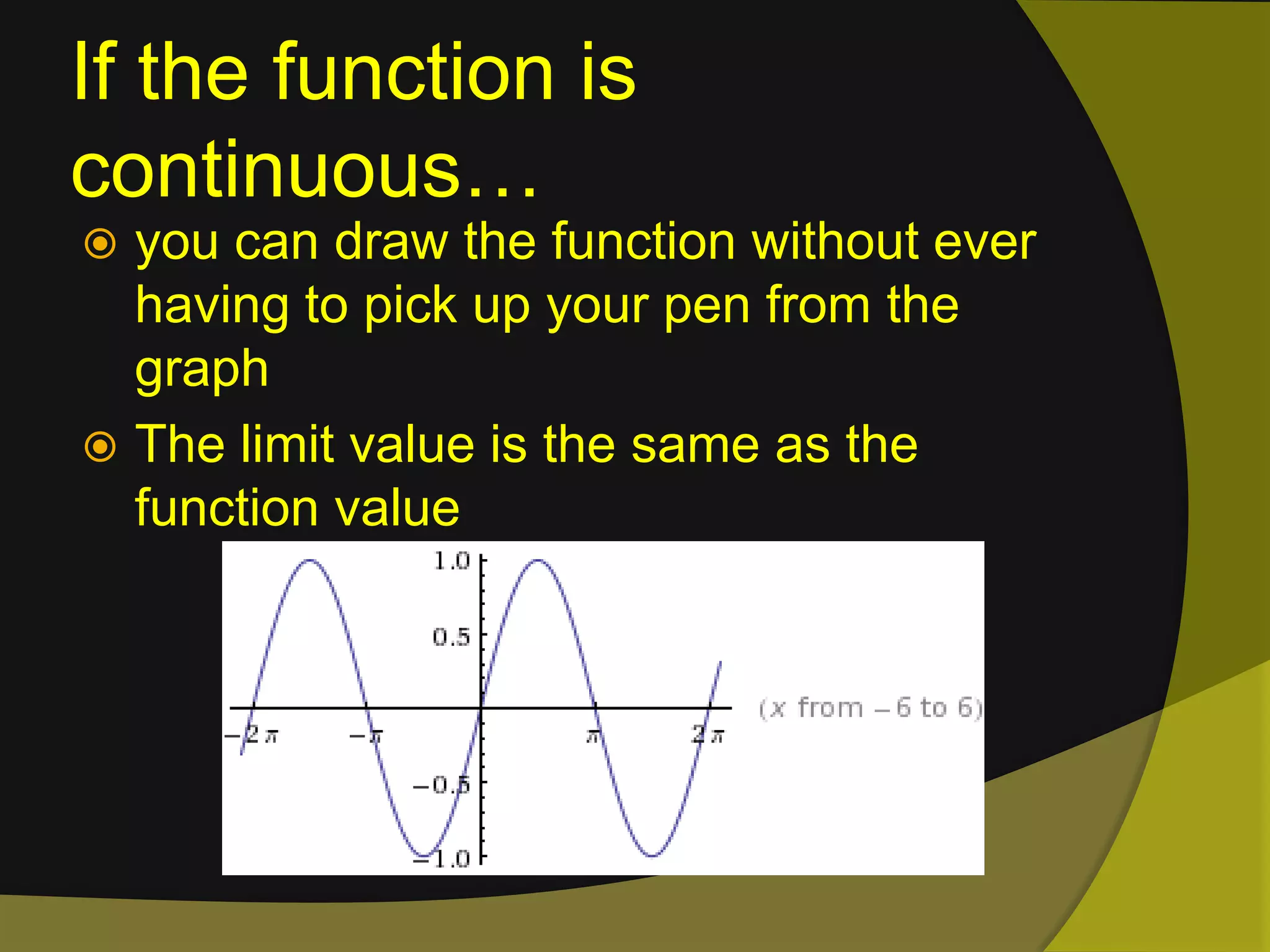
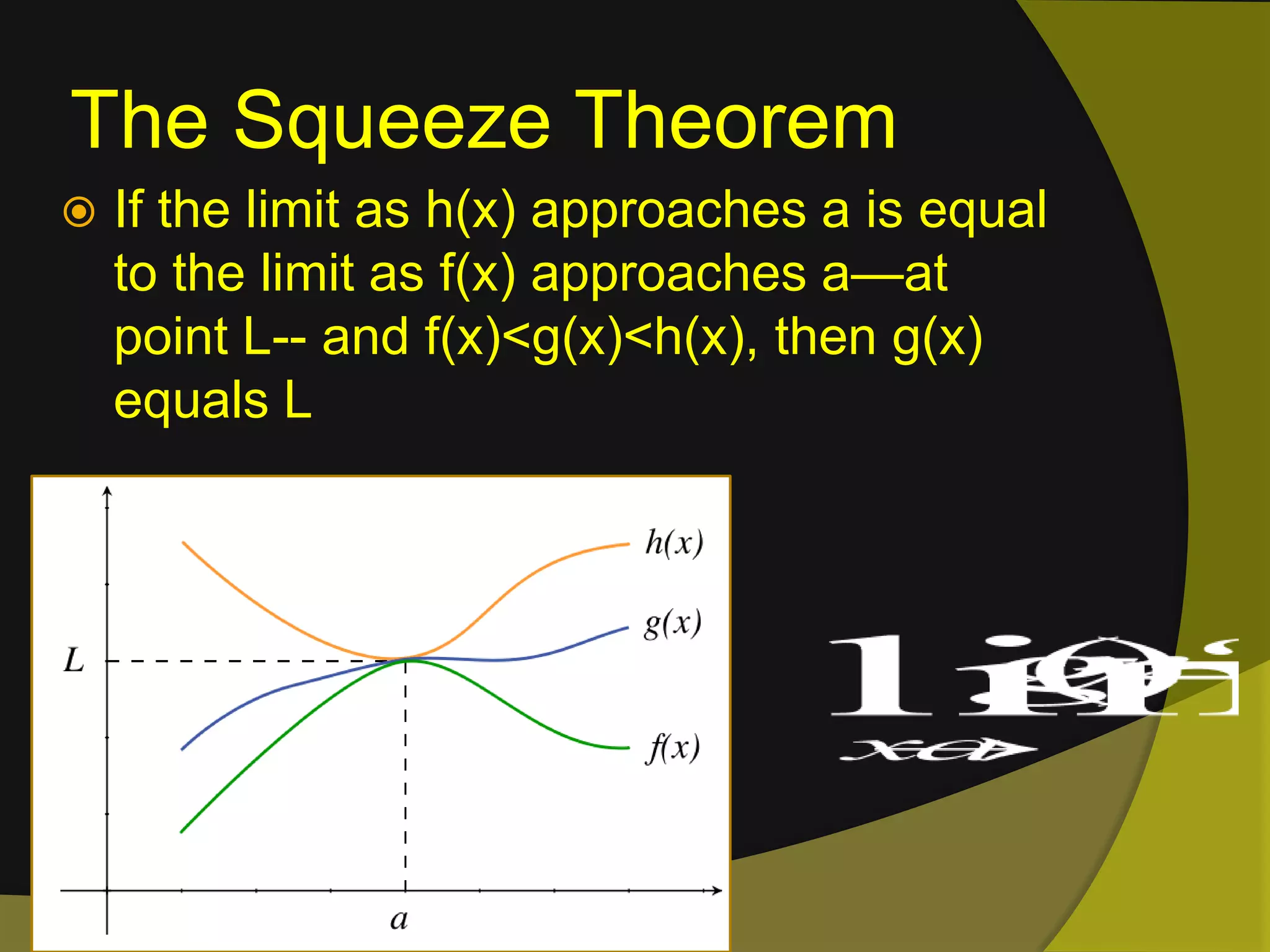
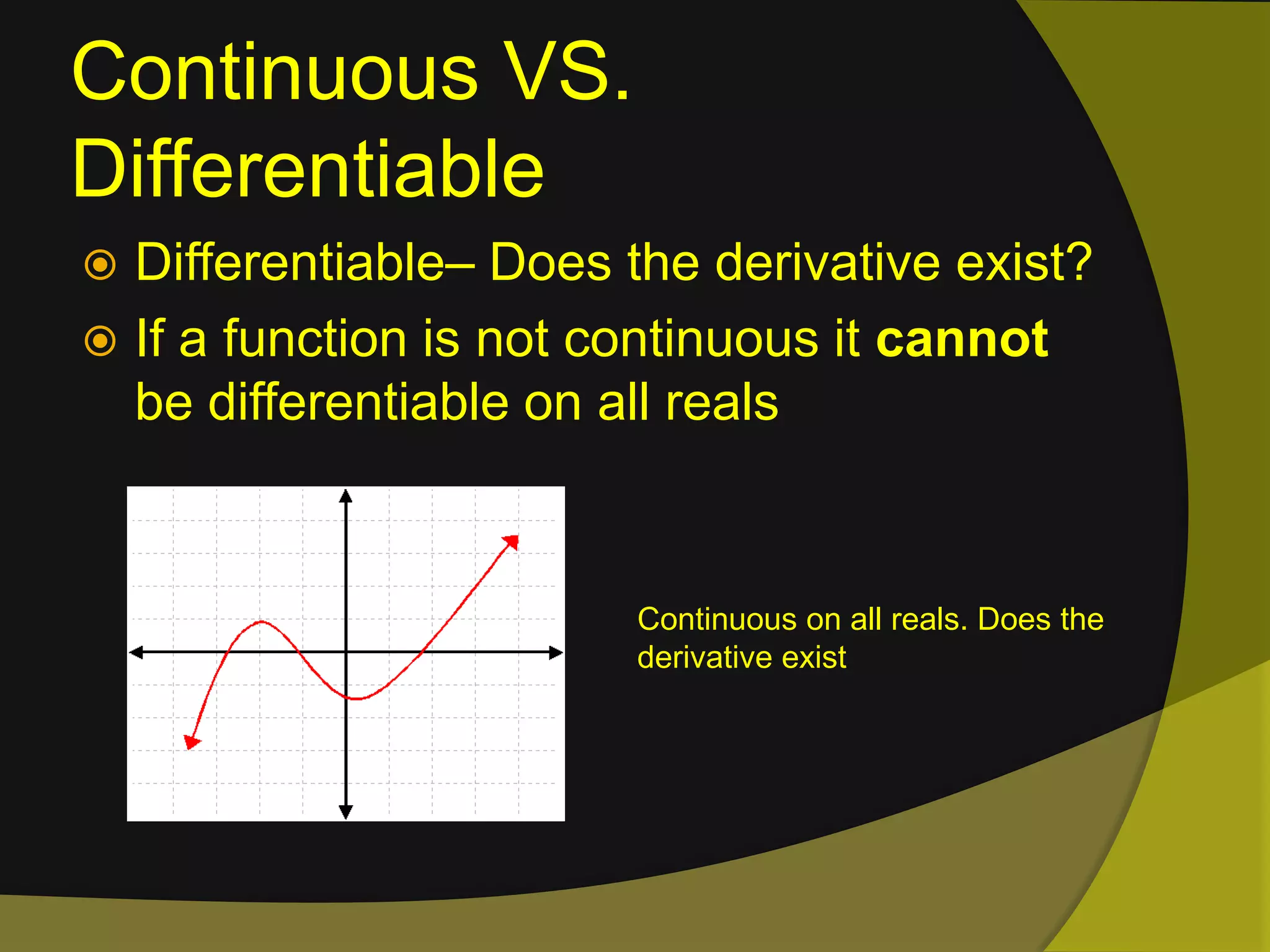
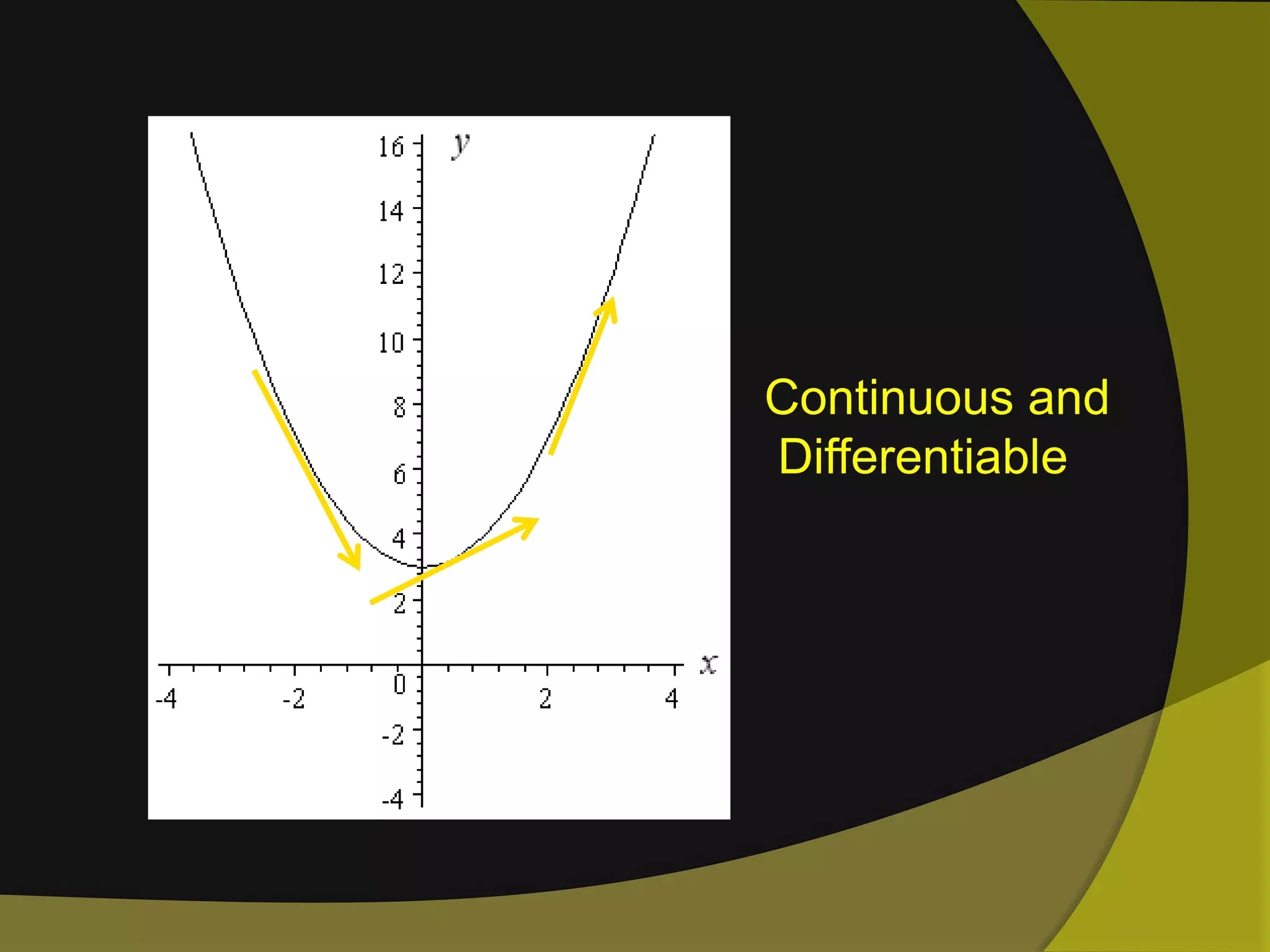
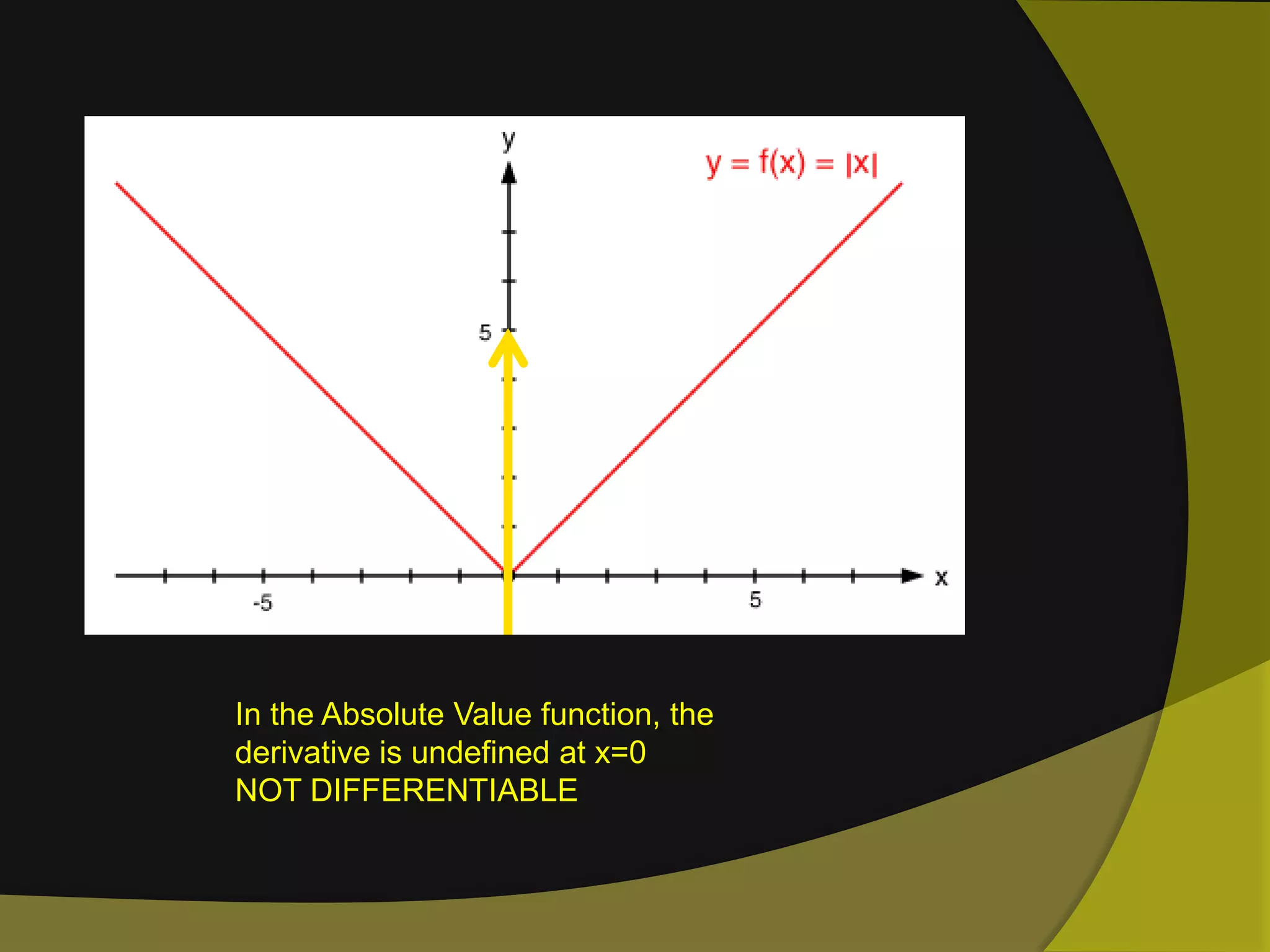
The document discusses limits and continuity in calculus. It defines a limit as the y-value of a graph as x approaches from both sides. It discusses different types of discontinuities such as jumps, holes, and asymptotes. It also discusses left-hand and right-hand limits, L'Hopital's Rule, the Squeeze Theorem, and the differences between continuous and differentiable functions. The Intermediate Value Theorem is also summarized as stating that if a function is continuous over an interval, there must exist a value within the interval.

1. Unit 1: LimitsHelga Hufflepuff

2. A limit is

3. A limit is the y-value of a graph as x approaches from both sides

6. A limit does not exist when the y-value is different as you approach the same x value from different sides

7. If the function is continuous…you can draw the function without ever having to pick up your pen from the graphThe limit value is the same as the function value

8. DiscontinuityTypes of Discontinuity:Jump HoleInfinite (Asymptote)

9. Left- and Right-Hand LimitsSometimes, limits do not approach the same y-value as they approach the same x-value, but the limit still existsIf approaching from the left -If approaching from the right +

10. L’Hopital’s RuleUsed to calculate limits involving indeterminate forms; 0/0 or ∞/∞Is there a limit?

11. 1) Let’s find the derivative of y/x:2) Since x’=1, we can now find the limit. The limit is 1

12. The Squeeze TheoremIf the limit as h(x) approaches a is equal to the limit as f(x) approaches a—at point L-- and f(x)<g(x)<h(x), then g(x) equals L

13. Continuous VS. DifferentiableDifferentiable– Does the derivative exist?If a function is not continuous it cannot be differentiable on all realsContinuous on all reals. Does the derivative exist

14. Differentiable?If the function is continuous, we only need to worry about where derivative is undefinedCusps CornersAt x=2, the derivative is undefinedThe function is differentiable on all reals except for where x=2

15. Continuous and Differentiable

16. In the Absolute Value function, the derivative is undefined at x=0NOT DIFFERENTIABLE

17. Intermediate Value TheoremIf the function is continuous from [a,b], then there must be a point c in the interval [a,b] and it must have a y-value that is between f(a) and f(b)