More Related Content
PDF
PPTX
PDF
状態空間モデルの考え方・使い方 - TokyoR #38 PPTX
Sliced Wasserstein距離と生成モデル PPTX
PDF
PDF
基礎からのベイズ統計学 輪読会資料 第4章 メトロポリス・ヘイスティングス法 PPTX
What's hot
PPTX
PDF
PDF
PDF
PDF
[DL輪読会]Recent Advances in Autoencoder-Based Representation Learning PDF
PDF
MCMCサンプルの使い方 ~見る・決める・探す・発生させる~ PDF
PPTX
PDF
実践多クラス分類 Kaggle Ottoから学んだこと PPTX
マルコフ連鎖モンテカルロ法 (2/3はベイズ推定の話) PPT
PDF
PDF
PDF
PDF
PDF
「内積が見えると統計学も見える」第5回 プログラマのための数学勉強会 発表資料 PPTX
[DL輪読会]Learning convolutional neural networks for graphs PDF
PDF
Similar to レプリカ交換モンテカルロ法で乱数の生成
PDF
RBM、Deep Learningと学習(全脳アーキテクチャ若手の会 第3回DL勉強会発表資料) PDF
渡辺澄夫著「ベイズ統計の理論と方法」5.1 マルコフ連鎖モンテカルロ法 PPTX
PDF
PDF
RStanとShinyStanによるベイズ統計モデリング入門 PPTX
PDF
MLaPP 24章 「マルコフ連鎖モンテカルロ法 (MCMC) による推論」 PDF
PDF
MCMCとともだちになろう【※Docswellにも同じものを上げています】 PDF
PDF
PDF
ベイズ推定でパラメータリスクを捉える&優れたサンプラーとしてのMCMC PDF
クラシックな機械学習の入門 10. マルコフ連鎖モンテカルロ 法 PDF
PDF
PDF
PDF
Infomation geometry(overview) PDF
PDF
PRML Chapter 11 (11.0-11.2) PDF
Monte Carlo Methods (Chapter 17 in Deep learning by Ian Goodfellow) More from Nagi Teramo
PDF
東京R非公式おじさんが教える本当に気持ちいいパッケージ作成法 PDF
PDF
PDF
続わかりやすいパターン認識11章(11.1 - 11.4) PDF
PDF
「plyrパッケージで君も前処理スタ☆」改め「plyrパッケージ徹底入門」 PDF
~knitr+pandocではじめる~『R MarkdownでReproducible Research』 PDF
PDF
healthplanetパッケージで�体組成データを手に入れて�健康な体も手に入れる PDF
Tokyo.R 白熱教室「これからのRcppの話をしよう」 PDF
PDF
PPTX
Reproducebility 100倍 Dockerマン PDF
PDF
Trading volume mapping R in recent environment PDF
可視化周辺の進化がヤヴァイ~rChartsを中心として~ PDF
PDF
PDF
PDF
レプリカ交換モンテカルロ法で乱数の生成
- 1.
第5回Tokyo. ciPy
レプリカ交換モンテカルロ法
で乱数の生成
@teramonagi
- 2.
目次
1. 自己紹介
2. モチベーション
3. マルコフ連鎖モンテカルロ法
4. レプリカ交換モンテカルロ法
5. まとめ
2
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
マルコフ連鎖モンテカルロ法
• 略して
–MCMC(Markov Chain MonteCarlo)
• 指定した確率(密度)関数に従う乱
数をマルコフ連鎖を活用することで
生成するモンテカルロ法のこと
• かなり汎用的な枠組み
9
- 10.
- 11.
- 12.
- 13.
- 14.
MCMC(メトロポリス法)
1. #適当なサイズだけ回す
2. SIZE = 10000
3. #初期状態を生成
4. x = [initial()] * SIZE
5. for i in range(1,SIZE):
6. #①:現在の状態から次の状態(候補)を選定
7. x_proposed = propose_next(x[i])
8. #②:確率密度の比を計算,target=密度関数
9. ratio = target(x_proposed) / target(x[i])
10. #③:一様乱数と比較し、遷移 or 元の状態のままを決定
11. if(np.random.uniform(size=1) < ratio):
12. x[i] = x_proposed
13. else:
14. x[i] = x[i-1]
Code:メトロポリス法実装例 in python
14
- 15.
- 16.
- 17.
- 18.
実際のコード(一部)
1. #正規分布の平均値
2. MU = 3.0
3. #シミュレーション・サイズ
4. SIZE_SIMULATION = 10000
5. X0 = np.array([0,0])
6. #次候補の選定関数
7. propose_next = lambda x:x+0.5*np.random.normal(size=len(x))
8. #target関数&MCMCオブジェクト生成
9. target = generate_target(MU)
10. mcmc = pyremc.MCMC(X0, target, propose_next, 10)
11. #MCMC実行
12. x = X0
13. for i in range(SIZE_SIMULATION):
14. x = np.vstack((x, mcmc.next()))
15. plot_result(x, MU)
Code:シミュレーションコード一部抜粋 in python
18
- 19.
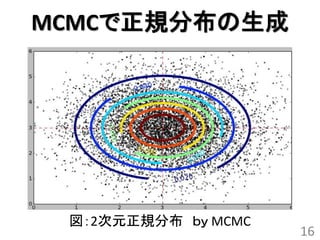
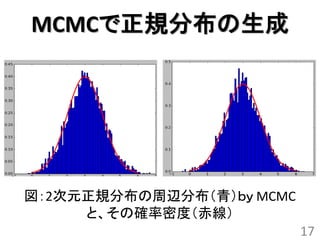
MCMCで正規分布生成
• 結果(概要)
–X方向:平均:3.05,標準偏差:1.03
–Y方向:平均:3.00,標準偏差:1.03
• うまくいっているように思える
• これはいい方法ダゾ!!!
19
- 20.
- 21.
- 22.
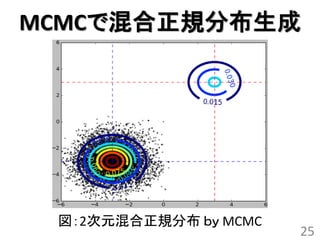
MCMCで混合正規分布生成
• 2次元の混合正規分布を生成
–混合数:2
–パラメータ
1 0
1 , 1 , w1 2,2,
,0.3
0 1
1 0
2 , 2 , w2 2,2,
,0.7
0 1
• メトロポリス法を10,000回試行
22
- 23.
- 24.
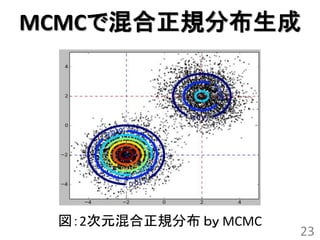
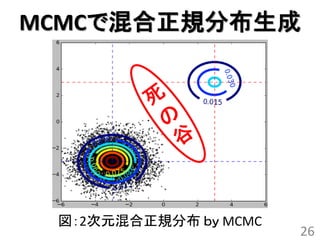
MCMCで混合正規分布生成
• 2次元の混合正規分布を生成
–混合数:2
–パラメータ
1 0
1 , 1 , w1 3,3,
,0.3
0 1
1 0
2 , 2 , w2 3,3,
,0.7
0 1
• メトロポリス法を10,000回試行
24
- 25.
- 26.
- 27.
- 28.
- 29.
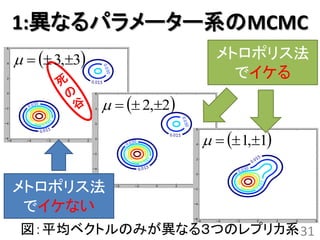
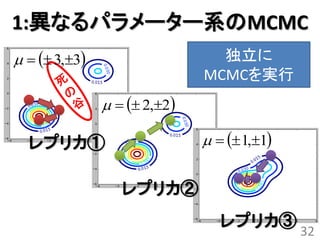
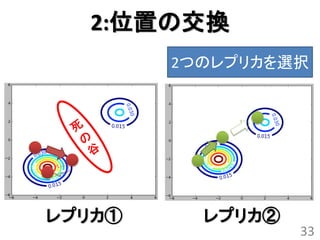
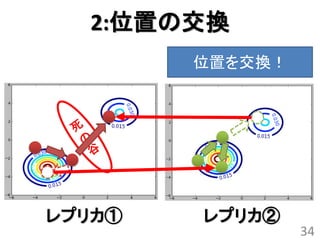
レプリカ交換モンテカルロ法
• 異なるパラメータを持つ確率分布(レプリカ)
を考えてそれらを交換するモンテカルロ法
–Replica Exchange MonteCarlo(REMC)
• 別名:パラレル・テンパリング法
• 元々はスピングラスのシミュレーション手法
– Hukushima-Nemoto, (1996), Multiple coupled Markov
chain MC , Parallel tempering
– Swendsen RH and Wang JS (1986) Replica Monte Carlo
simulation of spin glasses Physical Review Letters 57
29
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
REMCのコード
1. self._counter+=1
2. #①:全てのレプリカをMCMCで回す
3. for index_replica in range(self._replica_size):
4. self._mcmcs[index_replica].next()
5. #②:適当な交換頻度で位置の交換
6. if(self._counter % self._exchange_frequency == 0):
7. index_exchange = int(np.random.uniform(0,
self._replica_size-1))
8. x1 = self._mcmcs[index_exchange ].x
9. x2 = self._mcmcs[index_exchange+1].x
10. target1 = self._mcmcs[index_exchange ]._target
11. target2 = self._mcmcs[index_exchange+1]._target
12. #③:位置の交換はメトロポリス法に従う形で実行
13. if(np.random.uniform(size=1) <
(target1(x2)*target2(x1))/(target1(x1)*target2(x2))):
14. self._mcmcs[index_exchange].x,
self._mcmcs[index_exchange+1].x = np.copy(x2),np.copy(x1)
Code:REMC実装例(一部抜粋) in python 35
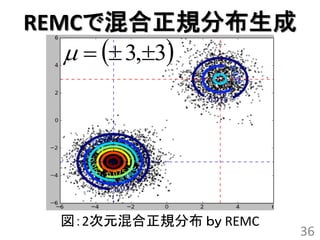
- 36.
- 37.
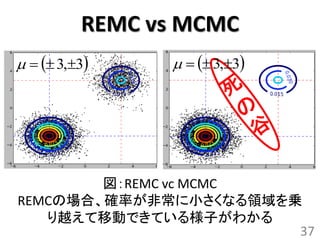
REMC vs MCMC
3,3 3,3
図:REMC vc MCMC
REMCの場合、確率が非常に小さくなる領域を乗
り越えて移動できている様子がわかる
37
- 38.
- 39.
- 40.
- 41.











![MCMC(メトロポリス法)
1. #適当なサイズだけ回す
2. SIZE = 10000
3. #初期状態を生成
4. x = [initial()] * SIZE
5. for i in range(1,SIZE):
6. #①:現在の状態から次の状態(候補)を選定
7. x_proposed = propose_next(x[i])
8. #②:確率密度の比を計算,target=密度関数
9. ratio = target(x_proposed) / target(x[i])
10. #③:一様乱数と比較し、遷移 or 元の状態のままを決定
11. if(np.random.uniform(size=1) < ratio):
12. x[i] = x_proposed
13. else:
14. x[i] = x[i-1]
Code:メトロポリス法実装例 in python
14](https://image.slidesharecdn.com/tokyoscipy520130126-130125162547-phpapp02/85/slide-14-320.jpg)

![実際のコード(一部)
1. #正規分布の平均値
2. MU = 3.0
3. #シミュレーション・サイズ
4. SIZE_SIMULATION = 10000
5. X0 = np.array([0,0])
6. #次候補の選定関数
7. propose_next = lambda x:x+0.5*np.random.normal(size=len(x))
8. #target関数&MCMCオブジェクト生成
9. target = generate_target(MU)
10. mcmc = pyremc.MCMC(X0, target, propose_next, 10)
11. #MCMC実行
12. x = X0
13. for i in range(SIZE_SIMULATION):
14. x = np.vstack((x, mcmc.next()))
15. plot_result(x, MU)
Code:シミュレーションコード一部抜粋 in python
18](https://image.slidesharecdn.com/tokyoscipy520130126-130125162547-phpapp02/85/slide-18-320.jpg)

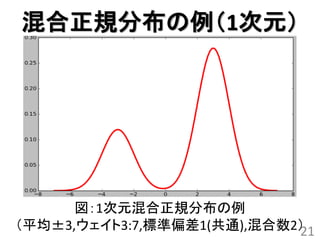
![混合正規分布
• 正規分布の重ね合わせで表現され
る分布 N
• 密度関数: px wi N x | i
i 1
• パラメータ
N : 正規分布の混合数
wi : 混合ウェイト([0,1])
20](https://image.slidesharecdn.com/tokyoscipy520130126-130125162547-phpapp02/85/slide-20-320.jpg)






![REMCのコード
1. self._counter+=1
2. #①:全てのレプリカをMCMCで回す
3. for index_replica in range(self._replica_size):
4. self._mcmcs[index_replica].next()
5. #②:適当な交換頻度で位置の交換
6. if(self._counter % self._exchange_frequency == 0):
7. index_exchange = int(np.random.uniform(0,
self._replica_size-1))
8. x1 = self._mcmcs[index_exchange ].x
9. x2 = self._mcmcs[index_exchange+1].x
10. target1 = self._mcmcs[index_exchange ]._target
11. target2 = self._mcmcs[index_exchange+1]._target
12. #③:位置の交換はメトロポリス法に従う形で実行
13. if(np.random.uniform(size=1) <
(target1(x2)*target2(x1))/(target1(x1)*target2(x2))):
14. self._mcmcs[index_exchange].x,
self._mcmcs[index_exchange+1].x = np.copy(x2),np.copy(x1)
Code:REMC実装例(一部抜粋) in python 35](https://image.slidesharecdn.com/tokyoscipy520130126-130125162547-phpapp02/85/slide-35-320.jpg)