研究室内PRML勉強会 11章2-4節

研究室内PRML勉強会 11章2-4節

• 1.
  PRML 読書会 11.2-11.4 2011.07.1919:30- M2 松田耕史
• 2.
  マルコフ連鎖モンテカルロとは •  複雑な分布から「マルコフ連鎖」をもちいてサンプリングする手 法の総称 •  「マルコフ連鎖」する提案分布を用いる •  Gibbs Samplingは素直な解釈では提案分布を用いないが、提案分布をもつ 形にも書ける(後述) •  「マルコフ連鎖」する：サンプリングを行うごとに状態がかわる •  状態がかわる：という性質 •  単純に棄却を行うより、広い範囲を効率よくサンプルすることができる •  特に高次元の問題で重要 •  状態に良し悪しの尺度(尤度等)をつけることで、最適化の手法としても 用いることができる(おまけ) •  記号の概略 •  確率変数の状態 : z , 提案分布 : q , サンプリングを行いたい分布 : p
• 3.
  11.2 マルコフ連鎖モンテカルロ •  マルコフ連鎖を成す提案分布からのサンプリング (! ) •  提案分布は、現在の状態に依存する q(z | z ) •  簡単な例 ) Metropolisアルゴリズム 1.  提案分布 q( z | z(t) ) から z* をサンプリングする 2.  A (z*, z(t)) = min{1, p(z*)/p(z(t))}      (11.33) 3.  (0,1)の一様分布から u をサンプルして •  A (z*, z(t)) > u の場合 z(t+1) = z* •  otherwise z(t+1) = z(t) 4.  ステップ1に戻る •  つまり、 提案分布qからサンプルをもってきて •  p(z) が増加するなら z* を「必ず」採択 •  p(z) が減少する場合も 減少率に反比例した確率 で z* を採択
• 4.
  Metropolisアルゴリズムの注意点 •  サンプリングを十分繰り返すと、z(t)の分布はp(z)からのサンプ ルに近づく •  ただし、連続したサンプルは高い相関を持っている •  (同じ値である場合もある) •  p(z)からの独立したサンプルを得たい場合は、得られたサン プルから間引きをする必要がある •  提案分布について •  分散が大きい(ステップ数が大きい) •  棄却される可能性が高くなり、効率的な  サンプリングが行えない •  分散が小さい(ステップ数が小さい) •  z同士の相関が消えにくい
• 5.
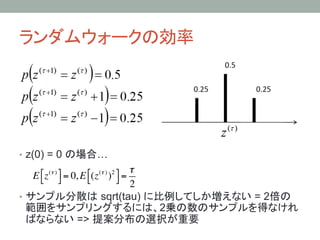
  ランダムウォークの効率 •  z(0) =0 の場合… ! E ! z (! ) # = 0, E !(z (! ) )2 # = " $ " $ 2 •  サンプル分散は sqrt(tau) に比例してしか増えない = 2倍の 範囲をサンプリングするには、2乗の数のサンプルを得なけれ ばならない => 提案分布の選択が重要
• 6.
  マルコフ連鎖の定義と性質 (1/2) •  (一次の)マルコフ連鎖とは (11.37) •  遷移確率 •  均一マルコフ連鎖とは •  分布が不変である、定常である、とは (11.39) どのステップにおいても、状態z’からzへの遷移は同じ確率
• 7.
  マルコフ連鎖の定義と性質 (2/2) •  詳細釣り合い条件 •  いかなる状態zに対しても、逆変換が同じ分布になる •  エルゴード性 •  どんな初期状態z(0)からスタートしても、サンプリングを沢山くりかえすこ とでサンプルzの分布はp*(z)に収束する •  p(z)がゼロでない領域であれば、「どこからでも」「どこへでも」ゼロでは ない確率で遷移できるということ •  MCMC全般において、非常に重要
• 8.
  Metropolis-Hastings Algorithm •  Metropolisアルゴリズムとほとんど同じ。対象でない提案分布 を扱えるようにしてある •  等方ガウス分布は対称、しかし、そうでないガウス分布は対称ではない 1.  提案分布 q から z* をサンプル 2.  次の確率でサンプルを採択、棄却 (11.44) •  対称な提案分布については、 Metropolisアルゴリズムと等価
• 9.
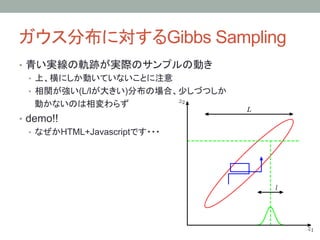
  11.3 Gibbs Sampling • 例）三変数の場合を考える 1.  まずそれぞれの確率変数ziを適当に初期化 2.  各ステップtauにおいて以下のようにサンプルする 1.  2.  3.    (11.46-11.48) •  一般的な形については p.258 参照 •  サンプリングする順番は適当に決めて良い（順番にでも、ランダムにでも) •  MHアルゴリズムと同様、初期値から相関が消えるにはそれなりに 時間がかかる(隣接するサンプル同士も相関を持っている) •  条件付き分布のエルゴード性が重要 •  確率変数の空間の中で「どこからでも」「どこへでも」行けなければならない
• 10.
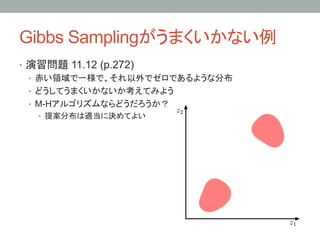
  Gibbs Sampling とM-H Algorithm •  Gibbs Samplingは Metropolis-Hasting Algorithmの特別な 場合とみなすことができる •  M-H法における提案分布をGibbs Samplingにおける条件付き分布とみ なすと、二つのアルゴリズムは等価になる •  11.49 式参照 •  この場合、採択率は1になるということに注意
• 11.
  ガウス分布に対するGibbs Sampling •  青い実線の軌跡が実際のサンプルの動き •  上、横にしか動いていないことに注意 •  相関が強い(L/lが大きい)分布の場合、少しづつしか  動かないのは相変わらず •  demo!! •  なぜかHTML+Javascriptです・・・
• 12.
  Gibbs Samplingがうまくいかない例 •  演習問題11.12 (p.272) •  赤い領域で一様で、それ以外でゼロであるような分布 •  どうしてうまくいかないか考えてみよう •  M-Hアルゴリズムならどうだろうか？ •  提案分布は適当に決めてよい
• 13.
  グラフィカルモデルとGibbs Sampling •  マルコフブランケットの議論(8章)を思い出してみよう •  無向グラフの場合、p(z)はマルコフブランケットの塗りつぶされたノード にのみ依存する •  近傍ノードを固定して、中央のノードをサンプル •  別のノードを選択して、中央のノードをサンプル •  という手続きを繰り返すことによって、全体がいい感じになるようなzを求 めることができそう(ICMアルゴリズムとの関連性 -> 8.3.3) •  過剰緩和、対数凹とか関数形のお話は省略します
• 14.
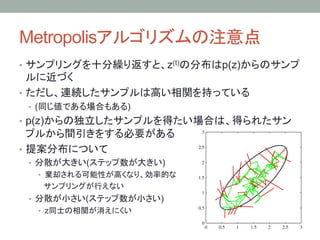
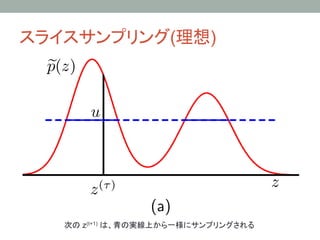
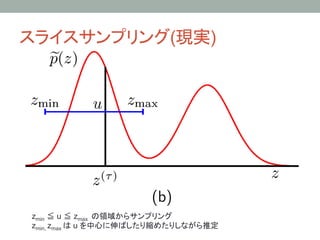
  11.4 スライスサンプリング •  Metropolisアルゴリズムはステップサイズ(提案分布の分散) に敏感 •  小さすぎ : ランダムウォーク的に振る舞い、相関が消えにくい •  大きすぎ : 棄却されることが多くなる •  u という補助的な変数を導入することでサンプリング範囲を適 応的に決める 1.  zの初期値を適当に定めたら,以下の2ステップを交互に 1.  Sample u ~ Uniform(0,p(z)) •  縦にサンプリング(スライスする場所(高さ)を決める) 2.  Sample z ~ Uniform({ z : p(z) < u }) •  横にサンプリング (スライスされた平面(領域)から一様にサンプル)
• 15.
  スライスサンプリング(理想) 次の z(t+1) は、青の実線上から一様にサンプリングされる
• 16.
  スライスサンプリング(現実) zmin ≦ u≦ zmax の領域からサンプリング zmin, zmax は u を中心に伸ばしたり縮めたりしながら推定
• 17.
  まとめ •  マルコフ連鎖モンテカルロ •  マルコフ連鎖をもちいて、分布からサンプルを得る手法の総称 •  提案分布を用いるアルゴリズム(マルコフ的棄却法) •  Metropolis アルゴリズム : 提案分布が対称 •  Metropolis-Hasting アルゴリズム : 非対称な提案分布を扱える •  提案分布の設計が重要 •  条件付き分布を用いるアルゴリズム •  Gibbs Sampling •  M-H法において提案分布 = 条件付き分布と置いたものと等価 •  棄却されないので、条件付き分布からのサンプルが容易であれば高効率 •  補助変数を導入するアルゴリズム •  スライスサンプリング •  “スライス点”を一様にサンプル & “スライスされた領域”から一様に(スライス点を)サンプル •  Gibbs Samplingと似ているが、スライス領域の計算が面倒(な場合がある) •  各手法、一長一短があるので、使い分けられると良いですね •  NLPではGibbs Samplingをみかけることが多いが、その他の方法も知っておこう
• 18.
  何のためにサンプリングを行うか •  あくまで私の認識ですが・・・ •  期待値計算 •  （複雑な）事後分布のサンプルを得ることで、期待値、中央値等の近似 値を求める •  EM における E-stepの代替 (ex. IPアルゴリズム) •  LDA等におけるGibbs Samplingはこちら •  ある単語があるトピックに紐づく確率の期待値を求める •  最適化 •  たとえば尤度関数は分かっているが、最尤推定ができないという状況で、 尤度関数が最大になる点(できれば大域解)を求める •  Simulated-Annealing と M-Hアルゴリズム の類似性 •  Simulated-Annealingと同様、M-Hアルゴリズムも多峰性をもつ場合もまぁ まぁ動く
• 19.
  補遺 •  Sequential MonteCarlo(SMC)アルゴリズム •  MCMCと似ているが、各ステップで”沢山”サンプルする •  そして、それらのサンプルをもちいて •  モデルパラメータを調節したり、期待値を求めたり •  パーティクルフィルタ •  時系列モデルにおいて、（かくれ）状態が変化する点を求める問題 •  M-H法とSimulated Annealingにおける（考え方の)類似性が、 SMCとGA(遺伝的アルゴリズム)においてもみられる •  GAについては、適応システム論あたりの講義でやったかな？ •  ただし、「期待値計算」の世界と「最適化」の世界を区別するこ とは重要らしい
• 20.
  統計科学のフロンティア12 p.72より