Download as PDF, PPTX
![(34)
はじめに
• 本資料は、[1]‐[4]の自分なりの理解メモです
– [1]‐[2]は、マーク付き点過程の直観的な理解、[3]‐[4]はマーク付き点過程とノンパラベイズとの関係
の理解を得るにあたって、大変参考になりました
• [1] Bognar, Matthew A. "Bayesian modeling of continuously marked spatial point patterns." Computational
Statistics 23.3 (2008): 361‐379.
• [2] Ortner, Mathias, Xavier Descombes, and Josiane Zerubia. "Building extraction from digital elevation
models.“, http://hal.archives‐ouvertes.fr/docs/00/07/20/71/PDF/RR‐4517.pdf
• [3] 佐藤一誠, “基礎からのBayesian Nonparametrics.” http://www.slideshare.net/issei_sato/bayesian‐
nonparametrics
• [4] 佐藤一誠, “Bayesian Nonparametrics入門 .“ http://www.slideshare.net/issei_sato/ppml
2](https://image.slidesharecdn.com/random-140604001854-phpapp01/85/slide-2-320.jpg)
![(34)
アプリ例
• 人のカウンティング
– 点：重心、マーク：輪郭
点
マーク
人のカウンティング
Marked point processes for crowd counting[CVPR09]
4](https://image.slidesharecdn.com/random-140604001854-phpapp01/85/slide-4-320.jpg)
![[DL輪読会]Deep Learning 第15章 表現学習](https://cdn.slidesharecdn.com/ss_thumbnails/deeplearning15-180601023904-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DL輪読会]NVAE: A Deep Hierarchical Variational Autoencoder](https://cdn.slidesharecdn.com/ss_thumbnails/nvaeadeephierarchicalvariationalautoencoder-201113004930-thumbnail.jpg?width=640&height=640&fit=bounds)
![集中不等式のすすめ [集中不等式本読み会#1]](https://cdn.slidesharecdn.com/ss_thumbnails/concentrationintro-150128034517-conversion-gate02-thumbnail.jpg?width=640&height=640&fit=bounds)
マーク付き点過程
- 1.
- 2. (34) はじめに • 本資料は、[1]‐[4]の自分なりの理解メモです – [1]‐[2]は、マーク付き点過程の直観的な理解、[3]‐[4]はマーク付き点過程とノンパラベイズとの関係 の理解を得るにあたって、大変参考になりました •[1] Bognar, Matthew A. "Bayesian modeling of continuously marked spatial point patterns." Computational Statistics 23.3 (2008): 361‐379. • [2] Ortner, Mathias, Xavier Descombes, and Josiane Zerubia. "Building extraction from digital elevation models.“, http://hal.archives‐ouvertes.fr/docs/00/07/20/71/PDF/RR‐4517.pdf • [3] 佐藤一誠, “基礎からのBayesian Nonparametrics.” http://www.slideshare.net/issei_sato/bayesian‐ nonparametrics • [4] 佐藤一誠, “Bayesian Nonparametrics入門 .“ http://www.slideshare.net/issei_sato/ppml 2
- 3.
- 4.
- 5. (34) （マーク付き）点過程の特徴 • 特徴 – 無限次元の離散点を扱う事が出来る •連続関数（時間、空間）を任意法則に従って離散化 • 特徴を生かした応用 – ノンパラベイズの構成 • 事前分布（パラメータ空間）の無限次元離散化によるモデル数推定 – ※今回紹介しませんが、離散化をキーワードに考えると、他にも色々ありそうです 5
- 6. (34) アウトライン • モデル化 – 確率的に点とマークを打つということ –確率密度関数 • 応用（他分野への横展） – ノンパラベイズ • パラメータ推定 – 目的関数 – MCMCの設計 • まとめ 6
- 7. (34) アウトライン • モデル化 – 確率的に点とマークを打つということ –確率密度関数 • 応用（他分野への横展） – ノンパラベイズ • パラメータ推定 – 目的関数 – MCMCの設計 • まとめ 7
- 8. (34) 強度 β X amaxamin 確率的に点とマークを打つということ（1/3） • 強度関数= 強度×基底測度 – 強度: 単位時間あたりの点の数の期待値（大域的な点の密度） – 基底測度 : 時間軸の長さ（局所的な点の密度） X λ(A)=β×μ(A) μ(A)=|amax‐amin| λ(A) 強度関数 基底測度 β強度 μ(A) 点 8
- 9. (34) 確率的に点とマークを打つということ（2/3） • 強度関数= 強度×基底測度 – 強度: 単位時間あたりの点の数の期待値（大域的な点の密度） – 基底測度 : 時間軸の長さ（局所的な点の密度） X λ(A)=β×G0(A) G0(A) 強度関数 基底測度 β強度 ex. Gauss G0(A) X 基底測度 強度 β X 点 9
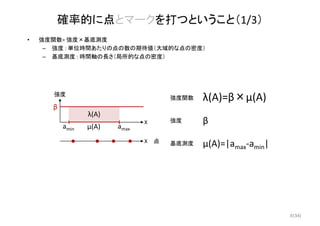
- 10. (34) 確率的に点とマークを打つということ（3/3） • 強度関数= 強度×基底測度 ×マーク分布 – 強度 : 単位時間あたりの点の数の期待値（大域的な点の密度） – 基底測度 : 時間軸の長さ、マーク分布 : マークの従う分布（局所的な点の密度） • マークも点の次元と考える、ただし点の数は規定しない X λ(A,B)=βG0(A)×ν(B) G0(A) 強度関数 基底測度 β強度 ex. Gauss G0(A) X 基底測度 強度 β X 点 ν(B) マーク M ν(B) ex. Gauss 10
- 11. (34) 確率密度関数（1/3） • 累積分布関数を、点とマークの打ち方のパターン で微分 –我々が良く知る確率密度関数のdx（目盛り）が、確率的に打たれるイメージ – 確率にするため、目盛上に長さ1の棒をたてた後に正規化 • , は無限次元であることに注意 – は , の値と次数を含めた分配関数 , ℙ , 1 ∈ ∈ ∈ ∈ , βG0 ν X M 11
- 12.
- 13. (34) 確率密度関数（3/3） • 基底測度とマーク分布を一様にできる – 基底測度とマーク分布の形状を、重み, に押し付ける , ℙ , 1 , , , βμ u X M , | | : Uniform 基底測度・マーク分布の押し付け 13
- 14. (34) 2つの疑問 • 基底測度とマーク分布の情報が結局 ,に入ってるけど、点を打つプロセスとか意味あるの？ – あります – 時系列・空間上の点 , は無限次元 – 次数が異なる , を扱うため、何らかの形でその次数を表現する上位モデルが必要 – この上位モデルが , – 値的には、 , の分配関数 , , に埋め込まれている • , に押し付けると、何が嬉しいの？ – モデルの構成が単純になる • 少しひねっただけで、強度関数をまともにかけなくなる – 最適化（MCMC）の構成が超簡単になる 14
- 15. (34) の代表的な決め方 • ギブス分布を採用し、引数となるエネルギー関数に、表現したいモデルを突っ込む , ℙ , 1 exp , exp, , , : 任意のエネルギー関数 15
- 16. (34) アウトライン • モデル化 – 確率的に点とマークを打つということ –確率密度関数 • 応用（他分野への横展） – ノンパラベイズ • パラメータ推定 – 目的関数 – MCMCの設計 • まとめ 16
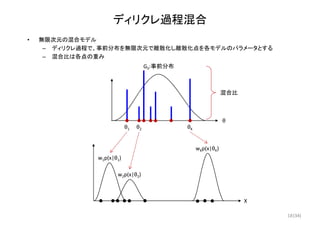
- 17. (34) ディリクレ過程 • 定義 – 可測空間Ω, の基底測度を 、集中度を とする – 確率測度 が ~ , に従うとき、任意のdisjointなΩの分割 , … , に対して – , … , ~Dirichlet , … , • 翻訳 – 基底測度 を に従う密度で離散化 – 各離散点には、正値で、総和が1となる重み（離散点を選ぶDirichlet分布のパラメータ） G0 G0を離散化した点（ G0に従う） 各点の重み（選択確率） ∗ :区間 ∗の重みの総和 17
- 18. (34) ディリクレ過程混合 • 無限次元の混合モデル – ディリクレ過程で、事前分布を無限次元で離散化し離散化点を各モデルのパラメータとする –混合比は各点の重み G0:事前分布 混合比 θ1 θ2 θK θ X w1p(x|θ1) w2p(x|θ2) wKp(x|θK) 18
- 19. (34) マーク付き点過程的ディリクレ過程 • 定義 – 点：基底測度を、強度 に従う点 – マーク：正値をとり、総和が1となるよう正規化 βG0 強度（集中度） × 基底測度 ν マーク 正値をとる分布 点 正規化 19
- 20. (34) マーク付き点過程的ディリクレ過程混合 • 分散既知，混合数未知の混合ガウスの例 , , , 1 exp, ; , ∑ ; , 1 平均の事前分布 ガウス分布 正値をとる分布 ガンマ分布 混合比 重みの正規化 パラメータ 点 点とマーク（+押し付け） パラメータが点、混合比がマークに従う混合モデル , ; ln ; 0, ln G ; , βG0 強度（集中度） × 事前分布 マーク 正値をとる 分布 x1 x2 xK w1p(y|x1) w2p(y|x2) wKp(y|xK) y モデル 20
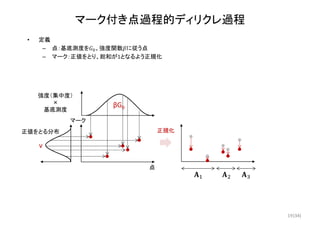
- 21. (34) パラメータ推定 • 目的関数 – 以下を満たす, を次数を含めて最適化 • ToyDataに対する最適化結果（MCMCを使う：後術の方法） ∗ , ∗ argmax , , , | , , :ハイパーパラメータ :モデルパラメータ :混合比（非正規化） 混合数 ―真値 ―推定値（xの次数） 混合比（正規化） パラメータ w1 w2 w3 x1 x2 x3 推定値 0.158 0.242 0.604 0.177 10.036 19.871 真値 0.186 0.208 0.606 0.976 10.027 19.883 21
- 22. (34) ノンパラベイズ構成まとめ • 混合モデルの混合数を分布としてもつ – 事前分布（パラメータ空間）から、可算無限個の離散点を抽出 –各点に重みをつける – 点：混合モデルのパラメータ、重み：混合比 • 点過程的に言うと • 事前分布（パラメータ空間）上にマーク付き点過程を構成 • 点：混合モデルのパラメータ、マーク：混合比 • 点とマークはエネルギー関数 , を適当に設計すれば、それっぽいものが出来る 22
- 23. (34) アウトライン • モデル化 – 確率的に点とマークを打つということ –確率密度関数 • 応用（他分野への横展） – ノンパラベイズ • パラメータ推定 – 目的関数 – MCMCの設計 • まとめ 23
- 24. (34) 目的関数と最適化の方針 • 目的関数 – 事前分布としてマーク付き点過程が存在する場合を想定 •最適化の方針 – MCMCを利用 • , , , | から、 所与のもと、 , をサンプリング • サンプル平均＝最適解 – 無情報事前分布を仮定したMAP推定 – アニーリングしてもよい – 注意点 • , をサンプリングする過程で、 , のサンプリングも必要 • , は無限次元 ∗, ∗ argmax , , , , | 尤度 事前分布：点過程 ※赤字・・・Unknown 24
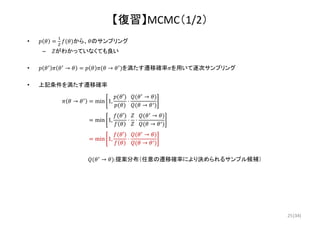
- 25. (34) 【復習】MCMC（1/2） • から、 のサンプリング –がわかっていなくても良い • → → を満たす遷移確率 を用いて逐次サンプリング • 上記条件を満たす遷移確率 → min 1, ′ ⋅ → → min 1, ′ ⋅ ⋅ → → min 1, ′ ⋅ → → → :提案分布（任意の遷移確率により決められるサンプル候補） 25
- 26. (34) 【復習】MCMC（2/2） • Given and ← 0 • Proposal Step – sampling from → • Acceptance‐Rejection Step – ← with probability – ← with probability 1 • min 1, ⋅ → → • ← 1 26
- 27. (34) マーク付き点過程のMCMC：遷移確率 • , ,, とすると、 , , , | からサンプルを得るための遷移確率 は、 → min 1, | , , ′ | , , ⋅ , | ′ , | → → min 1, | , , ′ | , , ⋅ exp , ; exp , ; ⋅ ⋅ → → Likelihood Ratio Prior Ratio Proposal Ratio Model Evidence Ratio 27
- 28. (34) マーク付き点過程のMCMC：アウトライン • Let ,, , , Given , , , , and ← 0 • Proposal Step – sampling from → • Acceptance‐Rejection Step – ← ∗ w.p. – ← w.p. 1 • ← 1 min 1, | , , ′ | , , ⋅ exp , ; exp , ; ⋅ ⋅ → → 28
- 29. (34) • Proposal Type – パラメータ値の摂動 •‐move , , , → , , , : w.p. • ‐move , , , → , , , : w.p. – 点の値の摂動 • ‐move , , , → , , , s. t. | | : w.p. • ‐move , , , → , , , s. t. | | : w.p. – 点の数の摂動 • , , , → , , ∪ , ∪ : w.p. • , , , → , , ∖ , ∖ : w.p. – where, ∑ ∗ 1, ∗ 0 29
- 30. (34) • , ,, ‐move – Symmetric • じゃなくてもいいけど、設計が楽なのでそうします – （例） ‐move , , , → , , , • → Uniform ∆ , Δ min 1, | , , ′ | , , ⋅ exp , ; exp , ; ⋅ ⋅ → → 30
- 31. (34) • , – Symmetricには出来ない •点を支配する確率（押し付け後のスッキリした奴）に従ってサンプリング – , – | | – : Uniform – , , , → , , ∪ , ∪ • , :点とマークの定義域とすると – , , , → , , ∖ , ∖ • :点 の数とすると → , , 1 ∵ : Uniform, | | → 1 ∵ | | 31
- 32. (34) • Importance Sampling – 説明は割愛（PRML下巻p.p.246‐248，p.p.270‐p.p.271） –ポイントは、 ⁄ の計算の為に（MCMCの各ステップで）別途サンプリングが必要 32
- 33. (34) というわけでマーク付き点過程のMCMC • Let ,, , , Given , , , , and ← 0 • Proposal Step – sampling from → • , , , ‐move : e.x. ‐move : Uniform ∆ , Δ • : ⁄ , : ⁄ • Acceptance‐Rejection Step – estimate ⁄ using Importance Sampling – ← ∗ w.p. , ← w.p. 1 • ← 1 min 1, | , , ′ | , , ⋅ exp , ; exp , ; ⋅, , , ‐move min 1, | , , ′ | , , ⋅ exp , ; exp , ; ⋅ ⋅ 1 min 1, | , , ′ | , , ⋅ exp , ; exp , ; ⋅ ⋅ 33
- 34. (34) まとめ • マーク付き点過程を紹介 – 連続関数（時間、空間）を任意法則に従って離散化 •重み , をうまく使うことで、複雑なモデルを表現可能 – ノンパラベイズ – ※ 離散化をキーワードに考えると他にも色々ありそうです • ただし、やりすぎると、最適化が大変なことに – サンプラーのネスト 34