Download as PDF, PPTX
![実装：
GPyOptでXgboostのハイパーパラメータ最適化
def blackbox(x):
learning_rate = float(x[:,0])
subsample = float(x[:,1])
colsample_bytree = float(x[:,2])
gamma = float(x[:,3])
reg_lambda = float(x[:,4])
max_depth = int(x[:,5])
n_estimators = int(x[:,6])
XGB_instance = xgb.XGBRegressor(learning_rate = learning_rate,
subsample = subsample,
colsample_bytree = colsample_bytree,
gamma = gamma,
reg_lambda = reg_lambda,
max_depth = max_depth,
n_estimators = n_estimators,
objective = "reg:linear")
scores = cross_val_score(XGB_instance,X_train,y_train,cv=4,scoring='mean_squared_errorʻ)
return -scores.mean()
xは1×nの⼆次元リス
トで渡されるので、各
パラメータを型変換
渡されたハイパーパ
ラメータでインスタ
ンス化
sklearnの
cross_val_scoreで
評価値を計算
・機械学習の⼀連の流れを関数として定義](https://image.slidesharecdn.com/bayseopt-200303133246/75/slide-23-2048.jpg)
![実装：
GPyOptでXgboostのハイパーパラメータ最適化
・探索してほしいハイパーパラメータの名前と値の範囲、連続or離散を以下のように定義
bounds = [{'name': 'learning_rate','type': 'continuous', 'domain': (0.0005,0.3)},
{'name': 'sub_sample','type': 'continuous', 'domain': (0.5,1)},
{'name': 'colsample_bytree','type': 'continuous', 'domain': (0.5,1)},
{'name': 'gamma','type': 'continuous', 'domain': (0,1)},
{'name': 'reg_lambda','type': 'continuous', 'domain': (0,1)},
{'name': 'max_depth','type': 'discrete', 'domain': tuple(list(range(3,8)))},
{'name': 'n_estimator','type': 'discrete', 'domain': tuple(list(range(30,210,10)))}]
continuous:連続 discrete：離散 （continuous→discreteの順でないとエラーになる）](https://image.slidesharecdn.com/bayseopt-200303133246/75/slide-24-2048.jpg)
![実装：
GPyOptでXgboostのハイパーパラメータ最適化
・最適化を⾏うクラスをインスタンス化し、run_optimizeメソッドで最適化を実⾏
initial_design_numdata：初期探索の回数
acquisition_type：獲得関数の設定
max_iter：最⼤探索回数
XGB_Bopt = GPyOpt.methods.BayesianOptimization(f=blackbox,
domain=bounds,
initial_design_numdata=5,
acquisition_type='LCB')
XGB_Bopt.run_optimization(max_iter=15)
・最適化終了後、x_opt,fx_opt メソッドで最適解、最適値を出⼒
print(XGB_Bopt.x_opt,XGB_Bopt.fx_opt)
→ array([ 0.20040502, 0.68832784, 0.66486351, 0.81031615, 0.66657359, 5, 140. ]),array([ 0.50715448])](https://image.slidesharecdn.com/bayseopt-200303133246/75/slide-25-2048.jpg)
![SSII2021 [OS2-01] 転移学習の基礎：異なるタスクの知識を利用するための機械学習の方法](https://cdn.slidesharecdn.com/ss_thumbnails/os2-02final-210610091211-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DL輪読会]相互情報量最大化による表現学習](https://cdn.slidesharecdn.com/ss_thumbnails/20190913iwasawa-190913002312-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DL輪読会]Deep Learning 第17章 モンテカルロ法](https://cdn.slidesharecdn.com/ss_thumbnails/deeplearning17-180601024803-thumbnail.jpg?width=640&height=640&fit=bounds)
ベイズ最適化
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
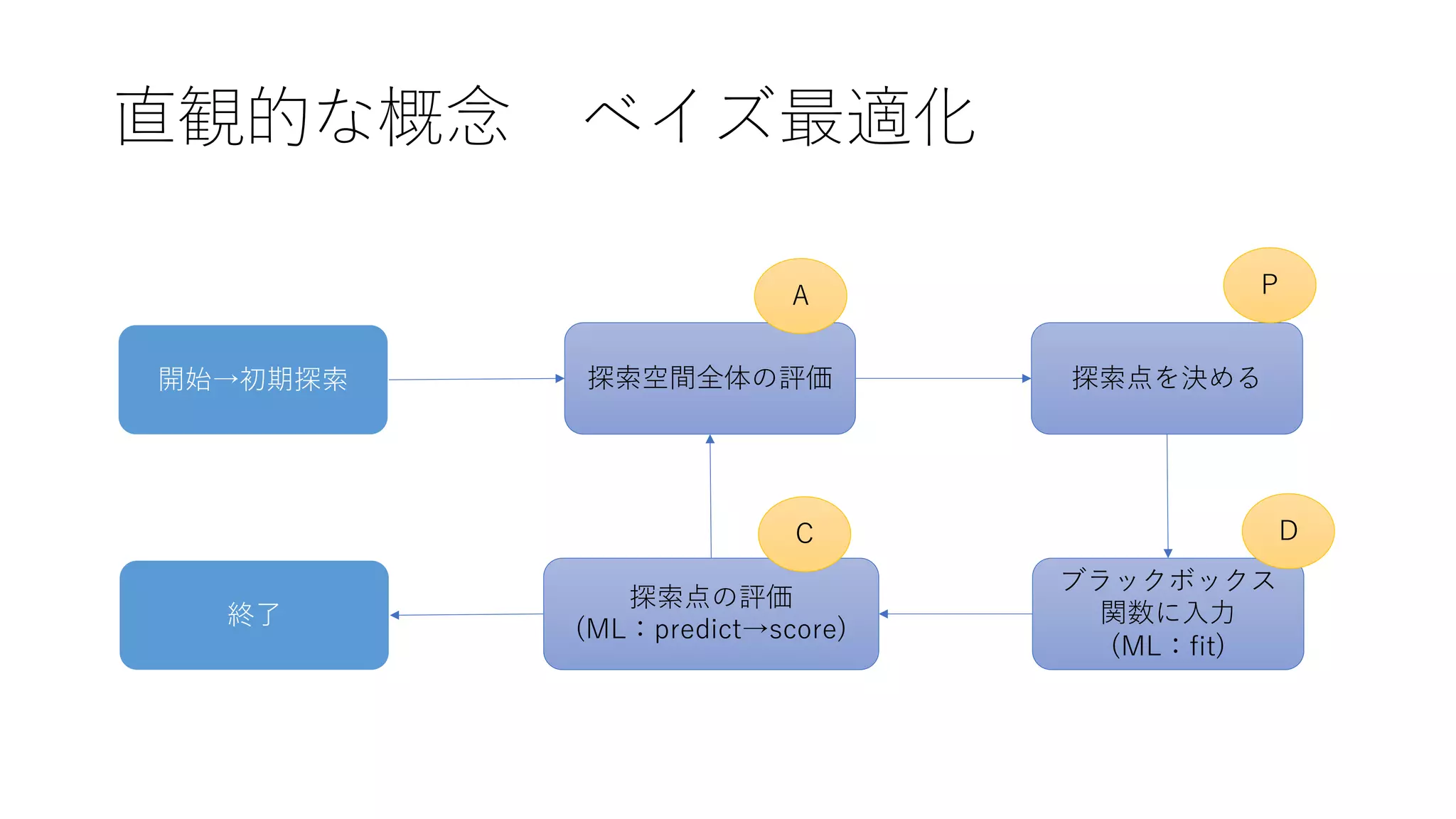
- 12. Action：探索空間全体の評価 ⼊⼒と出⼒の関係 𝒙! ∶ ( 𝑥! ! ,𝑥" ! , ⋯ , 𝑥# ! )$ −−→ 𝑦! −−→ 𝑡! 𝒙" ∶ ( 𝑥! " , 𝑥" " , ⋯ , 𝑥# " )$ −−→ 𝑦" −−→ 𝑡" ⋮ 𝒙% : ( 𝑥! % , 𝑥" % , ⋯ , 𝑥# % )$ −−→ 𝑦% −−→ 𝑡% ⼊⼒ 真の関数値 実現値(観測値) ブ ラ ッ ク ボ ッ ク ス 関 数 ノ イ ズ
- 13. モデリング Action：探索空間全体の評価 𝒙! 𝝓(𝒙 𝒌 )様々な基底 関数に⼊⼒ 𝒘~$(𝟎,(!"𝑰#) 𝑦!重みづけして、各関数を結合 →スカラの関数値yを出⼒ 𝑡!ノイズ~𝑁(𝟎, 𝛽!" 𝑰#) 𝜙! 𝒙 𝒌 𝜙"(𝒙 𝒌 ) ⋮ 𝜙'(𝒙 𝒌 ) ブラックボックス関数
- 14. 諸々の定義𝒙 𝟏 ~ 𝒙𝑵 : ⼊⼒(ハイパーパラメータ群) 𝒚 𝑵 : ( 𝑦# , 𝑦$ , ⋯ , 𝑦% )& N点の真の関数値ベクトル 𝒕 𝑵 : ( 𝑡# , 𝑡$ , ⋯ , 𝑡% )& N点の実現値ベクトル 𝜙# ~ 𝜙': 基底関数群 𝜱 = 𝜙#(𝒙 𝟏 ) 𝜙$(𝒙 𝟏 ) 𝜙#(𝒙 𝟐 ) 𝜙$(𝒙 𝟐 ) … 𝜙'(𝒙 𝟏 ) … 𝜙'(𝒙 𝟐 ) ⋮ ⋮ 𝜙#(𝒙 𝑵 ) 𝜙$(𝒙 𝑵 ) ⋱ ⋮ … 𝜙'(𝒙 𝑵 ) 𝒌 = (𝑘 𝒙 𝟏 , 𝒙 𝑵)𝟏 , 𝑘 𝒙 𝟐 , 𝒙 𝑵)𝟏 , ⋯ , 𝑘 𝒙 𝑵 , 𝒙 𝑵)𝟏 )& i⾏⽬をベクトル化 𝜙(𝒙𝒊 ) 𝑘 𝒙𝒊 , 𝒙𝒋 = 𝛼*! 𝜙(𝒙𝒊 )$ 𝜙(𝒙𝒋 ) Φのカーネル関数
- 15. 𝒙 𝟏 ~𝒙 𝑵 ,𝒕 𝑵 (𝑡# ~𝑡% )を知ったうえで、次に追加する未知な点𝒙 𝑵)𝟏 の評価値の実現値が 𝑡 となる確率 𝑃 𝑡 𝒕 𝑵 )の分布は正規分布となり、 その平均と分散は以下のように𝒙 𝑵)𝟏 の関数としてあらわされる。 𝝁 𝒙 𝑵)𝟏 = 𝛼*# 𝒌𝚽𝚽 𝑻 𝒕 𝑵 𝝈 𝒙 𝑵)𝟏 = 𝑘 𝒙 𝑵)𝟏 , 𝒙 𝑵)𝟏 + 𝛽*# − 𝒌 𝑻 𝑪 𝑵 *𝟏 𝒌 Action：探索空間全体の評価 これによって、空間全体の評価値(実現値)の分布が特定できた。
- 16. Plan : 探索点の決定 全点の評価値の分布が分かった→ ではどの点を次に選ぶか？ • PI戦略(Probability of Improvement) • EI戦略(Expected Improvement) • UCB戦略(Upper Confidence Band) (LCB戦略(Lower Confidence Band)) これらに基づいた評価関数を獲得関数と呼ぶ
- 17. • PI戦略：現在の最⼤評価値を超える確率が最⼤である点を選ぶ 現在の最⼤評価値𝑡$%& 次の探索点に決定 Plan :探索点の決定 𝑃𝐼 𝑋 = 𝑎𝑟𝑔max *∈, {/ -!"# . 𝑝 𝑡 𝒕 𝑵) 𝑑𝑡}
- 18. • EI戦略：現在の最⼤評価値との差の期待値が最⼤の点を選ぶ 次の探索点に決定 𝐸𝐼 𝑋= 𝑎𝑟𝑔max *∈, 𝐸 𝑡 − 𝑡01* = 𝑎𝑟𝑔max *∈, {𝜇 − 𝑡01*} 最⼤評価値との差の期待値 分布の平均との距離 Plan : 探索点の決定 現在の最⼤評価値𝑡$%&
- 19. • U(L)CB戦略：信頼区間の上限(下限)が最⼤となる点を選ぶ 次の探索点に決定 Plan :探索点の決定 𝐸𝐼 𝑋 = 𝑎𝑟𝑔max *∈, 𝜇 + 2𝜎 平均から𝜎⼆つ分でおおよそ95%点 最適解にたどり着く理論的保証がある
- 20.
- 21. 𝝓の決め⽅ • 説明を⾶ばしたが、空間全体評価の際に登場する𝝓(基底関数群)も別に 決める必要がある。 • ただし、アルゴリズムの中では𝜙を⽤いたカーネル関数のみしか考えて いないため𝜙#~𝜙'をすべて⼀つ⼀つ決める必要はない。 (Φは登場するが、ΦΦ3(= グラム行列)として現れるので、これもカーネル関数の みで⼗分である) • 従ってこのカーネル関数を定義するだけでよい。(=カーネルトリック) ＊カーネル関数： (𝑘 𝒙𝒊, 𝒙𝒋 = 𝛼#$ 𝜙(𝒙𝒊)% 𝜙(𝒙𝒋)のように２ベクトルの⼊⼒から⼀つのスカラを返す関数) ＊
- 22. カーネルの種類 • Squared ExponentialKernel 𝑘!" 𝑥# , 𝑥$ = exp − 𝑥# − 𝑥$ % 2𝑙% • Matern Kernel 𝑘&'()*+ 𝑥# , 𝑥$ = 2,-. Γ(𝜈) ( 2𝜈 𝑥# − 𝑥$ 𝑙 ). 𝐾.( 2𝜈 𝑥# − 𝑥$ 𝑙 ) など カーネル法全般の解説：http://enakai00.hatenablog.com/entry/2017/10/13/145337
- 23. 実装： GPyOptでXgboostのハイパーパラメータ最適化 def blackbox(x): learning_rate =float(x[:,0]) subsample = float(x[:,1]) colsample_bytree = float(x[:,2]) gamma = float(x[:,3]) reg_lambda = float(x[:,4]) max_depth = int(x[:,5]) n_estimators = int(x[:,6]) XGB_instance = xgb.XGBRegressor(learning_rate = learning_rate, subsample = subsample, colsample_bytree = colsample_bytree, gamma = gamma, reg_lambda = reg_lambda, max_depth = max_depth, n_estimators = n_estimators, objective = "reg:linear") scores = cross_val_score(XGB_instance,X_train,y_train,cv=4,scoring='mean_squared_errorʻ) return -scores.mean() xは1×nの⼆次元リス トで渡されるので、各 パラメータを型変換 渡されたハイパーパ ラメータでインスタ ンス化 sklearnの cross_val_scoreで 評価値を計算 ・機械学習の⼀連の流れを関数として定義
- 24. 実装： GPyOptでXgboostのハイパーパラメータ最適化 ・探索してほしいハイパーパラメータの名前と値の範囲、連続or離散を以下のように定義 bounds = [{'name':'learning_rate','type': 'continuous', 'domain': (0.0005,0.3)}, {'name': 'sub_sample','type': 'continuous', 'domain': (0.5,1)}, {'name': 'colsample_bytree','type': 'continuous', 'domain': (0.5,1)}, {'name': 'gamma','type': 'continuous', 'domain': (0,1)}, {'name': 'reg_lambda','type': 'continuous', 'domain': (0,1)}, {'name': 'max_depth','type': 'discrete', 'domain': tuple(list(range(3,8)))}, {'name': 'n_estimator','type': 'discrete', 'domain': tuple(list(range(30,210,10)))}] continuous:連続 discrete：離散 （continuous→discreteの順でないとエラーになる）
- 25. 実装： GPyOptでXgboostのハイパーパラメータ最適化 ・最適化を⾏うクラスをインスタンス化し、run_optimizeメソッドで最適化を実⾏ initial_design_numdata：初期探索の回数 acquisition_type：獲得関数の設定 max_iter：最⼤探索回数 XGB_Bopt = GPyOpt.methods.BayesianOptimization(f=blackbox, domain=bounds, initial_design_numdata=5, acquisition_type='LCB') XGB_Bopt.run_optimization(max_iter=15) ・最適化終了後、x_opt,fx_optメソッドで最適解、最適値を出⼒ print(XGB_Bopt.x_opt,XGB_Bopt.fx_opt) → array([ 0.20040502, 0.68832784, 0.66486351, 0.81031615, 0.66657359, 5, 140. ]),array([ 0.50715448])
- 26.