More Related Content
PDF
PDF
PPTX
マルコフ連鎖モンテカルロ法 (2/3はベイズ推定の話) PDF
PDF
PPTX
PDF
PDF
What's hot
PDF
PDF
PPTX
StanとRでベイズ統計モデリング読書会(Osaka.stan) 第6章 PDF
PDF
PPTX
PDF
PDF
PDF
PDF
PPTX
PDF
PPTX
PDF
PDF
PDF
MCMCサンプルの使い方 ~見る・決める・探す・発生させる~ PPTX
PDF
Control as Inference (強化学習とベイズ統計) PDF
StanとRでベイズ統計モデリング 11章 離散値をとるパラメータ PPTX
Sliced Wasserstein距離と生成モデル Similar to レプリカ交換モンテカルロ法で乱数の生成
PPTX
PDF
MCMCとともだちになろう【※Docswellにも同じものを上げています】 PDF
クラシックな機械学習の入門 10. マルコフ連鎖モンテカルロ 法 PDF
MLaPP 24章 「マルコフ連鎖モンテカルロ法 (MCMC) による推論」 PDF
渡辺澄夫著「ベイズ統計の理論と方法」5.1 マルコフ連鎖モンテカルロ法 PDF
Monte Carlo Methods (Chapter 17 in Deep learning by Ian Goodfellow) PDF
PDF
PDF
PDF
ベイズ推定でパラメータリスクを捉える&優れたサンプラーとしてのMCMC PPTX
PDF
PDF
RBM、Deep Learningと学習(全脳アーキテクチャ若手の会 第3回DL勉強会発表資料) PDF
PDF
PDF
RStanとShinyStanによるベイズ統計モデリング入門 PDF
Infomation geometry(overview) PDF
基礎からのベイズ統計学 輪読会資料 第4章 メトロポリス・ヘイスティングス法 PDF
PRML Chapter 11 (11.0-11.2) PDF
More from Nagi Teramo
PDF
PDF
PPTX
Reproducebility 100倍 Dockerマン PDF
healthplanetパッケージで�体組成データを手に入れて�健康な体も手に入れる PDF
PDF
PDF
続わかりやすいパターン認識11章(11.1 - 11.4) PDF
PDF
PDF
PDF
PDF
東京R非公式おじさんが教える本当に気持ちいいパッケージ作成法 PDF
PDF
Trading volume mapping R in recent environment PDF
~knitr+pandocではじめる~『R MarkdownでReproducible Research』 PDF
PDF
可視化周辺の進化がヤヴァイ~rChartsを中心として~ PDF
「plyrパッケージで君も前処理スタ☆」改め「plyrパッケージ徹底入門」 PDF
Tokyo.R 白熱教室「これからのRcppの話をしよう」 PDF
レプリカ交換モンテカルロ法で乱数の生成
- 1.
第5回Tokyo. ciPy
レプリカ交換モンテカルロ法
で乱数の生成
@teramonagi
- 2.
目次
1. 自己紹介
2. モチベーション
3. マルコフ連鎖モンテカルロ法
4. レプリカ交換モンテカルロ法
5. まとめ
2
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
マルコフ連鎖モンテカルロ法
• 略して
–MCMC(Markov Chain MonteCarlo)
• 指定した確率(密度)関数に従う乱
数をマルコフ連鎖を活用することで
生成するモンテカルロ法のこと
• かなり汎用的な枠組み
9
- 10.
- 11.
- 12.
- 13.
- 14.
MCMC(メトロポリス法)
1. #適当なサイズだけ回す
2. SIZE = 10000
3. #初期状態を生成
4. x = [initial()] * SIZE
5. for i in range(1,SIZE):
6. #①:現在の状態から次の状態(候補)を選定
7. x_proposed = propose_next(x[i])
8. #②:確率密度の比を計算,target=密度関数
9. ratio = target(x_proposed) / target(x[i])
10. #③:一様乱数と比較し、遷移 or 元の状態のままを決定
11. if(np.random.uniform(size=1) < ratio):
12. x[i] = x_proposed
13. else:
14. x[i] = x[i-1]
Code:メトロポリス法実装例 in python
14
- 15.
- 16.
- 17.
- 18.
実際のコード(一部)
1. #正規分布の平均値
2. MU = 3.0
3. #シミュレーション・サイズ
4. SIZE_SIMULATION = 10000
5. X0 = np.array([0,0])
6. #次候補の選定関数
7. propose_next = lambda x:x+0.5*np.random.normal(size=len(x))
8. #target関数&MCMCオブジェクト生成
9. target = generate_target(MU)
10. mcmc = pyremc.MCMC(X0, target, propose_next, 10)
11. #MCMC実行
12. x = X0
13. for i in range(SIZE_SIMULATION):
14. x = np.vstack((x, mcmc.next()))
15. plot_result(x, MU)
Code:シミュレーションコード一部抜粋 in python
18
- 19.
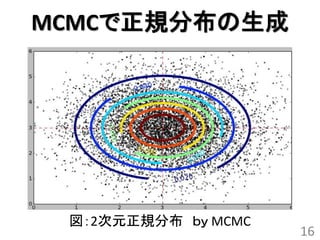
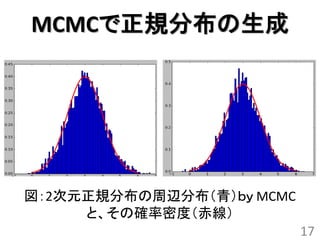
MCMCで正規分布生成
• 結果(概要)
–X方向:平均:3.05,標準偏差:1.03
–Y方向:平均:3.00,標準偏差:1.03
• うまくいっているように思える
• これはいい方法ダゾ!!!
19
- 20.
- 21.
- 22.
MCMCで混合正規分布生成
• 2次元の混合正規分布を生成
–混合数:2
–パラメータ
1 0
1 , 1 , w1 2,2,
,0.3
0 1
1 0
2 , 2 , w2 2,2,
,0.7
0 1
• メトロポリス法を10,000回試行
22
- 23.
- 24.
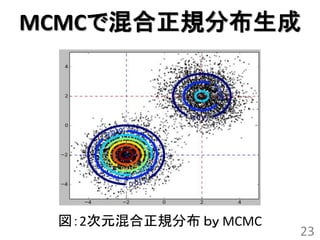
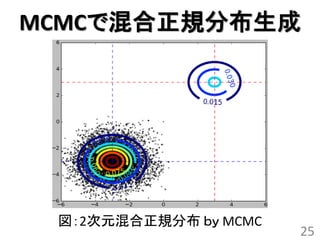
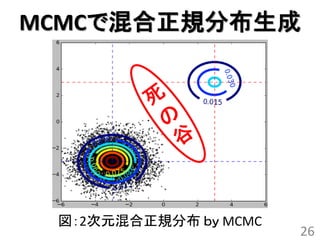
MCMCで混合正規分布生成
• 2次元の混合正規分布を生成
–混合数:2
–パラメータ
1 0
1 , 1 , w1 3,3,
,0.3
0 1
1 0
2 , 2 , w2 3,3,
,0.7
0 1
• メトロポリス法を10,000回試行
24
- 25.
- 26.
- 27.
- 28.
- 29.
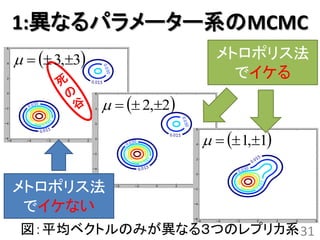
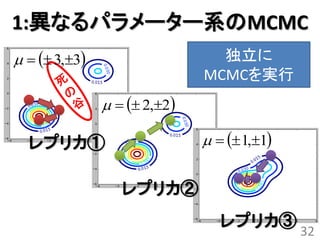
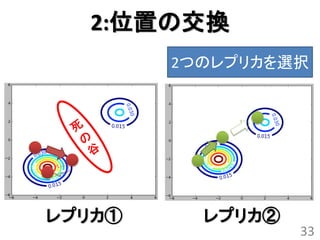
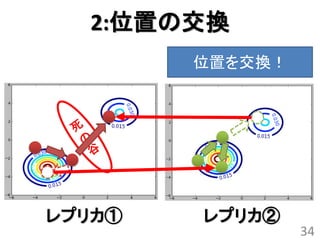
レプリカ交換モンテカルロ法
• 異なるパラメータを持つ確率分布(レプリカ)
を考えてそれらを交換するモンテカルロ法
–Replica Exchange MonteCarlo(REMC)
• 別名:パラレル・テンパリング法
• 元々はスピングラスのシミュレーション手法
– Hukushima-Nemoto, (1996), Multiple coupled Markov
chain MC , Parallel tempering
– Swendsen RH and Wang JS (1986) Replica Monte Carlo
simulation of spin glasses Physical Review Letters 57
29
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
REMCのコード
1. self._counter+=1
2. #①:全てのレプリカをMCMCで回す
3. for index_replica in range(self._replica_size):
4. self._mcmcs[index_replica].next()
5. #②:適当な交換頻度で位置の交換
6. if(self._counter % self._exchange_frequency == 0):
7. index_exchange = int(np.random.uniform(0,
self._replica_size-1))
8. x1 = self._mcmcs[index_exchange ].x
9. x2 = self._mcmcs[index_exchange+1].x
10. target1 = self._mcmcs[index_exchange ]._target
11. target2 = self._mcmcs[index_exchange+1]._target
12. #③:位置の交換はメトロポリス法に従う形で実行
13. if(np.random.uniform(size=1) <
(target1(x2)*target2(x1))/(target1(x1)*target2(x2))):
14. self._mcmcs[index_exchange].x,
self._mcmcs[index_exchange+1].x = np.copy(x2),np.copy(x1)
Code:REMC実装例(一部抜粋) in python 35
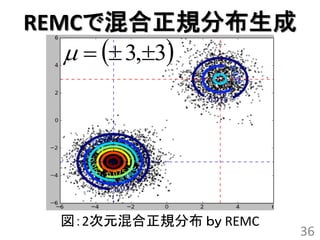
- 36.
- 37.
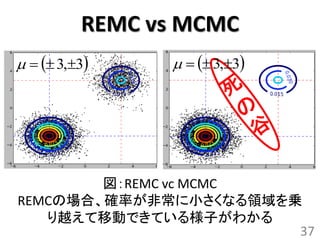
REMC vs MCMC
3,3 3,3
図:REMC vc MCMC
REMCの場合、確率が非常に小さくなる領域を乗
り越えて移動できている様子がわかる
37
- 38.
- 39.
- 40.
- 41.











![MCMC(メトロポリス法)
1. #適当なサイズだけ回す
2. SIZE = 10000
3. #初期状態を生成
4. x = [initial()] * SIZE
5. for i in range(1,SIZE):
6. #①:現在の状態から次の状態(候補)を選定
7. x_proposed = propose_next(x[i])
8. #②:確率密度の比を計算,target=密度関数
9. ratio = target(x_proposed) / target(x[i])
10. #③:一様乱数と比較し、遷移 or 元の状態のままを決定
11. if(np.random.uniform(size=1) < ratio):
12. x[i] = x_proposed
13. else:
14. x[i] = x[i-1]
Code:メトロポリス法実装例 in python
14](https://image.slidesharecdn.com/tokyoscipy520130126-130125162547-phpapp02/85/slide-14-320.jpg)

![実際のコード(一部)
1. #正規分布の平均値
2. MU = 3.0
3. #シミュレーション・サイズ
4. SIZE_SIMULATION = 10000
5. X0 = np.array([0,0])
6. #次候補の選定関数
7. propose_next = lambda x:x+0.5*np.random.normal(size=len(x))
8. #target関数&MCMCオブジェクト生成
9. target = generate_target(MU)
10. mcmc = pyremc.MCMC(X0, target, propose_next, 10)
11. #MCMC実行
12. x = X0
13. for i in range(SIZE_SIMULATION):
14. x = np.vstack((x, mcmc.next()))
15. plot_result(x, MU)
Code:シミュレーションコード一部抜粋 in python
18](https://image.slidesharecdn.com/tokyoscipy520130126-130125162547-phpapp02/85/slide-18-320.jpg)

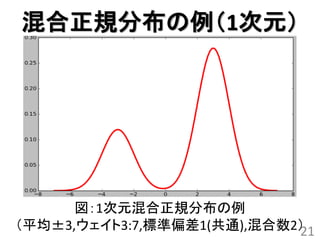
![混合正規分布
• 正規分布の重ね合わせで表現され
る分布 N
• 密度関数: px wi N x | i
i 1
• パラメータ
N : 正規分布の混合数
wi : 混合ウェイト([0,1])
20](https://image.slidesharecdn.com/tokyoscipy520130126-130125162547-phpapp02/85/slide-20-320.jpg)






![REMCのコード
1. self._counter+=1
2. #①:全てのレプリカをMCMCで回す
3. for index_replica in range(self._replica_size):
4. self._mcmcs[index_replica].next()
5. #②:適当な交換頻度で位置の交換
6. if(self._counter % self._exchange_frequency == 0):
7. index_exchange = int(np.random.uniform(0,
self._replica_size-1))
8. x1 = self._mcmcs[index_exchange ].x
9. x2 = self._mcmcs[index_exchange+1].x
10. target1 = self._mcmcs[index_exchange ]._target
11. target2 = self._mcmcs[index_exchange+1]._target
12. #③:位置の交換はメトロポリス法に従う形で実行
13. if(np.random.uniform(size=1) <
(target1(x2)*target2(x1))/(target1(x1)*target2(x2))):
14. self._mcmcs[index_exchange].x,
self._mcmcs[index_exchange+1].x = np.copy(x2),np.copy(x1)
Code:REMC実装例(一部抜粋) in python 35](https://image.slidesharecdn.com/tokyoscipy520130126-130125162547-phpapp02/85/slide-35-320.jpg)