Recommended
PPTX
OpenFOAMによる気液2相流解析の基礎と設定例
PDF
PDF
PDF
OpenFOAM の Function Object 機能について
PDF
PDF
PDF
PDF
OpenFOAM の cyclic、cyclicAMI、cyclicACMI 条件について
PDF
OpenFOAMにおけるDEM計算の力モデルの解読
PDF
OpenFoamの混相流solver interFoamのパラメータによる解の変化
PDF
OpenFOAMにおけるDEM計算の衝突モデルの解読
PDF
Turbulence Models in OpenFOAM
PPTX
PDF
OpenFOAMの混相流用改造solver(S-CLSVOF法)の設定・使い方
PDF
About multiphaseEulerFoam
PDF
ParaviewでのParticle Tracerを用いた可視化
PDF
PDF
Boundary Conditions in OpenFOAM
PDF
OpenFOAMを用いた計算後の等高面データの取得方法
PDF
OpenFOAM -回転領域を含む流体計算 (Rotating Geometry)-
PDF
PDF
OpenFOAMに実装したS-CLSVOF法検証(静止気泡のLaplace圧)
PDF
PDF
OpenFOAM を用いた Adjoint 形状最適化事例1
PDF
OpenFOAM -空間の離散化と係数行列の取り扱い(Spatial Discretization and Coefficient Matrix)-
PDF
PDF
OpenFOAM v2.3.0のチュートリアル 『oscillatingInletACMI2D』
PDF
About dexcs2021 for OpenFOAM
PDF
OpenFOAMのDEM解析のpatchInteractionModelクラスの解読
PDF
Setting and Usage of OpenFOAM multiphase solver (S-CLSVOF)
More Related Content
PPTX
OpenFOAMによる気液2相流解析の基礎と設定例
PDF
PDF
PDF
OpenFOAM の Function Object 機能について
PDF
PDF
PDF
PDF
OpenFOAM の cyclic、cyclicAMI、cyclicACMI 条件について
What's hot
PDF
OpenFOAMにおけるDEM計算の力モデルの解読
PDF
OpenFoamの混相流solver interFoamのパラメータによる解の変化
PDF
OpenFOAMにおけるDEM計算の衝突モデルの解読
PDF
Turbulence Models in OpenFOAM
PPTX
PDF
OpenFOAMの混相流用改造solver(S-CLSVOF法)の設定・使い方
PDF
About multiphaseEulerFoam
PDF
ParaviewでのParticle Tracerを用いた可視化
PDF
PDF
Boundary Conditions in OpenFOAM
PDF
OpenFOAMを用いた計算後の等高面データの取得方法
PDF
OpenFOAM -回転領域を含む流体計算 (Rotating Geometry)-
PDF
PDF
OpenFOAMに実装したS-CLSVOF法検証(静止気泡のLaplace圧)
PDF
PDF
OpenFOAM を用いた Adjoint 形状最適化事例1
PDF
OpenFOAM -空間の離散化と係数行列の取り扱い(Spatial Discretization and Coefficient Matrix)-
PDF
PDF
OpenFOAM v2.3.0のチュートリアル 『oscillatingInletACMI2D』
PDF
About dexcs2021 for OpenFOAM
Viewers also liked
PDF
OpenFOAMのDEM解析のpatchInteractionModelクラスの解読
PDF
Setting and Usage of OpenFOAM multiphase solver (S-CLSVOF)
PDF
How to get contour surface position by openfoam
PDF
PDF
PDF
Estimation of numerical schemes in heat convection by OpenFOAM
PDF
PDF
Spatial Interpolation Schemes in OpenFOAM
Similar to OpenFOAMにおける混相流計算
PDF
PDF
PDF
「輸送方程式のソース項の実装 Ver-2.1の新機能Field sources」OpenFOAM勉強会 for beginner@関東,2012年04月21日
PPT
PDF
OpenFOAM+のCo-simulation機能とFMUの試作
PDF
PDF
rhoCentralFoam in OpenFOAM
PDF
blockCoupledSwirlTestチュートリアル
PDF
PDF
PDF
ADVENTUREの他のモジュール・関連プロジェクトの紹介
PPTX
PDF
配管流路の多目的最適化OpenFOAM+OpenMDAO(第28回オープンCAE勉強会@関西)
PDF
オープンソースの CFD ソフトウェア SU2 のチュートリアルをやってみた
PDF
ADVENTUREの他のモジュール・関連プロジェクトの紹介
PDF
PDF
20211023_StirredTankrRactor 1
PDF
PPTX
FSI analysis with preCICE (OpenFOAM and CalculiX)
PPTX
手描き感を再現する�ペイントシミュレータの最新研究紹介
OpenFOAMにおける混相流計算 1. 2. 3. 混相流流の数値計算法
混相流のシミュレーションを分類すると以下の通りになる
• メッシュフリー法
• 界面捕獲法 (Interface
Tracking)
• 界面追跡法 (Interface
Capturing)
• 平均化(二流体)モデル
• メッシュフリー法
粒子法(MPS,
SPH)
• 界面捕獲法
VOF法
Level-‐Set法
Phase
Field法
• 界面追跡法
BFC(界面適合座標)
ALE(Arbitrary
Lagrangian-‐Eulerian)
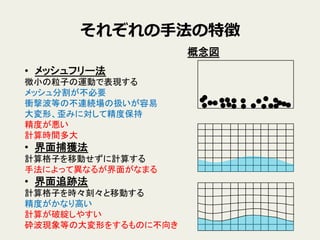
4. それぞれの⼿手法の特徴
• メッシュフリー法
微小の粒子の運動で表現する
メッシュ分割が不必要
衝撃波等の不連続場の扱いが容易
大変形、歪みに対して精度保持
精度が悪い
計算時間多大
• 界面捕獲法
計算格子を移動せずに計算する
手法によって異なるが界面がなまる
• 界面追跡法
計算格子を時々刻々と移動する
精度がかなり高い
計算が破綻しやすい
砕波現象等の大変形をするものに不向き
概念図
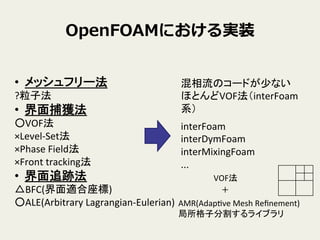
5. OpenFOAMにおける実装
• メッシュフリー法
?粒子法
• 界面捕獲法
○VOF法
×Level-‐Set法
×Phase
Field法
×Front
tracking法
• 界面追跡法
△BFC(界面適合座標)
○ALE(Arbitrary
Lagrangian-‐Eulerian)
混相流のコードが少ない
ほとんどVOF法(interFoam
系)
interFoam
interDymFoam
interMixingFoam
...
AMR(AdapVve
Mesh
Refinement)
局所格子分割するライブラリ
VOF法
+
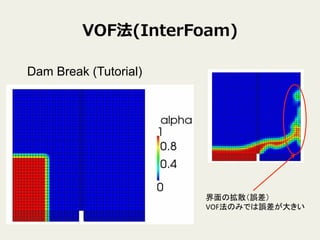
6. VOF(Volume of Fluid)法
• ⽀支配⽅方程式
Navier-‐‑‒Stokes 式
連続式
流流体率率率αの移流流⽅方程式
sk
gP
t
δσ
ρν
σ
σ
nF
Fvvv
v
=
++∇+−∇=∇⋅+
∂
∂ 2
0=⋅∇ v
• VOF法の欠点
界面の形状が明確に定義されな
い
• VOF法の長所
境界面の複雑な変形を伴う現象
をシミュレート可能
アルゴリズムが単純
現在の研究ではVOF法を解くの
みの研究は少ない
VOF法と様々なものを組み合わせ
てシミュレーション
k:
界面の曲率
::
liquid
phase
::
interface
::
gas
phase
1=α
0=α
10 <<α
( ) 0=⋅∇+
∂
∂
vα
α
t
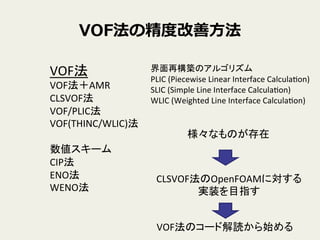
7. VOF法の精度度改善⽅方法
VOF法
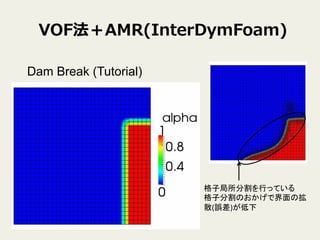
VOF法+AMR
CLSVOF法
VOF/PLIC法
VOF/SLIC法
VOF/WLIC法
VOF/IB法
数値スキーム
CIP法
WENO法
界面再構築のアルゴリズム
PLIC
(Piecewise
Linear
Interface
CalculaVon)
SLIC
(Simple
Line
Interface
CalculaVon)
WLIC
(Weighted
Line
Interface
CalculaVon)
様々なものが存在
洋書
2011年出版(初版)
Cambridge
Univ.
Press
混相流の計算手法について
(主にVOF系,
Front-‐Tracking,
Level-‐Set
など)
8. 9. 10. VOF法の精度度改善⽅方法
VOF法
VOF法+AMR
CLSVOF法
VOF/PLIC法
VOF(THINC/WLIC)法
数値スキーム
CIP法
ENO法
WENO法
界面再構築のアルゴリズム
PLIC
(Piecewise
Linear
Interface
CalculaVon)
SLIC
(Simple
Line
Interface
CalculaVon)
WLIC
(Weighted
Line
Interface
CalculaVon)
様々なものが存在
CLSVOF法のOpenFOAMに対する
実装を目指す
VOF法のコード解読から始める
11. //
Need
to
store
rho
for
ddt(rho,
U)
volScalarField
rho
(
IOobject
(
"rho",
runTime.VmeName(),
mesh,
IOobject::READ_IF_PRESENT
),
alpha1*rho1
+
(scalar(1)
-‐
alpha1)*rho2,
alpha1.boundaryField().types()
);
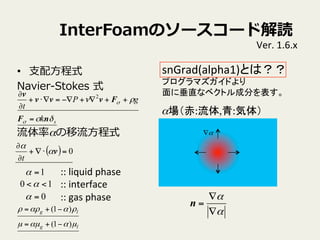
InterFoamのソースコード解読
• ⽀支配⽅方程式
Navier-‐‑‒Stokes 式
流流体率率率αの移流流⽅方程式
sk
gP
t
δσ
ρν
σ
σ
nF
Fvvv
v
=
++∇+−∇=∇⋅+
∂
∂ 2
::
liquid
phase
::
interface
::
gas
phase
1=α
0=α
10 <<α
lg
lg
µααµµ
ρααρρ
)1(
)1(
−+=
−+=
lg ρααρρ )1( −+=
createFields.Hの中
Ver.
1.6.x
( ) 0=⋅∇+
∂
∂
vα
α
t
12. InterFoamのソースコード解読
• ⽀支配⽅方程式
Navier-‐‑‒Stokes 式
流流体率率率αの移流流⽅方程式
sk
gP
t
δσ
ρν
σ
σ
nF
Fvvv
v
=
++∇+−∇=∇⋅+
∂
∂ 2
::
liquid
phase
::
interface
::
gas
phase
1=α
0=α
10 <<α
lg
lg
µααµµ
ρααρρ
)1(
)1(
−+=
−+=
Ver.
1.6.x
lg µααµµ )1( −+=
/src/transportModels/incompressible/
incompressibleTwoPhaseMixture/
twoPhaseMixture.C
118行目
tmp<volScalarField>
twoPhaseMixture::mu()
const
{
volScalarField
limitedAlpha1
=
min(max(alpha1_,
scalar(0)),
scalar(1));
return
tmp<volScalarField>
(
new
volScalarField
(
"mu",
limitedAlpha1*rho1_*nuModel1_-‐>nu()
+
(scalar(1)
-‐
limitedAlpha1)*rho2_*nuModel2_-‐>nu()
)
);
}
( ) 0=⋅∇+
∂
∂
vα
α
t
13. 14. 15. 16.
Ueqn.H中
19行目
if
(momentumPredictor)
{
solve
(
UEqn
==
fvc::reconstruct
(
fvc::interpolate(rho)*(g
&
mesh.Sf())
+
(
fvc::interpolate(interface.sigmaK())*fvc::snGrad(alpha1)
-‐
fvc::snGrad(p)
)
*
mesh.magSf()
)
);
}
InterFoamのソースコード解読
• ⽀支配⽅方程式
Navier-‐‑‒Stokes 式
流流体率率率αの移流流⽅方程式
::
liquid
phase
::
interface
::
gas
phase
1=α
0=α
10 <<α
Ver.
1.6.x
sk δσσ nF =
sk
gP
t
δσ
ρν
σ
σ
nF
Fvvv
v
=
++∇+−∇=∇⋅+
∂
∂ 2
( ) 0=⋅∇+
∂
∂
vα
α
t
lg
lg
µααµµ
ρααρρ
)1(
)1(
−+=
−+=
sigmaK()とは??
snGrad(alpha1)とは??
fvc::reconstructとは??
17. InterFoamのソースコード解読
• ⽀支配⽅方程式
Navier-‐‑‒Stokes 式
流流体率率率αの移流流⽅方程式
::
liquid
phase
::
interface
::
gas
phase
1=α
0=α
10 <<α
Ver.
1.6.x
( ) 0=⋅∇+
∂
∂
vα
α
t
lg
lg
µααµµ
ρααρρ
)1(
)1(
−+=
−+=
sigmaK()とは??
interfaceProperVes.H 中
140行目
tmp<volScalarField>
sigmaK()
const
{
return
sigma_*K_;
}
sigma_
:surface
tension
K_
:curvature
sigmaK()
skF δσσ n=
sk
gP
t
δσ
ρν
σ
σ
nF
Fvvv
v
=
++∇+−∇=∇⋅+
∂
∂ 2
18. 19. InterFoamのソースコード解読
• ⽀支配⽅方程式
Navier-‐‑‒Stokes 式
流流体率率率αの移流流⽅方程式
::
liquid
phase
::
interface
::
gas
phase
1=α
0=α
10 <<α
Ver.
1.6.x
( ) 0=⋅∇+
∂
∂
vα
α
t
lg
lg
µααµµ
ρααρρ
)1(
)1(
−+=
−+=
sk
gP
t
δσ
ρν
σ
σ
nF
Fvvv
v
=
++∇+−∇=∇⋅+
∂
∂ 2
fvc::interpolate(interface.sigmaK())*fvc::snGrad(alpha1)
Fσ =σknδs
表面張力モデルCSFモデル
n =
∇α
∇α
δs = ∇a
Fσ =σk∇α
Ueqn.H中
20. fvc::reconstructとは??
OpenFOAM
wiki
+
CFD
onlineより
InterFoamのソースコード解読
• ⽀支配⽅方程式
Navier-‐‑‒Stokes 式
流流体率率率αの移流流⽅方程式
::
liquid
phase
::
interface
::
gas
phase
1=α
0=α
10 <<α
Ver.
1.6.x
( ) 0=⋅∇+
∂
∂
vα
α
t
lg
lg
µααµµ
ρααρρ
)1(
)1(
−+=
−+=
sk
gP
t
δσ
ρν
σ
σ
nF
Fvvv
v
=
++∇+−∇=∇⋅+
∂
∂ 2
hpp://www.cfd-‐online.com/Forums/openfoam-‐programming-‐
development/77943-‐fvc-‐reconstruct-‐algorithm.html
hpps://openfoamwiki.net/index.php/OpenFOAM_guide/
ReconstrucVon
セル界面でのFluxからセル中心での速度
ベクトルを返す。
output
=
fvc::reconstruct(input)
output
::
セル中心での速度ベクトル
input
::
セル界面でのFlux
目的:
圧力振動を生じさせないように、擬
似的なスタッガード格子のように作用させ
るため。
21. InterFoamのソースコード解読
Ver.
1.6.x
α式の設定
( ) ( )( ) 01 =−⋅∇+⋅∇+
∂
∂
r
t
vv ααα
α
最終形
(微分形)
有限体積法なので
積分系に変換
積分系
( ) ( )( ) 01 =−⋅∇+⋅∇+ ∫∫∫ ΔΔΔ
dVdVdV
dt
d
V
r
VV
vv αααα
ガウスの発散定理
dVds
Vs ∫∫ ⋅∇=⋅ aan
( ) dSdSdV
dt
d
SSV ∫∫∫ ⋅−+⋅+
Δ
nvnv rαααα 1
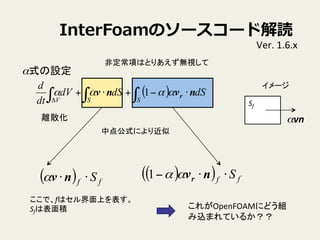
22. InterFoamのソースコード解読
Ver.
1.6.x
α式の設定
( ) dSdSdV
dt
d
SSV ∫∫∫ ⋅−+⋅+
Δ
nvnv rαααα 1
離散化
非定常項はとりあえず無視して
( )( ) ff S⋅⋅− nvrαα1( ) ff S⋅⋅nvα
ここで、fはセル界面上を表す。
Sfは表面積
中点公式により近似
Sf
αvn
イメージ
これがOpenFOAMにどう組
み込まれているか??
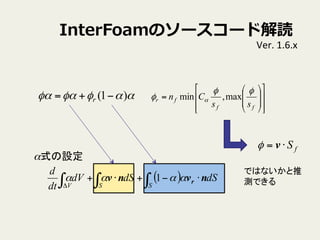
23. InterFoamのソースコード解読
Ver.
1.6.x
alphaEqn.H
中
5~8行目
surfaceScalarField
phic
=
mag(phi/mesh.magSf());
phic
=
min(interface.cAlpha()*phic,
max(phic));
surfaceScalarField
phir
=
phic*interface.nHat();
f
c
S
φ
φ =
))max(,min( ccc C φφφ α ×=
fcr n×=φφ
それぞれ
代入
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
ff
fr
ss
Cn
φφ
φ α max,min
プログラム上では
( )( ) ff S⋅⋅− nvrαα1
文字rから判断すると??
24. InterFoamのソースコード解読
Ver.
1.6.x
alphaEqn.H
中
5~8行目
surfaceScalarField
phic
=
mag(phi/mesh.magSf());
phic
=
min(interface.cAlpha()*phic,
max(phic));
surfaceScalarField
phir
=
phic*interface.nHat();
find,
grepでソース(src)内検索
src/transportModels/interfaceProperVes/interfaceProperVes.C
中
cAlpha,
nHat_,
K_等の設定
25. InterFoamのソースコード解読
Ver.
1.6.x
//
Face
unit
interface
normal
flux
nHat_
=
nHatv
&
Sf;
//
Simple
expression
for
curvature
K_
=
-‐fvc::div(nHat_);
transportProperVesDict_(dict),
cAlpha_
(
readScalar
(
alpha1.mesh().soluVonDict().subDict("PISO").lookup("cAlpha")
)
),
src/transportModels/interfaceProperVes/interfaceProperVes.C 中
ffvf Snn ⋅=
表面張力モデルCSFモデル
(Brackbill
(1992))
(ConVnuum
Surface
Force)
Fσ =σknδs
k = ∇⋅nf
k = ∇⋅n
n
Cαの読み込み
131行目
117行目
146行目
26. InterFoamのソースコード解読
Ver.
1.6.x
//
Face
unit
interface
normal
surfaceVectorField
nHatv
=
gradAlphaf/
(mag(gradAlphaf)
+
deltaN_);
src/transportModels/interfaceProperVes/interfaceProperVes.C 中
113行目
nfv =
∇α( )f
∇α( )f
+δN
deltaN_
(
"deltaN",
1e-‐8/pow(average(alpha1.mesh().V()),
1.0/3.0)
),
156行目
δN =
1.0×10−8
( Vi / N
N
∑ )1/3
界面の法線方向計算の安定化
(ゼロ割を防ぐ)
27. InterFoamのソースコード解読
Ver.
1.6.x
alphaEqn.H
中
5~8行目
surfaceScalarField
phic
=
mag(phi/mesh.magSf());
phic
=
min(interface.cAlpha()*phic,
max(phic));
surfaceScalarField
phir
=
phic*interface.nHat();
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
ff
fr
ss
Cn
φφ
φ α max,min
( )( ) ff S⋅⋅− nvrαα1
最初の推測
なんとなく
それっぽいという所までの理解
28. InterFoamのソースコード解読
Ver.
1.6.x
alphaEqn.H
中
9行目~
for
(int
aCorr=0;
aCorr<nAlphaCorr;
aCorr++)
{
surfaceScalarField
phiAlpha
=
fvc::flux
(
phi,
alpha1,
alphaScheme
)
+
fvc::flux
(
-‐fvc::flux(-‐phir,
scalar(1)
-‐
alpha1,
alpharScheme),
alpha1,
alpharScheme
);
MULES::explicitSolve(alpha1,
phi,
phiAlpha,
1,
0);
rhoPhi
=
phiAlpha*(rho1
-‐
rho2)
+
phi*rho2;
}
Fvc::flux
流束を返す。
/src/finiteVolume/finiteVolume/
fvc/fvcFlux.c中
φα
ααφ )1( −r
ααφφαφα )1( −+= r
プログラム上では
MULES(MulVdimensional
Universal
Limiter
for
Explicit
SoluVon)??
29. 30. ( )( ) ff
S⋅⋅− nvrαα1
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛ ⋅⋅
f
ff
f
ff
f
S
Su
S
Su
Cn max,min α
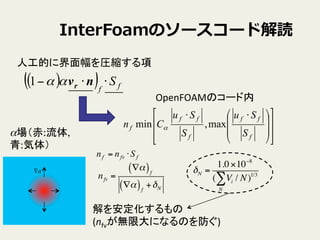
OpenFOAMのコード内
nfv =
∇α( )f
∇α( )f
+δN
δN =
1.0×10−8
( Vi / N
N
∑ )1/3
解を安定化するもの
(nfvが無限大になるのを防ぐ)
人工的に界面幅を圧縮する項
ffvf Snn ⋅=
α場(赤:流体,
青:気体)
α∇
InterFoamのソースコード解読
31. 32. References
• J.
U.
Brackbill
et
al.,
J.
Comp.
Phys.,
100,
335-‐354
(1992).
• G.
Tryggvason
et
al.,
Direct
Numerical
SimulaVons
of
Gas-‐
Liquid
MulVphase
Flows
(Cambridge
University
Press,
2011)
• プログラマーズガイド
• OpenFOAM
wiki
(hpps://openfoamwiki.net/index.php/
OpenFOAM_guide/ReconstrucVon)
• CFD
online
(hpp://www.cfd-‐online.com/Forums/openfoam-‐
programming-‐development/77943-‐fvc-‐reconstruct-‐algorithm.html)