Download as PDF, PPTX
![使い⽅方(dam break)
cp
-‐r
$FOAM_TUTORIALS/mulYphase/interFoam/laminar/damBreak
.
damBreakフォルダをコピー
damBreakフォルダ内の編集
1. constant/transportProperYesの編集
transportProperYesの最後に以下を記入
deltaX
deltaX
[
0
0
0
0
0
0
0
]
0.01;
2. 初期条件にpsi(Level-‐Set関数)を追加
(alpha1を基に編集)
cp
-‐r
0/alpha1
0/psi
3. sclsVOFFoamのコマンド実行
(deltaXの値は界面付近で
のセルの一辺の幅)
psi内を編集(次元は無次元)](https://image.slidesharecdn.com/s-clsvofsolver-140603091744-phpapp02/85/OpenFOAM-solver-S-CLSVOF-13-320.jpg)
More Related Content
Similar to OpenFOAMの混相流用改造solver(S-CLSVOF法)の設定・使い方
OpenFOAMの混相流用改造solver(S-CLSVOF法)の設定・使い方
- 1. OpenFOAMの混相流流⽤用改 造solver(S-‐‑‒CLSVOF法) 設定・使い⽅方 ⼤大阪⼤大学⼤大学院基礎⼯工学研究科 物質創成専攻化学⼯工学領領域 博⼠士2年年 ⼭山本卓也 第42回OpenCAE勉強会@関西 (2015/10/17) Updated Ver. Update date 2015/10/17 第30回OpenCAE勉強会@関西 (2014/05/31) 第50回OpenCAE勉強会@関東(流体など) (2015/08/22)
- 2. 混相流流の数値計算法 混相流のシミュレーションを分類すると以下の通りになる • メッシュフリー法 • 界面捕獲法 (Interface Tracking) • 界面追跡法 (Interface Capturing) • 平均化(二流体)モデル • メッシュフリー法 粒子法(MPS, SPH) DEM • 界面捕獲法 VOF法 Level-‐Set法 Phase Field法 Front-‐Tracking法 • 界面追跡法 BFC(界面適合座標)
- 3. それぞれの⼿手法の特徴 • メッシュフリー法 微小の粒子の運動で表現する メッシュ分割が不必要 衝撃波等の不連続場の扱いが容易 大変形、歪みに対して精度保持 精度が悪い 計算時間多大 • 界面捕獲法 計算格子を移動せずに計算する 手法によって異なるが界面がなまる • 界面追跡法 計算格子を時々刻々と移動する 精度がかなり高い 計算が破綻しやすい 砕波現象等の大変形をするものに不向き 概念図
- 4. OpenFOAMにおける実装 • メッシュフリー法 ?粒子法 ○DEM • 界面捕獲法 ○VOF法 ×Level-‐Set法 ×Phase Field法 ×Front tracking法 • 界面追跡法 △BFC(界面適合座標) 混相流のコードが少ない ほとんどVOF法（interFoam 系） interFoam interDymFoam interMixingFoam ... AMR(AdapYve Mesh Refinement) 局所格子分割するライブラリ VOF法 ＋
- 5. VOF法の界⾯面再構築法 0 0 0 0 0 0 0 0 0.1 0.3 0 0 0.5 0.95 1.0 0 0.4 1.0 1.0 1.0 0 0.7 1.0 1.0 1.0 VOF 精度悪い 界面がなまりやすい
- 6.
- 7. S-‐‑‒CLSVOF法⽤用 solver(sclsVOFFoam)とは? • OpenFOAMのinterFoam(VOF法)を改良したsolver • 表面張力項(CSFモデル)の表面張力の加わる力の向きを Level-‐Set関数を用いて修正した。 • Level-‐Set法で見られるre-‐iniYalizaYon式を解くことによって 修正した。 • 具体的な計算例については前回までの関西勉強会資料を ご参照ください。 第25回OpenCAE勉強会@関西 第26回OpenCAE勉強会@関西 J. U. Brackbill, D. B. Kothe, C. Zemach, J. Comput. Phys. 100 (1992) 335–354.CSFモデル VOF法 C. W. Hirt, B. D. Nichols, J. Comput. Phys. 39 (1981) 201–225. S-‐CLSVOF(Simple Coupled Volume Of Fluid with Level Set)法 第30回OpenCAE勉強会@関西
- 8. 一般に Level-‐Set法 • 体積保存性悪 • 界面の法線ベクトル計算良 VOF法 • 体積保存性良 • 界面の法線ベクトル計算悪 M. Sussman, P. Smereka, S. Osher, J. Comput. Phys. 114 (1994) 146–159. CLSVOF(Coupled Volume Of Fluid with Level Set)法 S-‐CLSVOF(Simple Coupled Volume Of Fluid with Level Set)法 簡易な連成手法 高精度、しかし、体積保存性が少し悪い VOF法より精度改善、体積保存性良好 S-‐‑‒CLSVOF法⽤用 solver(sclsVOFFoam)とは?
- 9. S-‐‑‒CLSVOF法⽤用 solver(sclsVOFFoam)とは? 具体的に A. Albadawi et al., Int. J. MulYphase Flow, 53, 11-‐28 (2013). の論文に紹介されている手法(S-‐CLSVOF法)を導入し てみた。 • 表面張力(CSFモデル)の力の向きのみ修正 • Level-‐Set関数によってVOF関数(流体率)を修正しない
- 10. 0 0 0 0 0 0 0 0 0.1 0.3 0 0 0.5 0.95 1.0 0 0.4 1.0 1.0 1.0 0 0.7 1.0 1.0 1.0 VOF S-‐‑‒CLSVOF法⽤用 solver(sclsVOFFoam)とは? re-‐iniYalizaYon式 Level-‐Set関数
- 11. 対応Version in OpenFOAM • OpenFOAM-‐‑‒2.0.x • OpenFOAM-‐‑‒2.1.1 • OpenFOAM-‐‑‒2.1.x • OpenFOAM-‐‑‒2.2.x その他のVersionに関しては未検証 公開場所(bitBucket) haps://bitbucket.org/nunuma/public/src
- 12. 使い⽅方(solverのコンパイル) 1. sclsVOFFoamのsolverをapplicaYons/ solvers以下に置く(cp -‐r sclsVOFFoam applicaYons/solvers) 2. sclsVOFFoam内に移動(cd sclsVOFFoam) 3. ./Allwclean 4. ./Allwmake 5. コンパイルが完了 試しにターミナル上でsclsVOFFoamとタイプしてみてください
- 13. 使い⽅方(dam break) cp -‐r $FOAM_TUTORIALS/mulYphase/interFoam/laminar/damBreak . damBreakフォルダをコピー damBreakフォルダ内の編集 1. constant/transportProperYesの編集 transportProperYesの最後に以下を記入 deltaX deltaX [ 0 0 0 0 0 0 0 ] 0.01; 2. 初期条件にpsi(Level-‐Set関数)を追加 (alpha1を基に編集) cp -‐r 0/alpha1 0/psi 3. sclsVOFFoamのコマンド実行 (deltaXの値は界面付近で のセルの一辺の幅) psi内を編集(次元は無次元)
- 14. 使い⽅方(dam break) interFoamからの変更すべき点 1. 計算格子幅deltaXをtransportProperYes内に記入 2. Level-‐Set関数を初期条件(境界条件)へ導入 注意点 • Level-‐Set関数用の境界条件については現在未作成 (接触角を与える境界条件での使用不可) • Level-‐Set関数で複雑なことを行う際は境界条件を実装 する必要有り • Level-‐Set関数用境界条件も実装 • 静的接触角、動的接触角も使用可能に
- 15. 使い⽅方(dam break) walls { type constantAlphaContactAngle; theta0 45; limit gradient; value uniform 0; } 接触角境界条件 alpha1 walls { type constantPsiContactAngle; theta0 45; limit gradient; value uniform 0; } 接触角境界条件 psi constantAlphaContactAngleを constantPsiContactAngleに変更
- 16. 検証問題 2γ cosθE =ρgHR H = 2γ cosθE ρgR 解析解 物性値と計算条件 g : 1.00 x 101 m2/s γ : 7.07 x 10-‐2 N/m ρ : 1000 kg/m3 R : 1.00 x 10-‐3 m θE : 45o Hanal = 1.00 x 10-‐2 m
- 17. VOF S-‐CLSVOF 検証問題 Error = 7.745 % (VOF) = 6.229 % (S-‐CLSVOF) 未だに誤差が大きい
- 18. 誤差低減のために 用いているCSFモデルを密度ベースの方法に変更 (Density-‐scaled balanced CSF model) 大きな密度差によって大きな誤差(界面上での 大きなspurious current)が発生 K. Yokoi, J. Comp. Phys., 278, 221-228 (2014). 新しいsolverの作成(S-‐CLSVOF + Density-‐scaled balanced CSF model) sclsVOFDSBFoam
- 19. VOF S-‐CLSVOF 検証問題 Error = 7.745 % (VOF) = 6.229 % (S-‐CLSVOF) = 2.694 % (S-‐CLSVOF(DSB)) sclsVOFDSBFoamで かなり誤差が低減 S-‐CLSVOF(DSB)
- 20. 対応Version in OpenFOAM • OpenFOAM-‐‑‒2.0.x • OpenFOAM-‐‑‒2.1.1 • OpenFOAM-‐‑‒2.1.x • OpenFOAM-‐‑‒2.2.x その他のVersionに関しては未検証 公開場所(bitBucket) haps://bitbucket.org/nunuma/public/src/ e2a854864f95a274617f210e852f74ed64bd458f/OpenFOAM/?at=master
- 21. 使い⽅方(solverのコンパイル) 1. sclsVOFDSBFoamのsolverをapplicaYons/ solvers以下に置く(cp -‐r sclsVOFFoam applicaYons/solvers) 2. sclsVOFDSBFoam内に移動(cd sclsVOFFoam) 3. ./Allwclean 4. ./Allwmake 5. コンパイルが完了 試しにターミナル上でsclsVOFDSBFoamとタイプしてみてください
- 22. まとめ • sclsVOFFoam(S-‐‑‒CLSVOF 法),sclsVOFDSBFoam(S-‐‑‒CLSVOF法 +Density-‐‑‒scaled balanced CSFモデル )を⽤用いる際にはinterFoam(VOF法)に ⽤用いたケースディレクトリに計算格⼦子幅 とLevel-‐‑‒Set関数の記⼊入が必要 • 接触⾓角条件も実装 • interFoamのケースディレクトリより容 易易に計算可能
- 23. 今後の展望 • 汎⽤用性のあるコードに書き換え • interDymFoam(Dynamic Mesh)等に も対応できるようにVersion up予定 • ⾼高精度度スキーム等の開発予定 • 最新版のsolverに対しても実装予定
- 24. 参考⽂文献 1. G. Tryggvason,R. Scardovelli and S. Zaleski, Direct Numerical Simulations of Gas-Liquid Multiphase Flows, Cambridge University Press, Cambridge 2011. 2. C. W. Hirt, B. D. Nichols, J. Comput. Phys. 39 (1981) 201– 225. 3. J. U. Brackbill, D. B. Kothe and C. Zemach, J. Comput. Phys. 100 (1992) 335–354. 4. A. Albadawi et al., Int. J. Multiphase Flow 53 (2013) 11-28. 5. M. Sussman, P. Smereka and S. Osher, J. Comput. Phys. 114 (1994) 146–159. 6. K. Yokoi, J. Comp. Phys., 278, 221-228 (2014).
- 27.
- 28. interFoam (VOF法) • ⽀支配⽅方程式 Navier-‐‑‒Stokes 式 流流体率率率αの移流流⽅方程式 sk gP t δσ ρν σ σ nF Fvvv v = ++∇+−∇=∇⋅+ ∂ ∂ 2 :: liquid phase :: interface :: gas phase 1=α 0=α 10 <<α 液相領域 固相領域 ( ) 0=⋅∇+ ∂ ∂ l t vα α ( ) 0=⋅∇+ ∂ ∂ vα α t ( )( ) 01 =−⋅∇+ ∂ ∂ g t vα α 小文字l, gはそれぞれ液相、気相を表す。 ( ) glr gl vvv vvv −= −+= αα 1 vr: 相関速度（圧縮速度） 再定義 ρ =αρl +(1−α)ρg µ =αµl +(1−α)µg ( ) 0=⋅∇+ ∂ ∂ vα α t CSFモデル
- 29. • ⽀支配⽅方程式 Navier-‐‑‒Stokes 式 流流体率率率αの移流流⽅方程式 sk gP t δσ ρν σ σ nF Fvvv v = ++∇+−∇=∇⋅+ ∂ ∂2 :: liquid phase :: interface :: gas phase 1=α 0=α 10 <<α ( ) ( )( ) 01 =−⋅∇+⋅∇+ ∂ ∂ r t vv ααα α 最終形 alphaEqn.H中で設定 ∂α ∂t + ∇⋅ αv( )= 0 この項は界面上に働くもの (1-‐α)αが入っているため 実際の物理現象では界面厚み がないため数値計算のために 用いられる仮想的なもの interFoam (VOF法) ρ =αρl +(1−α)ρg µ =αµl +(1−α)µg
- 30. α式の設定 ( ) dSdSdV dt d SSV∫∫∫ ⋅−+⋅+ Δ nvnv rαααα 1 離散化 ( )( ) ff S⋅⋅− nvrαα1( ) ff S⋅⋅nvα ここで、fはセル界面上を表す。 Sfは表面積 中点公式により近似 Sf αvn イメージ ( ) ( )( ) 01 =−⋅∇+⋅∇+ ∂ ∂ r t vv ααα α 離散化（program中で解く形に変換） interFoam (VOF法) MULESでこのfluxを計算
- 31. ( )( )ff S⋅⋅− nvrαα1 ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⋅⋅ f ff f ff f S Su S Su Cn max,min α OpenFOAMのコード内 nfv = ∇α( )f ∇α( )f +δN 3/1 8 )/( 0.1 ∑ − = N i N NV e δ 解を安定化するもの (nfvが無限大になるのを防ぐ) 人工的に界面幅を圧縮する項 ffvf Snn ⋅= α場（赤:流体, 青:気体） α∇ interFoam (VOF法)
- 32. S-‐‑‒CLSVOF法 • ⽀支配⽅方程式 Navier-‐‑‒Stokes 式 流流体率率率αの移流流⽅方程式 ∂v ∂t +v⋅∇v= −∇P +ν∇2 v + Fσ + ρg :: liquid phase :: interface :: gas phase 1=α 0=α 10 <<α Level-‐Set関数 φ φ0 = (2α −1)⋅Γ Γ ; 無次元数 Γ = 0.75Δx Δx ; 無次元数 ∂φ ∂τ = S(φ0 ) 1− ∇φ( ) φ x,0( )= φ0 x( ) Re-‐iniYalizaYon equaYon ∂α ∂t + ∇⋅ αv( )= 0 ∇φ 反復回数φcorr φcorr = ε Δτ ε =1.5Δx 界面幅ε ρ =αρl +(1−α)ρg µ =αµl +(1−α)µg α∇ イメージ
- 33. S-‐‑‒CLSVOF法 • ⽀支配⽅方程式 Navier-‐‑‒Stokes 式 流流体率率率αの移流流⽅方程式 ∂v ∂t +v⋅∇v= −∇P +ν∇2 v + Fσ + ρg :: liquid phase :: interface :: gas phase 1=α 0=α 10 <<α Fσ =σkδ∇φ CSFモデル k = −∇⋅nf = −∇⋅ ∇φ( )f ∇φ( )f +δN $ % & & ' ( ) ) ∂α ∂t + ∇⋅ αv( )= 0 ダイラック関数δ δ φ( )= 0 δ φ( )= 1 2ε 1+cos πφ ε ! " # $ % & ! " # $ % & φ >ε φ ≤ε ヘビサイド関数H H φ( )= 0 H φ( )= 1 2 1+ φ ε + 1 π sin πφ ε ! " # $ % & ! " # $ % & H φ( )=1 曲率 ρ =αρl +(1−α)ρg µ =αµl +(1−α)µg
- 34. S-‐‑‒CLSVOF法 • ⽀支配⽅方程式 Navier-‐‑‒Stokes 式 流流体率率率αの移流流⽅方程式 ∂v ∂t +v⋅∇v= −∇P +ν∇2 v + Fσ + ρg :: liquid phase :: interface :: gas phase 1=α 0=α 10 <<α ∂α ∂t + ∇⋅ αv( )= 0 ヘビサイド関数H H φ( )= 0 H φ( )= 1 2 1+ φ ε + 1 π sin πφ ε ! " # $ % & ! " # $ % & H φ( )=1 ρ =αρl +(1−α)ρg µ =αµl +(1−α)µg ρ = Hρl +(1− H)ρg µ = Hµl +(1− H)µg 一般には物性値をヘビサイド関数で更新 しかし、A. Albadawi et al. (2013)では 物性値はヘビサイド関数で更新せず φ < −ε φ ≤ ε φ > ε
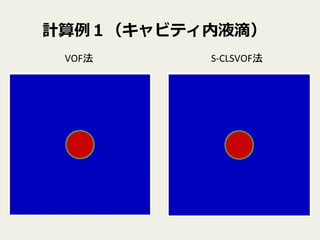
- 35. 計算例例１（キャビティ内液滴） 0.1 m 0.1 m 0.5 m/s 0.02 m liquid 1 liquid 2 物性値 動粘度 1.0 x 10-‐3 m2/s 表面張力 10 mN/m 目的 剪断によって液滴がどのように変形するか （浮力差による影響は無視するため物性は liquid 1とliquid 2で同じで表面張力のみ発生 するという系） 計算１ interFoam (VOF法) 計算２ sclsVOFFoam(S-‐CLSVOF法) 計算格子 200 x 200 (x, y direcYon) x y
- 36.
- 37.
- 38. 計算例例2（ダムブレイク） 0.584 m 0.584 m 0.048 m 0.292 m 0.292 m 0.1461 m phase 1 動粘度 1 x 10-‐6 m2/s 密度 1000 kg/m3 phase 1 phase 2 phase 2 動粘度 1.48 x 10-‐5 m2/s 密度 1 kg/m3 表面張力 70 mN/m
- 39.
- 40. 計算例例2（ダムブレイク） VOF法 S-‐CLSVOF法 0.2 s 0.2 s 0.3 s 0.3 s 0.4 s 0.4 s 0.5 s 0.5 s