Download as PDF, PPTX
![曲げ配管の流れの最適化
2014/3/8 第28回オープンＣＡＥ勉強会@関西 7
目的関数
ソルバ ：simpleFoam
動粘度 ：1.5e-05 [m2/s2]
乱流モデル ：kOmegaSST outlet
U: pressureInletOutletVelocity
p : totalPressure p0=0
inlet
U:fixedValue (0 0 10)
p:zeroGradient
Objective Function 3
pipe Length
Objective Function 1
inlet pressure average
Objective Function 2
outlet velocity sum of squares
目的関数１,2,3を最小化する](https://image.slidesharecdn.com/optimizationflowchannelgeometry14030828th-140618084302-phpapp02/75/OpenFOAM-OpenMDAO-28-CAE-7-2048.jpg)
配管流路の多目的最適化OpenFOAM+OpenMDAO(第28回オープンCAE勉強会@関西)
- 1. 第28回オープンCAE勉強会@ 関西 2014. 03.08 片山達也 配管流路の多目的最適化 OpenFOAM + OpenMDAO
- 2. 目次 2014/3/8 第28回オープンＣＡＥ勉強会@関西 2 多目的最適化 曲げ配管の流れ最適化 最適化問題 解析の自動化 応答曲面の作成(Krigingモデル) 多目的最適化(NSGA2) 自己組織化マップ(SOM) 付録
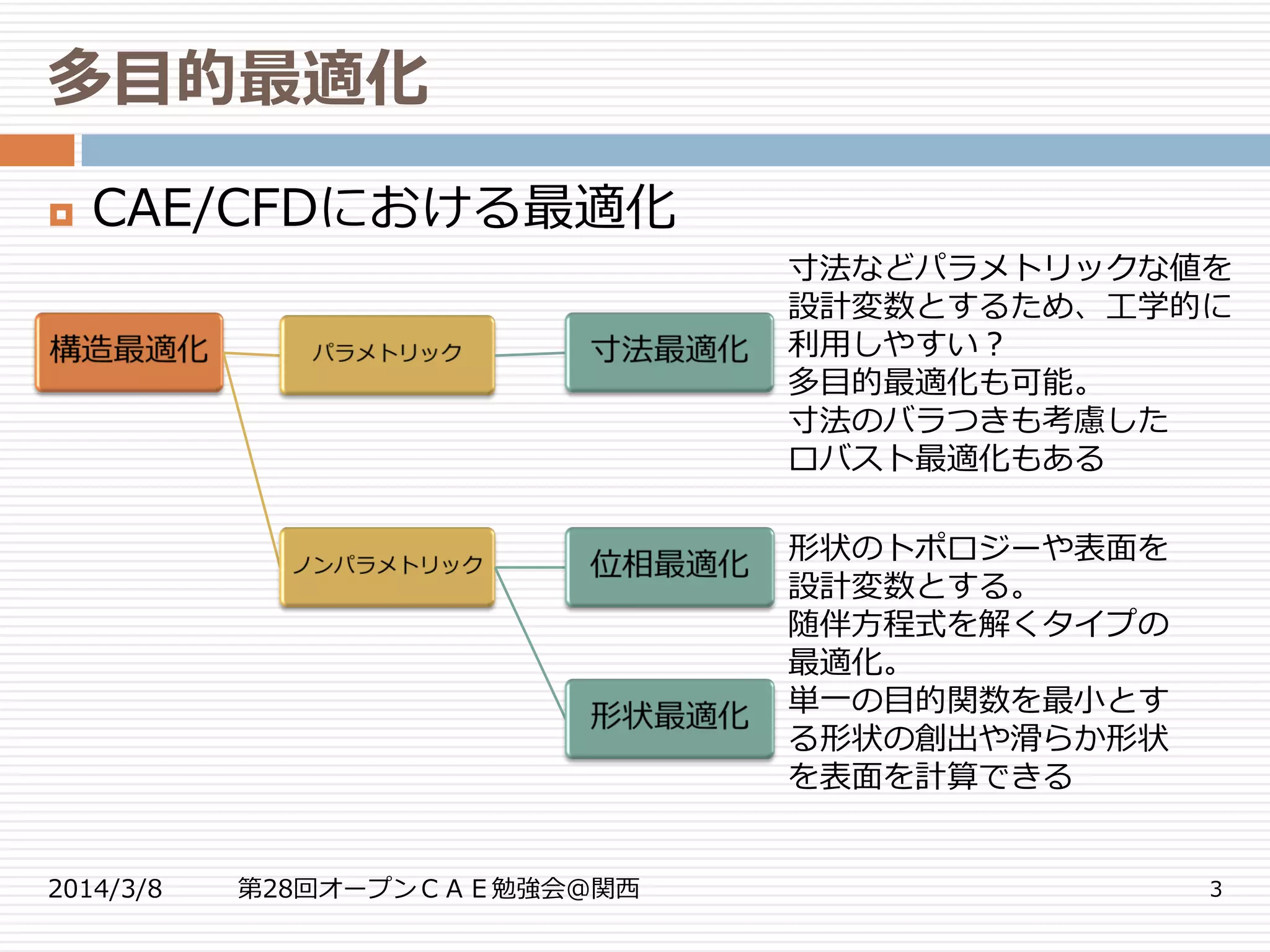
- 3. 多目的最適化 2014/3/8 第28回オープンＣＡＥ勉強会@関西 3 CAE/CFDにおける最適化 寸法などパラメトリックな値を 設計変数とするため、工学的に 利用しやすい？ 多目的最適化も可能。 寸法のバラつきも考慮した ロバスト最適化もある 形状のトポロジーや表面を 設計変数とする。 随伴方程式を解くタイプの 最適化。 単一の目的関数を最小とす る形状の創出や滑らか形状 を表面を計算できる
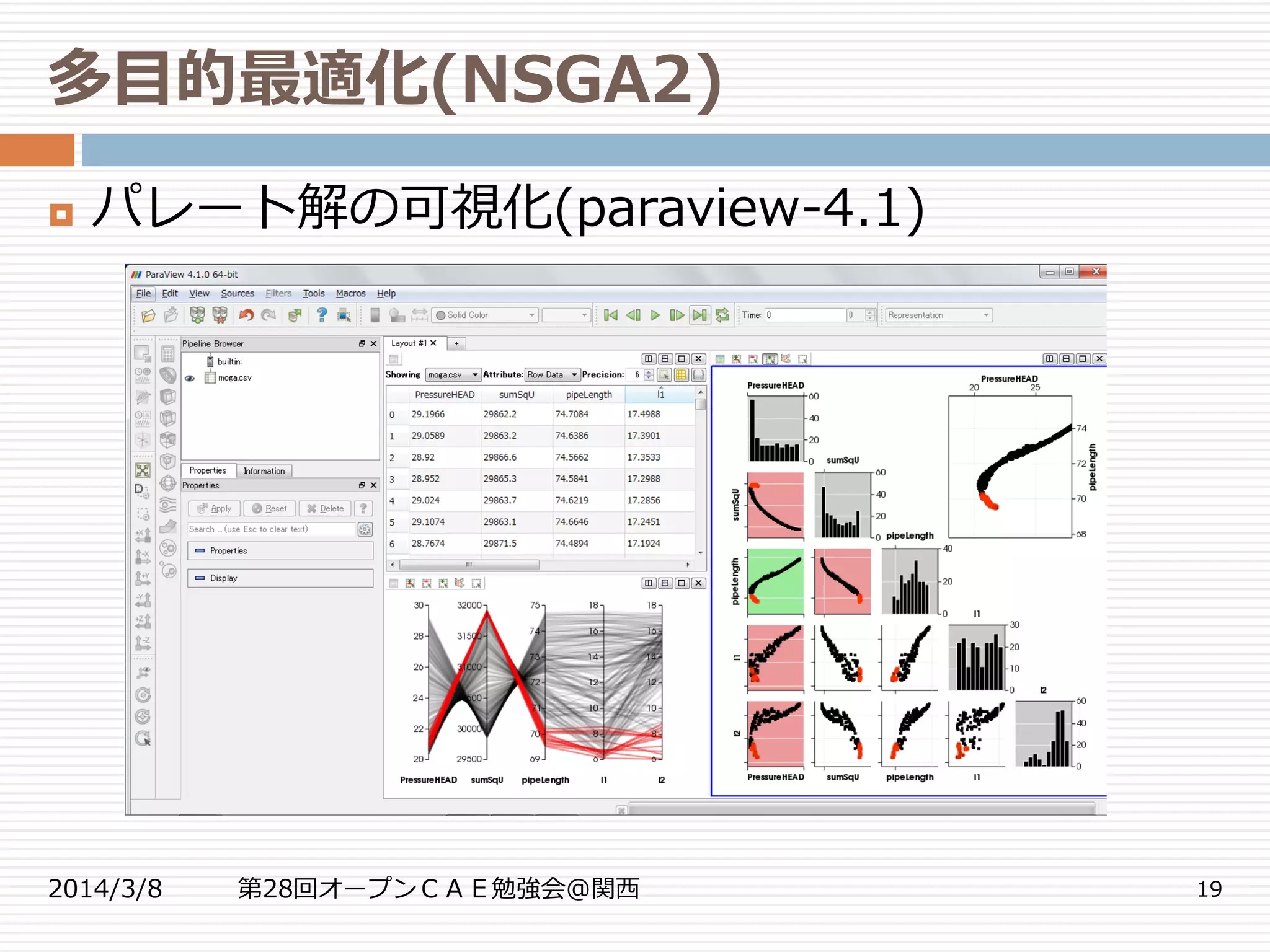
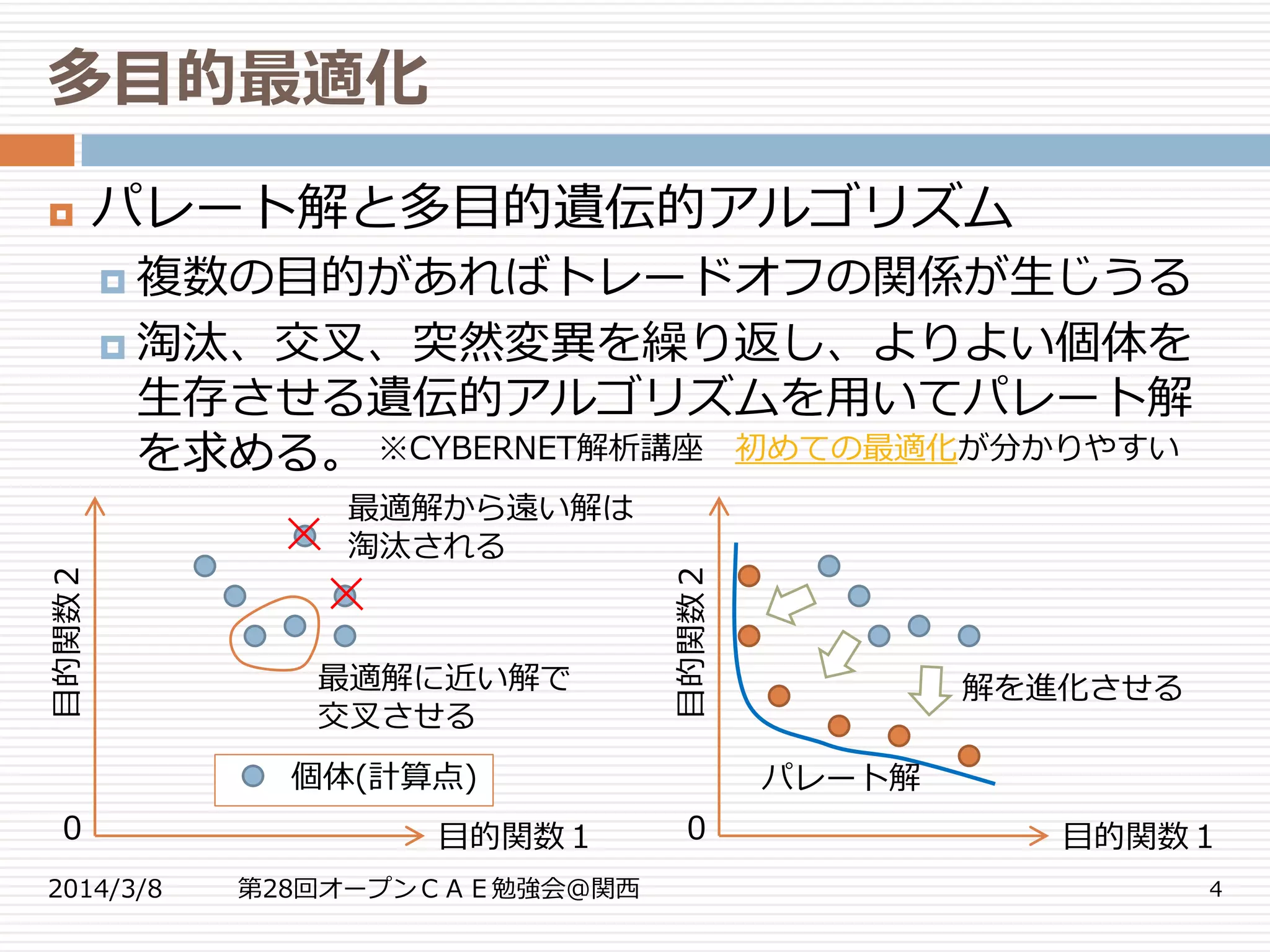
- 4. 多目的最適化 2014/3/8 第28回オープンＣＡＥ勉強会@関西 4 パレート解と多目的遺伝的アルゴリズム 複数の目的があればトレードオフの関係が生じうる 淘汰、交叉、突然変異を繰り返し、よりよい個体を 生存させる遺伝的アルゴリズムを用いてパレート解 を求める。 ※CYBERNET解析講座 初めての最適化が分かりやすい 0 個体(計算点) 目的関数１ 目的関数２ 最適解から遠い解は 淘汰される 最適解に近い解で 交叉させる 0 目的関数１ 目的関数２ 解を進化させる パレート解
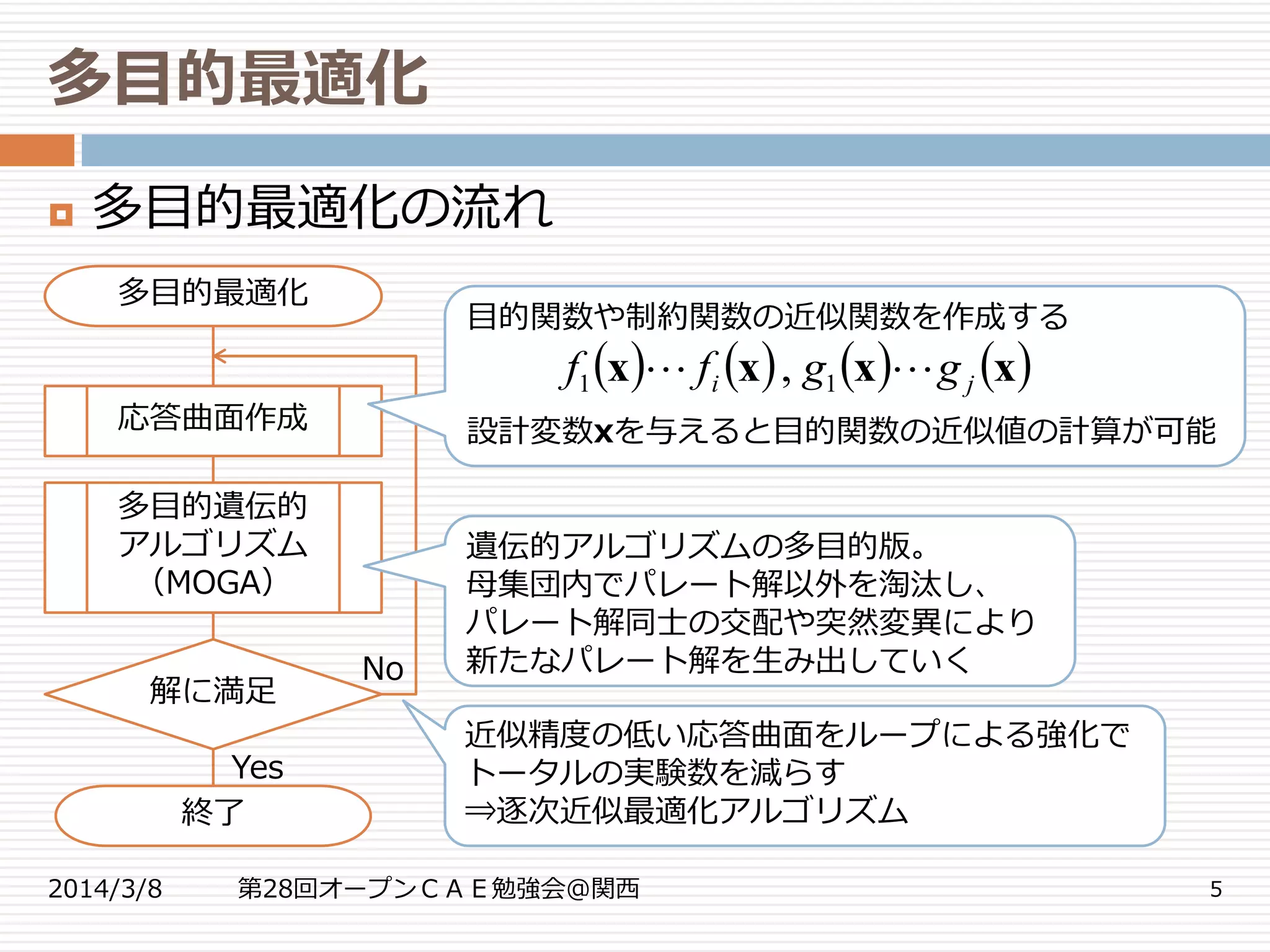
- 5. 多目的最適化 2014/3/8 第28回オープンＣＡＥ勉強会@関西 5 多目的最適化の流れ 解に満足 多目的最適化 終了 応答曲面作成 多目的遺伝的 アルゴリズム （MOGA） Yes No 目的関数や制約関数の近似関数を作成する 設計変数xを与えると目的関数の近似値の計算が可能 xxxx ji ggff 11 , 遺伝的アルゴリズムの多目的版。 母集団内でパレート解以外を淘汰し、 パレート解同士の交配や突然変異により 新たなパレート解を生み出していく 近似精度の低い応答曲面をループによる強化で トータルの実験数を減らす ⇒逐次近似最適化アルゴリズム
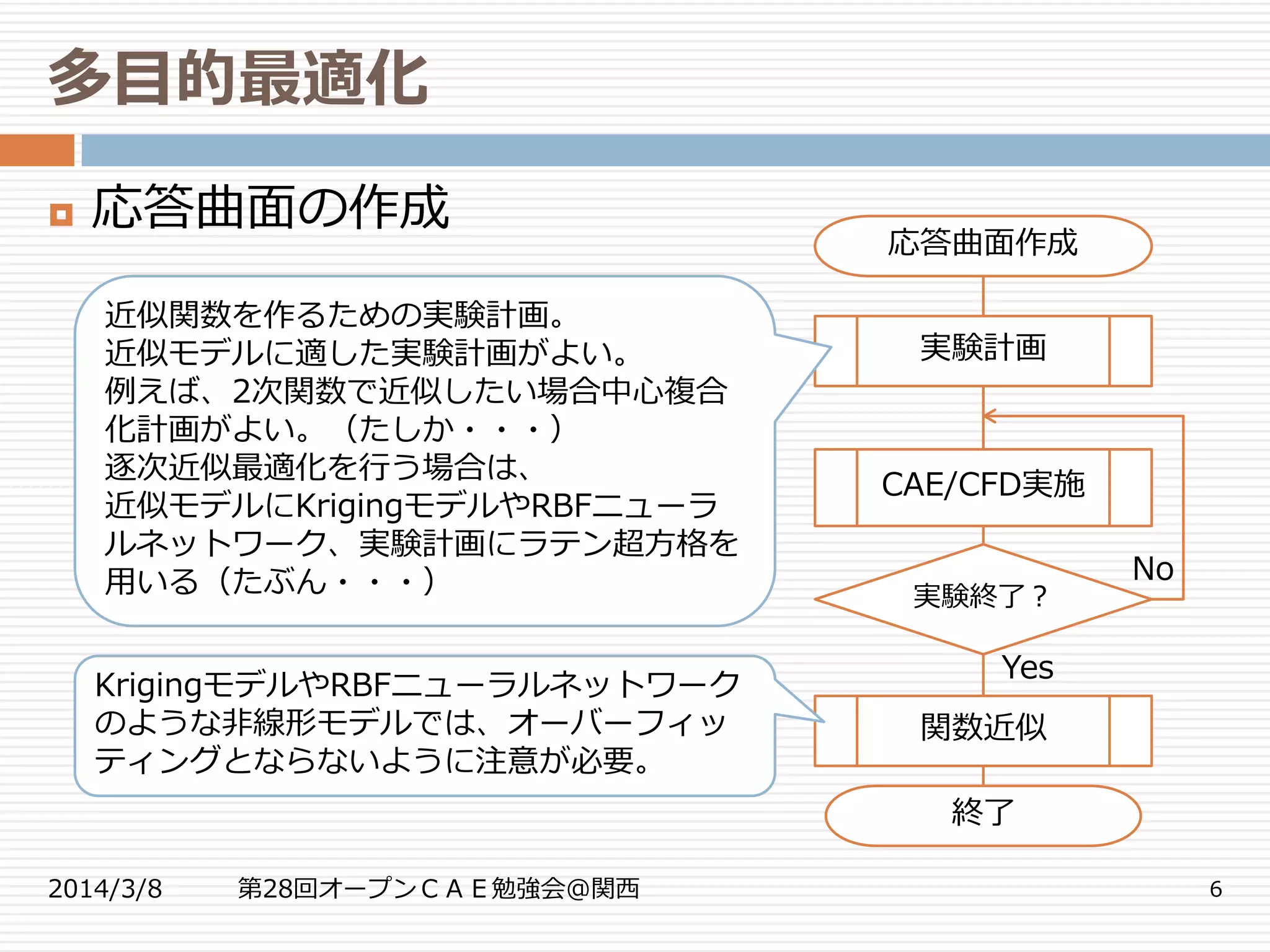
- 6. 多目的最適化 2014/3/8 第28回オープンＣＡＥ勉強会@関西 6 応答曲面の作成 実験終了？ 応答曲面作成 終了 実験計画 CAE/CFD実施 Yes No 関数近似 近似関数を作るための実験計画。 近似モデルに適した実験計画がよい。 例えば、2次関数で近似したい場合中心複合 化計画がよい。（たしか・・・） 逐次近似最適化を行う場合は、 近似モデルにKrigingモデルやRBFニューラ ルネットワーク、実験計画にラテン超方格を 用いる（たぶん・・・） KrigingモデルやRBFニューラルネットワーク のような非線形モデルでは、オーバーフィッ ティングとならないように注意が必要。
- 7. 曲げ配管の流れの最適化 2014/3/8 第28回オープンＣＡＥ勉強会@関西 7 目的関数 ソルバ ：simpleFoam 動粘度 ：1.5e-05 [m2/s2] 乱流モデル ：kOmegaSST outlet U: pressureInletOutletVelocity p : totalPressure p0=0 inlet U:fixedValue (0 0 10) p:zeroGradient Objective Function 3 pipe Length Objective Function 1 inlet pressure average Objective Function 2 outlet velocity sum of squares 目的関数１,2,3を最小化する
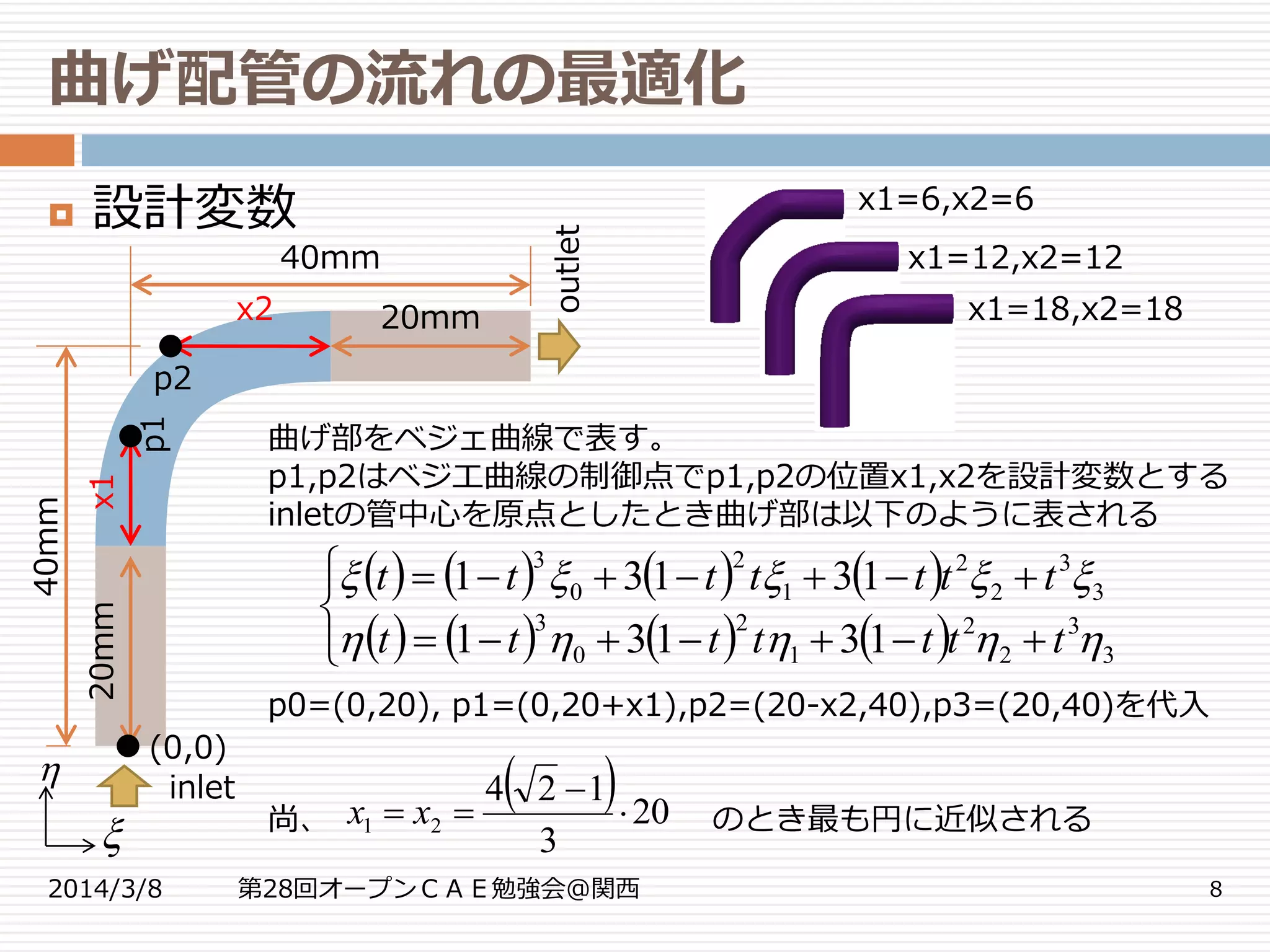
- 8. 曲げ配管の流れの最適化 2014/3/8 第28回オープンＣＡＥ勉強会@関西 8 設計変数 曲げ部をベジェ曲線で表す。 p1,p2はベジエ曲線の制御点でp1,p2の位置x1,x2を設計変数とする inletの管中心を原点としたとき曲げ部は以下のように表される p0=(0,20), p1=(0,20+x1),p2=(20-x2,40),p3=(20,40)を代入 尚、 のとき最も円に近似される 40mm 20mm 20mm 40mm x2 x1 p2 p1 inlet outlet (0,0) x1=6,x2=6 x1=12,x2=12 x1=18,x2=18 3 3 2 2 1 2 0 3 3 3 2 2 1 2 0 3 13131 13131 ttttttt ttttttt 20 3 124 21 xx
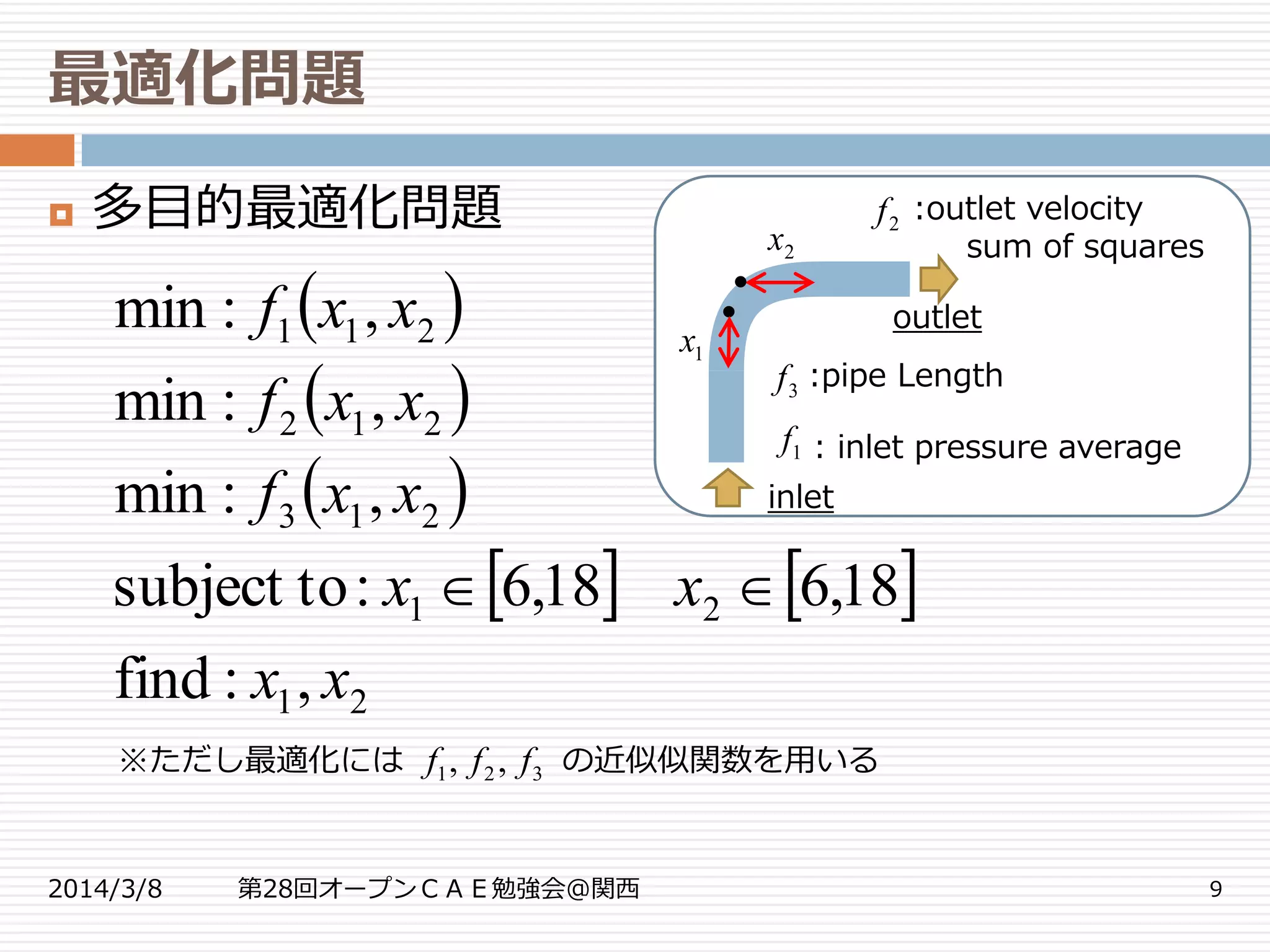
- 9. 最適化問題 2014/3/8 第28回オープンＣＡＥ勉強会@関西 9 多目的最適化問題 21 21 213 212 211 ,:find 18,618,6:tosubject ,:min ,:min ,:min xx xx xxf xxf xxf outlet inlet : inlet pressure average :outlet velocity sum of squares 1f 3f 2f :pipe Length 2x 1x ※ただし最適化には の近似似関数を用いる321 ,, fff
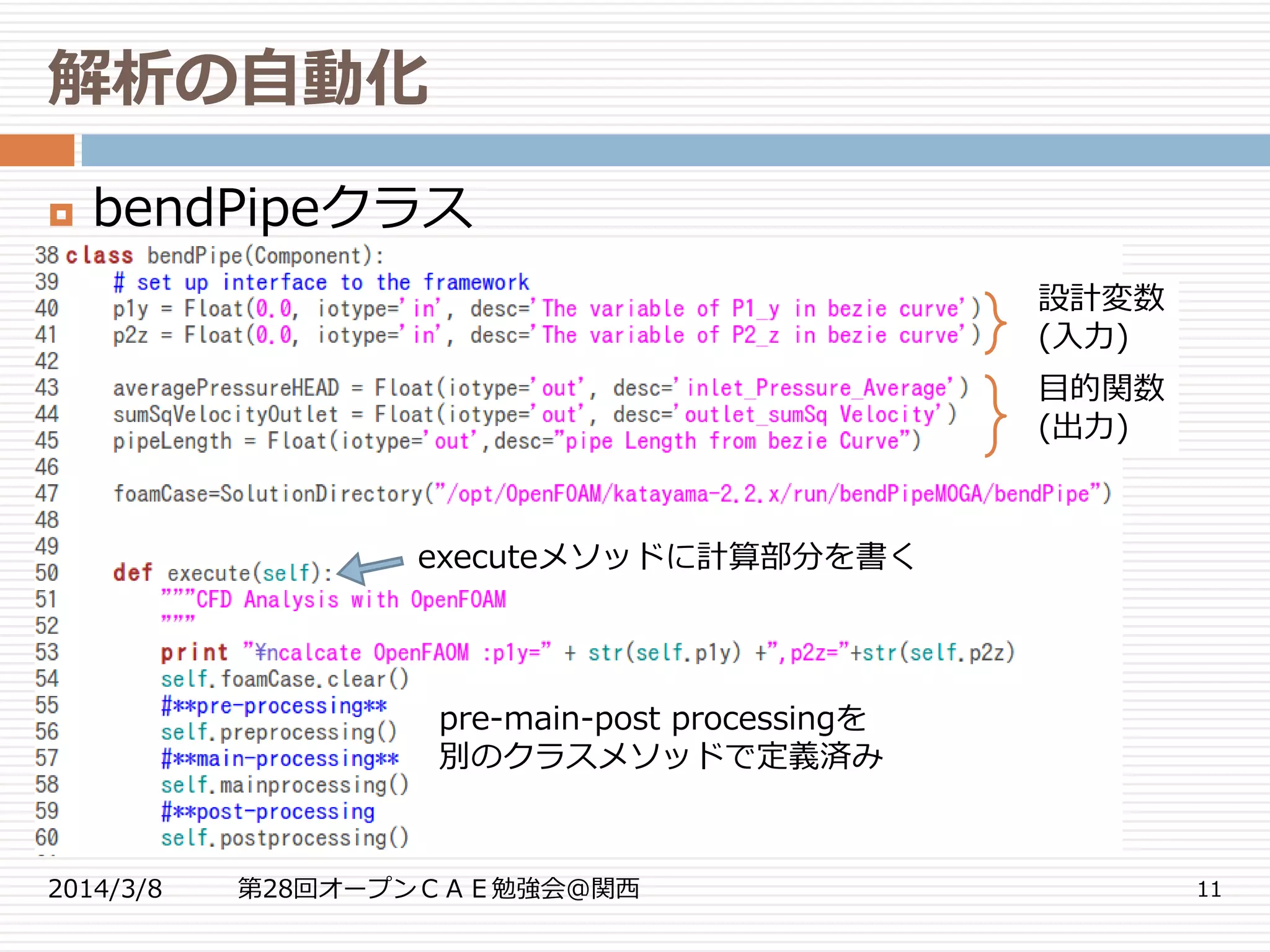
- 10. 解析の自動化 2014/3/8 第28回オープンＣＡＥ勉強会@関西 10 Componentクラス OpenMDAOでは計算部分をComponentクラスを継 承して記述する必要がある input-outputとなるクラス変数、計算を実行するク ラスメソッドexecute()を定義する execute内で、iotype=outのクラス変数に値を入力 する インスタンス生成後、iotype=inのクラス変数に値を 入力し、クラスメソッドexecute()を実行すれば計算 が行われ、iotype=outのクラス変数に値が入る
- 11. 解析の自動化 2014/3/8 第28回オープンＣＡＥ勉強会@関西 11 bendPipeクラス 設計変数 (入力) 目的関数 (出力) executeメソッドに計算部分を書く pre-main-post processingを 別のクラスメソッドで定義済み
- 12. 解析の自動化 2014/3/8 第28回オープンＣＡＥ勉強会@関西 12 クラスメソッド：preprocessing() 1. blockMesh内曲げ部のedgeをspline定義 2. ベジエ曲線からedgeのsplineを計算 3. pyFoamを用いてblockMeshDictを編集 4. blockMeshの実行 クラスメソッド： mainprocessing() 1. simpleFoamの実行 ※１ ※2 ※2 ※1 PyFoam.RunDictionary.ParsedBlockMeshDict.ParsedBlockMeshDictを利用 ※2 PyFoam.Execution.BasicRunner.BasicRunnerを利用
- 13. 解析の自動化 2014/3/8 第28回オープンＣＡＥ勉強会@関西 13 クラスメソッド： postprocessing() 1. functionObjectを用いinlet Pressure Averageを ログ出力。pyFoamを用いてログ解析 2. 最終timeStepのUを読み込み( )、 outlet velocity sum of squaresを計算 3. pipe Lengthについてはpreprocessingにて取得 ※3 ※1 PyFoam.RunDictionary.ParsedBlockMeshDict.ParsedBlockMeshDictを利用 ※2 PyFoam.Execution.BasicRunner.BasicRunnerを利用 ※２
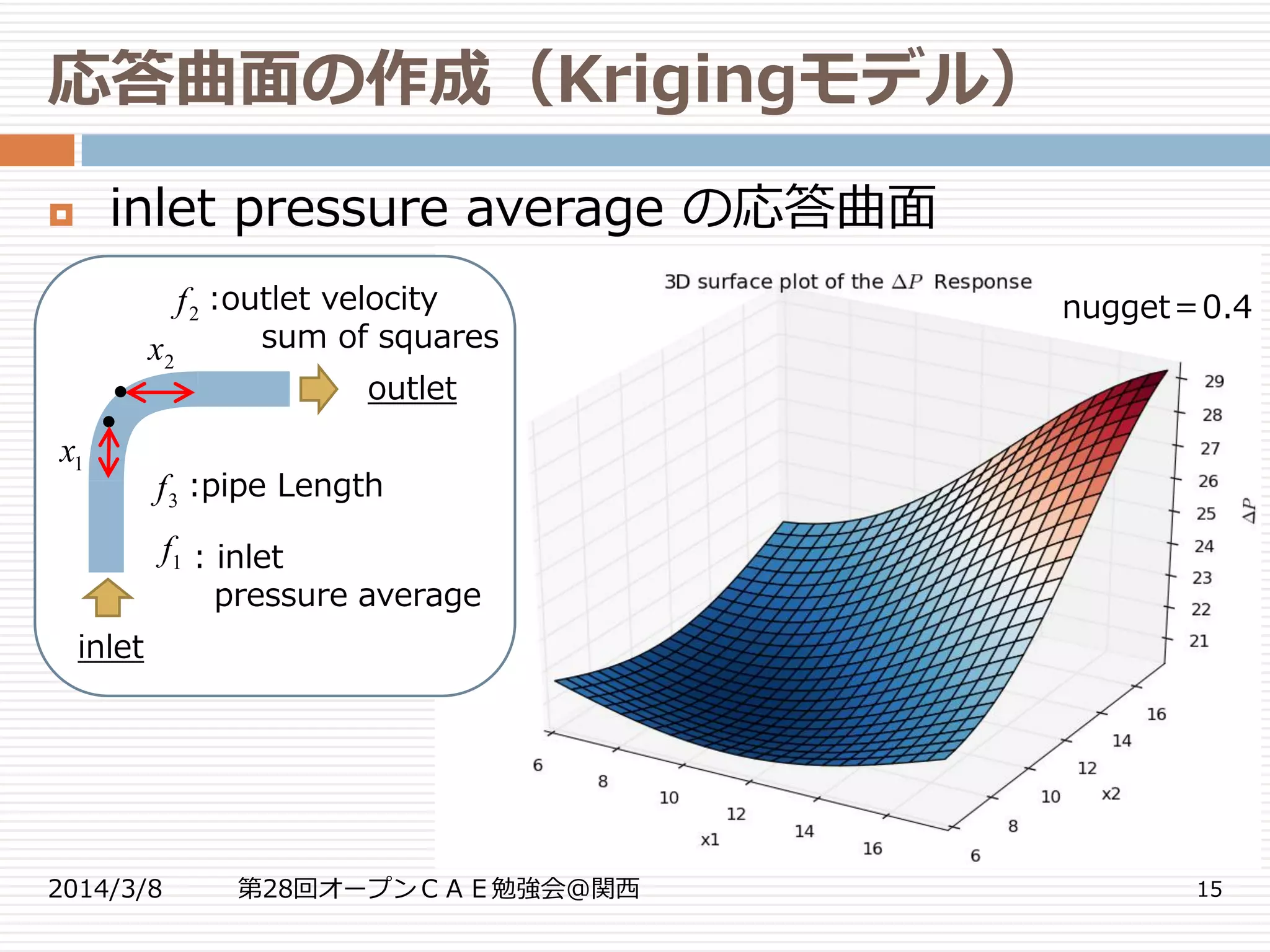
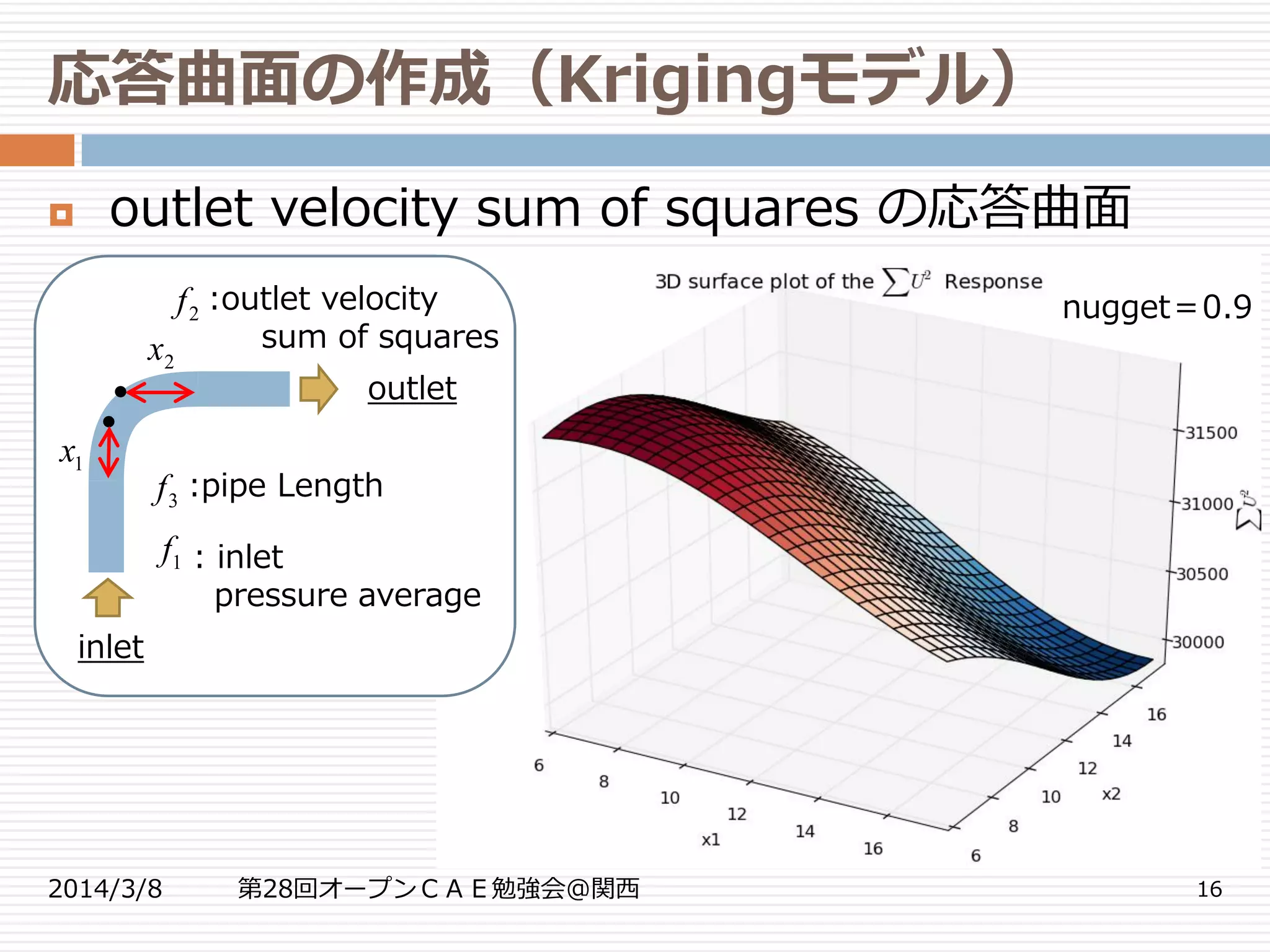
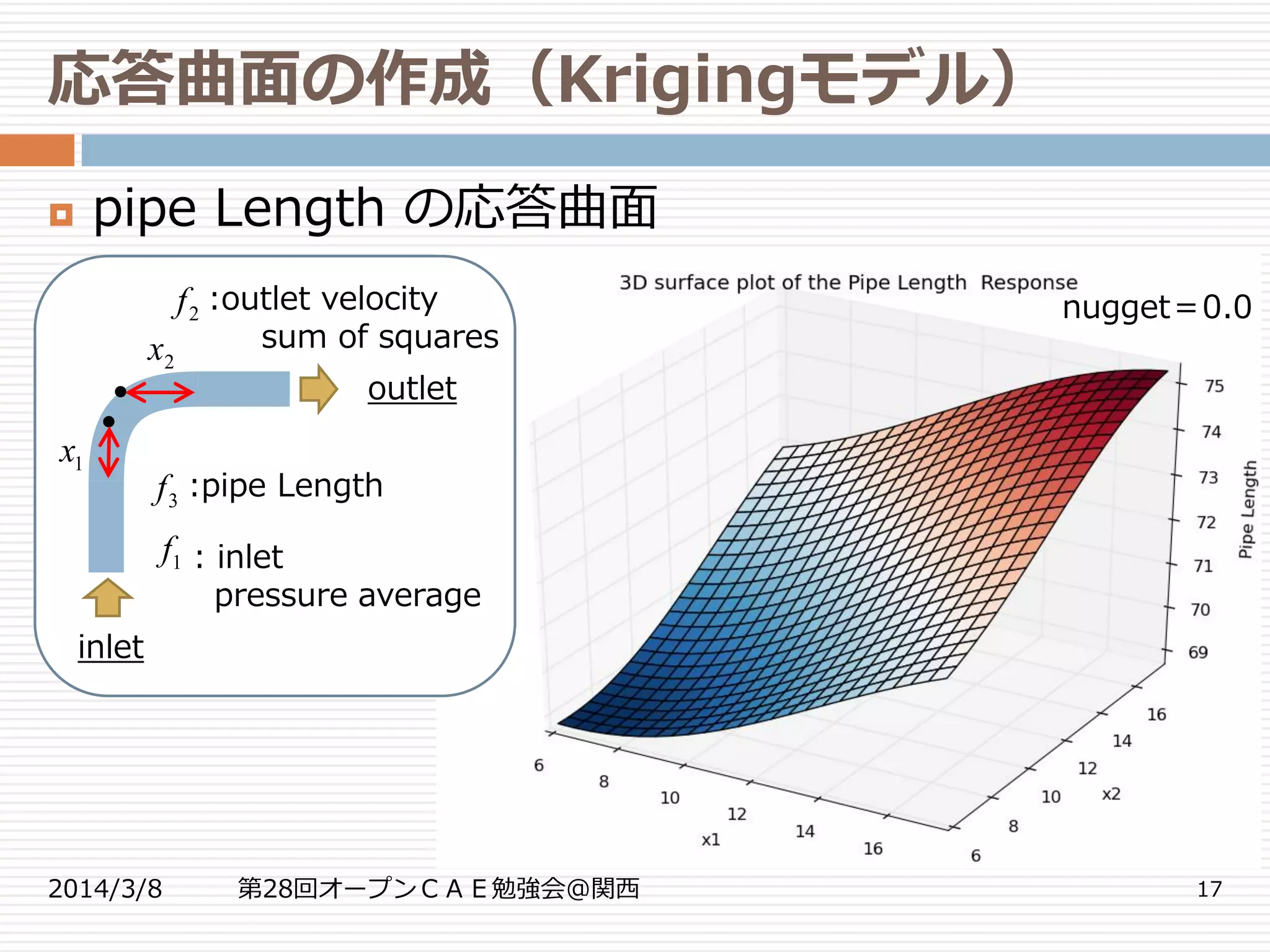
- 14. 応答曲面の作成（Krigingモデル） 2014/3/8 第28回オープンＣＡＥ勉強会@関西 14 実験計画 ２変数について各５水準の計５2回実験する メタモデル(近似関数) 近似関数 Pressure Average の近似モデル：Kriging nugget(平滑化パラメータ)の使用 outlet velocity sum of squaresの近似モデル：Kriging nugget(平滑化パラメータ)の使用 pipe Lengthの近似モデル：Kriging nugget(平滑化パラメータ)の使用 モデル bendPipeインスタンス
- 15. 応答曲面の作成（Krigingモデル） 2014/3/8 第28回オープンＣＡＥ勉強会@関西 15 inlet pressure average の応答曲面 nugget＝0.4 outlet inlet : inlet pressure average :outlet velocity sum of squares 1f 3f 2f :pipe Length 2x 1x
- 16. 応答曲面の作成（Krigingモデル） 2014/3/8 第28回オープンＣＡＥ勉強会@関西 16 outlet velocity sum of squares の応答曲面 nugget＝0.9 outlet inlet : inlet pressure average :outlet velocity sum of squares 1f 3f 2f :pipe Length 2x 1x
- 17. 応答曲面の作成（Krigingモデル） 2014/3/8 第28回オープンＣＡＥ勉強会@関西 17 pipe Length の応答曲面 nugget＝0.0 outlet inlet : inlet pressure average :outlet velocity sum of squares 1f 3f 2f :pipe Length 2x 1x
- 18. 多目的最適化(NSGA2) 2014/3/8 第28回オープンＣＡＥ勉強会@関西 18 NSGA2 特徴 高速優越ソート シェアリングの代用 エリート主義 Optimizer Options 母集団：２００ 世代数：１０ 詳細資料 同志社大学 理工学部 インテリジェント情報工学科 知 的システムデザイン研究室の資料 その他のオプションは pyOpt NSGA2の Optimizer Options参照
- 19. 多目的最適化(NSGA2) 2014/3/8 第28回オープンＣＡＥ勉強会@関西 19 パレート解の可視化(paraview-4.1)
- 20. 今後 2014/3/8 第28回オープンＣＡＥ勉強会@関西 20 OpenMDAOの展開 構造寸法最適化(Salome-Meca) ロバスト寸法最適化 ノンパラメトリック最適化 自己組織化マップ 逐次近似最適化 OpenMDAOをlibraryとして使う 並列化
- 21. 付録 2014/3/8 第28回オープンＣＡＥ勉強会@関西 21 使用ツール OpenFOAM (ver:2.2.x) blockMeshによる形状変更 simpleFoamによる解析 pyFoam (ver:0.6.1) python libraryとして使用しCFD解析を自動化 OpenMDAO (ver:0.9.2) 応答曲面作成(実験計画/近似モデル) 多目的最適化(NSGA2 @pyOpt (ver:1.1.0))