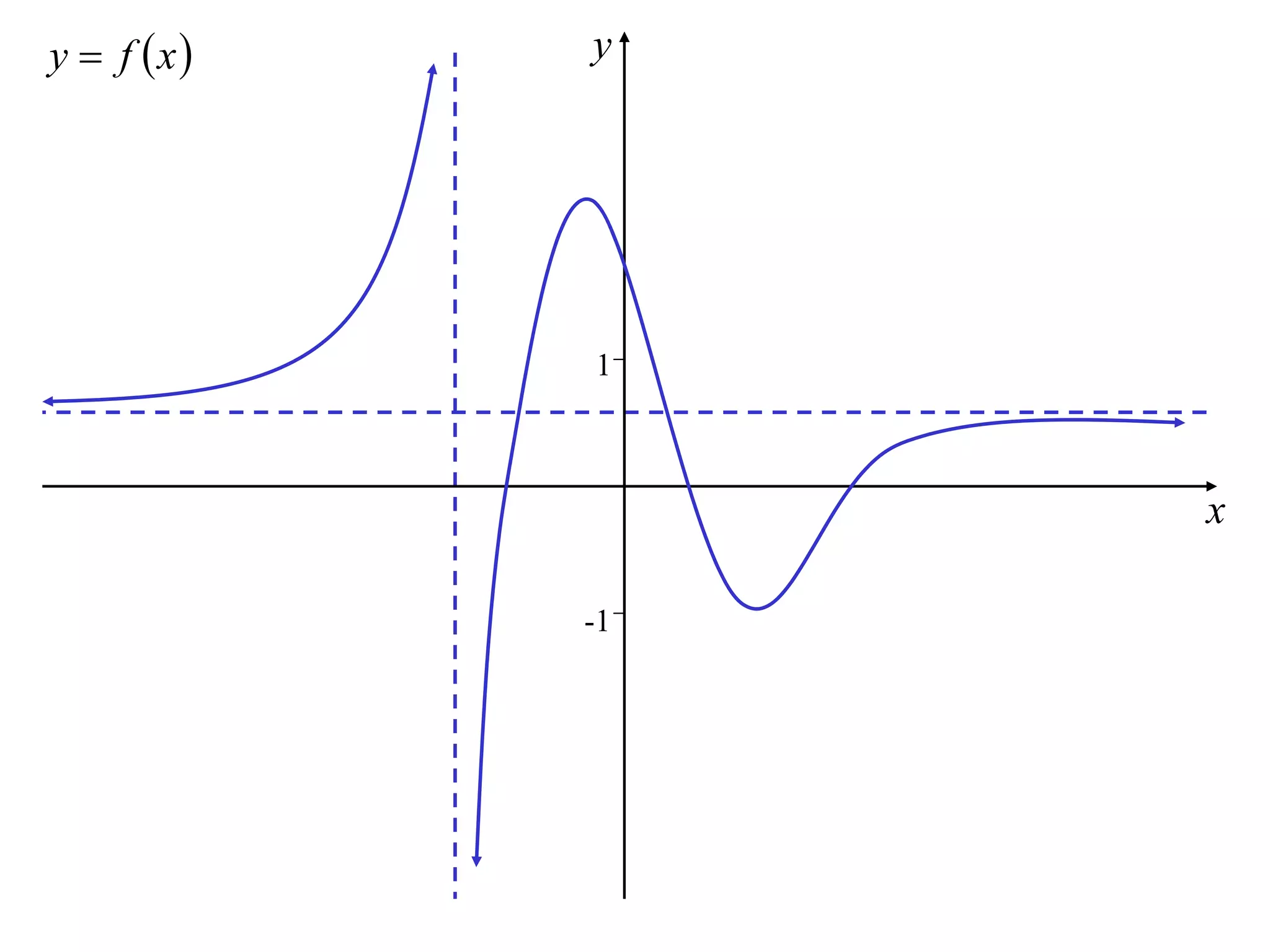
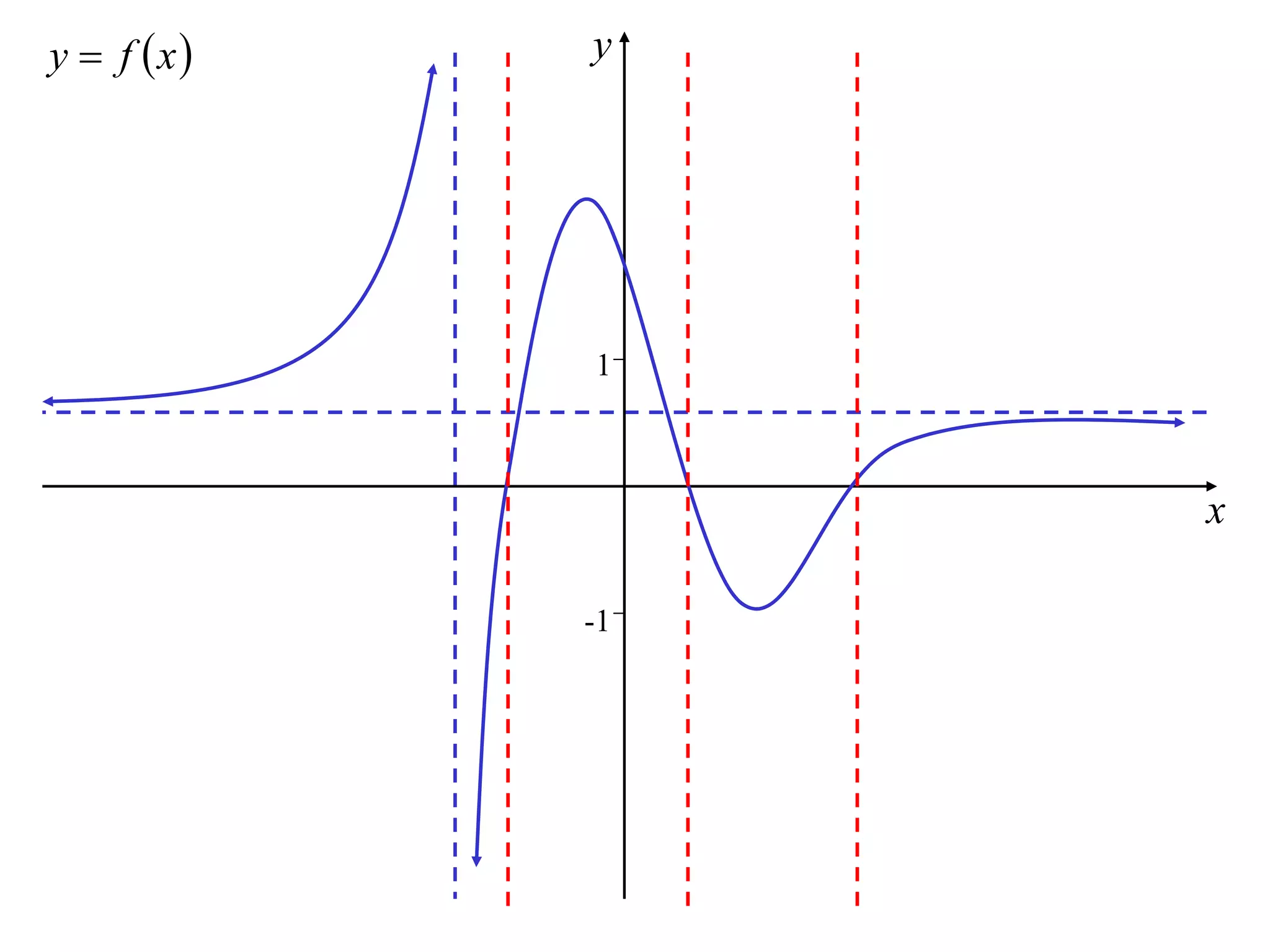
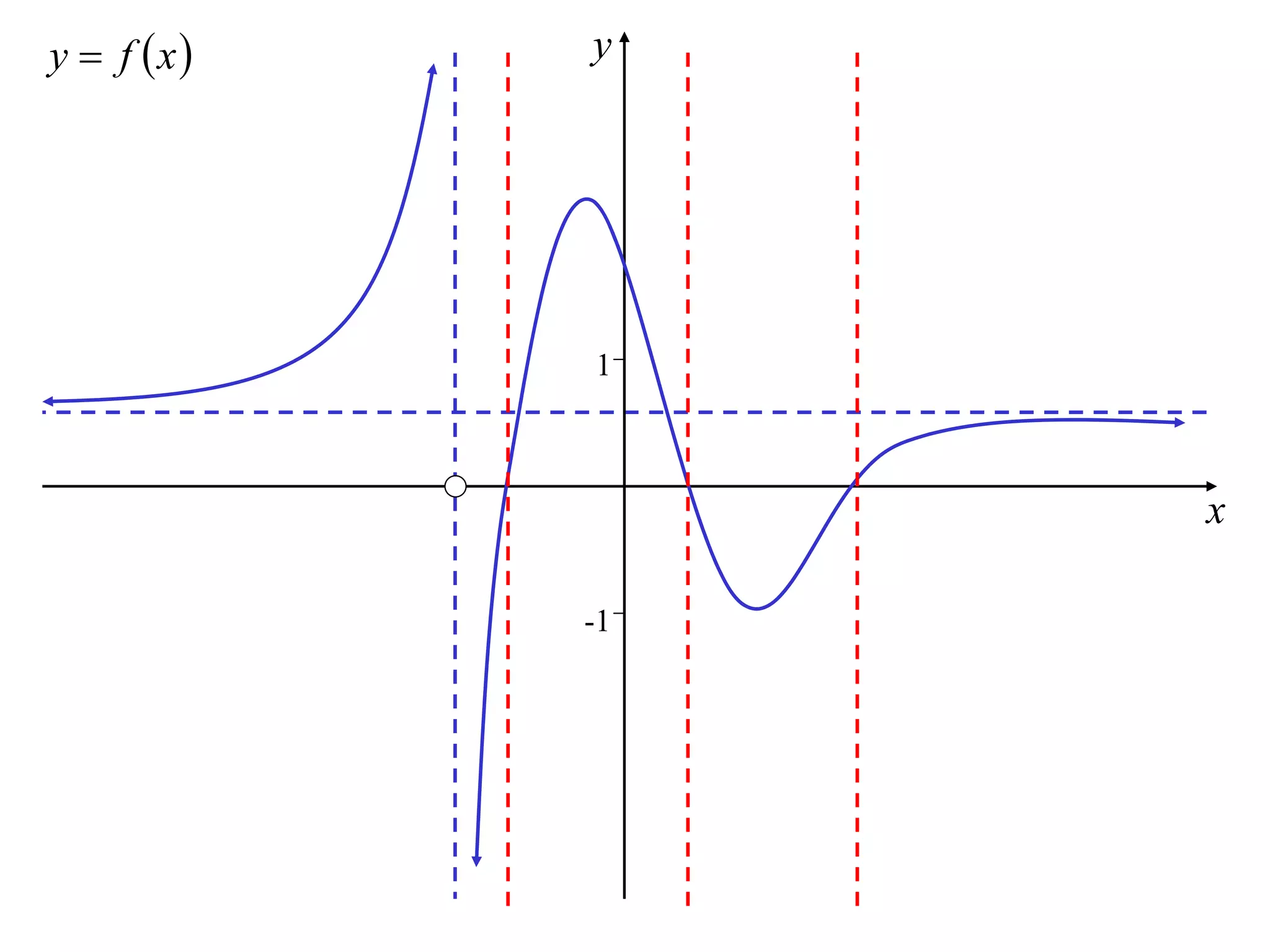
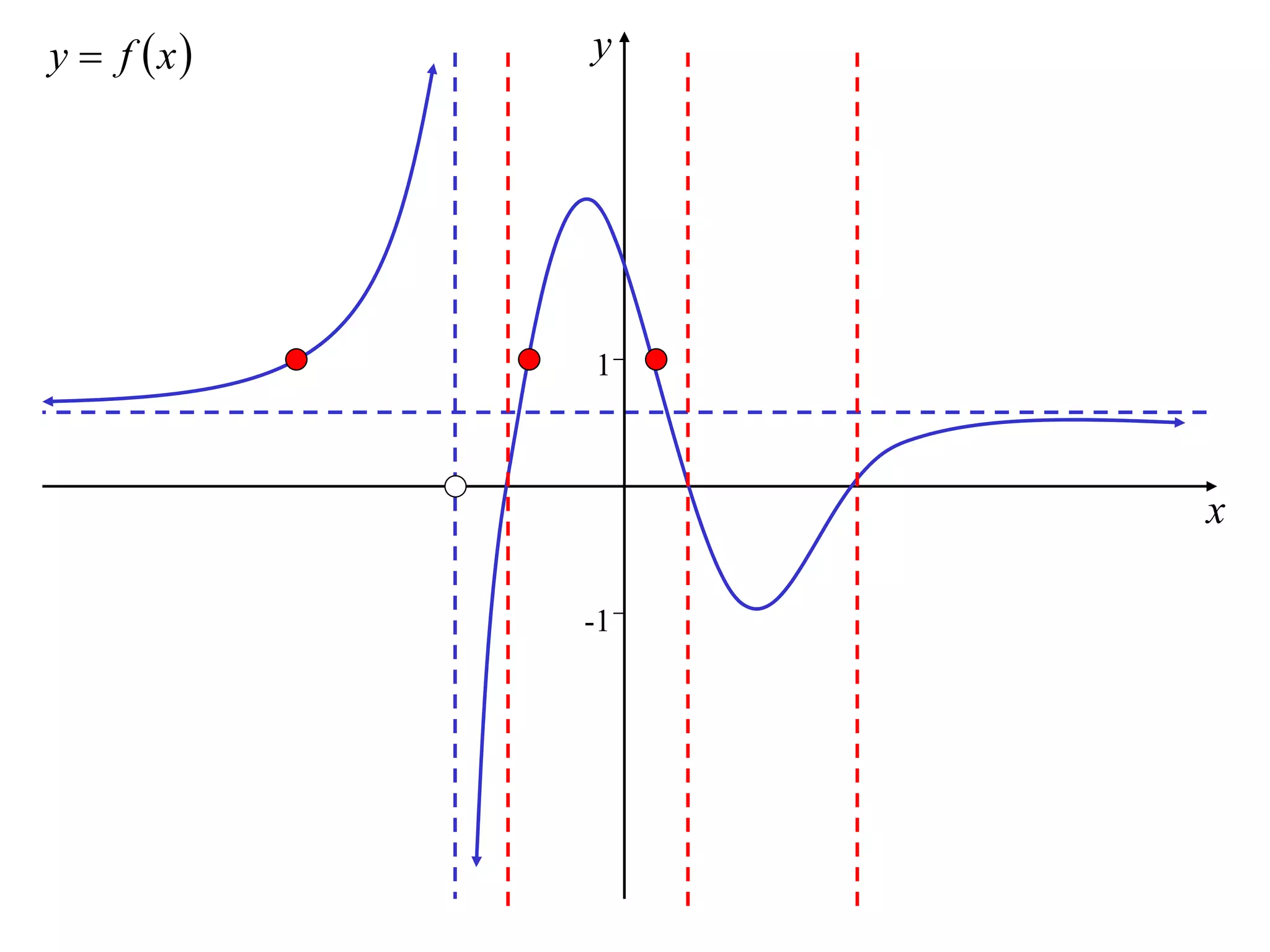
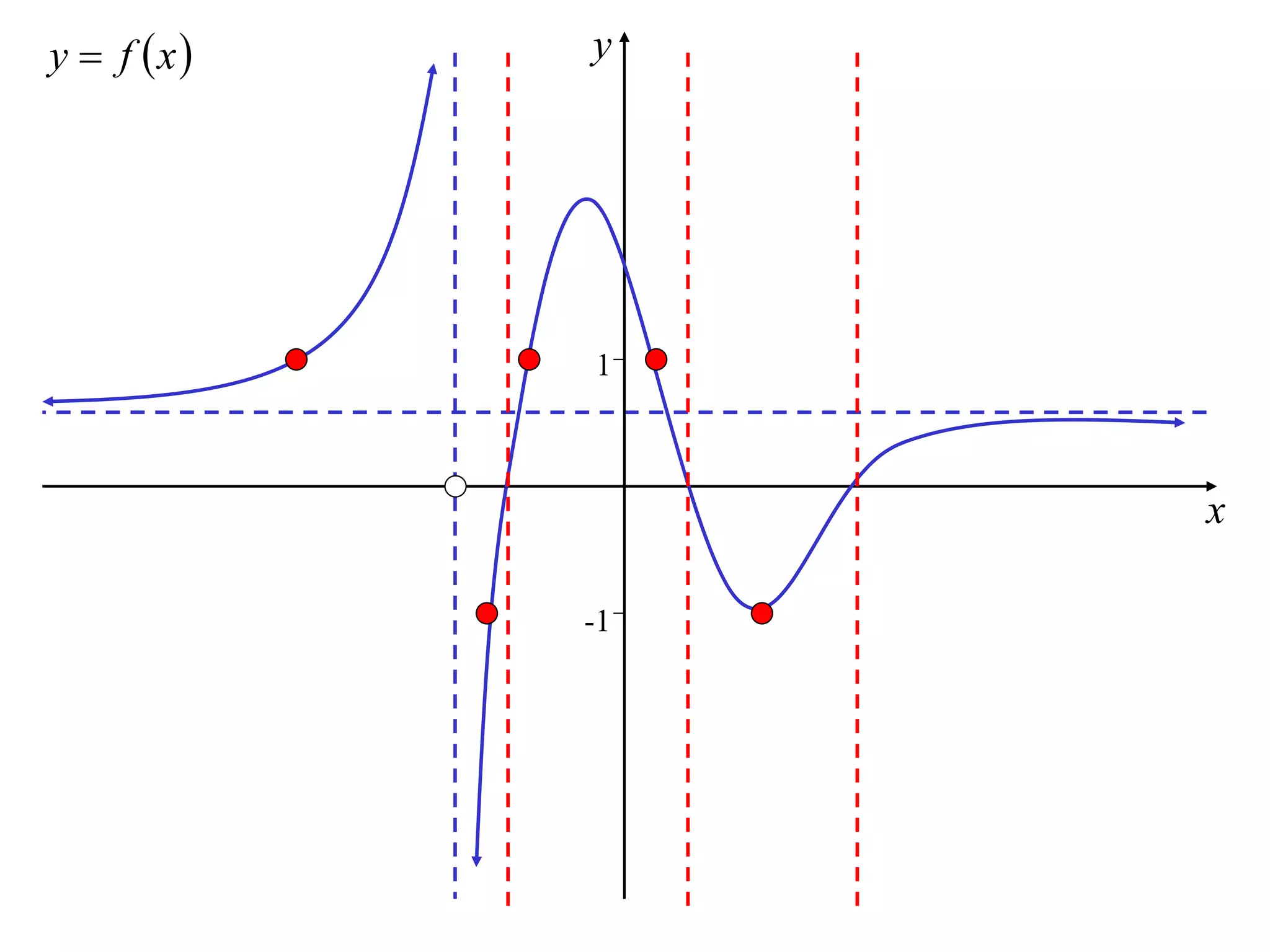
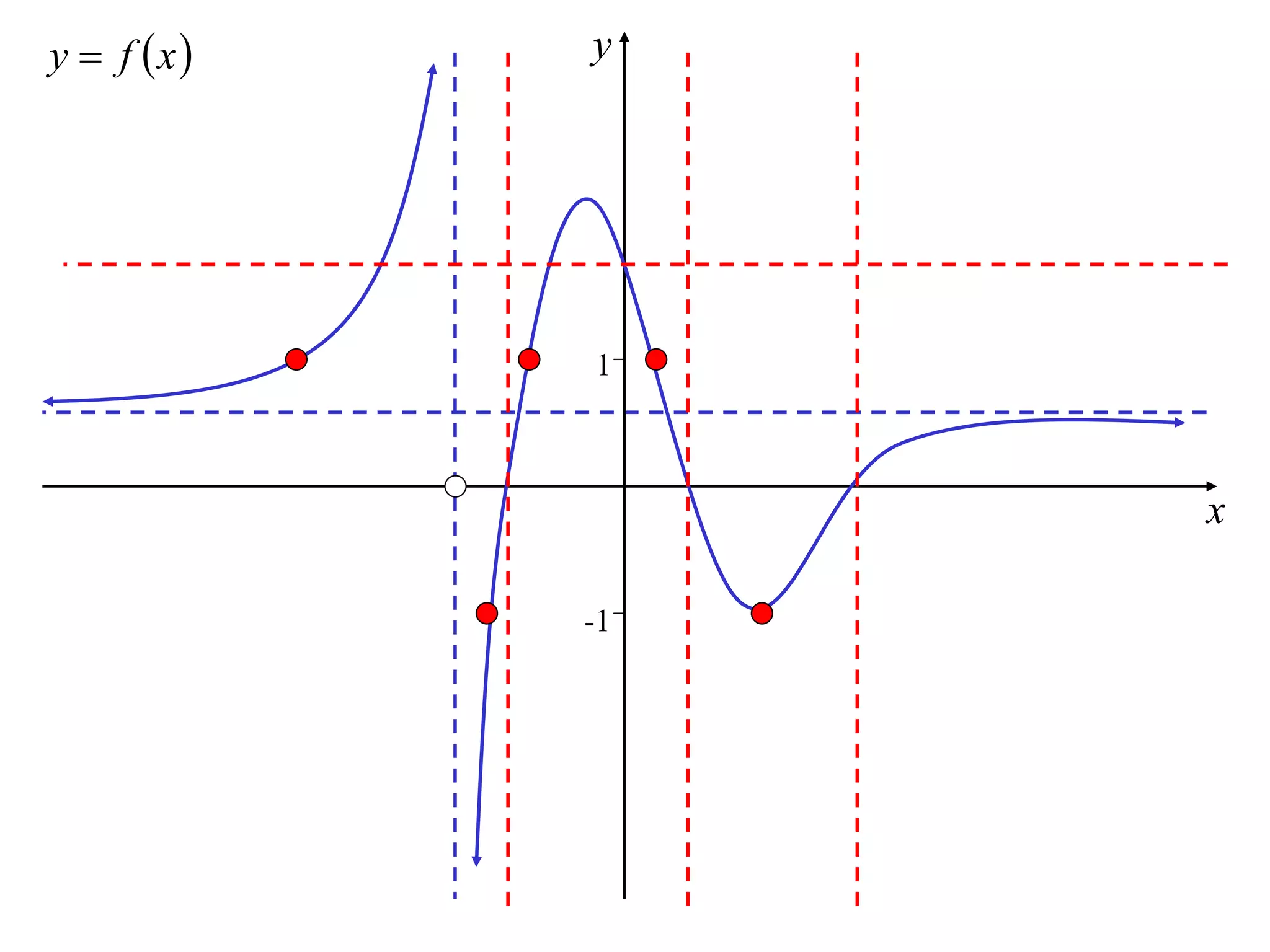
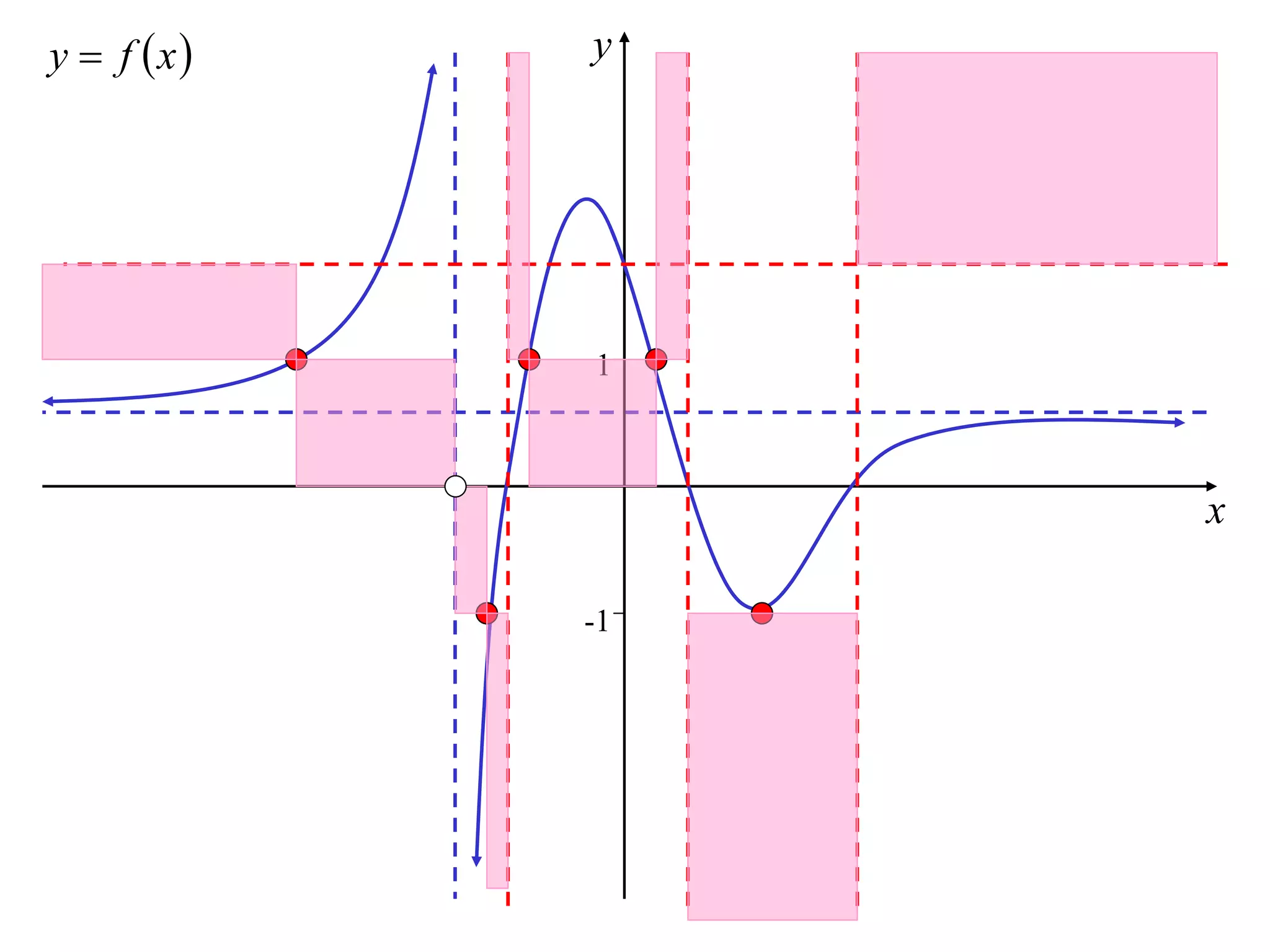
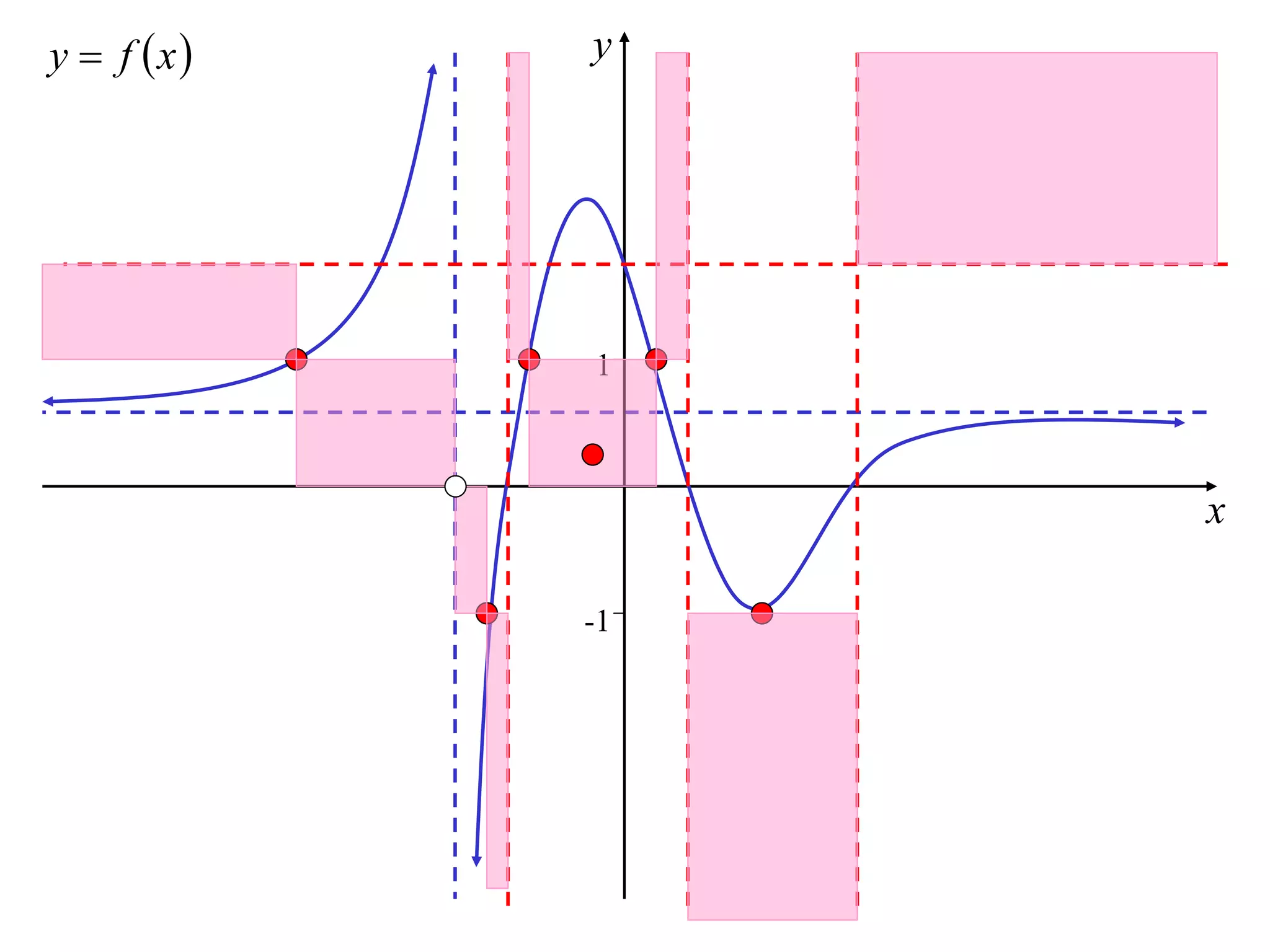
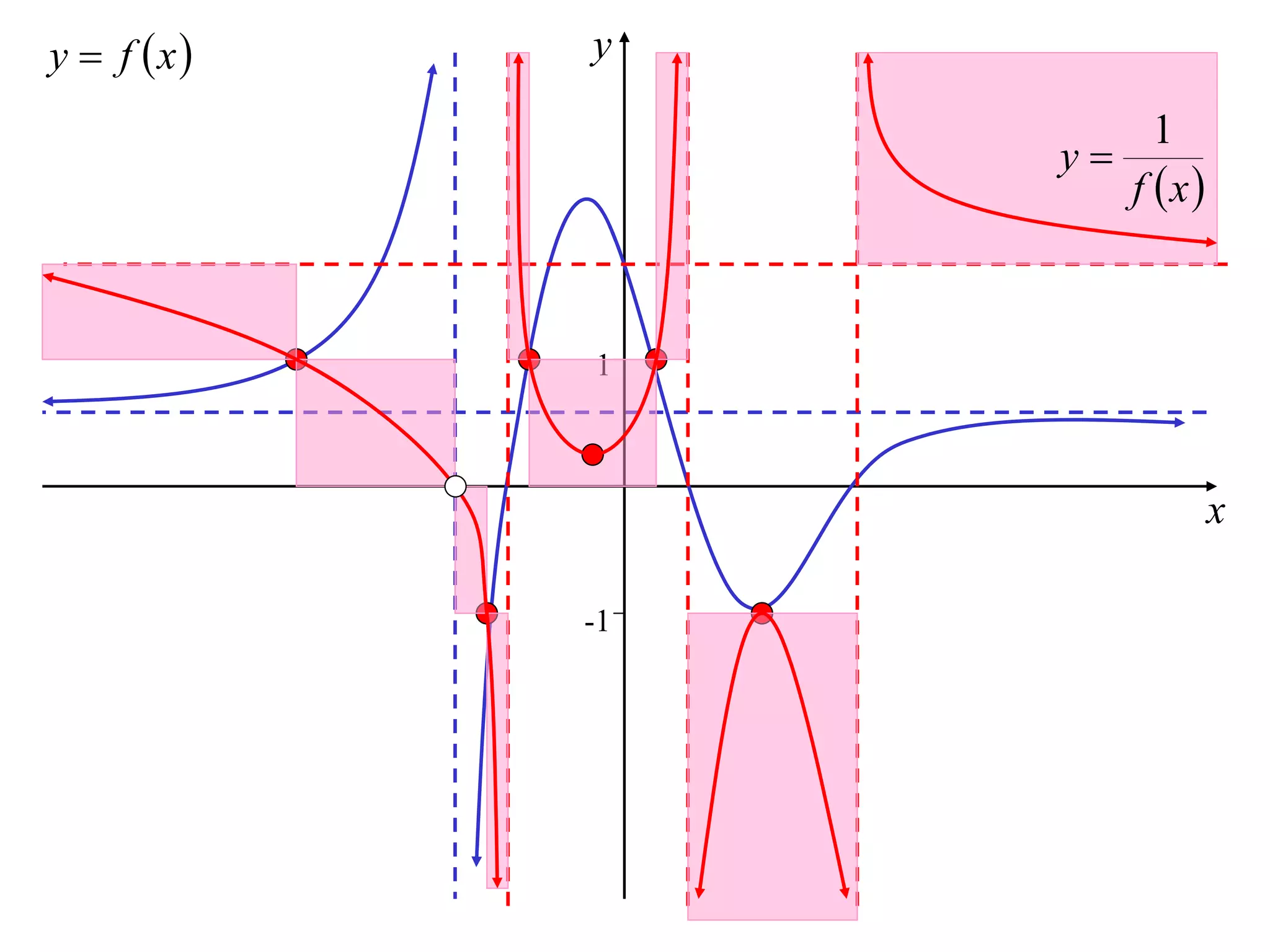
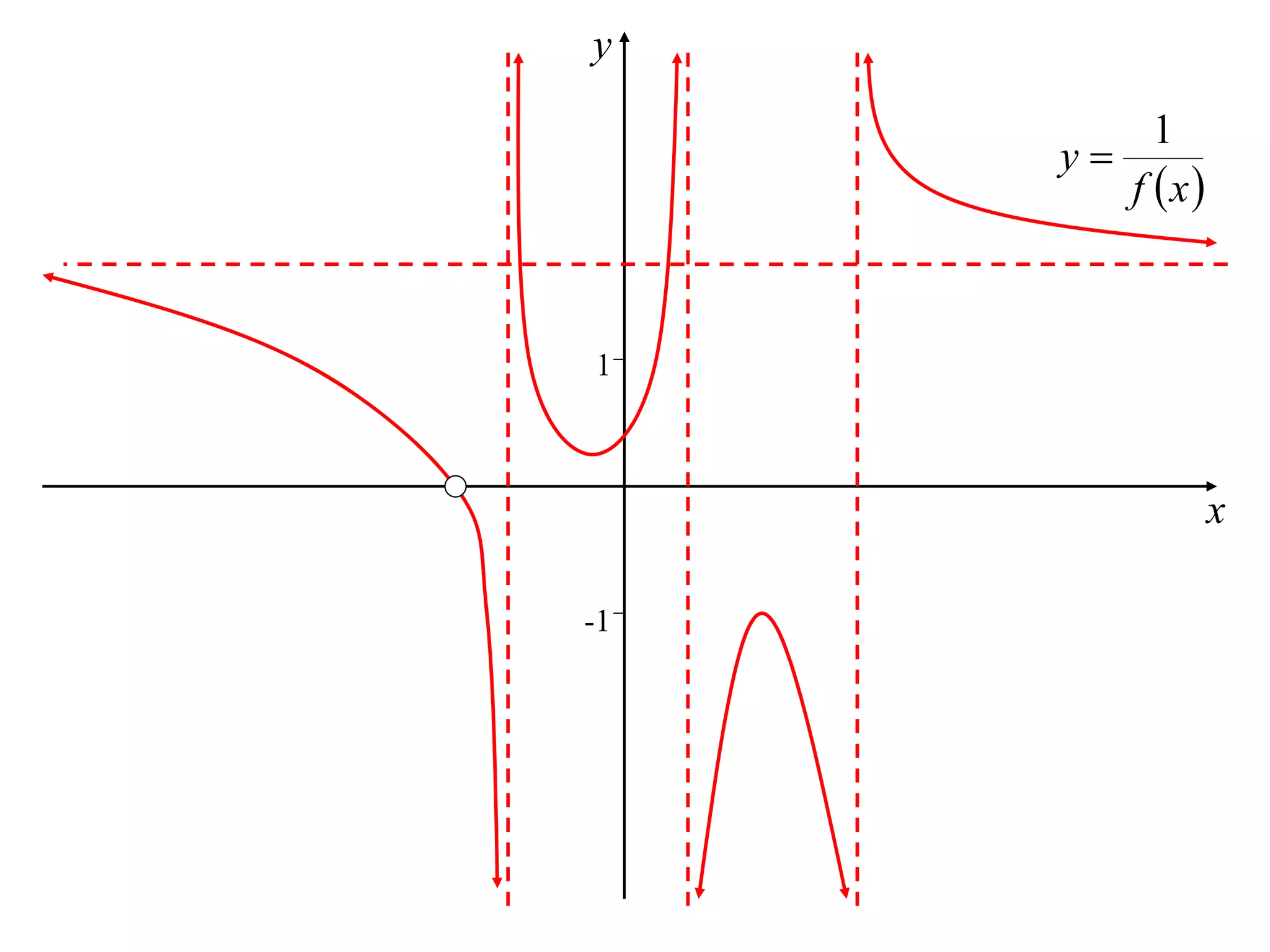
The document discusses how to sketch the graph of a reciprocal function y = 1/f(x). Key points include: 1) Vertical asymptotes occur where f(x) = 0. 2) Horizontal asymptotes occur where f(x) approaches infinity. 3) The graph of the reciprocal function is decreasing where the original function is increasing, and vice versa. 4) Stationary points of the original function correspond to stationary points of the reciprocal function.

1. (G) Graphs of Reciprocal
1
Functions
The graph of y  can be sketched by first drawing y  f  x 
f x
and noticing;

2. (G) Graphs of Reciprocal
1
Functions
The graph of y  can be sketched by first drawing y  f  x 
f x
and noticing;
1
 when f  x   0, then is undefined, i.e. a vertical asymptote exists 
f x

3. y  f x y
1
x
-1

4. y  f x y
1
x
-1

5. (G) Graphs of Reciprocal
1
Functions
The graph of y  can be sketched by first drawing y  f  x 
f x
and noticing;
1
 when f  x   0, then is undefined, i.e. a vertical asymptote exists 
f x
1
 when f  x   , then  0, i.e. asymptotes become x intercepts 
f x

6. y  f x y
1
x
-1

7. y  f x y
1
x
-1

8. y  f x y
1
x
-1

9. y  f x y
1
x
-1

10. (G) Graphs of Reciprocal
1
Functions
The graph of y  can be sketched by first drawing y  f  x 
f x
and noticing;
1
 when f  x   0, then is undefined, i.e. a vertical asymptote exists 
f x
1
 when f  x   , then  0, i.e. asymptotes become x intercepts 
f x
 when f  x  is increasing, the reciprocal is decreasing, and visa - versa

11. (G) Graphs of Reciprocal
1
Functions
The graph of y  can be sketched by first drawing y  f  x 
f x
and noticing;
1
 when f  x   0, then is undefined, i.e. a vertical asymptote exists 
f x
1
 when f  x   , then  0, i.e. asymptotes become x intercepts 
f x
 when f  x  is increasing, the reciprocal is decreasing, and visa - versa
1
 when f  x  is positive, is positive, etc.
f x

12. y  f x y
1
x
-1

13. (G) Graphs of Reciprocal
1
Functions
The graph of y  can be sketched by first drawing y  f  x 
f x
and noticing;
1
 when f  x   0, then is undefined, i.e. a vertical asymptote exists 
f x
1
 when f  x   , then  0, i.e. asymptotes become x intercepts 
f x
 when f  x  is increasing, the reciprocal is decreasing, and visa - versa
1
 when f  x  is positive, is positive, etc.
f x
1 -f  x 
 the derivative of is , hence stationary points of the
f  x   f  x  2
original curve are stationary points of its reciprocal.

14. y  f x y
1
x
-1

15. y  f x y
1
y
f x
1
x
-1

16. y
1
y
f x
1
x
-1