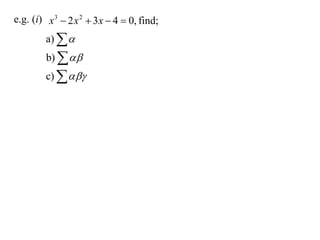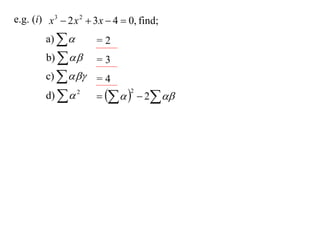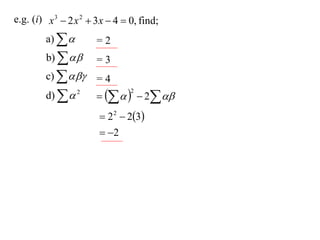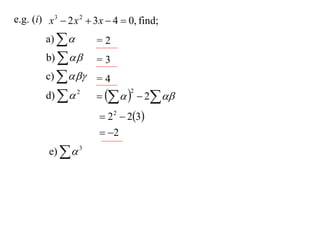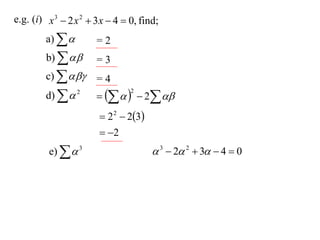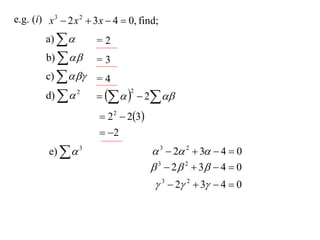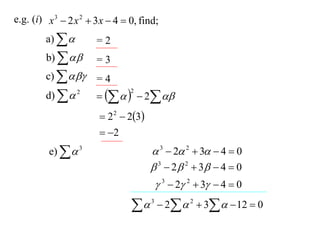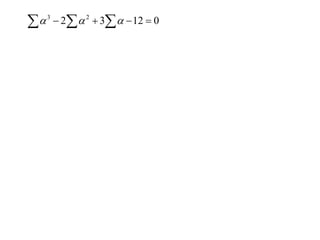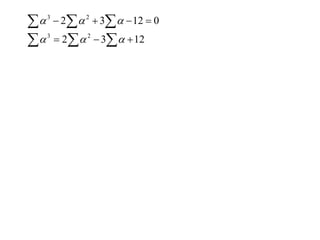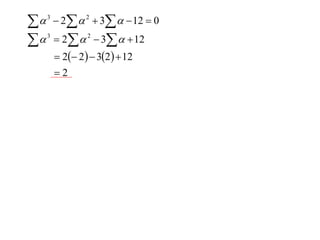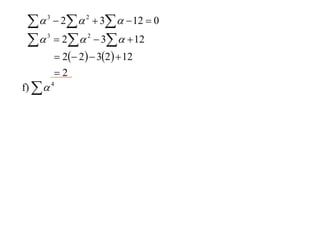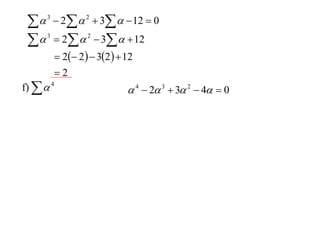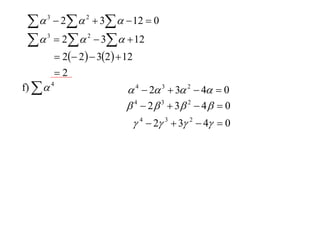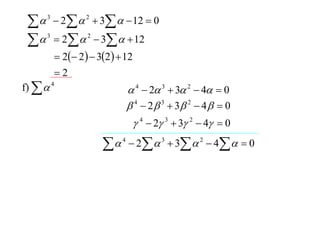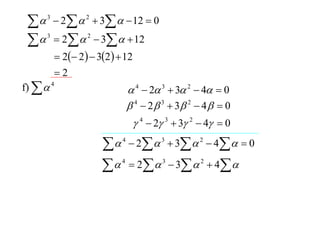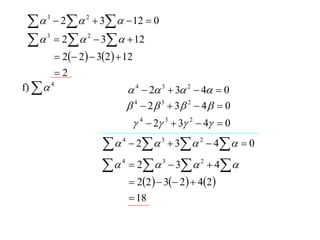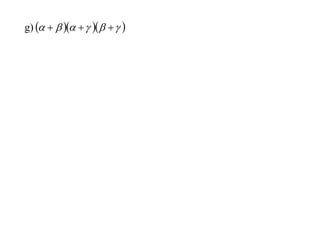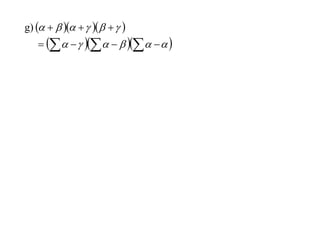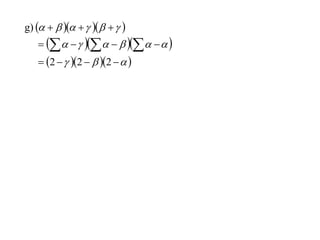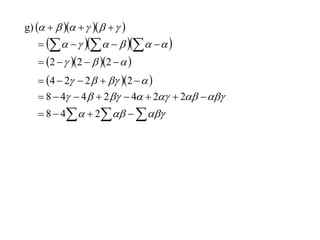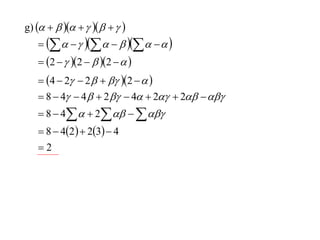The document discusses relationships between the coefficients and roots of polynomials. It states that for a polynomial P(x) = ax^n + bx^(n-1) + cx^(n-2) + ..., the sum of the roots is equal to -b/a, the sum of the roots taken two at a time is equal to c/a, and so on for higher order terms. It also generalizes relationships between symmetric polynomials of the roots. For example, the sum of the squares of the roots is equal to the square of the sum minus two times the sum of the roots taken two at a time. An example polynomial is worked out to illustrate finding its sums of roots.

1. Roots and Coefficients

2. Roots and Coefficients
For P x   ax n  bx n 1  cx n  2 

3. Roots and Coefficients
For P x   ax n  bx n 1  cx n  2 
b
  a (sum of roots, 1 at a time i.e.        )

4. Roots and Coefficients
For P x   ax n  bx n 1  cx n  2 
b
  a (sum of roots, 1 at a time i.e.        )
c
  
a
(sum of roots, 2 at a time i.e.       )

5. Roots and Coefficients
For P x   ax n  bx n 1  cx n  2 
b
  a (sum of roots, 1 at a time i.e.        )
c
  
a
(sum of roots, 2 at a time i.e.       )
d
  a (sum of roots, 3 at a time i.e.    )

6. Roots and Coefficients
For P x   ax n  bx n 1  cx n  2 
b
  a (sum of roots, 1 at a time i.e.        )
c
  
a
(sum of roots, 2 at a time i.e.       )
d
  a (sum of roots, 3 at a time i.e.    )
e
  a (sum of roots, 4 at a time)

7. We have already seen that for ax 2  bx  c ;
 2   2     2  2

8. We have already seen that for ax 2  bx  c ;
 2   2     2  2
and
1 1 
 
  

9. We have already seen that for ax 2  bx  c ;
 2   2     2  2
and
1 1 
 
  
This can be generalised to;

10. We have already seen that for ax 2  bx  c ;
 2   2     2  2
and
1 1 
 
  
This can be generalised to;
      2 
2 2

11. We have already seen that for ax 2  bx  c ;
 2   2     2  2
and
1 1 
 
  
This can be generalised to;
      2 
2 2
1 
    (order 2)

12. We have already seen that for ax 2  bx  c ;
 2   2     2  2
and
1 1 
 
  
This can be generalised to;
      2 
2 2
1 
    (order 2)
  (order 3)


13. We have already seen that for ax 2  bx  c ;
 2   2     2  2
and
1 1 
 
  
This can be generalised to;
      2 
2 2
1 
    (order 2)
  (order 3)

  (order 4)


14. e.g. (i) x 3  2 x 2  3 x  4  0, find;

15. e.g. (i) x 3  2 x 2  3 x  4  0, find;
a)  
b)   
c)   

16. e.g. (i) x 3  2 x 2  3 x  4  0, find;
a)   =2
b)    =3
c)    =4

17. e.g. (i) x 3  2 x 2  3 x  4  0, find;
a)   =2
b)    =3
c)    =4
d)   2

18. e.g. (i) x 3  2 x 2  3 x  4  0, find;
a)   =2
b)    =3
c)    =4
d)   2      2 
2

19. e.g. (i) x 3  2 x 2  3 x  4  0, find;
a)   =2
b)    =3
c)    =4
d)   2      2 
2
 2 2  23
 2

20. e.g. (i) x 3  2 x 2  3 x  4  0, find;
a)   =2
b)    =3
c)    =4
d)   2      2 
2
 2 2  23
 2
e)   3

21. e.g. (i) x 3  2 x 2  3 x  4  0, find;
a)   =2
b)    =3
c)    =4
d)   2      2 
2
 2 2  23
 2
e)   3  3  2 2  3  4  0

22. e.g. (i) x 3  2 x 2  3 x  4  0, find;
a)   =2
b)    =3
c)    =4
d)   2      2 
2
 2 2  23
 2
e)   3  3  2 2  3  4  0
 3  2  2  3  4  0
 3  2 2  3  4  0

23. e.g. (i) x 3  2 x 2  3 x  4  0, find;
a)   =2
b)    =3
c)    =4
d)   2      2 
2
 2 2  23
 2
e)   3  3  2 2  3  4  0
 3  2  2  3  4  0
 3  2 2  3  4  0
  3  2  2  3   12  0

24.   3  2  2  3   12  0

25.   3  2  2  3   12  0
  3  2  2  3   12

26.   3  2  2  3   12  0
  3  2  2  3   12
 2 2   32   12
2

27.   3  2  2  3   12  0
  3  2  2  3   12
 2 2   32   12
2
f)   4

28.   3  2  2  3   12  0
  3  2  2  3   12
 2 2   32   12
2
f)   4  4  2 3  3 2  4  0

29.   3  2  2  3   12  0
  3  2  2  3   12
 2 2   32   12
2
f)   4  4  2 3  3 2  4  0
 4  2  3  3 2  4   0
 4  2 3  3 2  4  0

30.   3  2  2  3   12  0
  3  2  2  3   12
 2 2   32   12
2
f)   4  4  2 3  3 2  4  0
 4  2  3  3 2  4   0
 4  2 3  3 2  4  0
  4  2  3  3  2  4   0

31.   3  2  2  3   12  0
  3  2  2  3   12
 2 2   32   12
2
f)   4  4  2 3  3 2  4  0
 4  2  3  3 2  4   0
 4  2 3  3 2  4  0
  4  2  3  3  2  4   0
  4  2  3  3  2  4 

32.   3  2  2  3   12  0
  3  2  2  3   12
 2 2   32   12
2
f)   4  4  2 3  3 2  4  0
 4  2  3  3 2  4   0
 4  2 3  3 2  4  0
  4  2  3  3  2  4   0
  4  2  3  3  2  4 
 22   3 2   42 
 18

33. g)           

34. g)           
             

35. g)           
             
 2   2   2   

36. g)           
             
 2   2   2   
 4  2  2    2   
 8  4  4   2   4  2  2  
 8  4   2    

37. g)           
             
 2   2   2   
 4  2  2    2   
 8  4  4   2   4  2  2  
 8  4   2    
 8  42   23  4
2

38. (ii) (1996)
Consider the polynomial equation x 4  ax 3  bx 2  cx  d  0
where a, b, c and d are all integers.
Suppose the equation has a root of the form ki, where k is real
and k  0

39. (ii) (1996)
Consider the polynomial equation x 4  ax 3  bx 2  cx  d  0
where a, b, c and d are all integers.
Suppose the equation has a root of the form ki, where k is real
and k  0
a) State why the conjugate –ki is also a root.

40. (ii) (1996)
Consider the polynomial equation x 4  ax 3  bx 2  cx  d  0
where a, b, c and d are all integers.
Suppose the equation has a root of the form ki, where k is real
and k  0
a) State why the conjugate –ki is also a root.
Roots appear in conjugate pairs when the coefficients are real.

41. (ii) (1996)
Consider the polynomial equation x 4  ax 3  bx 2  cx  d  0
where a, b, c and d are all integers.
Suppose the equation has a root of the form ki, where k is real
and k  0
a) State why the conjugate –ki is also a root.
Roots appear in conjugate pairs when the coefficients are real.
b) Show that c  k 2 a

42. (ii) (1996)
Consider the polynomial equation x 4  ax 3  bx 2  cx  d  0
where a, b, c and d are all integers.
Suppose the equation has a root of the form ki, where k is real
and k  0
a) State why the conjugate –ki is also a root.
Roots appear in conjugate pairs when the coefficients are real.
b) Show that c  k 2 a
x 4  ax 3  bx 2  cx  d   x  ki  x  ki x 2  px  q 

43. (ii) (1996)
Consider the polynomial equation x 4  ax 3  bx 2  cx  d  0
where a, b, c and d are all integers.
Suppose the equation has a root of the form ki, where k is real
and k  0
a) State why the conjugate –ki is also a root.
Roots appear in conjugate pairs when the coefficients are real.
b) Show that c  k 2 a
x 4  ax 3  bx 2  cx  d   x  ki  x  ki x 2  px  q 
 x 2  k 2 x 2  px  q 
 x 4  px 3  qx 2  k 2 x 2  k 2 px  k 2 q
 x 4  px 3  q  k 2 x 2  k 2 px  k 2 q

44. (ii) (1996)
Consider the polynomial equation x 4  ax 3  bx 2  cx  d  0
where a, b, c and d are all integers.
Suppose the equation has a root of the form ki, where k is real
and k  0
a) State why the conjugate –ki is also a root.
Roots appear in conjugate pairs when the coefficients are real.
b) Show that c  k 2 a
x 4  ax 3  bx 2  cx  d   x  ki  x  ki x 2  px  q 
 x 2  k 2 x 2  px  q 
 x 4  px 3  qx 2  k 2 x 2  k 2 px  k 2 q
 x 4  px 3  q  k 2 x 2  k 2 px  k 2 q
 p  a  (1) q  k 2  b  (2) k 2 p  c  (3) k 2 q  d  (4)

45. (ii) (1996)
Consider the polynomial equation x 4  ax 3  bx 2  cx  d  0
where a, b, c and d are all integers.
Suppose the equation has a root of the form ki, where k is real
and k  0
a) State why the conjugate –ki is also a root.
Roots appear in conjugate pairs when the coefficients are real.
b) Show that c  k 2 a
x 4  ax 3  bx 2  cx  d   x  ki  x  ki x 2  px  q 
 x 2  k 2 x 2  px  q 
 x 4  px 3  qx 2  k 2 x 2  k 2 px  k 2 q
 x 4  px 3  q  k 2 x 2  k 2 px  k 2 q
 p  a  (1) q  k 2  b  (2) k 2 p  c  (3) k 2 q  d  (4)
Substitute (1) into (3)

46. (ii) (1996)
Consider the polynomial equation x 4  ax 3  bx 2  cx  d  0
where a, b, c and d are all integers.
Suppose the equation has a root of the form ki, where k is real
and k  0
a) State why the conjugate –ki is also a root.
Roots appear in conjugate pairs when the coefficients are real.
b) Show that c  k 2 a
x 4  ax 3  bx 2  cx  d   x  ki  x  ki x 2  px  q 
 x 2  k 2 x 2  px  q 
 x 4  px 3  qx 2  k 2 x 2  k 2 px  k 2 q
 x 4  px 3  q  k 2 x 2  k 2 px  k 2 q
 p  a  (1) q  k 2  b  (2) k 2 p  c  (3) k 2 q  d  (4)
Substitute (1) into (3) k 2a  c

47. c) Show that c 2  a 2 d  abc

48. c) Show that c 2  a 2 d  abc
Using (2); q  b  k 2

49. c) Show that c 2  a 2 d  abc
Using (2); q  b  k 2
Sub into (4); k 2 b  k 2   d

50. c) Show that c 2  a 2 d  abc
Using (2); q  b  k 2
Sub into (4); k 2 b  k 2   d
bk 2  k 4  d

51. c) Show that c 2  a 2 d  abc
Using (2); q  b  k 2
Sub into (4); k 2 b  k 2   d
bk 2  k 4  d
bc c 2
 2 d
a a

52. c) Show that c 2  a 2 d  abc
Using (2); q  b  k 2
Sub into (4); k 2 b  k 2   d
bk 2  k 4  d
bc c 2 c
 2 d ( k 2  )
a a a

53. c) Show that c 2  a 2 d  abc
Using (2); q  b  k 2
Sub into (4); k 2 b  k 2   d
bk 2  k 4  d
bc c 2 c
 2 d ( k 2  )
a a a
abc  c 2  a 2 d

54. c) Show that c 2  a 2 d  abc
Using (2); q  b  k 2
Sub into (4); k 2 b  k 2   d
bk 2  k 4  d
bc c 2 c
 2 d ( k 2  )
a a a
abc  c 2  a 2 d
c 2  a 2 d  abc

55. d) If 2 is also a root of the equation, and b = 0, show that c is even.

56. d) If 2 is also a root of the equation, and b = 0, show that c is even.
Let  be the 4th root

57. d) If 2 is also a root of the equation, and b = 0, show that c is even.
Let  be the 4th root
As the other three roots are integer multiples, and the product of
the roots is an integer;
 is an integer

58. d) If 2 is also a root of the equation, and b = 0, show that c is even.
Let  be the 4th root
As the other three roots are integer multiples, and the product of
the roots is an integer;
 is an integer
 ki ki   2 ki   2ki     ki    ki   2  b

59. d) If 2 is also a root of the equation, and b = 0, show that c is even.
Let  be the 4th root
As the other three roots are integer multiples, and the product of
the roots is an integer;
 is an integer
 ki ki   2 ki   2ki     ki    ki   2  b   

60. d) If 2 is also a root of the equation, and b = 0, show that c is even.
Let  be the 4th root
As the other three roots are integer multiples, and the product of
the roots is an integer;
 is an integer
 ki ki   2 ki   2ki     ki    ki   2  b   
k 2  2  0
k 2  2

61. d) If 2 is also a root of the equation, and b = 0, show that c is even.
Let  be the 4th root
As the other three roots are integer multiples, and the product of
the roots is an integer;
 is an integer
 ki ki   2 ki   2ki     ki    ki   2  b   
k 2  2  0
k 2  2
From c)  c  k 2 a

62. d) If 2 is also a root of the equation, and b = 0, show that c is even.
Let  be the 4th root
As the other three roots are integer multiples, and the product of
the roots is an integer;
 is an integer
 ki ki   2 ki   2ki     ki    ki   2  b   
k 2  2  0
k 2  2
From c)  c  k 2 a
c  2a

63. d) If 2 is also a root of the equation, and b = 0, show that c is even.
Let  be the 4th root
As the other three roots are integer multiples, and the product of
the roots is an integer;
 is an integer
 ki ki   2 ki   2ki     ki    ki   2  b   
k 2  2  0
k 2  2
From c)  c  k 2 a
c  2a
c  2M

64. d) If 2 is also a root of the equation, and b = 0, show that c is even.
Let  be the 4th root
As the other three roots are integer multiples, and the product of
the roots is an integer;
 is an integer
 ki ki   2 ki   2ki     ki    ki   2  b   
k 2  2  0
k 2  2
From c)  c  k 2 a
c  2a
c  2 M  and a are both integers, M is an integer

65. d) If 2 is also a root of the equation, and b = 0, show that c is even.
Let  be the 4th root
As the other three roots are integer multiples, and the product of
the roots is an integer;
 is an integer
 ki ki   2 ki   2ki     ki    ki   2  b   
k 2  2  0
k 2  2
From c)  c  k 2 a
c  2a
c  2 M  and a are both integers, M is an integer
Thus c is an even number, as it is divisible by 2

66. Exercise 5D; 1 to 9