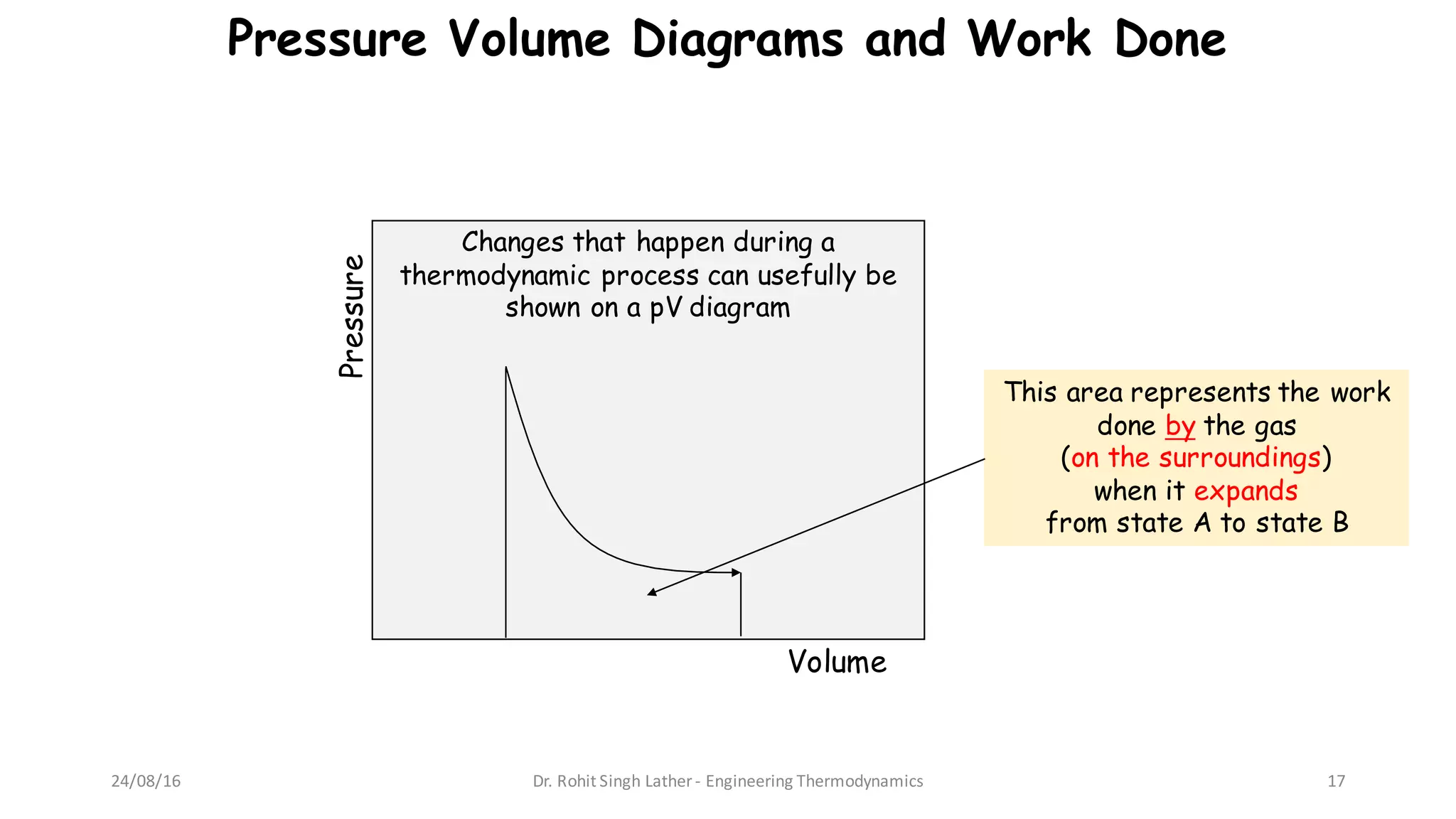
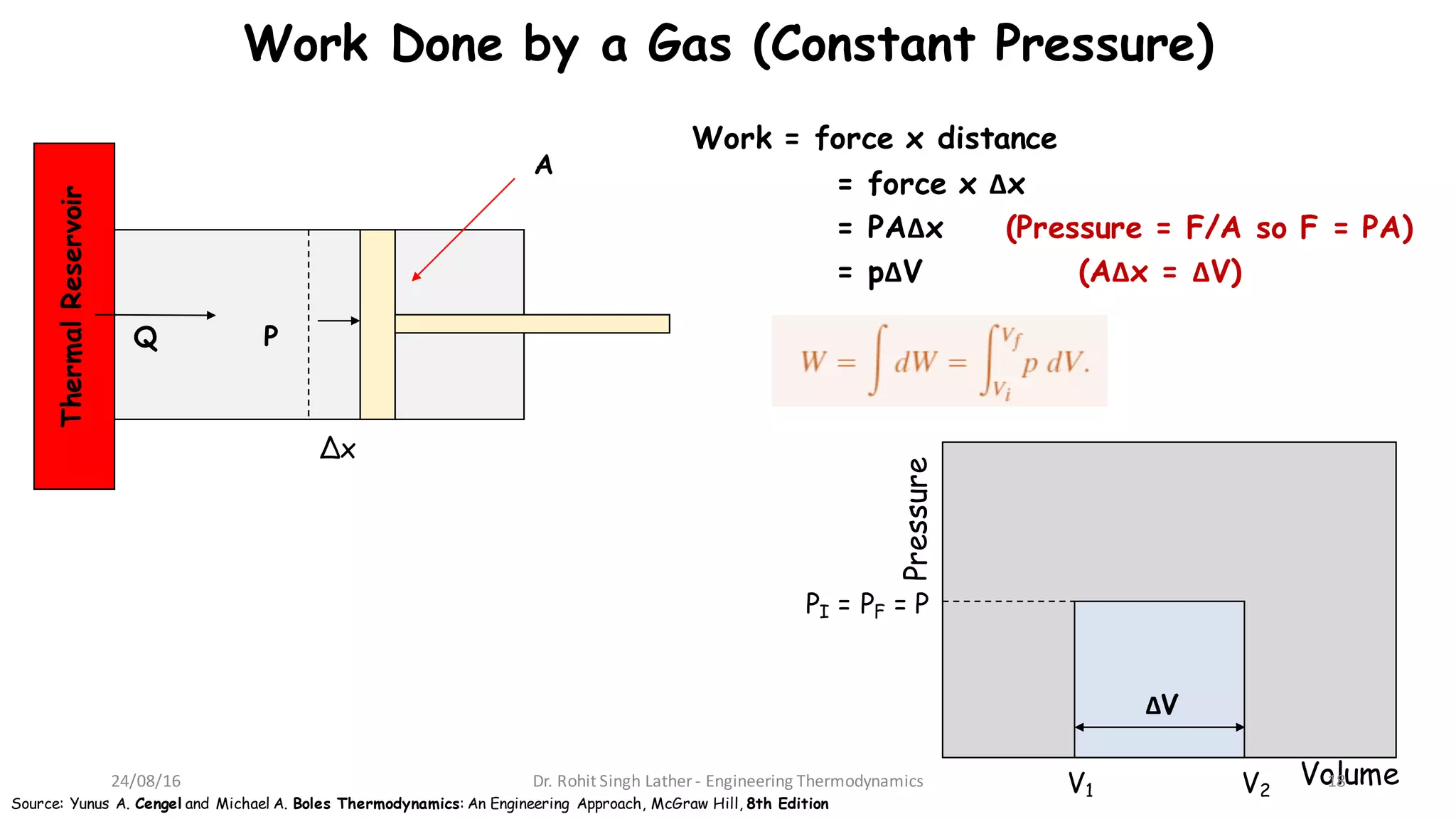
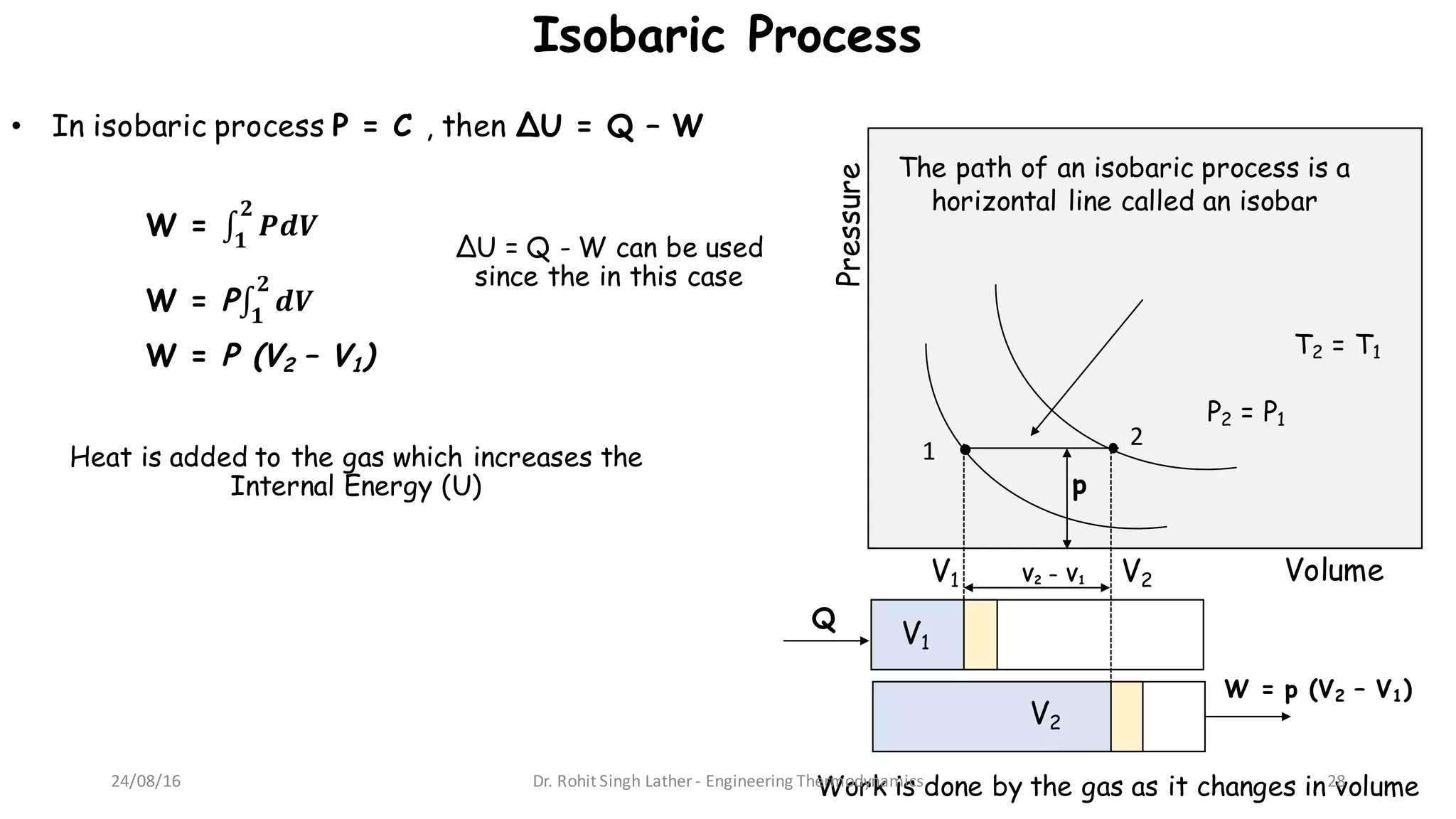
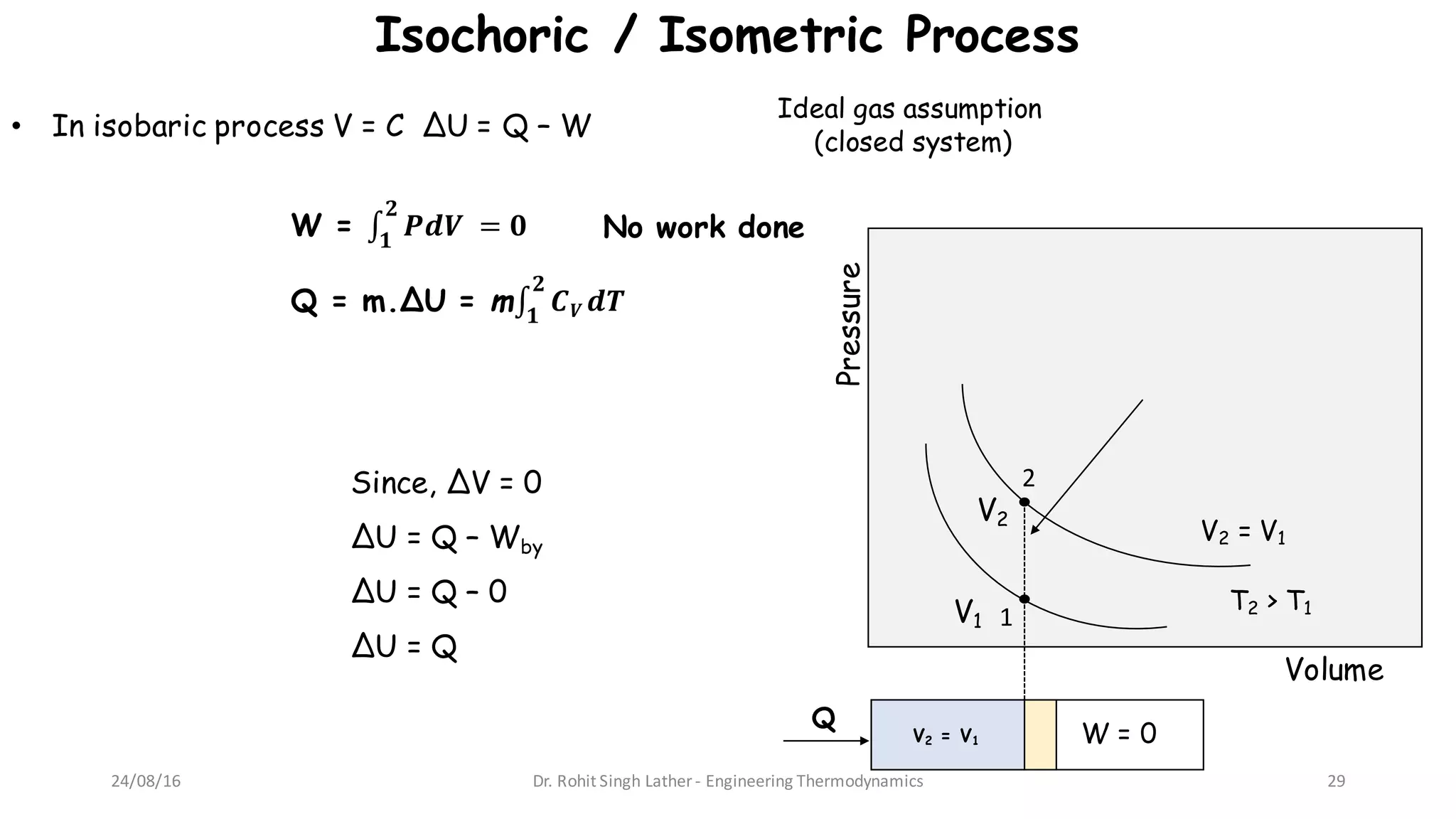
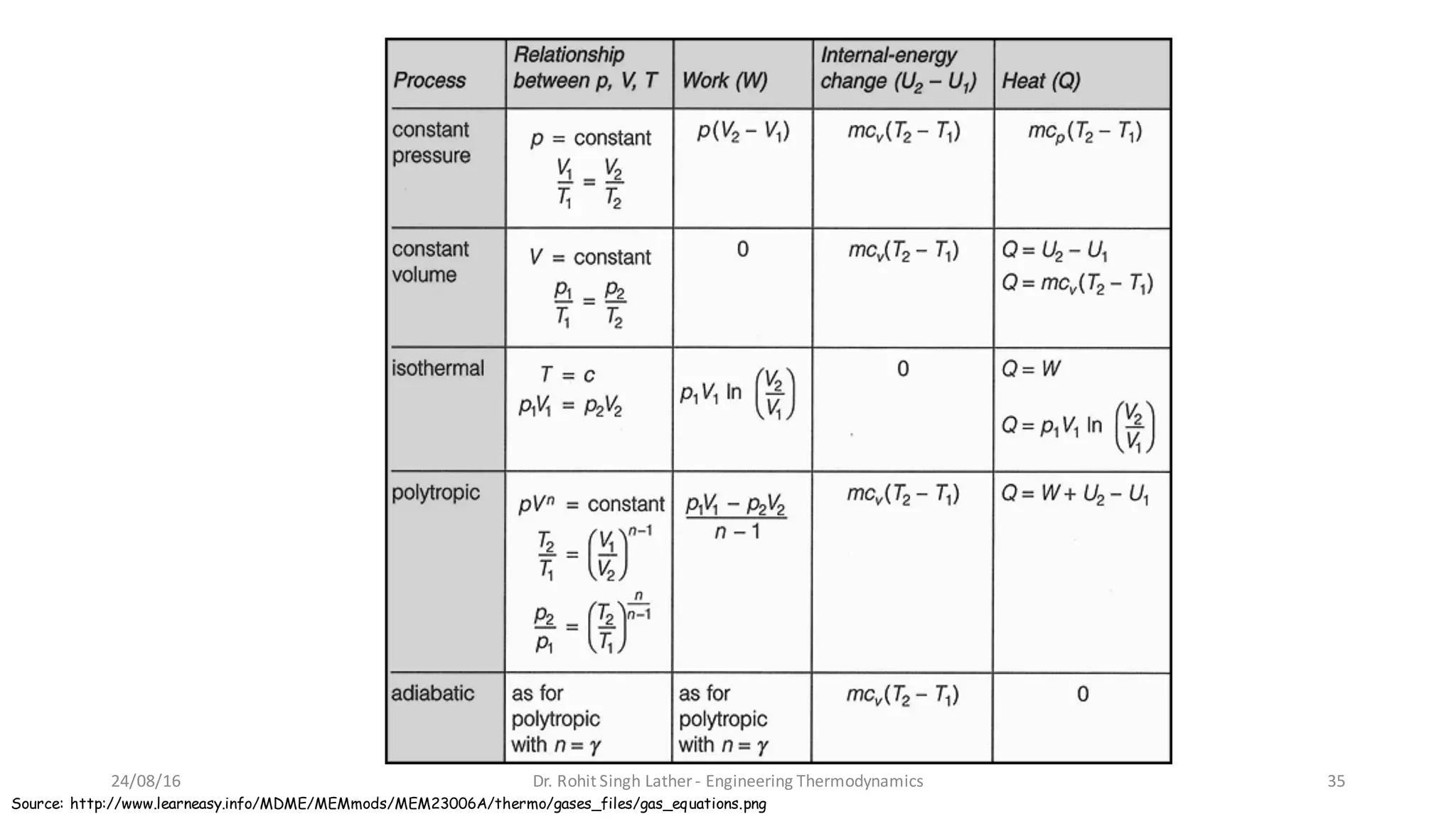
1) The document discusses different forms and modes of energy transfer including heat, work, internal energy, and kinetic and potential energy at both the macroscopic and microscopic levels.
2) Heat is defined as the random motion of particles and is identified as energy crossing system boundaries, while work involves a direct transfer of energy between a system and its surroundings.
3) The specific heat of a material is the amount of heat required to change its temperature by one degree, while heat of transformation (latent heat) is the energy required for phase changes like melting or vaporization.








![• For ideal gases Cv, and Cp are related by: Cp = Cv + R [kJ / (kg.K)]
• The specific heat ratio 𝛾 is defined as: 𝛾 =
𝑪 𝒑
𝑪 𝒗
• For incompressible substances (liquids and solids), both the constant-pressure and
constant-volume specific heats are identical and denoted by C:
Cp = Cv = C [kJ / (kg.K)]
Source: Yunus A. Cengel and Michael A. Boles Thermodynamics: An Engineering Approach, McGraw Hill, 8th Edition
Cp > Cv In an isobaric process system is heated and work is performed
CV CP
Monoatomic Gases %
&
R
%
&
R
Diatomic Gases %
&
R
%
&
R
Triatomic Gases %
&
R
%
&
R
24/08/16 Dr. Rohit Singh Lather - Engineering Thermodynamics 10](https://image.slidesharecdn.com/workandheat-170118101302/75/Work-and-heat-10-2048.jpg)