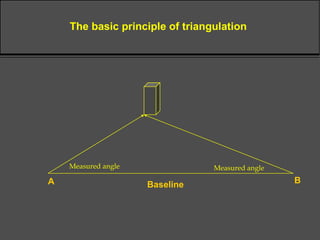
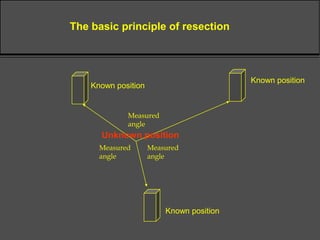
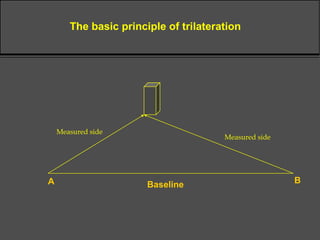
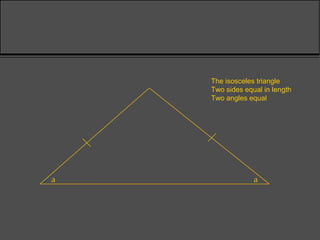
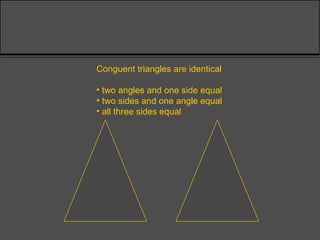
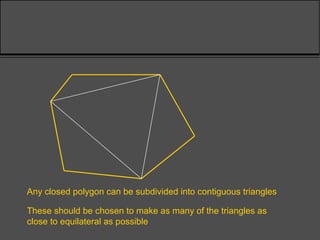
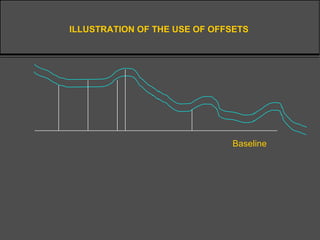
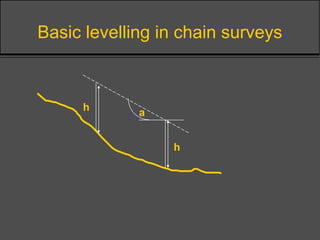
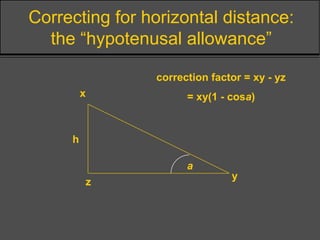
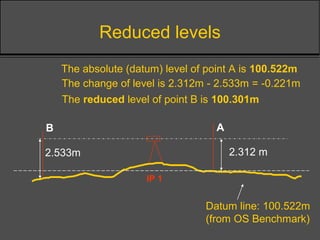
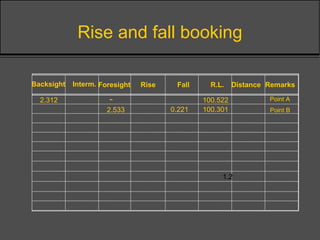
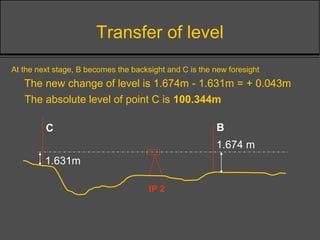
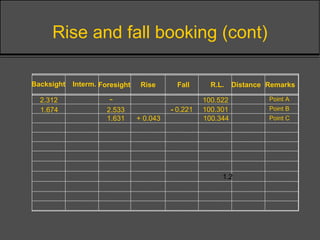
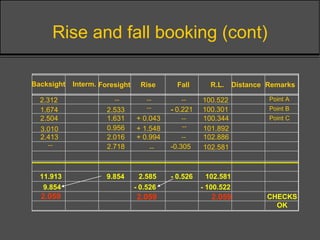
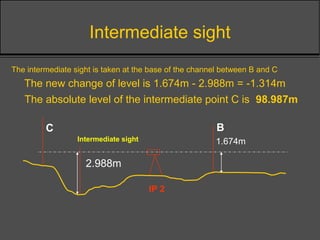
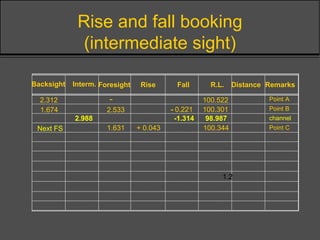
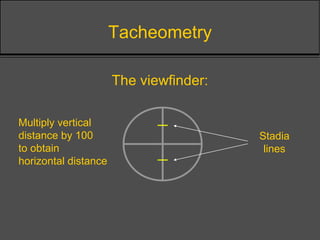
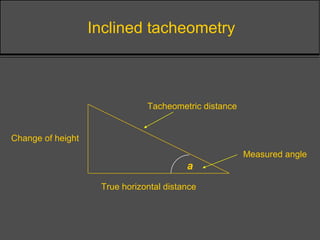
Surveying techniques are used to establish the position of objects in 2D or 3D. Primary surveys are done when no previous data exists, while secondary surveys add to existing data or measure changes. Plan position is determined through techniques like triangulation, trilateration, or offset measurements from baselines. Elevation is found by direct or inclined leveling between points of known height. Theodolites allow simultaneous measurement of horizontal angles, slopes, and slant distances.

1. A2.2NP1
Environmental Practical 1
TOPIC 1
TECHNIQUES IN
BASIC SURVEYING

2. Basic ideas
• Surveying - the creation of a scale representation of
the ground surface - is a basic activity in many areas
of environmental management.
• A survey will be one of of two types:
– Primary survey - to establish the position of objects in three
dimensions when no previous information exists
– Secondary survey - to add extra information to existing
data or to measure changes over an interval of time

3. Basic ideas
• The task of three dimensional position fixing
is normally broken into two parts:
• Determining plan position
• Determining elevation

4. Basic ideas
• Each of these determinations may be either:
• absolute - made in terms of a fixed co-ordinate
system
• relative - made in terms of local co-ordinates
which may later be converted to absolute co-
ordinates if required.
• The majority of surveys carried out for
environmental management are thus
secondary relative surveys

5. Plan Position Fixing
• The plan position of a station can be
established in a number of ways:

6. • By reference to the apparent positions
of astronomical objects when viewed
from that station
• This method gives the absolute location of
the station in terms of latitude and longitude,
which can be converted to local systems such
as the National Grid.

7. • By the measurement of the angles between lines
of sight to the unknown station from other known
positions
• By the intersection of lines of sight from the
unknown station to other objects whose positions
are already known
• These two methods both rely on the simple Euclidean
geometry of the plane. (Hence the term plane surveying).
The first procedure is termed triangulation and the
second resection.

8. BaselineA B
The basic principle of triangulation
Measured angle Measured angle

9. Unknown position
The basic principle of resection
Measured
angle
Measured
angle
Known position
Known position
Known position
Measured
angle

10. • By measurement of distances between
the unknown station and other objects
of known positions
• This last method includes a number of
particular cases:

11. • measurements of offset distances from
a base line.
• trilateration - the distance equivalent of
triangulation.
• tacheometry - an optical method of
distance measurement along a known
bearing

12. BaselineA B
The basic principle of trilateration
Measured side
Measured side

13. Plane Surveying: Theory
• Plane surveying relies on the basic
concepts of Euclidean geometry, and in
particular the properties of triangles.
• The most important (for our purposes)
of these are:

14. Plane Surveying: Theory
• The internal angles of a triangle sum to 180°
• The sides of an equilateral triangle are equal
and the internal angles are all 60°
• The base angles and opposing sides of an
isosceles triangle are equal

15. 60º
60º 60º
The equilateral triangle
All sides equal in length
All angles equal (= 60º)

16. The isosceles triangle
Two sides equal in length
Two angles equal
a a

17. Plane Surveying: Theory
• If the respective angles in two triangles are
equal then the triangles are similar and their
sides are all in the same proportion
• If two triangles have two angles and one side
equal (or vice versa) then they are congruent
and all their other respective angles and
sides are equal.
• Two triangles are also congruent if all their
sides are equal.

18. Similar triangles have corresponding angles equal
but are of differing size

19. Conguent triangles are identical
• two angles and one side equal
• two sides and one angle equal
• all three sides equal

20. Plane Surveying: Theory
• Congruent triangles are unique - you cannot
draw two different triangles from the same set
of measurements
• This means that a complete set of survey
data must define the positions of objects
uniquely.

21. Plane Surveying: Theory
• Any closed polygon can be subdivided into a
series of contiguous triangles
• These properties are repeatedly used in the
procedure of triangulation in which stations
are surveyed in a pattern of contiguous
triangles.

22. Any closed polygon can be subdivided into contiguous triangles
These should be chosen to make as many of the triangles as
close to equilateral as possible

23. Plane surveying: practical aspects
• In practice, most plane surveys are carried out
in a straightforward way following an
established sequence:
1. A reconnaisance survey will establish the
dimensions of the area, relative levels,
significant features, accessibility, obstacles etc

24. Plane surveying: practical aspects
2. Establish an accurate baseline by measurement
from existing survey points, natural features,
buildings etc. If none are available then the baseline
must be fixed by absolute methods.
3. Establish as required any further control points by
triangulation or trilateration from the base-line.

25. Plane surveying: practical aspects
4. Incorporate detail by tacheometry, traversing, tape &
offset or whatever other method is appropriate.
5. The intermediate stations should where appropriate
be cross-checked with the control points by resection
and all traverses should be closed at a control point.
6. Inaccessible detail should be incorporated by
triangulation or plane tabling from the ends of the
baseline.

26. Baseline
ILLUSTRATION OF THE USE OF OFFSETS

27. Plane surveying: practical aspects
7. If a topographic survey is being undertaken, levelling
traverses should be carried out around the survey
stations and the baseline tied to the local benchmark
by a closed traverse.
8. The use of a theodolite or total station will enable
both the position and the elevation of stations to be
found simultaneously by combined tacheometry and
triangulation or by trilateration

28. THE “CHAIN” SURVEY
How to establish relative plan positions

29. Chain survey
• Simplest of all survey techniques
• Relies on linear measurements; slopes
>3o
require some adjustment to technique
• Usually requires a clear line of sight
• The triangles used should be equilateral
or approximately so

30. Terminology
• Trilateration is the measurement of
sides of a triangle
• whereas triangulation refers to the
measurement of the angles of the
triangle

31. Basic equipment
• Ranging poles
• Survey pegs and ‘arrows’
• Chain & tape measure or other distance
measuring instrument
• Plumb line
• Compass

32. Chain survey components
• Base line: the longest line
• Chain /survey lines
• Survey stations
• Offset lines

33. Order of events
• “Range out” survey stations with ranging rods
• Establish base line and measure accurately
• Measure remaining distances between other
survey stations
• Measure offset lines whilst measuring
between survey stations

34. Sloping ground
• If the ground slopes by more than about 3°,
this must be allowed for in the survey.
• The measured distances are thus slant
distances and must be corrected to true
horizontal distances.
• This requires that the vertical angle between
the stations is known

35. Ground distance determined
a
h
X

36. Sloping ground
• For an approximate survey, it may be
sufficient to step up or downhill using a
series of horizontal and vertical lines
• If the drop is measured at the same
time, some estimate of the slope profile
can be obtained

37. Chain surveying (“stepping”)
w
x
y
z
c
b
a

38. Sloping ground
• If stepping is not appropriate, more
sophisticated methods must be used to
measure the slant distance and the
vertical angle simultaneously
• Requires optical sighting equipment:
usually either a clinometer, Abney level
or theodolite

39. Basic levelling in chain surveys
a
h
h

40. Correcting for horizontal distance:
the “hypotenusal allowance”
a
h
z
correction factor = xy - yz
= xy(1 - cosa)
y
x

41. LEVELLING
How to destermine relative
elevations

42. Levelling:
accounting for slopes
Unlike chain surveys, levelling surveys
account directly for slope and
incorporate this data into the whole
measurement exercise
AIMS:
• to determine height differences
between two points
• to determine elevations for sections

43. • The elevation of a station can be
established by:
• inclined line of sight from chain survey stations
• levelling from another point of known height
• by inclined tacheometry

44. • Levelling is the more accurate method but is
also the slower. Modern instruments are
capable of cm accuracy under normal
conditions over distances of 100’s metres.
• The keys to successful levelling lie in the
setting up of the instrument, in the closure of
the traverses and in the careful recording
(booking) of the results.

45. • Inclined tacheometry relies on the combined
measurement, by theodolite, of the slant
distance to the new station and the angle
relative to the horizontal.
• The elevation change and horizontal distance
can then be found by simple trigonometry.
• The accuracy of the method, using normal
instruments, is around 10’s cms in 100’s
metres.

46. Direct levelling
• Most typical form used
Relies upon:
• a horizontal line of sight, also termed
“the line of collimation”
• a fixed datum level

47. Measurements to be taken
• Backsight
• Foresight
• Intermediate sights

48. Booking your results
The “rise and fall” method
• This method records the relative
change in level between successive
stations
• The changes are converted to the
reduced level of each station
• The reduced level is relative to the local
datum

49. Booking the results
• The method relies on recording your
results in a survey book in a standard
format
• This allows you to check your work and
to identify any errors systematically

50. Reduced levels
The change of level is 2.312m - 2.533m = -0.221m
2.533m
Datum line: 100.522m
(from OS Benchmark)
2.312 m
The reduced level of point B is 100.301m
B A
The absolute (datum) level of point A is 100.522m
IP 1

51. Backsight Interm. Foresight Rise Fall R.L. Distance Remarks
2.312 100.522
0.221 100.301
1.2
Rise and fall booking
Point A
Point B
-
2.533

52. Transfer of level
The new change of level is 1.674m - 1.631m = + 0.043m
1.631m
1.674 m
The absolute level of point C is 100.344m
C B
At the next stage, B becomes the backsight and C is the new foresight
IP 2

53. Backsight Interm. Foresight Rise Fall R.L. Distance Remarks
2.312 100.522
- 0.221 100.301
1.2
Rise and fall booking (cont)
Point A
Point B
-
2.5331.674
1.631 + 0.043 100.344 Point C

54. • Continuing this process, suppose we
end up with a set of results as follows:
• This will enable us to check our working

55. Backsight Interm. Foresight Rise Fall R.L. Distance Remarks
2.312 100.522
- 0.221 100.301
Rise and fall booking (cont)
Point A
Point B
--
2.5331.674
1.631 + 0.043 100.344 Point C2.504
3.010
2.413
0.956
2.016
2.718
--
--
--
--
+ 1.548
+ 0.994
-0.305
101.892
102.886
-- --
--
--
102.581
11.913
9.854
9.854 2.585
- 0.526
- 0.526 102.581
- 100.522
2.059 2.059 2.059 CHECKS
OK

56. Using an intermediate sight
• Sometimes we wish to include a
specific feature but it is not convenient
to set up a new instrument position for
this
• The solution is to take a sighting onto
the staff when it is placed on this
feature - this is called an intermediate
sight

57. Intermediate sight
The new change of level is 1.674m - 2.988m = -1.314m
2.988m
The absolute level of the intermediate point C is 98.987m
C B
The intermediate sight is taken at the base of the channel between B and C
IP 2
Intermediate sight 1.674m

58. Backsight Interm. Foresight Rise Fall R.L. Distance Remarks
2.312 100.522
- 0.221 100.301
1.2
Rise and fall booking
(intermediate sight)
Point A
Point B
-
2.5331.674
1.631 + 0.043 100.344 Point C
2.988 channel-1.314 98.987
Next FS

59. Optical distance measurement
• It is often convenient to use the levelling
instrument itself to calculate the distance
between the instrument and staff positions
• This is done using the stadia lines that are
visible in the viewfinder
• These are arranged such that the distance to
the staff is 100x the stadia interval that is
read on the staff between the two lines
• This procedure is known as tacheometry

60. Tacheometry
The viewfinder:
Stadia
lines
Multiply vertical
distance by 100
to obtain
horizontal distance

61. Inclined tacheometry
• If the ‘level’ can be swung in a vertical
arc, the distance up an inclined sight
line can be obtained.
• If the vertical angle is also measured,
the slant distance can be converted to
give both the change in height and the
true horizontal distance.

62. Inclined tacheometry
a
Change of height
Tacheometric distance
Measured angle
True horizontal distance

63. The theodolite
• If such an instrument can also be swung in a
horizontal arc, and the angle of rotation can
be measured, we are able to determine the
angles of the sight lines between stations.
• This allows both trilateration and triangulation
with the same instrument.
• Such a versatile instrument exist and is called
a theodolite.

64. Summary
• Chain surveys are suited to planimetric
surveys on low slopes. They rely upon
trilateration.
• Levelling is used where terrain is more
uneven. Levelling surveys often use
tacheometry to fix station positions.
• A theodolite survey permits levelling,
tacheometry or triangulation as required.