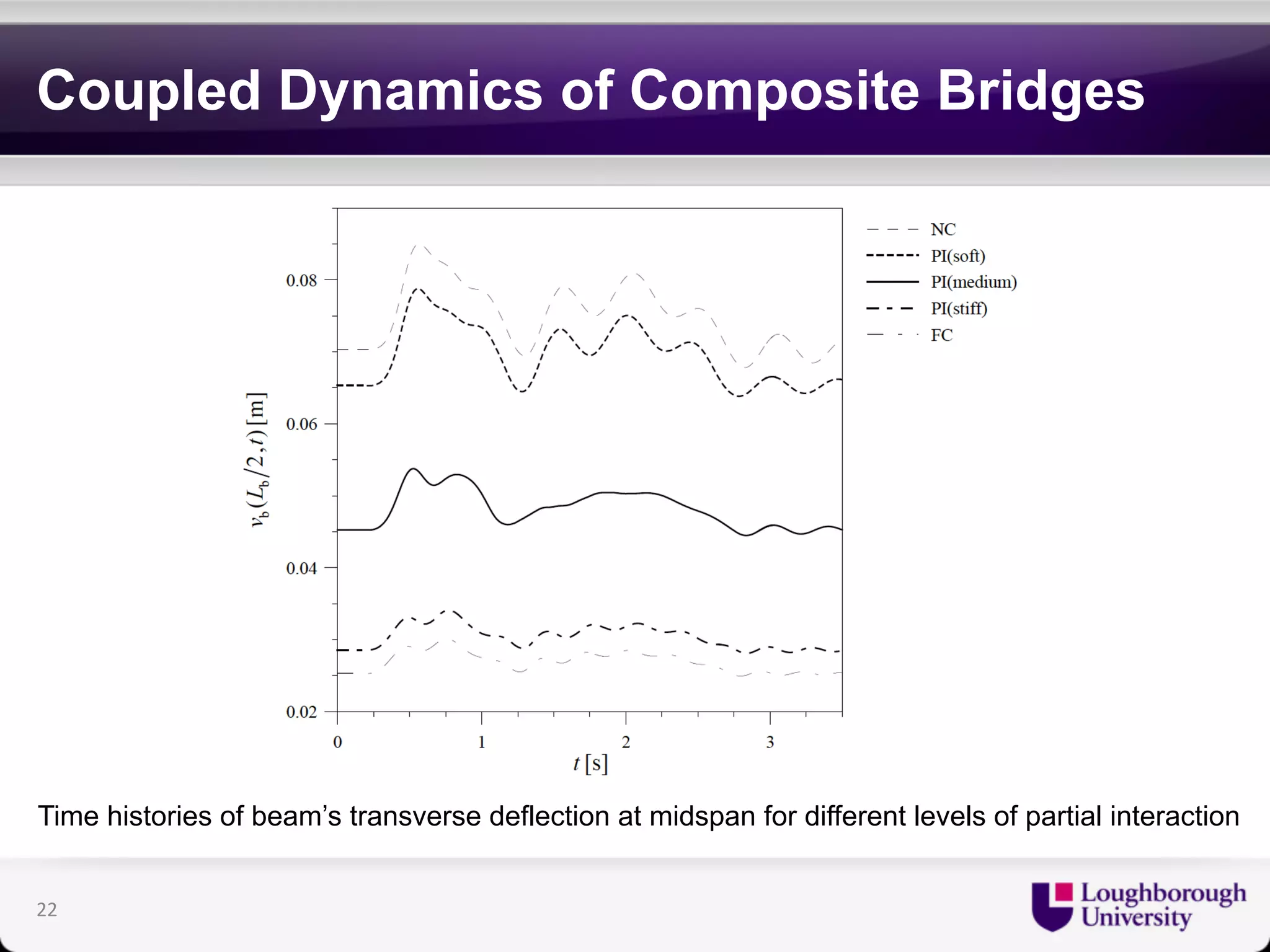
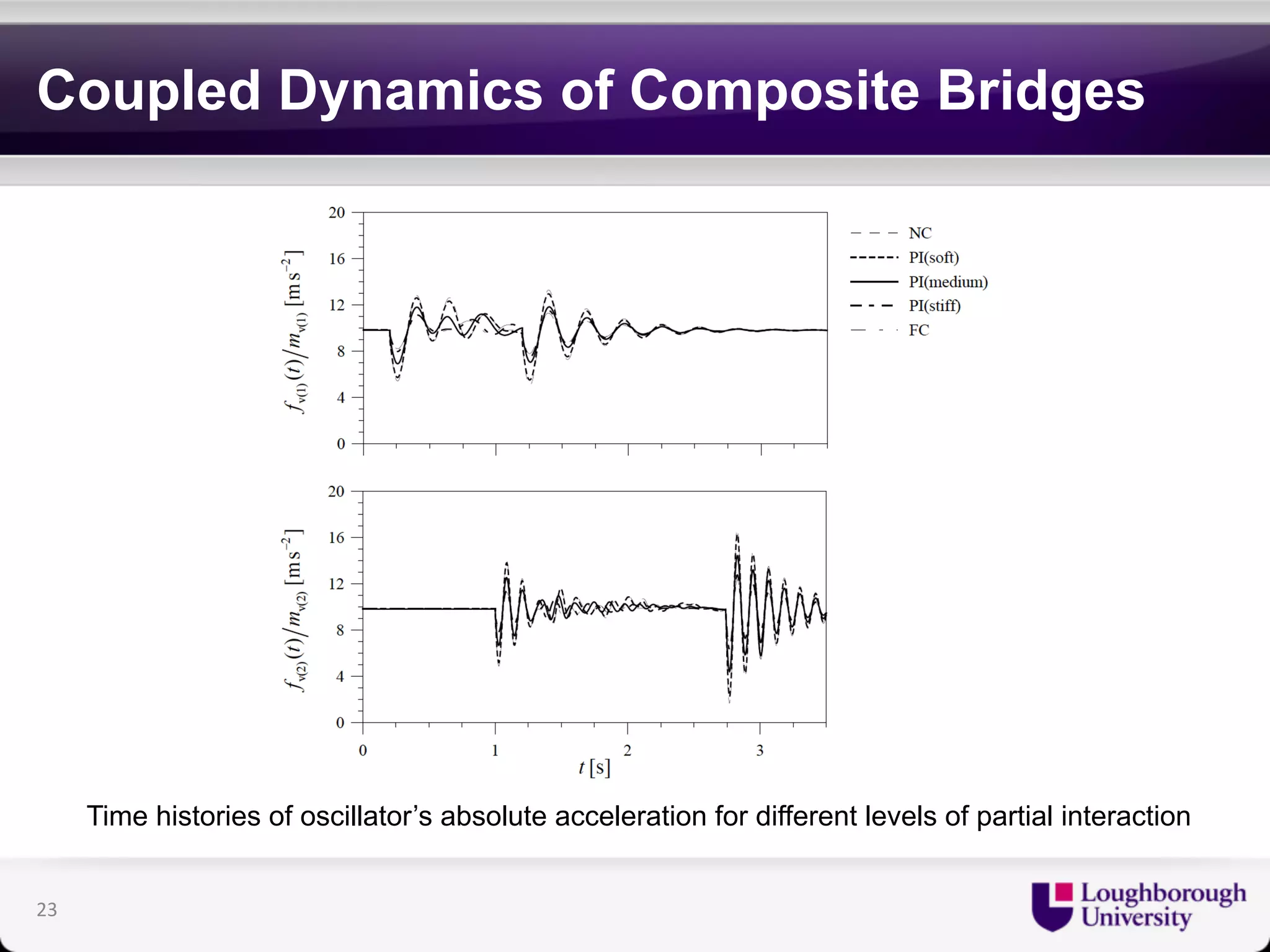
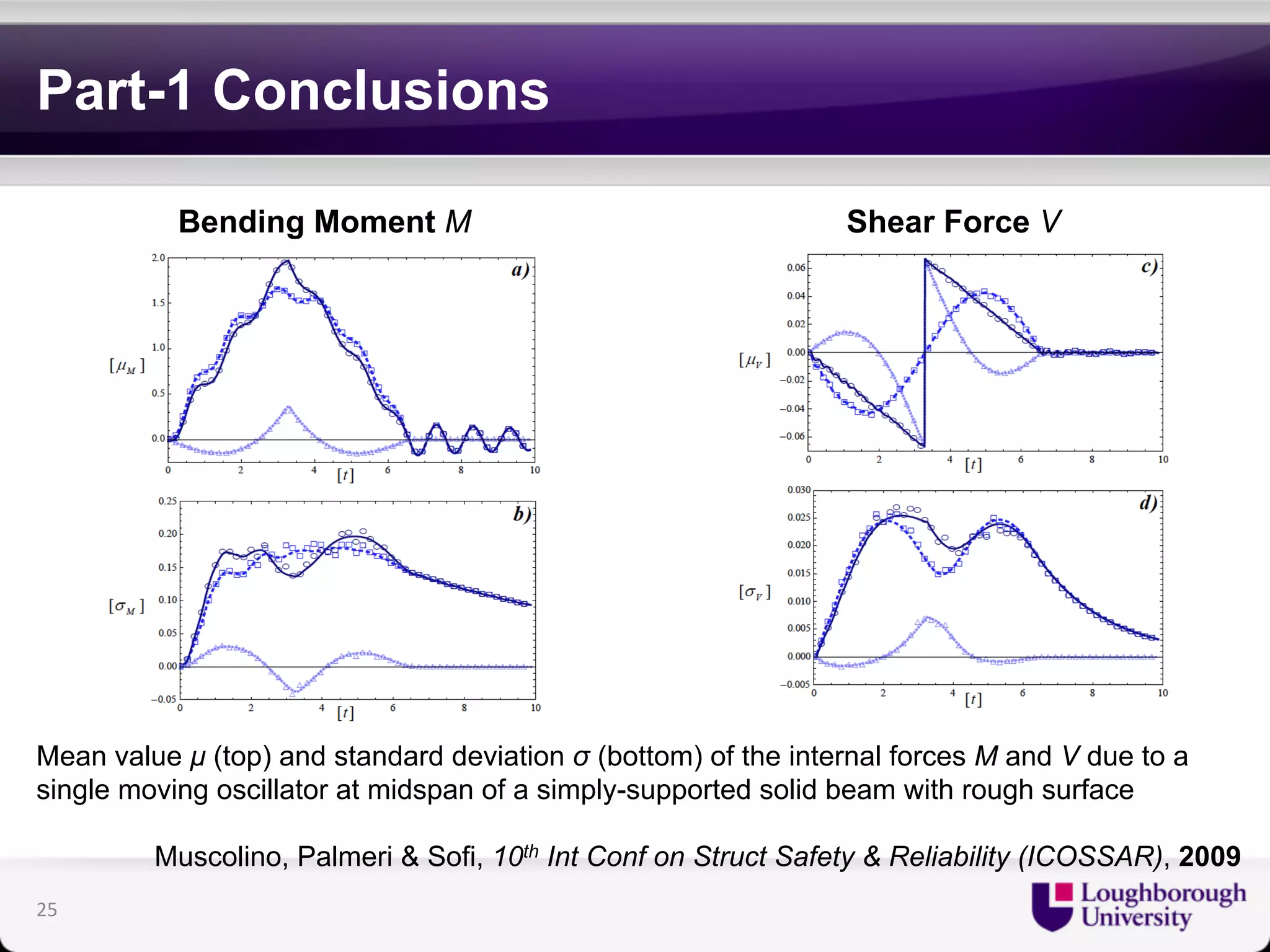
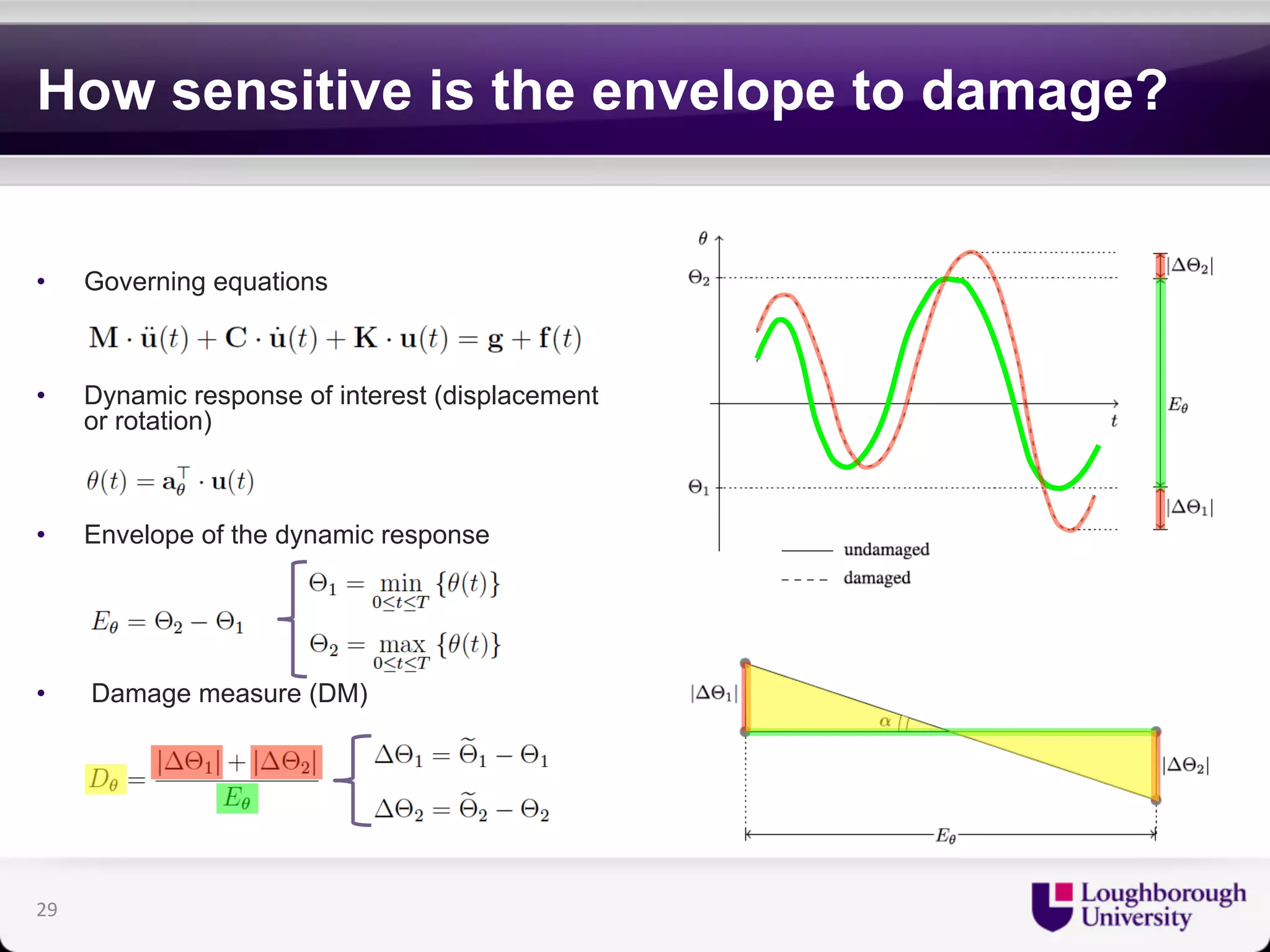
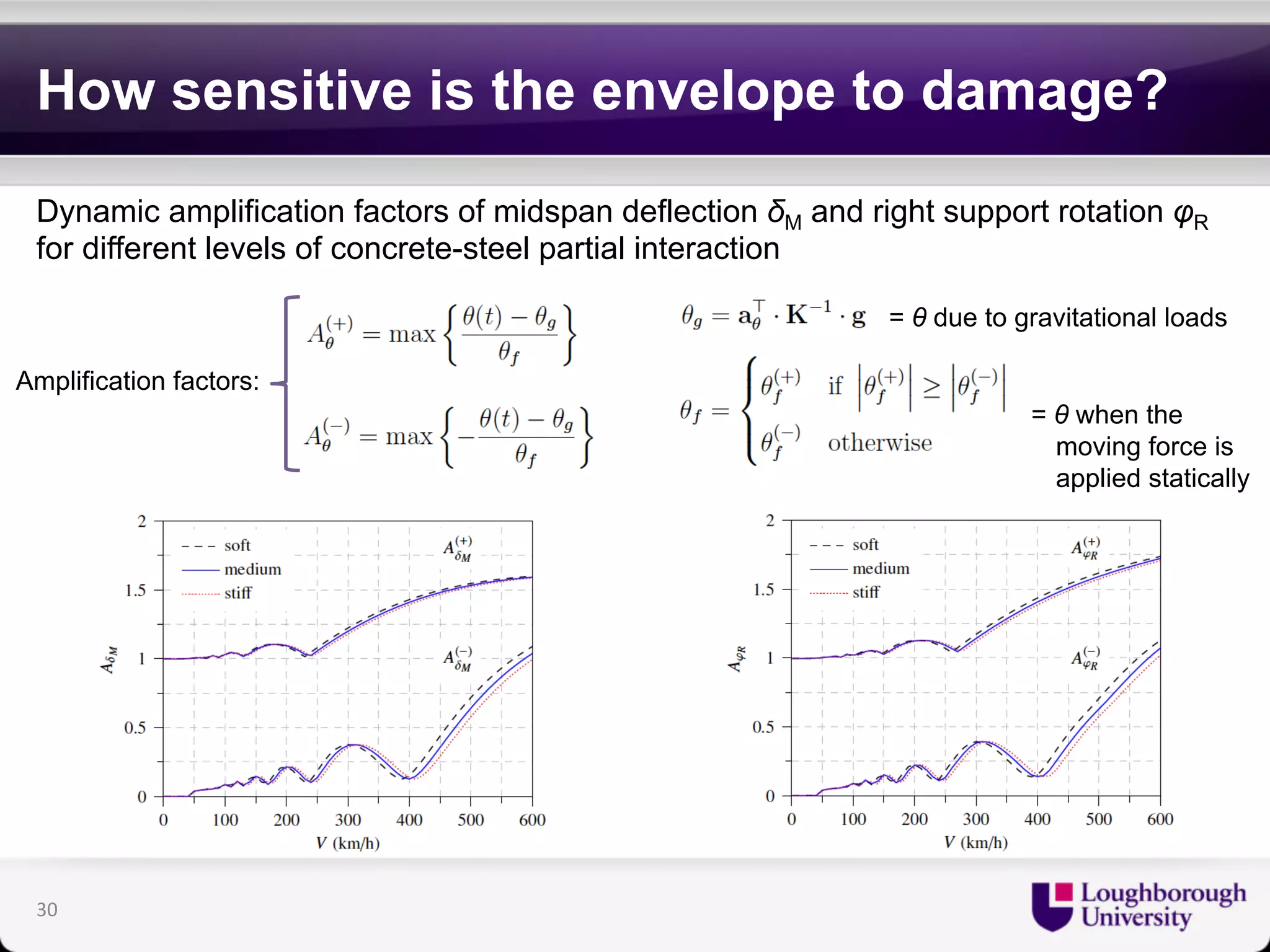
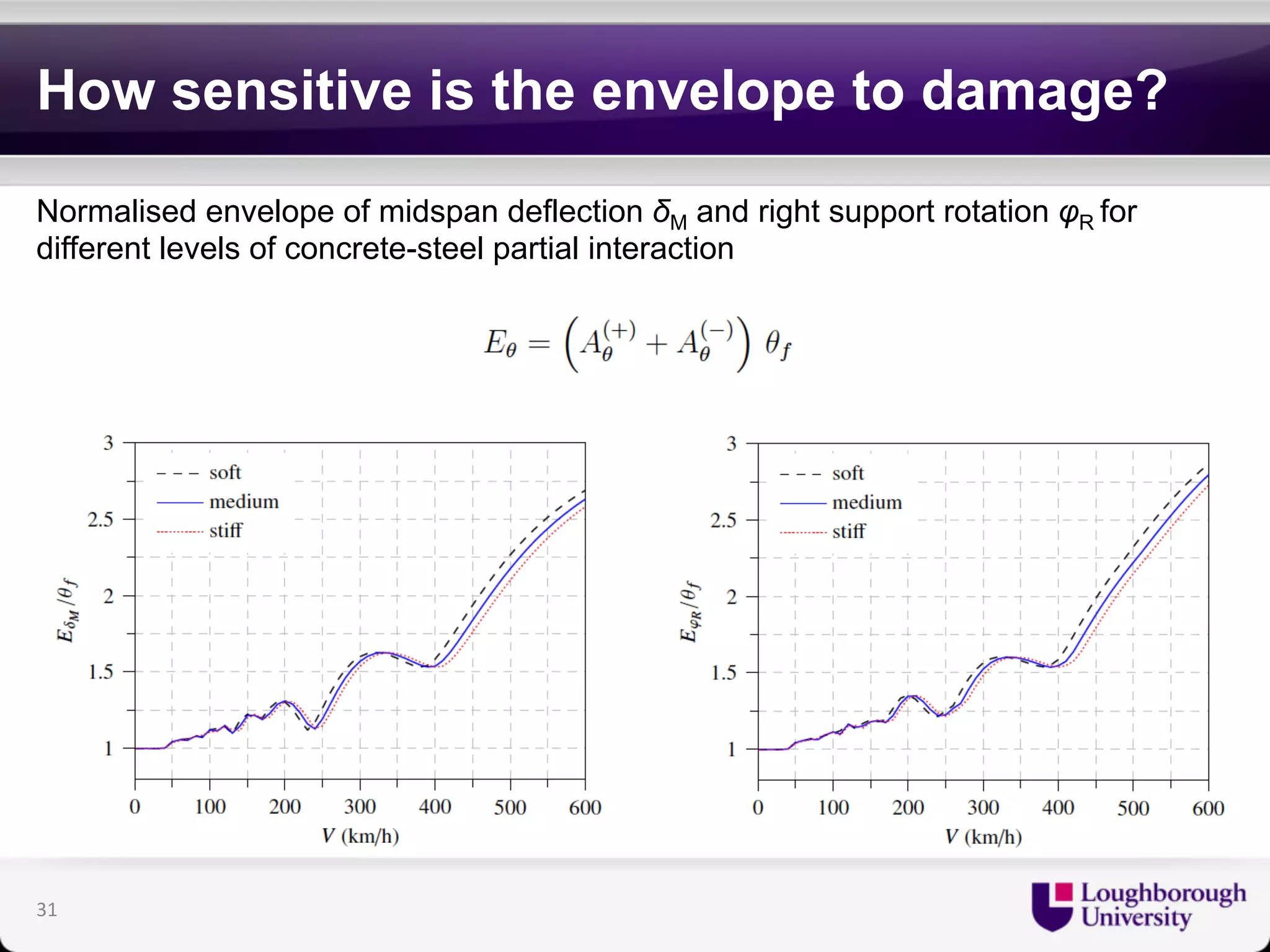
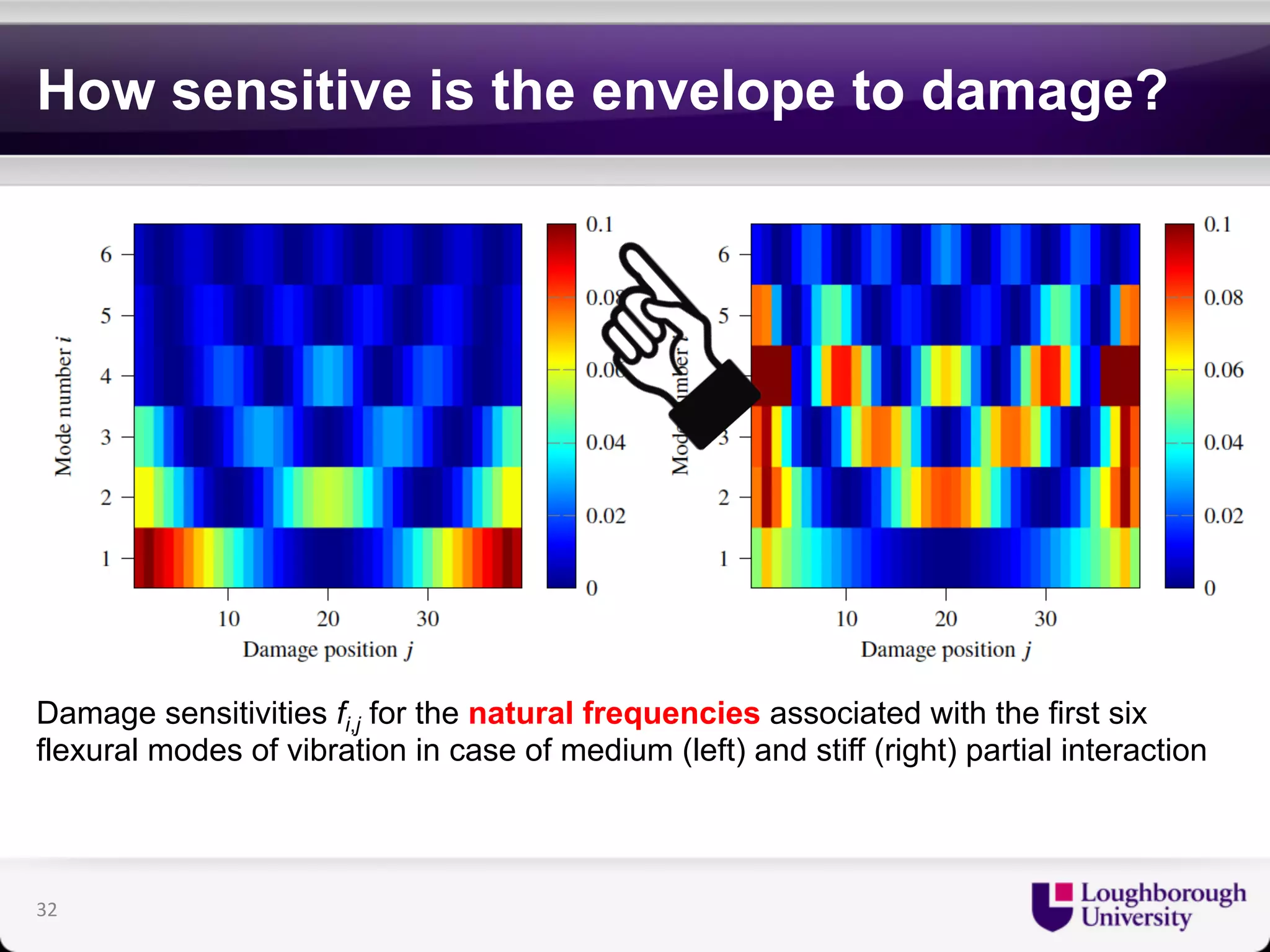
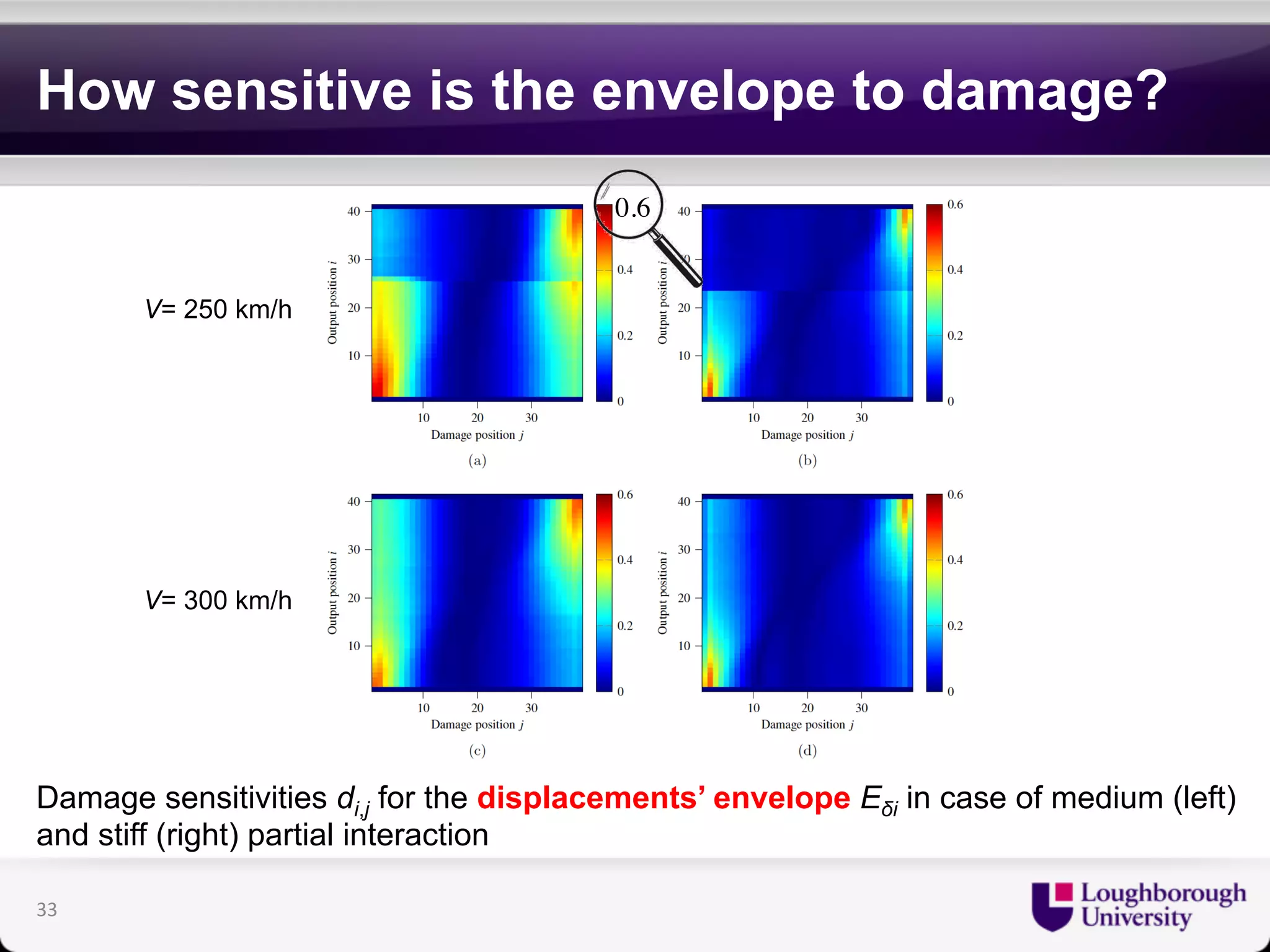
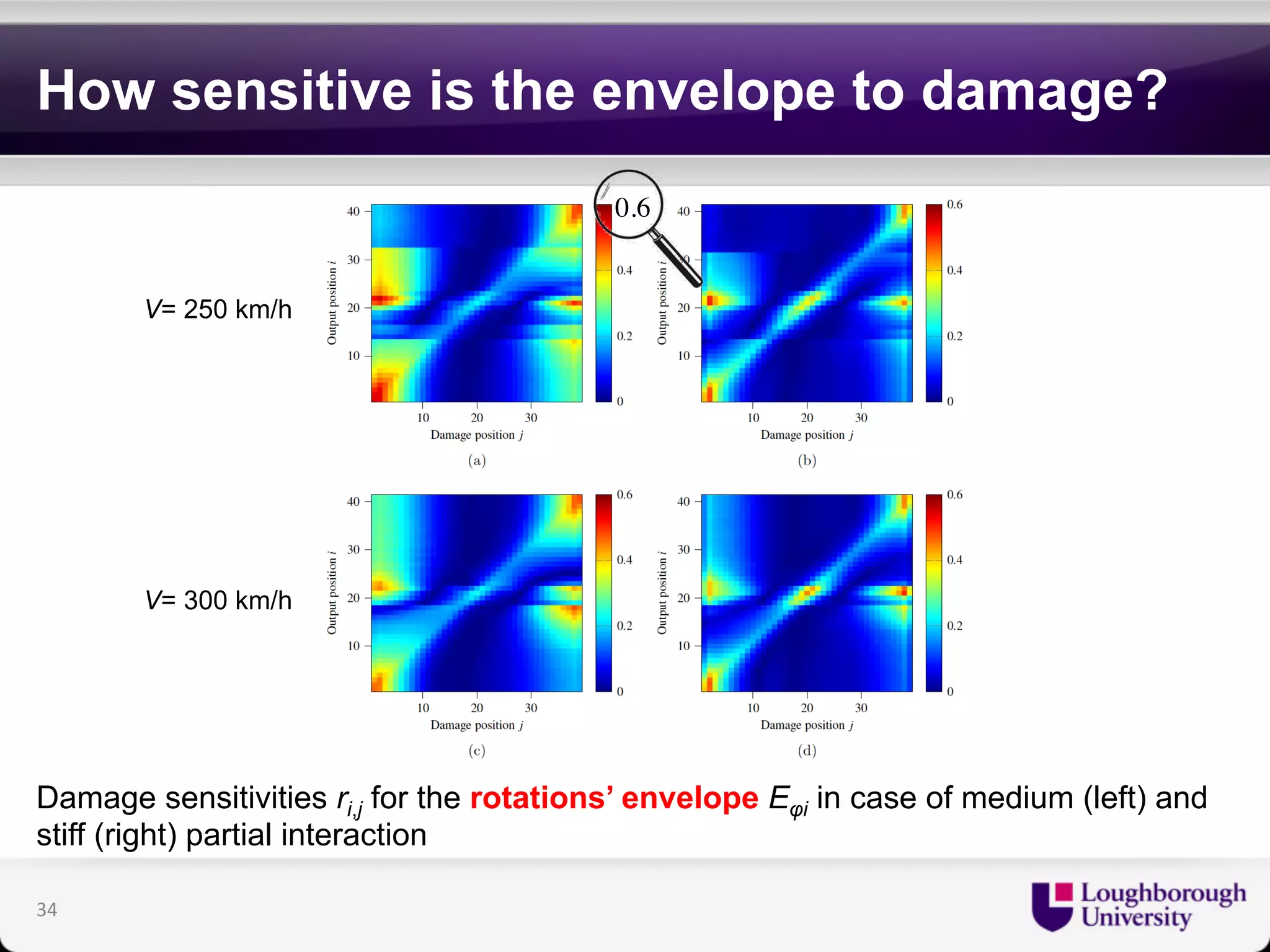
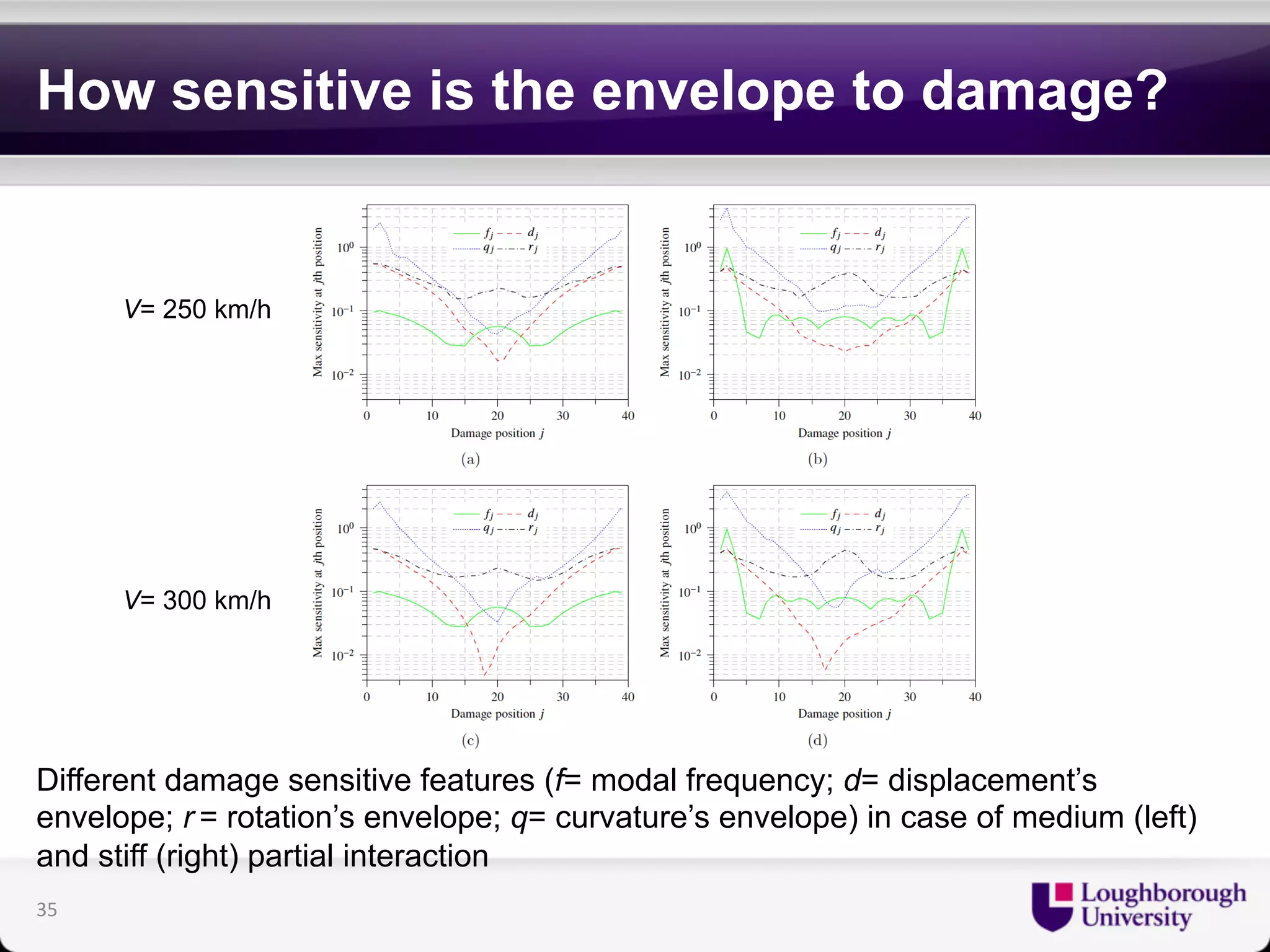
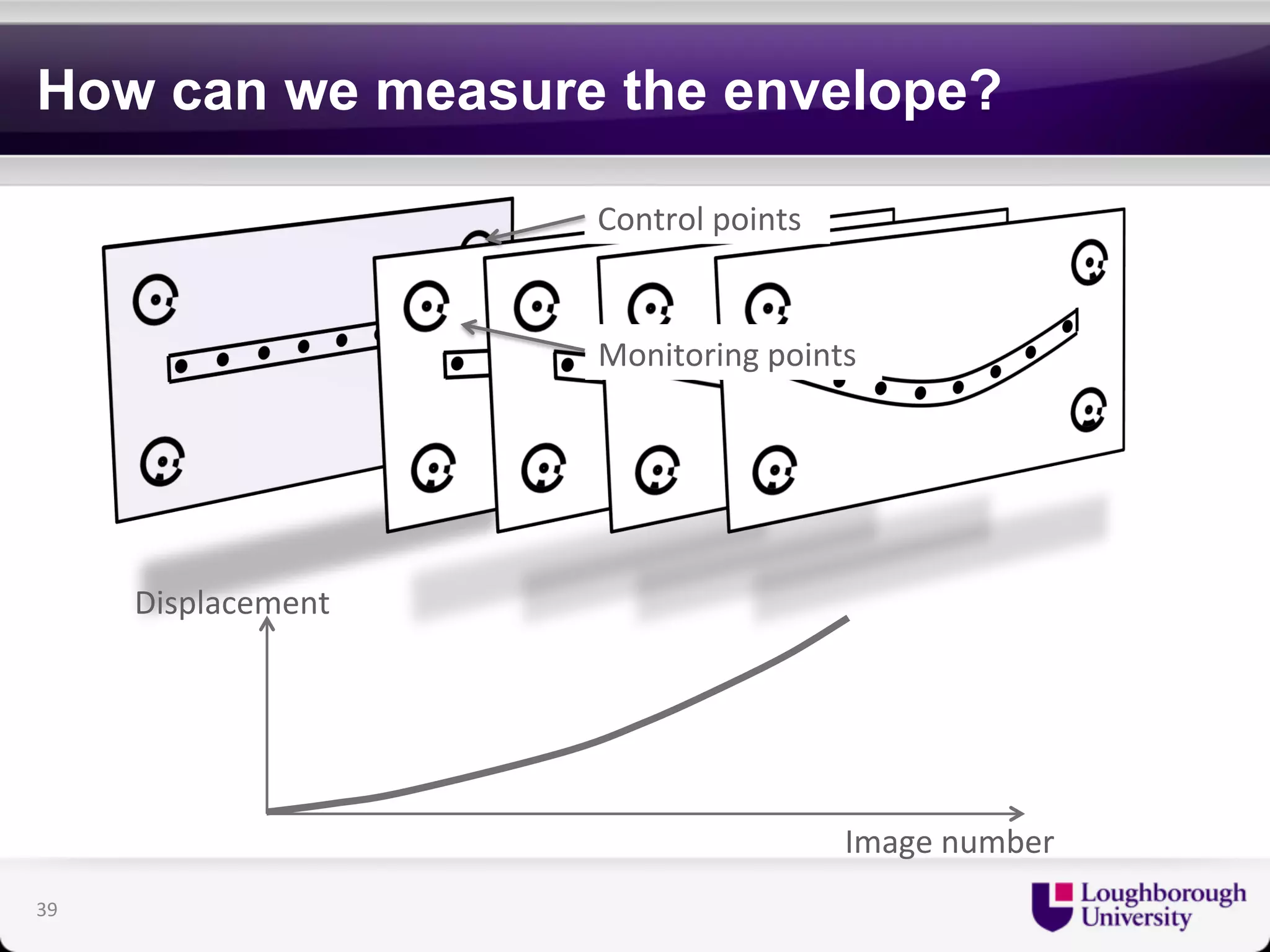
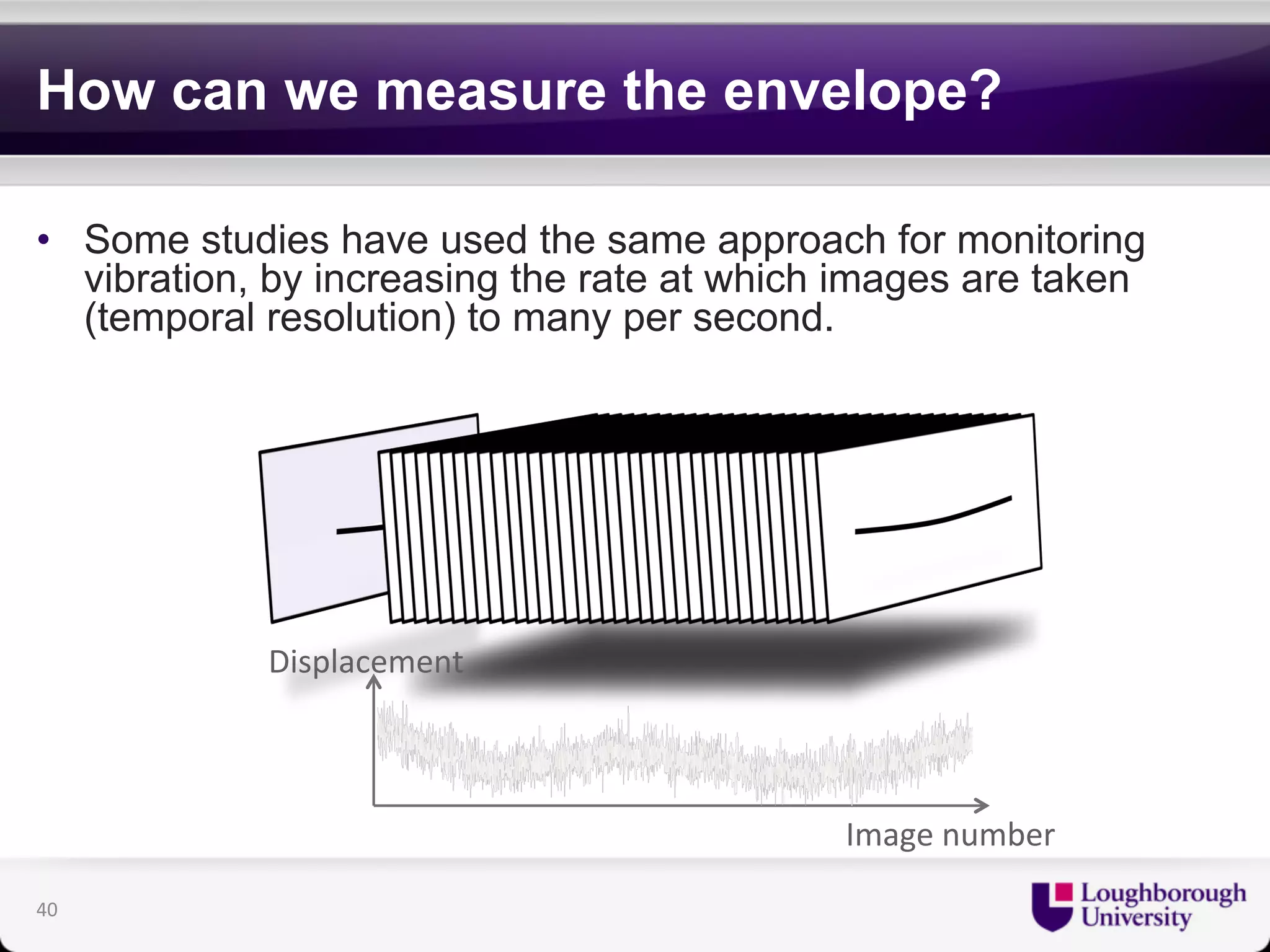
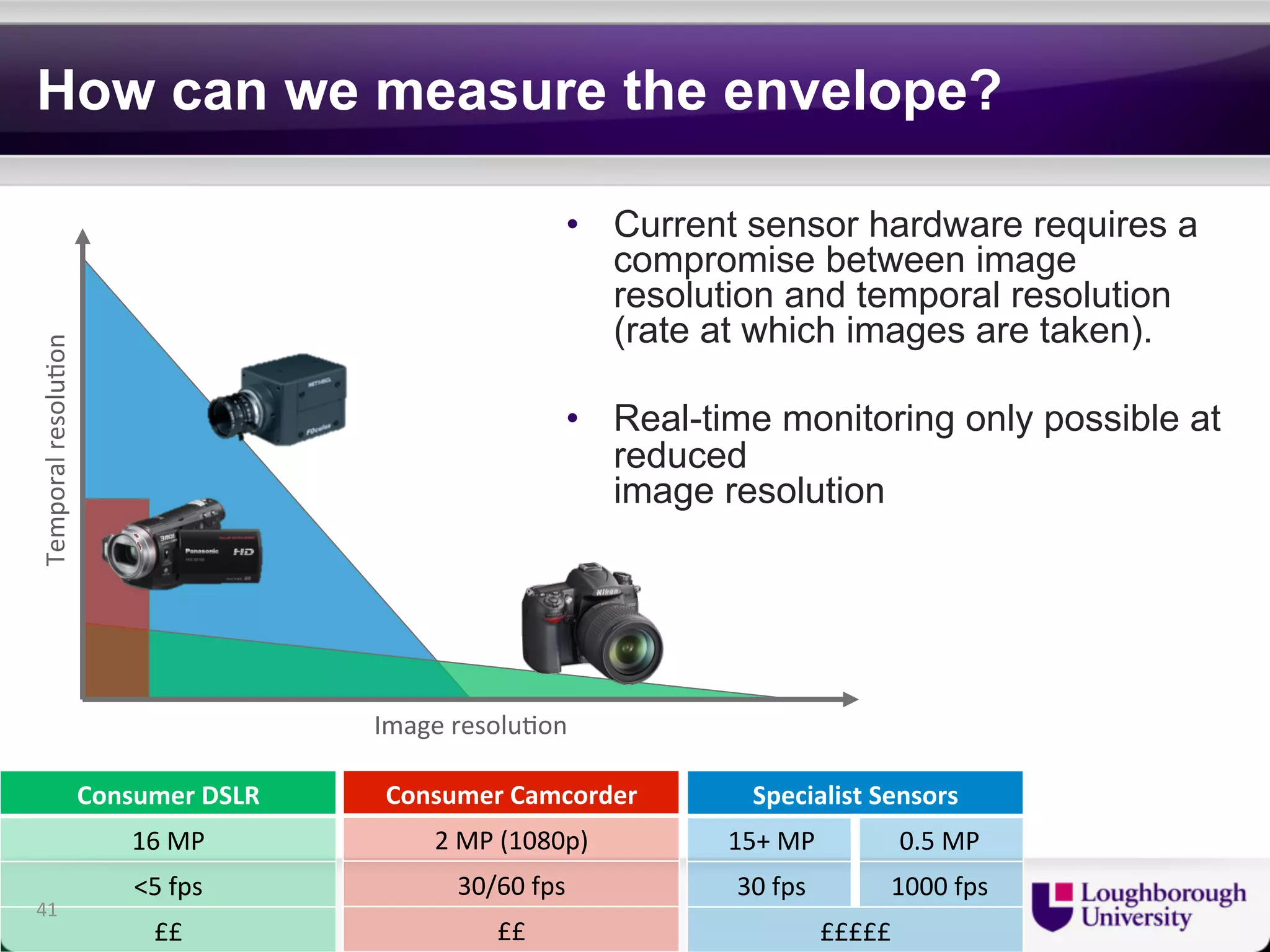
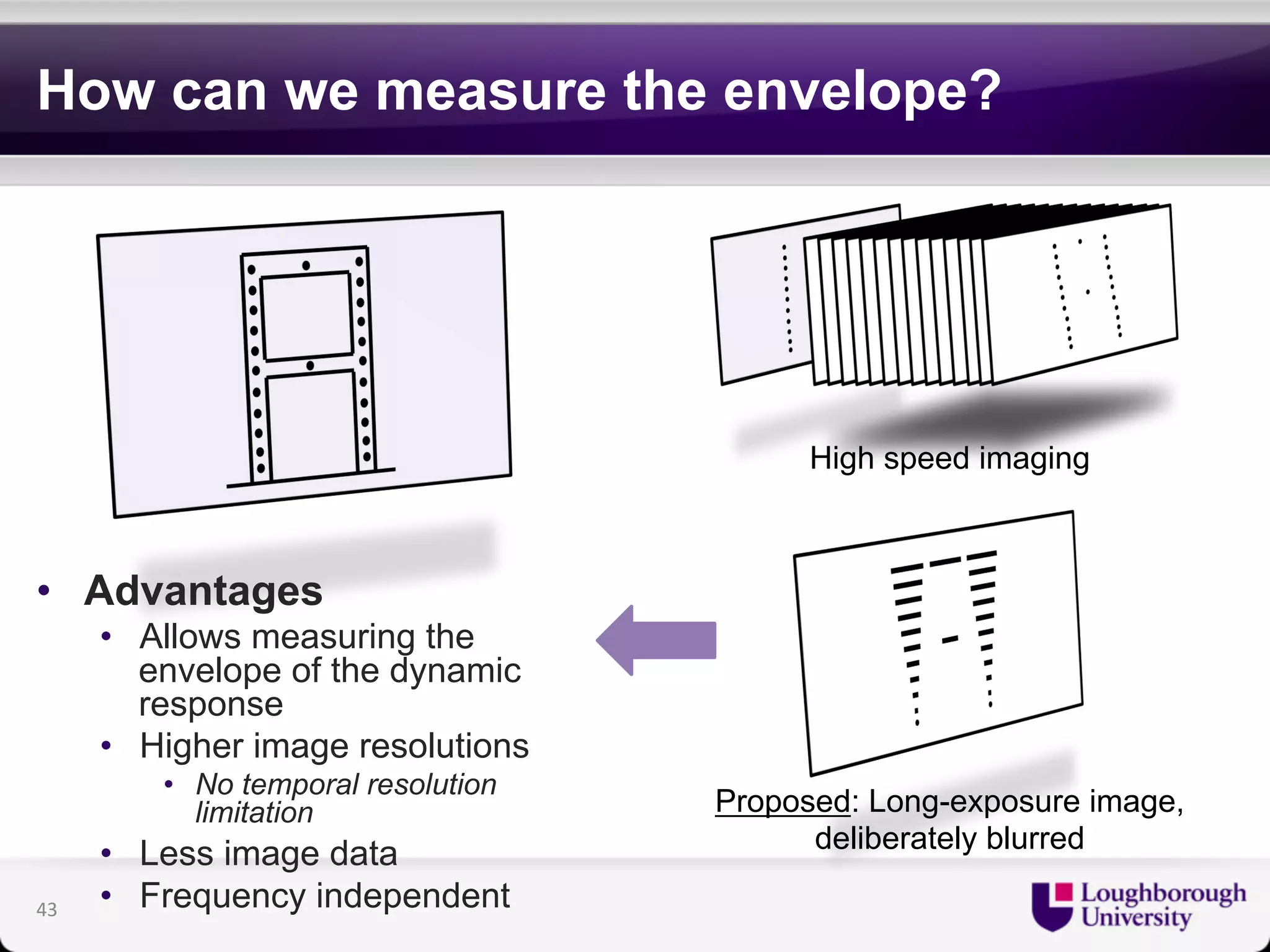
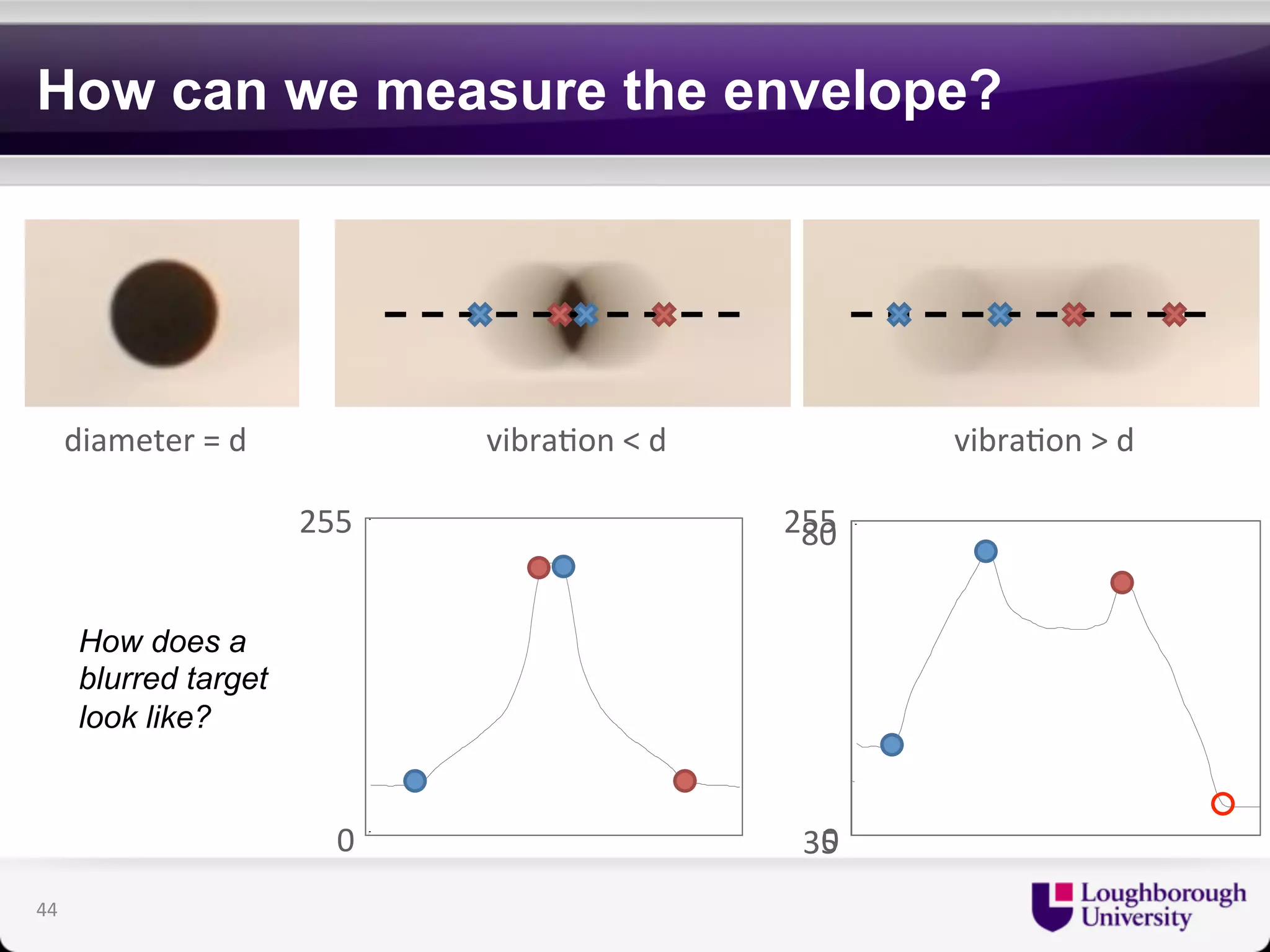
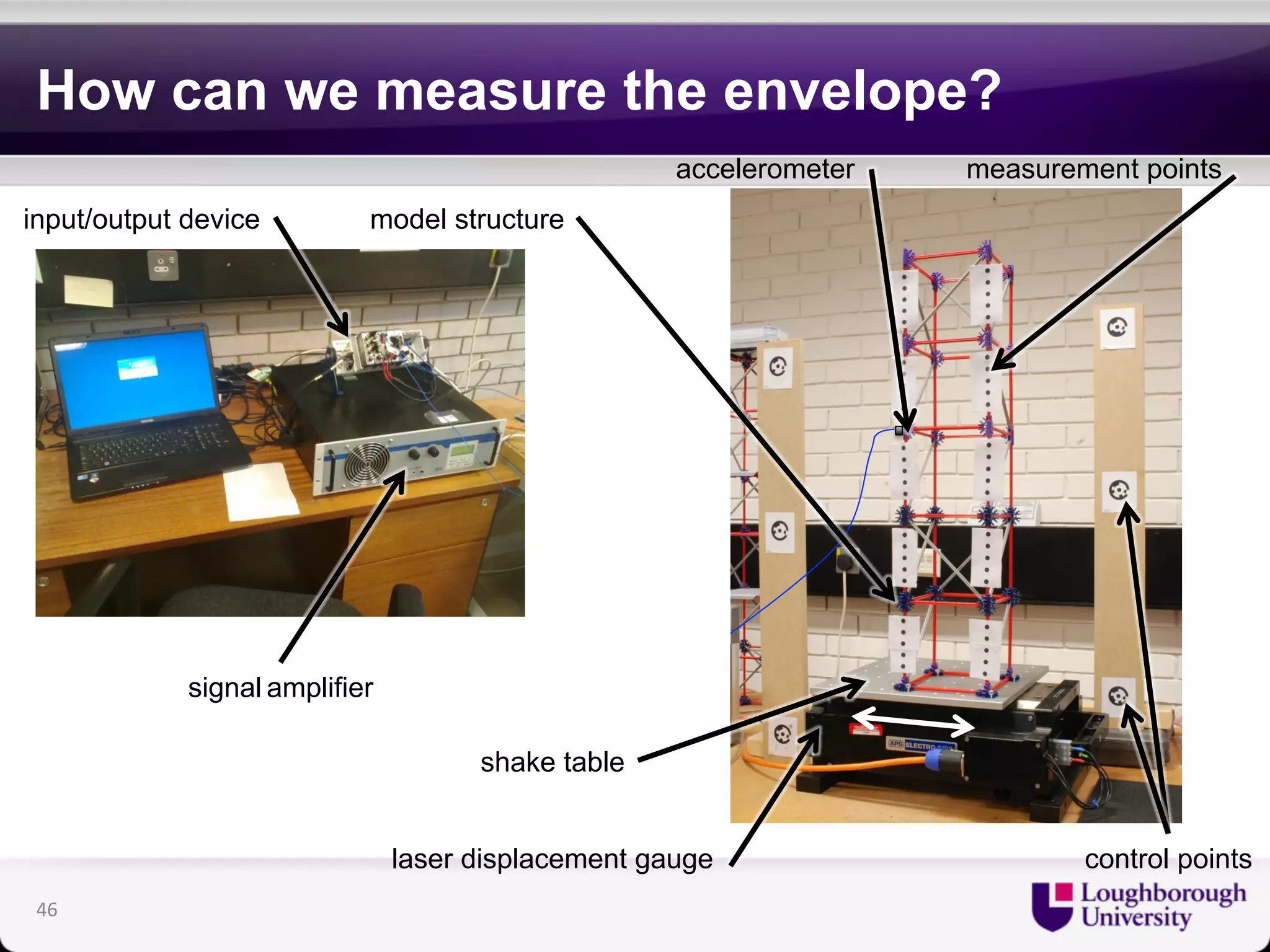
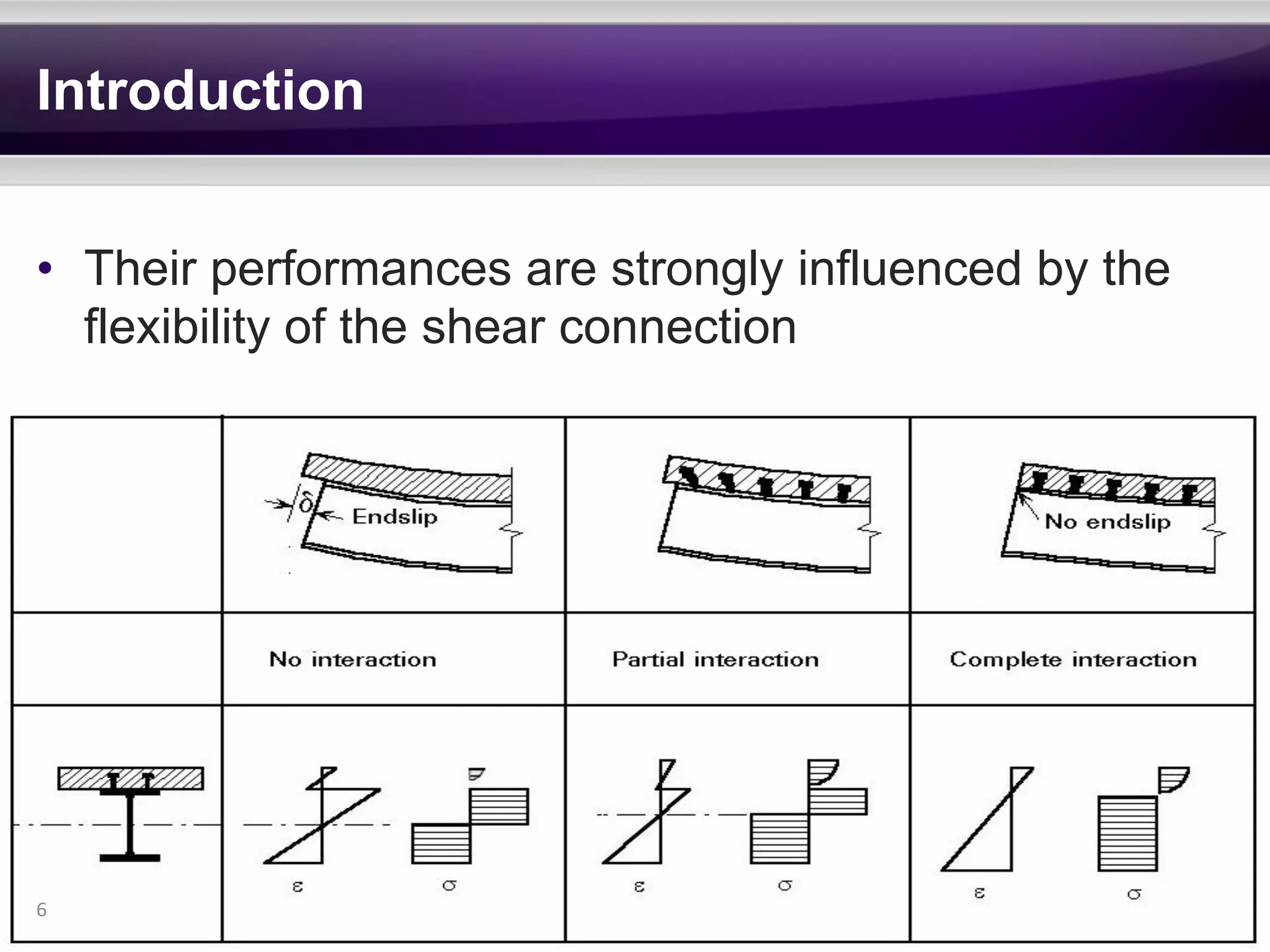
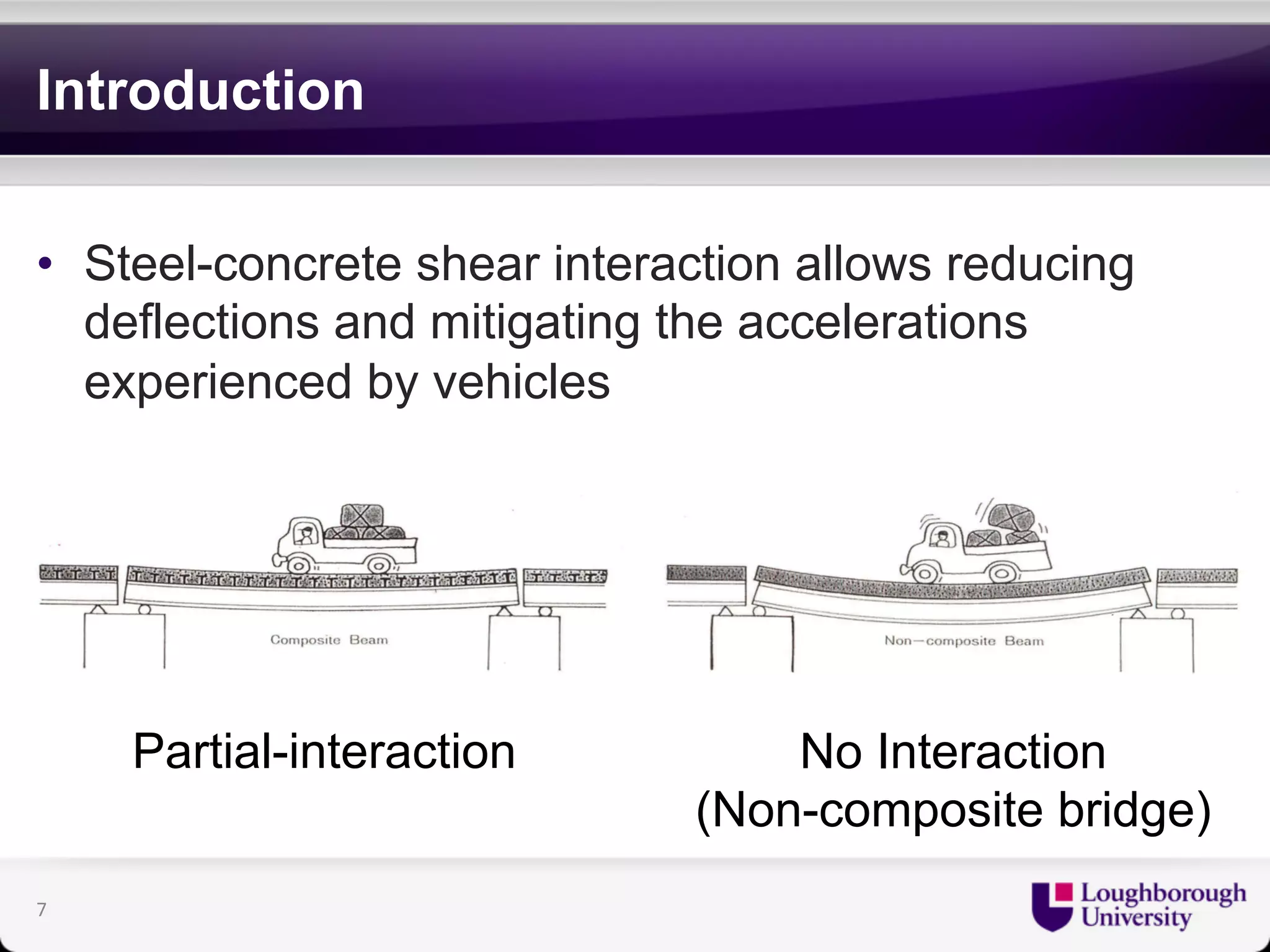
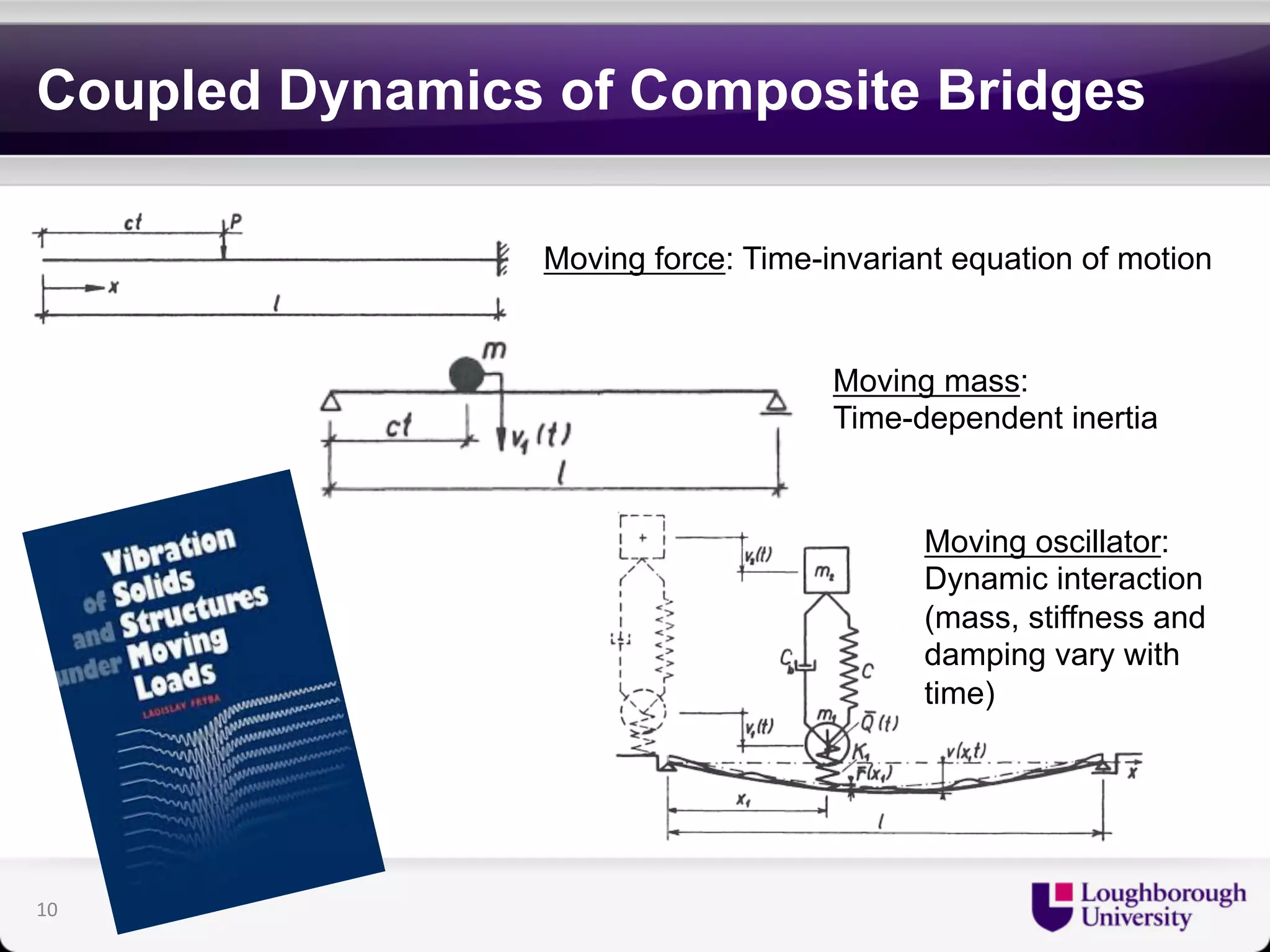
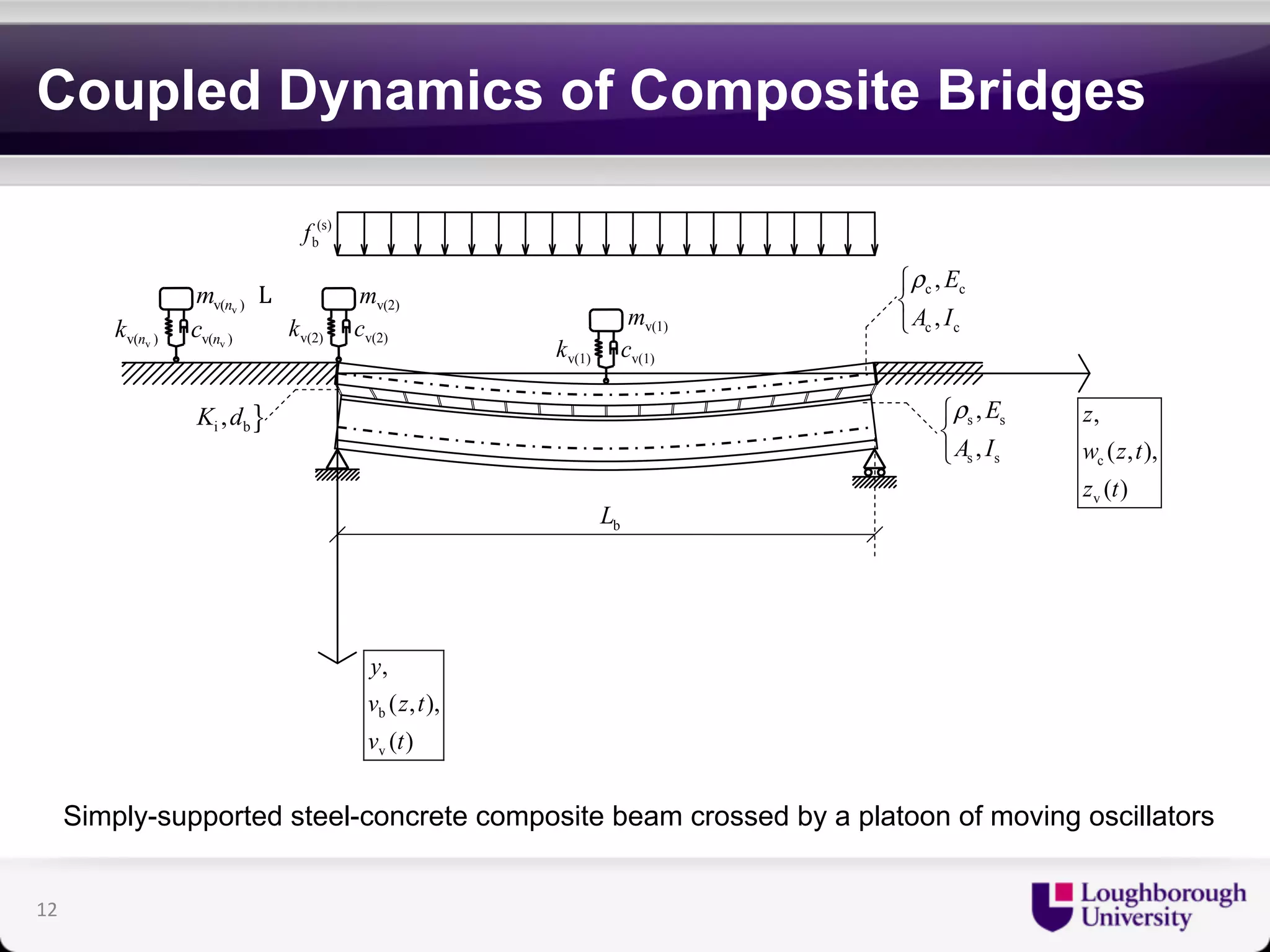
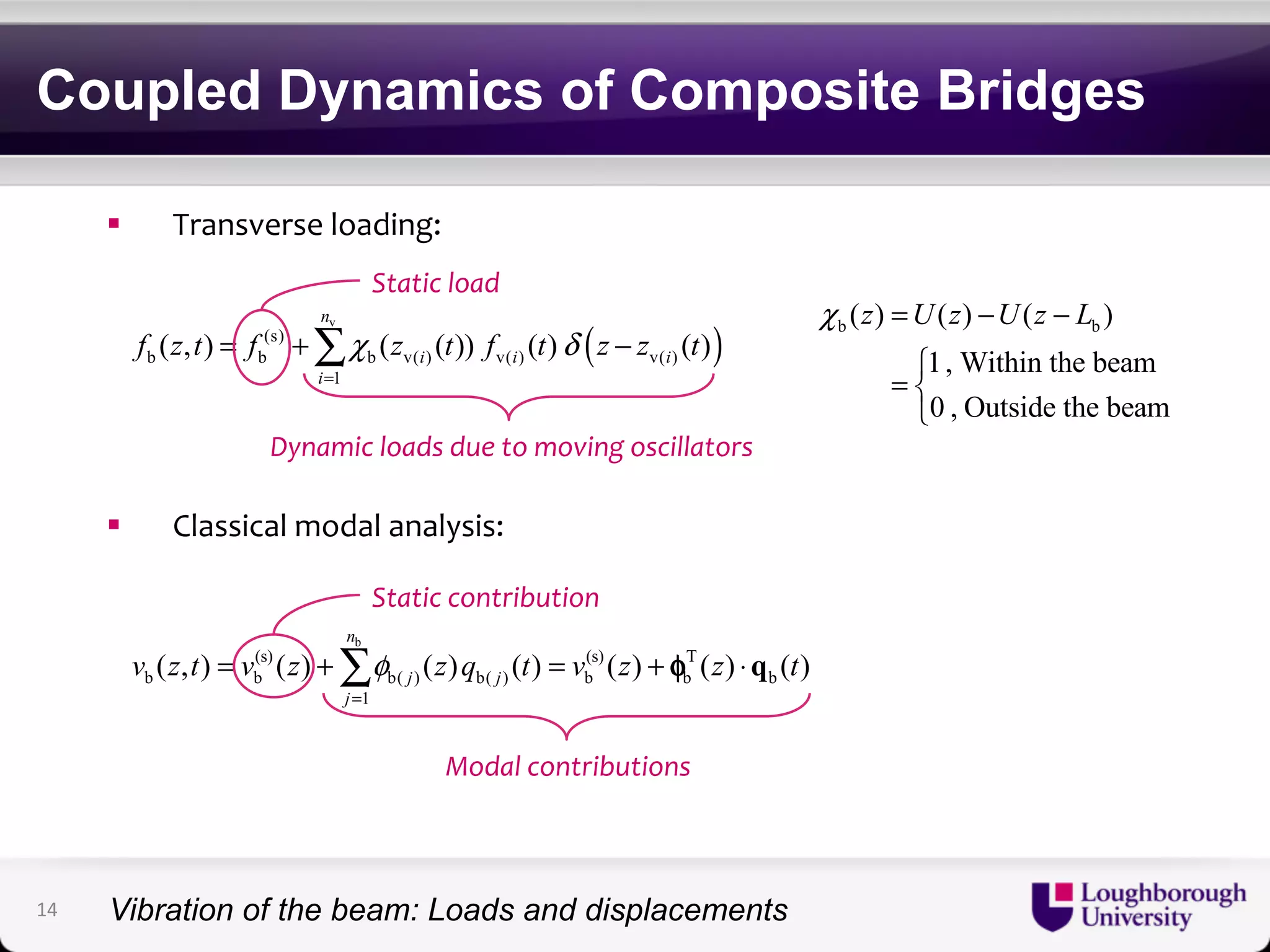
The document discusses research on the coupled dynamics of composite bridges, focusing on the effects of shear connections between steel and concrete components on bridge performance. It covers various analytical, numerical, and experimental studies addressing damage sensitivity and measurement methods. Key topics include dynamic interactions under moving forces, state-space representations of motion, and implications for structural health monitoring.

1. Using blurred images to assess
damage in bridge structures?
Dr Alessandro Palmeri
The School of Civil and Building Engineering
Loughborough University, UK
Email: A.Palmeri@LBORO.ac.uk
1

2. Research Mind Map
Structural
Dynamics
Stochastic
Mechanics
Seismic Analysis
and Design
Wind
Engineering
Isolators and
Dampers
Train-Bridge
Interaction
Random
Vibration
Performance-
Based Design
Design Assisted
by Testing
Random
Composites
Fast Dynamics
(Blast Loading)
Structural Health
Monitoring
2

3. Research Word Cloud (2000-date)
3
University of
Messina
2000-07
University of
Naples
Federico II
2001
University of
California at
Berkeley
2002
University of
Patras
2004
University of
Bradford
2008-09
Loughborough
University
2010-date

4. Outline
• Introduction
• 1. Coupled dynamics of composite bridges
(Analytical formulation, 2009-10)
• 2. How sensitive is the envelope to damage?
(Numerical study, 2012-13)
• 3. How can we measure the envelope?
(Experimental investigations, 2011-14)
• Conclusions
4

5. Introduction
• Composite steel-concrete
beams are
widely used in bridge
engineering
5

6. Introduction
• Their performances are strongly influenced by the
flexibility of the shear connection
6

7. Introduction
• Steel-concrete shear interaction allows reducing
deflections and mitigating the accelerations
experienced by vehicles
Partial-interaction No Interaction
(Non-composite bridge)
7

8. Analytical formulation,
2009-10
Coupled Dynamics of
Composite Bridges
8

9. Coupled Dynamics of Composite Bridges
• Literature Review
• The most popular approach for the mechanics of
composite steel-concrete beam is due to Newmark et al.
(1951), in which top slab and bottom girder are two beams
continuously connected by a linear-elastic interface
However…
• Non-rigid steel-concrete connection is ignored in the
technical literature devoted to the coupled vibrations of
bridges and vehicles
9

10. Coupled Dynamics of Composite Bridges
10
Moving force: Time-invariant equation of motion
Moving mass:
Time-dependent inertia
Moving oscillator:
Dynamic interaction
(mass, stiffness and
damping vary with
time)

11. Coupled Dynamics of Composite Bridges
• Computational Approach
• Higher-order partial differential equations of motion for
slender composite beams with partial interaction under a
platoon of moving oscillators are cast in a novel state-space
form with time-varying coefficients
• Time-independent modifications in inertia and rigidity due to partial
interaction between concrete and steel
• Time-dependent modifications due to the dynamic interaction
between composite beam and moving oscillators
Palmeri, 10th Int Conf on Rec Adv in Struct Dyn (RASD), 2010
11

12. Coupled Dynamics of Composite Bridges
v(1) v(nv ) mv(2) m m L
k
c
k c
v(nv ) v(nv ) v(2) v(2) k c v(1) v(1) (s)
b f
b L
E
A I
E
A I
,
,
ρ ⎧⎨⎩
,
,
s s
s s
ρ ⎧⎨⎩
c c
c c
} i b K ,d
z
w z t
z t
,
( , ),
c
( )
v
y
v z t
v t
,
( , ),
( )
b
v
Figure
1.
Simply-­‐supported
steel-­‐concrete
composite
beam
crossed
by
a
platoon
of
moving
oscillators.
Simply-supported steel-concrete composite beam crossed by a platoon of moving oscillators
12

13. Coupled Dynamics of Composite Bridges
! Cascade'equations'of'motion:'
⎪⎪⎨⎪
⎧ ⎧ ∂ 2 ⎫ ∂ 2 ⎧ ∂ 2 ⎫ ∂ 4 ⎧ ∂ 2
⎫ ⎪ ⎨ − + ∂ ⎬ ∂ ⎨ − ⎬ + = ∂ ∂ ⎨ − ∂ ⎬ ⎩ ⎭ ⎩ ⎭ ⎩ ⎭ ⎪∂ ⎛ ∂ ∂ ∂ ⎞ = ⎜ + − − ⎩⎪ ∂ ⎝ ∂ ∂ ∂ ⎟ ⎠
A v z t EI v z t R z t f z t
1 1 ( , ) 1 1 ( , ) ( , ) 1 1 ( , ) ,
b 2 2 2 b( ) 2 2 4 b 2 2 b
z t z z z
b b b
w z t f z t K d v z t A v z t EI v z t
z rEA z t z
( , ) 1 ( , ) ( , ) ( , ) ( , ) ;
! where:'
b b
f A A Agρ = ρ +ρ +
[ ]
[ ] [ ]
[ ]
(s)
b
b c c s s
EI E I E I
b(0) c c s s
EI EI E E A A d
c s c s 2
b( ) b(0) b
∞ E A E A
c c s s
= +
= +
+
Composite$beam$transverse$deflections$
2 2 4
[ ] [ ]
[ ]
[ ]
[ ]
[ ] [ ]
[ ]
2
2 i b
b
b(0)
b(0)
b( )
2
2 2 b(0) i b
b b
b( ) b(0)
b( )
b( )
1
;
1
K d
EI
EI
EI
EI K d
EI EI
EI
EI
α
β α
∞
∞
∞
∞
=
⎛ ⎞
⎜ − ⎟
⎜⎝ ⎟⎠
= =
⎛ ⎞
⎜ − ⎟
⎜⎝ ⎟⎠
Non$Composite$
Fully$Composite$
Concrete$slab$axial$displacements$
[ ] [ ]
[ ] [ ]
c 2
2 b i b 2 b b 2 b b(0) 4 b
b b c c
ρ
β α β
ρ
β
∞
13
Vibration of the beam: Governing equation

14. Coupled Dynamics of Composite Bridges
! Transverse(loading:(
n
Static(load(
( ) v
= (s)
+Σ −
f ( z , t ) f χ ( z ( t )) f ( t ) δ z z ( t
)
i i i
b b b v( ) v( ) v( )
=
1
i
Dynamic(loads(due(to(moving(oscillators(
! Classical(modal(analysis:(
χ z =U z −U z − L
b b ( ) ( ) ( )
1, Within the beam
0 , Outside the beam
⎧
=⎨⎩
b
= (s) +Σ = (s) + φ T
⋅q
v z t v z φ z q t v z z t
( , ) ( ) ( ) ( ) ( ) ( ) ( )
b b b( ) b( ) b b b
1
n
j j
j
=
Static(contribution(
Modal(contributions(
14
Vibration of the beam: Loads and displacements

15. Coupled Dynamics of Composite Bridges
! Modal&equations&of&motion:&
2 ⋅qb (t) = Jb ⋅Qb (t)
qb (t) + Ξb ⋅ qb (t) +Ωb
⎧ ⎫
( ) ( ( )) ( ) ( ( )) 1 ( ( ))
Q Σ φ φ
= ⎨ − ′′ ⎬
t χ z t f t z t z t
2 1 2
J = ⎡⎣I + Δm ⎤⎦ − b
1
b n bi
Ω J Ω k
b b b() bi
Ξ Ω
b b b 2ζ
−
∞ = ⎡⎣ ⋅ ⎡⎣ + Δ ⎤⎦⎤⎦
=
b( ) b( ,1) b( ,2) b( , b ) Diag n ω ω ω ∞ ∞ ∞ ∞ Ω = ⎡⎣ L ⎤⎦
[ ]
[ ]
2
⎛ ⎞ ∞
=⎜ ⎟
⎝ ⎠
b( )
b( )
b b
j
j EI
L A
ω π
ρ
1
⎡ ⎤
π
m N
Δ = bi 2 ⎢ b
⎥
[EI]
L
β
⎣ ⎦
b b
∞ ⎡ ⎤
k N
Δ = ⎢ ⎥
[ ]
2
6
b( )
π
bi 2 b
A L
α ρ
⎣ ⎦
b b b
[ ] b b N = Diag 1 2 L n
v
b b v( ) v( ) b v( ) 2 b v( )
1 b
n
i i i i
i
= β
⎩ ⎭
15
Vibration of the beam: Modal analysis

16. Coupled Dynamics of Composite Bridges
! Absolute)displacements)are)used:)
!Impulsive!terms!in!the!equations!of!motion!can!be!avoided!
)(Muscolino,)Palmeri)&)Sofi,)2009))
mv(i) vv(i) (t) = −cv(i)  vv(i) (t) −  vw(i) ( (t))− kv(i) vv(i) (t) − vw(i) ( (t)),
Static!contributions! Dynamic!contributions!
T (t) ⋅qb (t)
vw(i) (t) = rv(i) (t) + χ b (zv(i) (t))abv(i)
( T (t) ⋅ q(t) + bT (t) ⋅q(t))
b bv(i)
b  vw(i) (t) = sv(i) (t) + χ b (zv(i) (t)) abv(i)
16
Vibration of the oscillator: Governing equation

17. Coupled Dynamics of Composite Bridges
! Equations*of*motion:*
Mv ⋅ vv (t) +Cv ⋅ vv (t) +Kv ⋅ vv (t) = Cv ⋅sv (t) +Kv ⋅rv (t)
+Cvb ⋅ qb (t) + Kvb (t) + Lvb (t) ⎡⎣
⎤⎦
⋅qb (t)
⎡⎣⎢
Mv = Diag mv(1) mv(2)  mv(nv )
⎤⎦⎥
⎡⎣⎢
Cv = Diag cv(1) cv(2)  cv(nv )
⎤⎦⎥
T (t)
Cvb (t) = Cv ⋅Xv (t) ⋅Abv
⎡⎣⎢
Kv = Diag kv(1) kv(2)  kv(nv )
⎤⎦⎥
T (t)
Kvb (t) = Kv ⋅Xv (t) ⋅Abv
T (t)
Lvb (t) = Cv ⋅Xv (t) ⋅Bbv
Xv (t) = Diag χ b (zv(1) (t)) χ b (zv(2) (t))  χ b (zv(nv ) (t)) ⎡⎣⎢
⎤⎦⎥
Abv (t) = abv(1) (t) abv(2) (t)  abv(nv ) (t) ⎡⎣⎢
⎤⎦⎥
Bbv (t) = bbv(1) (t) bbv(2) (t)  bbv(nv ) (t) ⎡⎣⎢
⎤⎦⎥
17
Vibration of the oscillator: Matrix equations

18. Coupled Dynamics of Composite Bridges
! The$generic$oscillator/beam$interaction$force$is$given$by:$
fv(i) (t) = mv(i) g
( T ⋅qb (t))
+cv(i)  vv(i) (t) − sv(i) (t) − χ b (zv(i) (t))abv(i)
T ⋅qb ( (t))
$Leading$to:$
T ⋅ qb (t) − χ b (zv(i) (t))bbv(i)
+kv(i) vv(i) (t) − rv(i) (t) − χ b (zv(i) (t))abv(i)
qb (t) + Ξb + ΔCb (t) ⎡⎣
⎤⎦
2 + ΔKb (t) ⎡⎣
⋅ qb (t) + Ωb
⎤⎦
⋅qb (t)
= Cbv (t) ⋅ vv (t) +Kbv (t) ⋅ vv (t) +Q b (t)
ΔCb (t) = Tbv (t) ⋅Cvb (t)
ΔKb (t) = Tbv (t) ⋅ Kvb (t) + Lvb (t) ⎡⎣
⎤⎦
Cbv (t) = Tbv (t) ⋅C
Kbv (t) = Tbv (t) ⋅Kv
Q b (t) = Tbv (t) ⋅ gMv ⋅τ v −Cv ⋅sv (t) −Kv ⋅rv { (t)}
τ v = { 1 1  1 }T
Tbv (t) = Jb ⋅ Abv (t) + ΔAbv (t) ⎡⎣
⎤⎦
⋅Xv (t)
ΔAbv (t) = − 1
2 φ ′′ b (zv(1) (t)) φ ′′ b (zv(2) (t))  φ ′′ b (zv(nv ) (t)) ⎡⎣⎢
βb
⎤⎦⎥
18
Vibration of the oscillator: Matrix equations

19. Coupled Dynamics of Composite Bridges
! Matrix'equations'of'motion'can'be'obtained'for'the'platoon'of'
moving'oscillators:'
2 ⋅qv (t) = Q v + μv ⋅Cvb ⋅ qb (t) + μv ⋅ Kvb (t) + Lvb (t) ⎡⎣
qv (t) + Ξv ⋅ qv (t) +Ωv
⎤⎦
⋅qb (t)
{ } μ = M− b
v v(1) v(2) v( ) ( ) ( ) ( ) ( ) n q t = q t q t L q t Dimensional*
⎡⎣⎢
Ξv = 2Diag ζ v(1) ζ v(2)  ζ v(nv )
⎤⎦⎥
⋅Ωv
⎡⎣⎢
Ωv = Diag ωv(1) ωv(2)  ωv(nv )
⎤⎦⎥
Q v (t) = μv ⋅ Cv ⋅sv (t) +Kv ⋅rv { (t)}
i
v( )
v( )
v( )
v( )
v( )
v( ) v( ) 2
i
i
i
i
i i
k
m
c
m
ω
ζ
ω
=
=
1 2
v v
T
consistency*
19
Coupled vibration

20. Coupled Dynamics of Composite Bridges
! Finally'the'two'matrix'equations'are'rewritten'in'an'enlarged'
modal'space:'
q(t) + c0 + Δc(t) ⎡⎣
⎤⎦
⋅ q(t) + k0 + Δk(t) ⎡⎣
⎤⎦
⋅q(t) = Q(t)
O
⎡ = ⎢ n v ×
n
⎤
b
⎥
⎢⎣ b v
⎥⎦
O C
⎡ − ⋅ ⎤
v v
v
c 0
O
b
v vb
bv v b
( )
( )
( ) ( )
n n
n n t
t
t t
×
×
c
Δ = ⎢⎣− ⎢ C ⋅ Δ C
⎥ ⎥⎦
Ξ
Ξ
μ
μ
T (t) Q b
{ T (t) }T
v b
b v
O
O
[ ]
O K L
v v
2
v
0 2
b
( ) ( )
v vb vb
k
μ
bv v b
( )
( ) ( )
n n
n n
n n t t
t
t t
×
×
×
⎡ Ω ⎤
= ⎢ ⎥
⎢ Ω ⎥ ⎣ ⎦
⎡ − ⋅ + ⎤
Δ =⎢ ⎥
⎢⎣− ⋅ Δ ⎥⎦
k
K μ
K
{ T T }T
v b q(t) = q (t) q (t) Q(t) = Q v
“Small”'modifications'
20
Coupled vibration: Proposed model

21. Coupled Dynamics of Composite Bridges
! Single'step+(unconditionally+stable)+numerical+integration:+
{[ ] [ ] [ ] } 0 01 01 02 x(t + Δt) = E(t) ⋅ Θ + Γ ⋅ΔD(t) ⋅ x(t) + Γ ⋅V ⋅Q(t) + Γ ⋅V ⋅Q(t + Δt)
! Reference+transition+matrix+without+dynamic+interaction:+
L I D
Γ Θ
! Dynamic+modification+matrix:+
= ⎡⎣ Θ
− n +
n
⎤⎦ ⋅
−
= ⎡ − ⎤ ⎢⎣ Δ ⎥⎦
⋅ = ⎡ ⎤ ⎢⎣− Δ ⎥⎦
⋅ 0 0 2( ) 0
v b
1
−
L D
01 0 0 0
1
L I D
n n
t
−
+
02 0 2( ) 0
v b
1
1
1
t
2( ) 02 ( ) ( ) n n t t t −
v b
1
+ E = ⎡⎣Ι − Γ ⋅ΔD + Δ ⎤⎦
Γ
[ ] 0 0 Θ = exp D Δt
21
Coupled vibration: Proposed numerical scheme

22. Coupled Dynamics of Composite Bridges
Time histories of beam’s transverse deflection at midspan for different levels of partial interaction
22

23. Coupled Dynamics of Composite Bridges
Time histories of oscillator’s absolute acceleration for different levels of partial interaction
23

24. Part-1 Conclusions (from 2010)
• A novel method of dynamic analysis has been proposed and
numerically validated for studying the dynamic interaction
phenomenon in composite steel-concrete beams subjected to a
platoon of single-DoF moving oscillators
• Time-independent modifications arise in the composite beam because of the
partial interaction between concrete slab and steel girder
• Beam-oscillators dynamic interaction is represented by a set of time-dependent
functions, playing the role of time-varying stiffness and damping
coefficients
• A single-step numerical scheme of solution has been formulated,
based on the observation that the dynamic modifications are small
• Further studies:
• Effect of roughness in the beam-oscillators’ contact
• Sensitivity of the dynamic response of the subsystems to the degree of PI in
the supporting beam
24

25. Part-1 Conclusions
Bending Moment M Shear Force V
Mean value μ (top) and standard deviation σ (bottom) of the internal forces M and V due to a
single moving oscillator at midspan of a simply-supported solid beam with rough surface
Muscolino, Palmeri & Sofi, 10th Int Conf on Struct Safety & Reliability (ICOSSAR), 2009
25

26. Numerical study,
2012-13
How sensitive is the
envelope to damage?
26

27. How sensitive is the envelope to damage?
• Literature Review
• Conventional approaches of damage detection (including ultrasonic, thermal, eddy
current and X-ray testing) were termed as cumbersome and expensive
• Vibration-based damage methods have emerged, as they allow identifying meaningful
changes in the dynamic characteristics of the composite beam
• Accelerometers have been extensively employed, BUT their application to large structural
systems may be difficult because of long cabling, number of sensors and installation time
• Laser doppler vibrometers can be used as a viable non-contact alternative, especially when
targets are difficult to access, BUT the simultaneous acquisition of vibration at multiple points
would make very expensive the dynamic testing
Therefore…
• The idea of using the envelopes profile of deflections and rotations induced by a moving
load has been investigated
• That’s radically different than recording and analysing multiple time histories
Kasinos, Palmeri & Lombardo, Structures, In press
27

28. How sensitive is the envelope to damage?
• Key Assumptions
1. Linear-elastic constitutive law
2. Finite element model built with SAP2000, using:
• Beam elements for top concrete slab and bottom steel girder
• Elastic springs for the shear connectors
3. Planar motion (no twisting moment)
4. Moving force F (massless) with constant velocity V
5. Damage simulated as stiffness reduction in the shear springs
28
Application
Programming
Interface

29. How sensitive is the envelope to damage?
• Governing equations
• Dynamic response of interest (displacement
or rotation)
• Envelope of the dynamic response
• Damage measure (DM)
29

30. How sensitive is the envelope to damage?
Dynamic amplification factors of midspan deflection δM and right support rotation φR
for different levels of concrete-steel partial interaction
= θ due to gravitational loads
= θ when the
moving force is
applied statically
Amplification factors:
30

31. How sensitive is the envelope to damage?
Normalised envelope of midspan deflection δM and right support rotation φR for
different levels of concrete-steel partial interaction
31

32. How sensitive is the envelope to damage?
Damage sensitivities fi,j for the natural frequencies associated with the first six
flexural modes of vibration in case of medium (left) and stiff (right) partial interaction
32

33. How sensitive is the envelope to damage?
V= 250 km/h
V= 300 km/h
Damage sensitivities di,j for the displacements’ envelope Eδi in case of medium (left)
and stiff (right) partial interaction
33
0.6

34. How sensitive is the envelope to damage?
V= 250 km/h
V= 300 km/h
Damage sensitivities ri,j for the rotations’ envelope Eφi in case of medium (left) and
stiff (right) partial interaction
34
0.6

35. How sensitive is the envelope to damage?
V= 250 km/h
V= 300 km/h
Different damage sensitive features (f= modal frequency; d= displacement’s
envelope; r = rotation’s envelope; q= curvature’s envelope) in case of medium (left)
and stiff (right) partial interaction
35

36. Part-2 Conclusions
• The envelope of deflections and rotations induced by moving
loads has been suggested as damage sensitive feature for
composite steel-concrete bridges
• The envelope of the dynamic response tends to increase when
damage occurs in the shear connectors
• The envelope enjoys:
• High sensitivity to the damage (higher than frequency shifts, at least
for the first few modes of vibration)
• The sensitivity tends to increase closer to the ends of the bridge, where
damage in the shear connectors is more likely to happen
• Ordered sets of results, that can potentially enhance the
predictiveness of damage-detection algorithms
36

37. Experimental investigations,
2011-14
How can we measure
the envelope?
37

38. How can we measure the envelope?
• Literature Review
• Advantages of
photogrammetric
monitoring techniques
includes:
• Simultaneous measurement
of many points
• Non-contact
• Small and inexpensive
targets
• Relatively less expensive
• Scalable
Ronnholm et al., The Photogrammetric
Record, 2009
Albert et al., 2nd Symposium on Geodesy for
Geotechnical and Structural Engineering,
2002 38

39. How can we measure the envelope?
Control
points
Monitoring
points
39
Displacement
Image
number

40. How can we measure the envelope?
• Some studies have used the same approach for monitoring
vibration, by increasing the rate at which images are taken
(temporal resolution) to many per second.
Displacement
Image
number
40

41. How can we measure the envelope?
• Current sensor hardware requires a
compromise between image
resolution and temporal resolution
(rate at which images are taken).
• Real-time monitoring only possible at
reduced
image resolution
Image
resolu?on
Temporal
resolu?on
Consumer)DSLR)
16#MP#
<5#fps#
££#
Consumer)Camcorder)
2"MP"(1080p)"
30/60"fps"
££"
Specialist*Sensors*
15+$MP$ 0.5$MP$
30$fps$ 1000$fps$
£££££$
41

42. How can we measure the envelope?
• Literature Review
Vehicle speed
Measuring motion
of sports balls
Caglioti & Giusti,
Computer Vision and
Image Understanding,
2009
Blurred images for…
detection
Lin, Li, & Chang, Image and
Vision Computing, 2008
Measuring vibration
of computer circuits
Wang et al., Pattern
Recognition Letters, 2007
42
Spacecraft
guidance systems
Xiaojuan & Xinlong, Acta
Astronautica, 2011

43. How can we measure the envelope?
High speed imaging
Proposed: Long-exposure image,
deliberately blurred
• Advantages
• Allows measuring the
envelope of the dynamic
response
• Higher image resolutions
• No temporal resolution
limitation
• Less image data
• Frequency independent 43

44. How can we measure the envelope?
diameter
=
d
vibra?on
<
d
vibra?on
>
d
255
80
80
250
75
70
200
65
60
150
55
50
100
45
50
40
35
0
0
35
30
255
250
200
150
100
50
0
0
How does a
blurred target
look like?
44

45. How can we measure the envelope?
Accuracy ≅ 1 pixel Sub-pixel accuracy
45

46. How can we measure the envelope?
model structure
shake table
accelerometer measurement points
control points
input/output device
signal amplifier
laser displacement gauge
46

47. How can we measure the envelope?
1st Mode: 5 Hz 2nd Mode: 8 Hz 3rd Mode: 12 Hz
5 Hz
• 50 points/image
• horizontal scale x15
47

48. How can we measure the envelope?
110 120 130 140 150 160 170
25
20
15
10
5
0
-5
-10
-15
-20
Displacement (mm)
Time (s)
• Full-scale case study
• Wilford bridge, Nottingham
• ~70m span suspension footbridge
Laser Doppler vibrometer
(courtesy of Polytec Ltd)
Proposed image processing
48

49. How can we measure the envelope?
1st mode (5 Hz) 2nd mode (8 Hz) 3rd mode (12 Hz)
0.2
0.4
0.6
0.2
0.4
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
y x
z
0.2
0.4
0.6
0.2
0.4
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
y x
z
0.2
0.4
0.6
0.2
0.4
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
y x
z
Modification 2 (c) Modification 1 (b) Unmodified structure (a)
0.5
0.6 0.7 0.8
0
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0.2
y x
z
0.5
0.6
0.7
0.8
0
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0.2
y x
z
0.5
0.6
0.7
0.8
0
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.2
0.1
y x
z
0.5 0.6 0.7 0.8
0
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.2
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.2
0.1
x
z
y
0.5 0.6 0.7 0.8
0
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.2
0.1
y x
z
0.5 0.6 0.7 0.8
0
0.1
y x
z
Unmodified Modification 1 Modification 2
• 3D effects of structural
modifications
Added mass
Standard member
Reduced stiffness member
(back of model)
49

50. Part-3 Conclusions
• Novel approach to identifying vibration patterns in civil engineering
structures using long-exposure images
• Targets appear blurred because of the motion of the structure
• The vibration envelope is recorded, not the instantaneous deformed shapes
• Sensors with higher image resolutions can be used
• High-quantity measurements achieved in both laboratory and field tests
• The approach can also be used to detect structural changes
• The proposed frequency-independent approach expands the capabilities of
existing sensors
• Otherwise restricted by their imaging frequency
McCarthy, Chandler & Palmeri, Photogrammetric Record, Under review
50

51. Final Remarks
• Part-1: Concrete-steel partial interaction and vehicle-bridge
dynamic interaction can be represented
efficiently with the proposed analytical formulation for
the dynamics of composite bridges
• Part-2: A numerical study has shown a promising
level of sensitivity to damage for the envelope of the
dynamic response of composite bridges subjected to
moving loads
• Part 3: Experimental investigations have confirmed
that long-exposure digital images can be used to
measure the envelope of 2D and 3D structural
vibrations with good accuracy (sub-pixel)
51

52. Acknowledgments
52
Stavros Kasinos
Loughborough University
Dr Mariateresa Lombardo
Loughborough University
David McCarthy
Loughborough University
Prof Jim Chandler
Loughborough University

53. References
• J Albert, HG. Maas, A Schade & W Schwarz, Pilot studies on photogrammetric bridge deformation
measurement, 2nd Symp on Geodesy for Geotechnical and Structural Engineering, Berlin, May 2002
• L Frýba, Vibration of Solids and Structures Under Moving Loads, 3rd Ed., Thomas Telford,1999
• S Kasinos, A Palmeri & M Lombardo, Using the vibration envelope as damage-sensitive feature in
composite beam structures, Structures, In press
• DMJ McCarthy, JH Chandler & A Palmeri, Monitoring dynamic structural tests using image deblurring
techniques, 10th Int Conf on Damage Assessment of Structures, Dublin, July 2013
• DMJ McCarthy, JH Chandler & A Palmeri, Monitoring 3D vibrations in structures using high resolution
blurred imagery, The Photogrammetric Record, Under review
• G Muscolino, A Palmeri & A Sofi, Absolute versus relative formulations of the moving oscillator problem,
Int Journal of Solids and Structures 46: 1085-1094, 2009
• G Muscolino, A Palmeri & A Sofi, Random fluctuation of internal forces in rough beams under moving
oscillators, 10th Int Conf on Structural Safety and Reliability, Osaka, September 2009
• NM Newmark, CP Siess & IM Viest, Test and analysis of composite beams with incomplete interaction.
Proc of the Society of Experimental Stress Analysis 9: 75-92, 1951
• A Palmeri, Vibration of slender composite beams with flexible shear connection under moving oscillators,
10th Int Conf on Recent Advances in Structural Dynamics, Southampton, July 2010
• P Rönnholm, Comparison of measurement techniques and static theory applied to concrete beam
deformation, The Photogrammetric Record, 24: 351-371
53