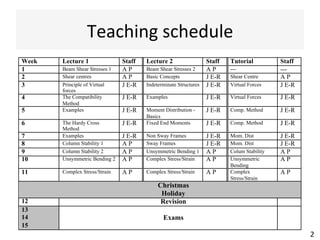
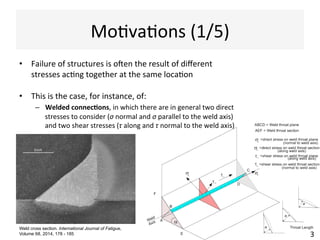
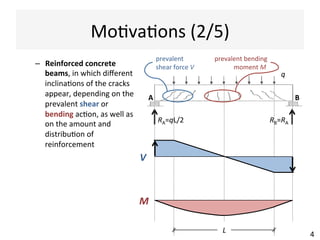
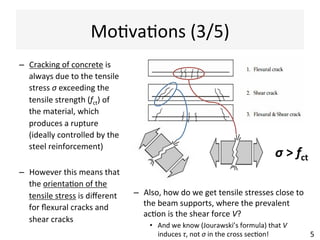
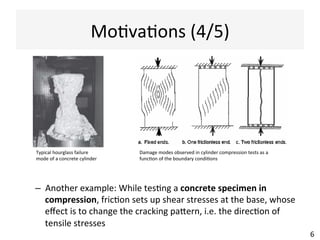
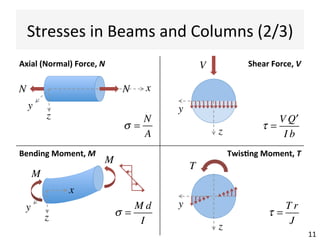
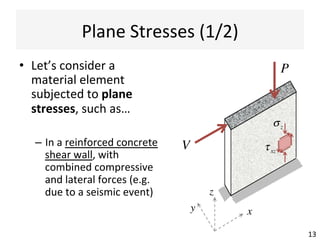
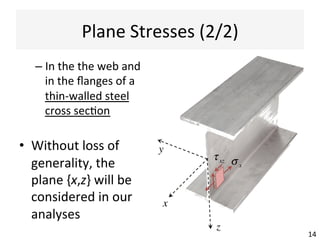
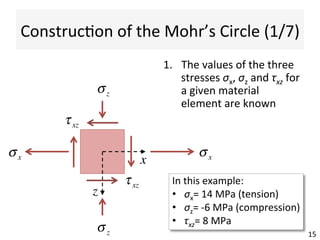
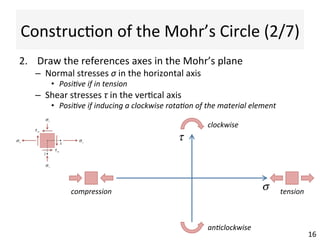
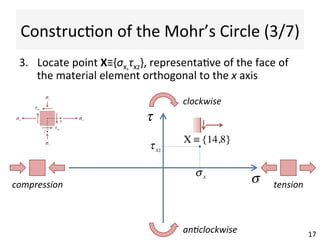
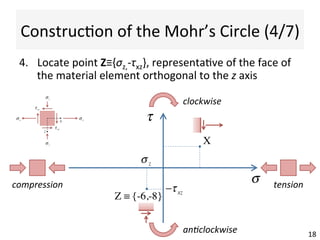
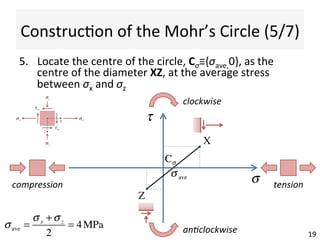
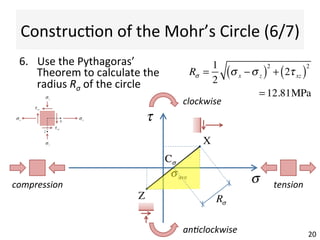
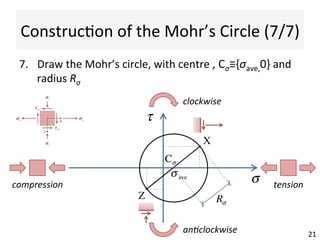
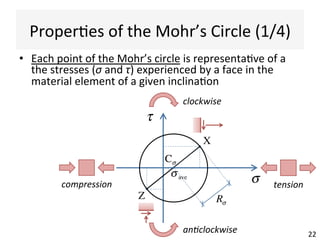
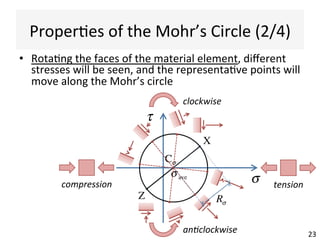
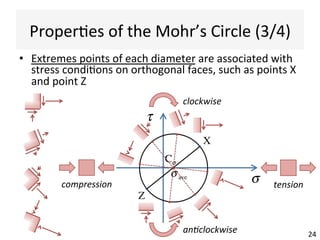
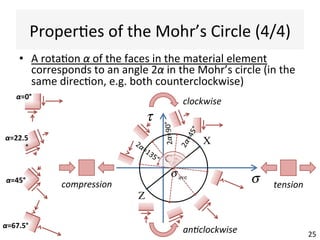
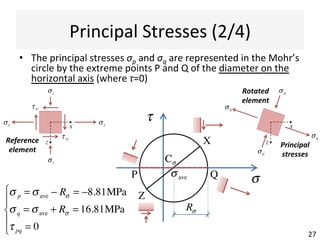
This document contains information about a teaching schedule for a course on complex stresses. It will cover topics like beam shear stresses, shear centres, virtual forces, compatibility methods, moment distribution methods, column stability, unsymmetric bending, and complex stress/strain over 11 weeks. The lectures and tutorials will be led by various staff members. The document also provides motivations for studying complex stresses, which include the fact that failure often results from different stresses acting together, and discussing examples like welded connections, reinforced concrete, and concrete cylinder tests.

1. Complex
Stresses
Dr
Alessandro
Palmeri
<A.Palmeri@lboro.ac.uk>

2. Teaching
schedule
Week Lecture 1 Staff Lecture 2 Staff Tutorial Staff
1 Beam Shear Stresses 1 A P Beam Shear Stresses 2 A P --- ---
2 Shear centres A P Basic Concepts J E-R Shear Centre A P
3 Principle of Virtual
forces
J E-R Indeterminate Structures J E-R Virtual Forces J E-R
4 The Compatibility
Method
J E-R Examples J E-R Virtual Forces J E-R
5 Examples J E-R Moment Distribution -
Basics
J E-R Comp. Method J E-R
6 The Hardy Cross
Method
J E-R Fixed End Moments J E-R Comp. Method J E-R
7 Examples J E-R Non Sway Frames J E-R Mom. Dist J E-R
8 Column Stability 1 A P Sway Frames J E-R Mom. Dist J E-R
9 Column Stability 2 A P Unsymmetric Bending 1 A P Colum Stability A P
10 Unsymmetric Bending 2 A P Complex Stress/Strain A P Unsymmetric
Bending
A P
11 Complex Stress/Strain A P Complex Stress/Strain A P Complex
Stress/Strain
A P
Christmas
Holiday
12 Revision
13
14 Exams
15
2

3. MoAvaAons
(1/5)
• Failure
of
structures
is
oJen
the
result
of
different
stresses
acAng
together
at
the
same
locaAon
• This
is
the
case,
for
instance,
of:
– Welded
connec)ons,
in
which
there
are
in
general
two
direct
stresses
to
consider
(σ
normal
and
σ
parallel
to
the
weld
axis)
and
two
shear
stresses
(τ
along
and
τ
normal
to
the
weld
axis)
3
Weld cross section. International Journal of Fatigue,
Volume 68, 2014, 178 - 185

4. MoAvaAons
(2/5)
– Reinforced
concrete
beams,
in
which
different
inclinaAons
of
the
cracks
appear,
depending
on
the
prevalent
shear
or
bending
acAon,
as
well
as
on
the
amount
and
distribuAon
of
reinforcement
4
RA=qL/2
RB=RA
B
q
A
L
V
M
prevalent
shear
force
V
prevalent
bending
moment
M

5. MoAvaAons
(3/5)
– Cracking
of
concrete
is
always
due
to
the
tensile
stress
σ
exceeding
the
tensile
strength
(fct)
of
the
material,
which
produces
a
rupture
(ideally
controlled
by
the
steel
reinforcement)
– However
this
means
that
the
orientaAon
of
the
tensile
stress
is
different
for
flexural
cracks
and
shear
cracks
5
– Also,
how
do
we
get
tensile
stresses
close
to
the
beam
supports,
where
the
prevalent
acAon
is
the
shear
force
V?
• And
we
know
(Zhuravskii’s
formula)
that
V
induces
τ,
not
σ
in
the
cross
secAon!
σ
>
fct

6. MoAvaAons
(4/5)
– Another
example:
While
tesAng
a
concrete
specimen
in
compression,
fricAon
sets
up
shear
stresses
at
the
base,
whose
effect
is
to
change
the
cracking
paern,
i.e.
the
direcAon
of
tensile
stresses
6
Damage
modes
observed
in
cylinder
compression
tests
as
a
funcAon
of
the
boundary
condiAons
Typical
hourglass
failure
mode
of
a
concrete
cylinder

7. MoAvaAons
(5/5)
– Cylinder
spli;ng
test
(also
known
as
‘Brazilian
test’)
is
used
to
determine
the
tensile
strength
of
concrete
– We
use
a
compression
force
(in
the
verAcal
direcAon)
to
set
up
tensile
stresses
in
the
horizontal
direcAon
(verAcal
fracture)…
How?
7

8. Learning
Outcomes
When
we
have
completed
this
unit
(2
lectures
+
1
tutorial),
you
should
be
able
to:
• Use
the
Mohr’s
circle
to
determine:
– principal
stresses,
and
their
direcAons;
– maximum
shear
stress,
and
the
inclinaAon
of
the
planes
where
it
occurs;
– normal
stress
and
shear
stress
in
any
inclined
plane
• Only
the
case
of
plane
stress
will
be
considered,
i.e.
no
out-­‐of-­‐plane
stresses
8

9. Further
reading
• R
C
Hibbeler,
“Mechanics
of
Materials”,
8th
Ed,
PrenAce
Hall
–
Chapter
9
on
“Stress
TransformaAon”
• T
H
G
Megson,
“Structural
and
Stress
Analysis”,
2nd
Ed,
Elsevier
–
Chapter
14
on
“Complex
Stress
and
Strain”
(eBook)
9

10. Stresses
in
Beams
and
Columns
(1/3)
Within
the
limits
of
the
Saint-­‐Venant’s
principle,
stresses
in
beams
and
columns
can
be
considered
to
be
in
plane
state:
10
The
difference
between
the
effects
of
two
different
but
sta6cally
equivalent
loads
becomes
very
small
at
sufficiently
large
distances
from
load
Adhémar
Jean
Claude
Barré
de
Saint-­‐Venant
(1797-­‐1886)
was
a
French
mechanician
and
mathemaAcian
• i.e.
normal
stresses
σ
(sigma)
and
shear
stresses
τ
(tau),
all
lie
in
the
same
plane

11. Stresses
in
Beams
and
Columns
(2/3)
11
Axial
(Normal)
Force,
N
Shear
Force,
V
Bending
Moment,
M
Twis)ng
Moment,
T
σ =
N
A
N N x
y
z
τ =
V ′Q
I b
V
y
z
σ =
M d
I
M
x
y
z
M
τ =
T r
J
T
y
z

12. Stresses
in
Beams
and
Columns
(3/3)
12
• There
oJen
situaAons
where
two
or
more
internal
forces
act
simultaneously
• In
a
curved
composite
bridge,
for
instance,
N,
V,
M
and
T
induce
complex
stresses
in
the
deck
secAon
• How
the
stresses
combine?

13. Plane
Stresses
(1/2)
13
• Let’s
consider
a
material
element
subjected
to
plane
stresses,
such
as…
– In
a
reinforced
concrete
shear
wall,
with
combined
compressive
and
lateral
forces
(e.g.
due
to
a
seismic
event)
V
P
xy
z
σz
τxz

14. Plane
Stresses
(2/2)
14
– In
the
the
web
and
in
the
flanges
of
a
thin-­‐walled
steel
cross
secAon
• Without
loss
of
generality,
the
plane
{x,z}
will
be
considered
in
our
analyses
x
y
z
τxz σ x

15. ConstrucAon
of
the
Mohr’s
Circle
(1/7)
1. The
values
of
the
three
stresses
σx,
σz
and
τxz
for
a
given
material
element
are
known
15
x
z
σxσx
σz
σz
τxz
τxz In
this
example:
• σx=
14
MPa
(tension)
• σz=
-­‐6
MPa
(compression)
• τxz=
8
MPa

16. ConstrucAon
of
the
Mohr’s
Circle
(2/7)
2. Draw
the
references
axes
in
the
Mohr’s
plane
– Normal
stresses
σ
in
the
horizontal
axis
• Posi2ve
if
in
tension
– Shear
stresses
τ
in
the
verAcal
axis
• Posi2ve
if
inducing
a
clockwise
rota2on
of
the
material
element
16
x
z
σxσx
σz
σz
τxz
τxz
σ
τ
tension
compression
clockwise
an2clockwise

17. σ
τ
tension'compression'
clockwise'
an0clockwise'
ConstrucAon
of
the
Mohr’s
Circle
(3/7)
3. Locate
point
X≡{σx,τxz},
representaAve
of
the
face
of
the
material
element
orthogonal
to
the
x
axis
17
x
z
σxσx
σz
σz
τxz
τxz
X ≡ {14,8}
σx
τxz

18. σ
τ
tension'compression'
clockwise'
an0clockwise'
ConstrucAon
of
the
Mohr’s
Circle
(4/7)
4. Locate
point
Z≡{σz,-­‐τxz},
representaAve
of
the
face
of
the
material
element
orthogonal
to
the
z
axis
18
x
z
σxσx
σz
σz
τxz
τxz
X
Z ≡ {-6,-8}
σz
−τxz

19. ConstrucAon
of
the
Mohr’s
Circle
(5/7)
5. Locate
the
centre
of
the
circle,
Cσ≡{σave,0},
as
the
centre
of
the
diameter
XZ,
at
the
average
stress
between
σx
and
σz
σ
τ
tension'compression'
clockwise'
an0clockwise'
Z
19
x
z
σxσx
σz
σz
τxz
τxz
X
Cσ
σave
σave =
σx +σz
2
= 4MPa

20. ConstrucAon
of
the
Mohr’s
Circle
(6/7)
6. Use
the
Pythagoras’
Theorem
to
calculate
the
radius
Rσ
of
the
circle
σ
τ
tension'compression'
clockwise'
an0clockwise'
Z
20
x
z
σxσx
σz
σz
τxz
τxz
X
Cσ
σave
Rσ =
1
2
σ x −σz( )2
+ 2τxz( )2
= 12.81MPa
`
Rσ

21. ConstrucAon
of
the
Mohr’s
Circle
(7/7)
7. Draw
the
Mohr’s
circle,
with
centre
,
Cσ≡{σave,0}
and
radius
Rσ
σ
τ
tension'compression'
clockwise'
an0clockwise'
Z
21
x
z
σxσx
σz
σz
τxz
τxz
X
Cσ
σave
Rσ

22. ProperAes
of
the
Mohr’s
Circle
(1/4)
• Each
point
of
the
Mohr’s
circle
is
representaAve
of
a
the
stresses
(σ
and
τ)
experienced
by
a
face
in
the
material
element
of
a
given
inclinaAon
σ
τ
tension'compression'
clockwise'
an0clockwise'
Z
X
Cσ
σave
Rσ
22
compression*

23. ProperAes
of
the
Mohr’s
Circle
(2/4)
• RotaAng
the
faces
of
the
material
element,
different
stresses
will
be
seen,
and
the
representaAve
points
will
move
along
the
Mohr’s
circle
σ
τ
tension'compression'
clockwise'
an0clockwise'
Z
X
Cσ
σave
23
compression*
Rσ

24. ProperAes
of
the
Mohr’s
Circle
(3/4)
• Extremes
points
of
each
diameter
are
associated
with
stress
condiAons
on
orthogonal
faces,
such
as
points
X
and
point
Z
σ
τ
tension'compression'
clockwise'
an0clockwise'
Cσ
σave
Z
X
24
compression*

25. ProperAes
of
the
Mohr’s
Circle
(4/4)
• A
rotaAon
α
of
the
faces
in
the
material
element
corresponds
to
an
angle
2α
in
the
Mohr’s
circle
(in
the
same
direcAon,
e.g.
both
counterclockwise)
σ
τ
tension'compression'
clockwise'
an0clockwise'
Cσ
σave
Z
X
25
compression*
α=0°
α=22.5
°
α=45°
2α=90°
α=67.5°

26. Principal
Stresses
(1/4)
• It
is
always
possible
to
find
two
orthogonal
faces
of
the
material
element
in
which
there
are
no
shear
stresses,
but
normal
stresses
only
σ
τ
tension'compression'
clockwise'
an0clockwise'
Cσ
σave
Z
X
26
compression*
• These
are
the
“principal
stresses”,
i.e.
maximum
and
minimum
values
of
the
normal
stress
for
the
varying
inclinaAon
of
the
element’s
face

27. Principal
Stresses
(2/4)
• The
principal
stresses
σp
and
σq
are
represented
in
the
Mohr’s
circle
by
the
extreme
points
P
and
Q
of
the
diameter
on
the
horizontal
axis
(where
τ=0)
σ
τ
tension'compression'
clockwise'
an0clockwise'
Cσ
σave
Z
X
27
P Q
σ p = σave − Rσ = −8.81MPa
σq = σave + Rσ = 16.81MPa
τ pq = 0
⎧
⎨
⎪
⎩
⎪
Rσ
x
z
σxσx
σz
σz
τxz
τxz
x
z
σq
σq
σ p
σ p
Reference
element
Rotated
element
Principal
stresses

28. Principal
Stresses
(3/4)
• The
principal
stresses
occur
along
the
principal
direcAons
of
the
stress,
p
and
q;
• They
are
orthogonal
each
other,
and
can
be
determined
considering
the
corresponding
angles
in
the
Mohr’s
circle
σ
τ
tension'compression'
clockwise'
an0clockwise'
Cσ
σave
Z
X
28
P Q
Rσ
x
z
σq
σq
σ p
σ pRotated
element
Principal
stresses
αxq = αzp = −
1
2
sin−1 τxz
Rσ
⎛
⎝⎜
⎞
⎠⎟
= −
38.6
2

= −19.3
αxq
2αxq
τxz
• Important:
It
is
assumed
here
that
angles
α
are
posi2ve
if
an2clockwise

29. Principal
Stresses
(4/4)
• In
case
of
brile
material,
such
as
concrete,
cracks
may
appear
orthogonally
to
the
direcAon
of
the
maximum
tensile
stresses
σ
τ
tension'compression'
clockwise'
an0clockwise'
Cσ
σave
Z
X
29
P Q
Rσ
x
z
σq
σq
σ p
σ pCracked
element
αxq
2αxq
τxz

30. Maximum
Shear
Stress
• The
maximum
value
of
the
shear
stress
is
τmax=Rσ
and
happens
in
two
mutually
orthogonally
faces,
which
are
inclined
by
45°
with
respect
to
the
principal
direcAons
of
the
stress
(represented
by
points
R
and
S
in
the
Mohr’s
circle)
σ
τ
tension'compression'
clockwise'
an0clockwise'
Z
X
30
P Q
τmax = Rσ
Cσ
σave
R
S
x
z
σave
σave
σave
σave
τmax
τmax

31. Stresses
on
an
Arbitrary
Inclined
Face
• Having
drawn
the
Mohr’s
circle,
it
is
possible
to
evaluate
the
normal
stress
σm
and
the
shear
stress
τmn
in
any
generic
face,
inclined
by
αxm
with
respect
to
the
horizontal
axis
σ
τ
tension'compression'
clockwise'
an0clockwise'
Z
X
31
P Q
Rσ
2αxq
τmn
Cσ
σave
M
N
σm
2αxm
σm = σave + Rσ cos 2αxm − 2αxq( )
τmn = Rσ sin 2αxm − 2αxq( )
⎧
⎨
⎪
⎩⎪
• Important:
It
is
assumed
here
that
angles
α
are
posi2ve
if
an2clockwise

32. Key
Learning
Points
1. Normal
stresses
and
shear
stresses
acAng
on
a
given
material
element
change
their
values
depending
on
the
inclinaAon
of
the
elementary
area
being
considered
2. The
Mohr’s
circle
allows
evaluaAng
– The
extreme
values
of
the
normal
stress
σp
and
σq
– The
extreme
value
of
the
shear
stress
τmax
– The
inclinaAon
of
the
faces
where
such
values
are
seen
– The
stresses
σm
and
τmn
for
an
arbitrary
inclinaAon
32