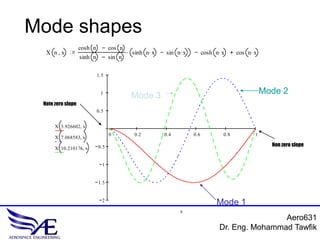
The document discusses the vibration of continuous structures, specifically focusing on strings, cables, bars, and beams. It covers the equations of motion, mode shapes, natural frequencies, and boundary conditions relevant to these structures, providing examples and homework problems for practical application. The content is structured to derive essential physics principles through analytical methods like separation of variables and eigenvalue problems.